负极性衰减振荡冲击电晕的数学物理模型

黄克捷　张小青　肖　翔（国家能源主动配电网技术研发中心（北京交通大学） 北京　100044）



负极性衰减振荡冲击电晕的数学物理模型

黄克捷张小青肖翔
（国家能源主动配电网技术研发中心（北京交通大学） 北京100044）

从气体放电微观物理过程出发，提出了一种负极性衰减振荡冲击电晕的数学物理模型，该模型考虑了碰撞电离、带电粒子迁移、空间光电离、电子与中性粒子的附着和带电粒子的复合。在已有文献的基础上，推导了同轴圆柱电极中的空间光电离公式。该模型可用来计算同轴圆柱电极中双指数冲击或衰减振荡冲击的负电晕伏库特性，计算结果与测量结果对比基本吻合。测量和计算结果表明，衰减振荡冲击下的伏库特性表现出明显的螺旋回环，这也是其与双指数冲击的主要区别。外施电压下降阶段，由于空间电荷的感应作用，内导体表面出现电场反向，有可能产生反极性电晕。利用提出的模型对反极性电晕过程中空间电场变化进行了定量分析。

衰减振荡冲击电晕模型空间光电离伏库特性反极性电晕

0　引言

雷电冲击波在沿架空线传播的过程中会发生衰减和变形，引起这种衰减变形的主要原因是线路上出现的冲击电晕。在雷电过电压的分析计算中，冲击电晕是一个需要考虑的主要因素，长期以来一直受到较广泛的关注［1］。一般来说，冲击电晕对雷电过电压的影响是通过其宏观外特性，即伏库特性来加以考虑的。现有的文献对双指数冲击波下的伏库特性已进行了大量研究，取得了较多成果［2-5］。事实上，由于波的折反射最终进入发电厂或变电站的雷电波往往不是标准的双指数冲击波，而是呈现出单极性衰减振荡特性［6］。同时，由于自然界中的雷电绝大多数为负极性，因此有必要对负极性衰减振荡冲击下的电晕特性进行建模研究。由于架空线附近的空间电场分布比较接近于同轴圆柱电极中内电极周围的电场分布，故可以使用同轴圆柱电极来研究架空线的电晕特性。

就目前已公布的文献来看，对于冲击电晕伏库特性模型的研究主要有3种方式:①通过假设一些宏观的边界条件来计算电晕放电的电荷与起晕导体电势之间的关系，这类方法通常不具体考虑放电的微观物理过程［7-9］；②从气体放电的微观物理过程出发，采用一些近似简化来模拟电晕放电中各种粒子在空间的运动过程［10，11］；③基于气体放电理论和电磁场理论，用数学方法对放电过程数学物理方程进行离散化求解［12］。

文献［8］基于起晕导体表面场强不会超过电晕起始场强以及放电边界场强不受外施电压影响这两点假设，提出了一个计算冲击电晕伏库特性的模型。该模型把空间电荷等效成一个面电荷，认为这个面电荷对空间合成电场的影响将满足以上两个假设，从而能够计算外施电压和空间电荷的关系。此方法不需要复杂的计算，便于工程上使用。但是此模型所基于的第一点假设，即起晕导体表面的场强不会超过电晕起始场强是来源于文献［13］的对交流电晕的测量结果，其测量时的采样间隔是250 μs，对于50 Hz交流电来说是足够的，但是却远大于雷电冲击的波头时间。此外，对于交流电晕来说每个周期的电晕放电有可能会受到前一个周期留在空间中的电荷的影响。因此，把交流电晕的测量结果直接应用到冲击电晕模拟中的做法在可行性上是值得商榷的。

文献［10］计算了同轴圆柱电极在正极性双指数冲击下的伏库特性，所提电晕模型将放电看做一代一代的电子崩，将空间电荷离散成围绕导体作圆柱分布的线电荷。该模型考虑了放电的微观物理过程，包括碰撞电离和空间光电离等，比较系统地描述了电晕放电的微观过程，但没有考虑负极性和衰减振荡冲击下的伏库特性。

文献［12］以电流连续性方程为基础计算了单根导体和分裂导线上的冲击电晕过程。其中运用了模拟电荷法（CSM）和有限元法（FEM）计算空间电场，随时间变化的迎风差分（TDUD）算法被用来计算空间电荷的迁移。由于在电晕放电过程中电荷与电场的关系非常紧密并互相影响，这将会给求解方程的数值算法提出较为苛刻的限制，同时，该文也没有涉及到衰减振荡冲击波。

本文提出一种新的冲击电晕模型，该模型能结合考虑电晕放电中的各微观物理过程（如碰撞电离、空间光电离、带电粒子的迁移、电子与中性粒子的附着、带电粒子的复合等），并能胜任衰减振荡冲击波下电晕伏库特性的计算。为了验证该模型的可能性，还采用同轴圆柱电极进行了实验测量，并将模型计算与实验测量结果进行了对比。

1　数学物理模型

1.1几点假设

电晕放电的微观物理过程复杂，为了简化建模计算，在充分考虑冲击电晕的主要微观物理过程情况下，本文拟做以下假设:

1）认为冲击电晕是电子崩发展而形成，后续电子崩是由空间中已经存在的电子崩产生的光子轰击内电极表面发射的光电子以及空间光电离释放的光电子引发的。

2）由于电极是圆柱对称的，初始电场也呈圆柱对称。认为电子崩朝圆柱径向均匀发展。假设电子崩头部的电子足够多，可以认为这些电子崩头部的电子是与内电极同轴的圆柱形电子层。忽略电子的扩散作用，则可认为该电子层是与内电极同轴的圆柱形面电荷。这样就可把每个电子层当作一个独立的对象来考虑，其属性包括电子层序号、空间位置和电子数量。放电过程中产生的正、负离子为与内电极同轴的圆柱形薄壳体电荷。在每个圆柱形薄壳内认为正、负离子均匀分布。

3）空间中的合成电场由外施电压和空间电荷共同决定。由于假定空间电荷与内电极呈圆柱对称分布，故可将带电粒子和电场的二维分布简化为沿内电极径向的一维分布。因此在对空间进行离散化的过程中，只需沿内电极径向做一维剖分，如图1所示，即将空间离散化为从内电极表面到外电极的厚度相同的圆柱形薄壳。这个假设主要是为了简化计算，同时文献［14］为这个假设提供了相应的实验依据。

图1　计算区域剖分示意图Fig.1　Subdivision schemes in calculation area

4）电子崩头部强烈的碰撞电离过程伴随着强烈的激励和反激励过程，忽略被激励粒子的寿命，认为引起光电离的光子主要是由电子崩头部的碰撞激励产生的。

5）在宇宙射线的作用下，空间中会存在微量自由电子，当内电极表面的电场强度达到电离的临界场强时，这些空间中的自由电子将作为首代电子崩的初始电子。文献［10］中提到的圆柱电极附近的初始电子数的计算公式为

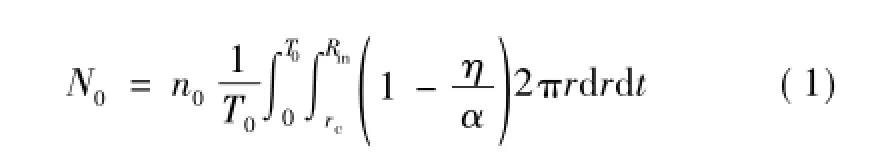
式中，n0为初始电子的体密度率，与外施电压的波头陡度有关［15］，μs-1·cm-3；T0为外施电压到达起晕电压U0［16］的时间，μs；rc为电离区边界半径，是时间t的函数，cm。

计算过程需要分别对时间和空间进行离散化处理，空间上的离散化已经在上文述及。由于电子漂移速度与电场有关，如果使用固定的时间步长将有可能在单个时间步长内电子行程超过一个空间步长，这样既会增加误差也会增加计算的难度。故在此借鉴文献［17］中的做法，令时间步长为该时刻速度最快的电子层通过一个空间步长的时间，即Δt=Δr/ve max。因此，本文提出的模型的时间步长是随时间变化的。

1.2离散化计算

假设在某一时刻t，已知上一个时间点t-Δt计算所得的空间电荷分布，计算过程如下。

1.2.1计算空间电场分布

由于外施电压为时间的已知函数，可以计算不计空间电荷时内、外导体单位长度上几何电容的充电电荷量（μC/m）

式中，u（t）为外施电压，kV；t为时间，ns；Cg为同轴圆柱电极单位长度的几何电容，nF/m，其表达式为

式中，ε0为真空介电常数，nF/m；Rin和 Rout分别为内、外电极半径，cm。

为了计算合成场强，还要考虑空间电荷的影响。首先计算每个圆柱薄壳中的净电荷量

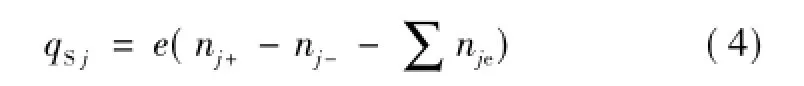
式中，nj+和nj-分别为正、负离子在第j个圆柱薄壳中的数量，下标j表示第j个圆柱薄壳，下标+、-分别表示正、负离子；∑nje为位于第j个圆柱薄壳内所有电子层电子数的总和；e为电子电荷量。

接着可由式（5）计算空间电荷在内电极上的感应电荷

式中，Aj为内电极电荷感应系数，其表达式为

由此，以rj为半径的单位长度圆柱面所包围的总电荷量可表示为

式中，N为离散化圆柱薄壳总数。当j=N时所求得的qj就是计算所得伏库特性中的q值。

求取qj后再由高斯定理可以计算rj处的场强

1.2.2计算带电粒子的漂移

已知空间电场的分布，由以下公式便可计算带电粒子的漂移速度［18］。

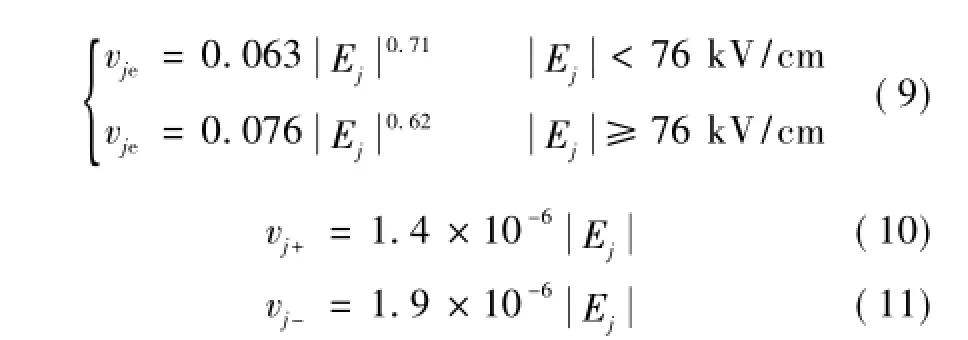
式中，vje、vj+、vj-分别为第j个圆柱薄壳中的电子、正、负离子漂移速度，cm/ns。

1.2.3计算碰撞电离、附着过程

计算出电子的漂移速度后就可确定该步的时间步长，进而计算各层电子在该时间步长内的漂移距离。对于正离子，由于假设在每个圆柱形薄壳内均匀分布，由式（12）可计算各薄壳中的电荷量。负离子同理。当带电粒子运动到电极表面时，将与电极上的异号电荷中和，这部分空间电荷消失。

式中，Vj为第j个圆柱薄壳的单位长度体积，cm3/m。

电子在沿电场方向漂移的过程中将获得能量，有可能产生碰撞电离，也有可能附着于中性粒子形成负离子。根据Townsend理论此过程可表示为

式中，nke为第k层电子的电子数；vke为第k层电子的漂移速度，cm/ns；αke和ηke分别为在vkeΔt距离内碰撞电离系数和附着系数的平均值，都是场强和气压之比（E/P）的函数［18］，cm-1。

若αke＞ηke，说明电离作用大于附着作用，电子数量增加，反之则说明附着作用大于电离作用，电子数量减少。由于对Δt的选取使得电子层在Δt内运动的最远距离不会超过一个空间间隔Δr，即电子层在Δt内将在一个圆柱体薄壳内运动或至多从一个圆柱薄壳运动到下一个圆柱薄壳。故在Δt内，第k层电子运动了vkeΔt距离后可认为形成的正、负离子留在该圆柱形薄壳内，其中正、负离子增加数可表示为

由于假设在每个圆柱形薄壳中正、负离子均匀分布，故可以把电离产生的正离子或附着产生的负离子直接累加到该薄壳内原有的正、负离子中。

1.2.4计算光电离过程

为了维持电晕放电的发展，需要有后续电子崩生成。对于负电晕来说，其来源主要有两个，即阴极上的光电子发射和空间中的光电离。

由于光电效应，内电极（在负电晕下表现为阴极）表面会发射出光电子，而这些光电子将作为从内电极发射的新电子层。光电子数是空间所有电子崩的光子在阴极表面所产生光电子数的总和。第k层电子所产生的光子在阴极表面释放的光电子数nkph为［19］

式中，γcathode为阴极上的光电子发射系数；μ为空间光吸收系数，cm-1；rke为第k层电子经Δt后距离阴极的距离，cm。

根据G.W.Penney在20世纪60年代所做的一系列实验研究［20-22］，空间光电离的强度与放电的强度呈正相关，即认为光子主要是由于电子崩头部伴随电离产生的激励和反激励产生的。同时最近的一些研究成果［23］也支持此结论，这就为空间光电离的模拟提供了可参考的依据。

文献［20］中建立的空间光电离模型是计算一个点电晕源在空间中另一个体积元中由光电离产生的光电子数，其数学表达式为［20］

式中，nR为在体积元QR内由于光电离所释放的光电子数；nD为光子来源点碰撞电离新产生的离子-电子对数；QR为光电离计算点体积元内气体分子数，QR=体积（cm3）×气压（mmHg）÷R2；A为常数，由测量数据求得，（cm×mmHg）-1；β为在1 mmHg情况下的空间光吸收系数，cm-1/mmHg；P为气压，mmHg；R为光子源到计算体积元QR的距离，cm。

由于本文假设空间中电子是呈圆柱状的面电荷，又因为对该圆柱对称系统只要空间中某一点的半径确定了，其所有的属性就能确定，故只需要把该模型从点对点拓展到面对点。如图2所示建立空间直角坐标系，令所求光电离的目标点为p点，坐标为（0，0，rc），光子发射的源为半径为rke圆柱上的任意一面积元dS，坐标为（x，y，z）。R为dS和p之间的距离。则由式（16）可推出dS处发射出的光子在p点体积元内产生的光电子数为

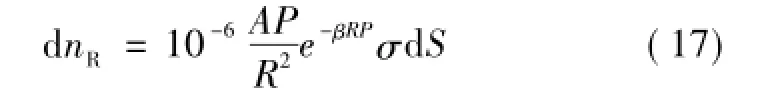
式中，σ为dS处由碰撞电离产生的离子-电子对的面密度，可表示为

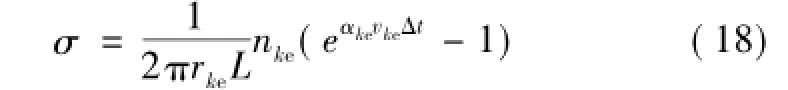
图2　空间光电离推导过程Fig.2　Space photoionization derivation process

显然由于内电极的存在，空间中只有一部分光子能够到达p点，其余的光子会被内电极挡住。事实上，能够到达p点的光子范围是可计算的，此范围和Rin、rke、rc的值有关。但为了简化计算，同时从式（16）可看出，光电离效应随着R的增大呈指数衰减，故计算中只计及点p所在的上半圆柱的影响，如图2所示。当Rin、rke、rc的值在同一个量级时此简化是可以接受的。因此对式（17）进行积分便可求得光源所在圆柱面在p点由光电离释放的单位体积电子数。注意到式（17）是个曲面积分，积分区域是半径为rke的上半圆柱，易知该曲面表达式为

这样就可将曲面积分化为二重积分

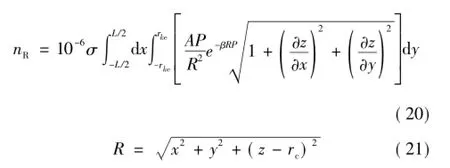
式中，L为圆柱轴向长度，即电极轴向长度，cm；R 为dS到p点距离，cm。

此积分可由数值积分的方法求解，求解过程中发现，当L取1 cm时该积分已经趋于收敛。由于1 cm远小于实际电极长度，故可忽略电极两端的边缘效应。

空间光电离计算过程如图3所示，其中Rin为内电极半径，rke为当前计算电子层经Δt后移动到的位置，rk和rj分别是该电子层所在剖分的相邻剖分，rc为电离区边界（α=η）。当计算第k层电子碰撞电离的同时就可以计算rc内所有剖分上由于该电子层而产生的光电子。若某个剖分中已经存在电子层，则可将光电子加入到该电子层中去，以减少计算量。在所有由于光电离新生成的电子层中，最重要的是在内导体表面及电离区边界的光电子层，因为它们将作为后继电子引发新的电子崩。由于空间光电离释放的光电子很少，对空间电场影响可以忽略，故电离区以外没有必要进行计算。

图3　空间光电离示意图Fig.3　Schematic diagram of space photoionization

1.2.5计算正、负离子的复合

对于正、负离子，按照式（22）计算Δt内由于复合而引起的电荷量减少［18］。

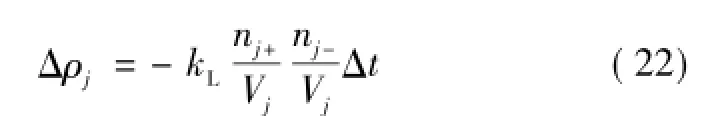
式中，kL为复合系数，cm3/ns；Δρj为第j个圆柱薄壳内的正、负离子密度的变化量，cm-3。

以上的计算模型通过Matlab编程实现，模型的整个离散化计算过程的流程如图4所示。

图4　模型计算过程流程Fig.4　Flowchart of the computation process

2　计算参数选择

以上建立的模型将用来计算一个同轴圆柱电晕笼在衰减振荡冲击波下的伏库特性，其中电晕笼的内电极的半径为0.1 cm，外电极的半径为50 cm，空间离散步长Δr取0.01 cm，电离系数α和附着系数η取在干燥空气中的测量结果［24］。由文献［18］，光电子发射系数 γcathode取 7.6×10-4，空间光吸收系数 μ取6 cm-1。光在1 mmHg气压下空气中的吸收系数β取0.017 6 cm-1［22］，而常数A取25.7［20］。气压取一个标准大气压。求解数值积分式（20）时取绝对误差限10-10。复合系数 kL取 1.4×10-6cm3/s［18］。外施电压u（t）为由实测数据拟合得到的函数。由文献［24］的测量结果，在一个大气压下空气中的临界场强Ecr= 24.4 kV/cm（即α=η）。

3　计算和测量结果

为了验证本文提出的电晕模型，在高压实验室中采用电晕笼进行了相应的实验，实验布置如图5所示。电晕笼为一同轴圆柱电极系统，外电极是由镀锌铁皮卷制的圆筒，其轴向长度L=1 m，内电极为一根圆柱形铜条。为了抑制边缘效应，在主电极两端设置两个屏蔽电极，轴向长度为0.5 m。衰减振荡波冲击电压是通过在传统冲击电压发生器波头电阻位置串入高压电感线圈产生的，如图6所示。它由一条垂直于内电极的铜带施加在内电极上以产生电晕放电。外施电压信号u通过电容分压器引出，电晕电荷信号q通过在外电极与地之间的积分电容Cq引出。引出的信号经过二次分压接入屏蔽室中的数字示波器，通过消去时间t就可获得伏库特性曲线。

图5　实验布置示意图Fig.5　Schematic diagram of the experiment setup

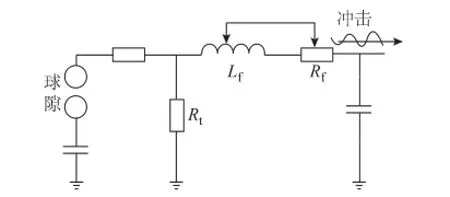
图6　衰减振荡冲击发生器Fig.6　Damped oscillisatory impulse generator

实验中外施电压波形如图7a所示，对于双指数波参数为0.95/50 μs，幅值-200 kV，衰减振荡波幅值为-200 kV，频率为0.42 MHz。对应的实测伏库特性见图7b。将图7a所示电压经拟合后输入本文所建立的电晕模型，所得到的计算伏库特性如图7c所示。从图7b、图7c中可知，对于双指数波测量结果和计算结果基本一致（由于双指数波波尾下降很慢，计算完整个波尾需要很长时间，故只计算到-50 kV）。为了进一步验证模型的正确性，保持外施电压的幅值不变，改变振荡频率为0.17 MHz，相应的测量和计算结果如图8所示。通过对比图7b、图7c以及图8b、图8c可见，对于不同频率下衰减振荡波测量结果和计算结果在趋势上也能基本吻合。这就说明本文建立的电晕模型能在很大程度上刻画冲击电晕的放电行为，既能模拟双指数波又能模拟衰减振荡波，适用于不同波形的外施电压，通用性较好。

图7　负极性双指数、衰减振荡冲击下伏库特性Fig.7　q-u curves under nagetive double exponential and damped oscillatory impulses

图8　改变振荡频率后负极性衰减振荡冲击下伏库特性Fig.8　q-u curves under nagetive damped oscillatory impulses with a changed frequecy

外施电压达到第一个波峰之后便开始下降。由于电压下降电场也必然衰减，通常认为在此阶段放电停止，在伏库特性中该段下降曲线应是一条斜率等于几何电容值的线段［10］。但是分析图7b可以发现，实测中该曲线下降的斜率要大于几何电容值，说明该阶段存在影响空间电荷分布的某些过程，造成空间电荷的数量或位置发生变化。同时，由图7和图8可见，衰减振荡波下电晕伏库特性主要特征是其特性曲线呈现出明显的螺旋回线特征。这是它与传统双指数冲击波下电晕伏库特性的主要区别。引起这种特征的主要原因可能是在外施电压的振荡过程中所产生的反极性电晕［6，7，9］。从电荷的角度来看，对于负极性的冲击电晕，由于电离基本发生在紧邻内导体的区域，而电子是逐步被气体分子俘获变成负离子，故空间中正离子相对集中而负离子相对分散。与此同时，正离子在电场的作用下向内电极缓慢迁移，会有一部分正离子被内电极吸收，空间的净电荷将为负极性（即与外施电压同极性）。因此空间电荷在内导体上的感应电荷为正极性（即与外施电压反极性）。显然，对于负极性的外施电压，内导体上因其产生的充电电荷为负极性。故随着外施电压的下降，内导体上的充电电荷会减少，一旦充电电荷少于感应电荷，内导体上的总电荷（充电电荷+感应电荷）将表现出与外施电压相反的极性。由高斯定理可知，内导体表面的电场将会发生反向。如果外施电压进一步降低，反向的电场将会随之增强，有可能会超过临界场强。这就为反极性电晕的发生创造了条件。

一旦发生反极性电晕，空间中正离子数量增加，则相对应地在内电极上将感应出更多的负电荷。内导体上的总电荷可能重新变为负极性，导体表面场强将再次反向。若此时反极性电晕仍在发展，由于此时导体表面场强已反向，电子将难以到达内导体，其将在内导体附近被中性粒子俘获变为负离子。因此空间电荷会呈现出分层的现象，此种电荷分层现象在文献［7］中也有提及。如果外施电压反复衰减振荡，此过程将重复出现，这样空间中的电荷将呈现出多层。在本文的计算中发现，在图7a所示外施电压的第一个下降阶段，空间电荷出现了分层现象。

图9是对应图7衰减振荡波的计算过程中1.60 μs、1.70 μs和1.80 μs三个时刻内电极附近电场随距离变化曲线，其中设电场正方向为径向向外。从图9可见1.60 μs时电场开始反转，在1.70 μs时反转电场已经超过临界场强Ecr具备反极性电晕发展的条件，1.80 μs时由于反极性电晕的作用，导体表面电场开始呈下降趋势。从对应的伏库特性曲线中也可看出，约1.70 μs后电荷量开始加速下降。

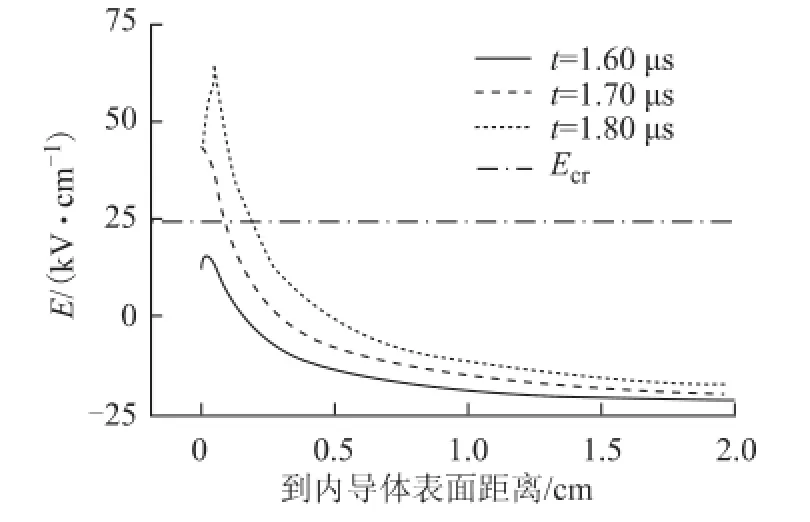
图9　反极性电晕发展过程中空间电场分布Fig.9　Space electric field distribution during the development of opposite polarity corona

4　结论

本文提出了一种负极性衰减振荡冲击电晕的物理数学模型，推导了同轴圆柱电极中空间光电离公式。该模型基于气体放电的物理过程，能考虑碰撞电离、带电粒子漂移、空间光电离、电子与中性粒子的附着和带电粒子的复合等微观物理过程。运用该模型既能计算传统的双指数雷电波又能计算衰减振荡波的伏库特性，具有较好的适应性。

由该模型计算的伏库特性与实验测量结果能较好地吻合，验证了该模型的可靠性。实验和计算结果均表明，衰减振荡波下的伏库特性表现出明显的螺旋回线特征，这是其与传统双指数冲击波下伏库特性单调回线的主要区别。同时，模型计算还表明，在外施电压衰减振荡过程中，当外施电压下降到一定程度时，内导体附近可能产生反极性电晕，从而令相应的电晕伏库特性产生次回环。

［1］卢毓欣，韩永霞，朱志芳，等.±1 000 kV特高压直流换流站绝缘配合［J］.电工技术学报，2014，29（增1）:516-523.

Lu Yuxin，Han Yongxia，Zhu Zhifang，et al.The insulation and coordination of±1 000 kV UHVDC converterstation［J］.TransactionsofChina Electrotechnical Society，2014，29（S1）:516-523.

［2］胡琴，吴执，舒立春，等.交流电场下水滴对导线电晕特性的影响［J］.电工技术学报，2015，30 （18）:237-245.

Hu Qin，Wu Zhi，Shu Lichun，et al.The corona characteristics of the conductor attached with water drops under AC electrical Field［J］.Transactions of China Electrotechnical Society，2015，30（18）:237-245.

［3］廖瑞金，伍飞飞，刘康淋，等.棒-板电极直流负电晕放电脉冲过程中的电子特性研究［J］.电工技术学报，2015，30（10）:319-329.

Liao Ruijin，Wu Feifei，Liu Kanglin，et al.Simulation of characteristics of electrons during a pulse cycle in barplate DC negative corona discharge［J］.Transactions of ChinaElectrotechnicalSociety， 2015， 30（10）: 319-329.

［4］刘阳，崔翔，卢铁兵，等.湿度对绞线正极性电晕电流脉冲及其无线电干扰影响的实验［J］.电工技术学报，2015，30（3）:79-89.

Liu Yang，Cui Xiang，Lu Tiebing，et al.Experimental investigation ofhumidityimpactonpositivecorona current pulse and its radio interference of stranded conductors［J］.Transactions of China Electrotechnical Society，2015，30（3）:79-89.

［5］张满，蒋兴良，舒立春，等.混合凇对分裂导线起晕电压影响［J］.电工技术学报，2015，30（3）: 258-267.

Zhang Man，Jiang Xingliang，Shu Lichun，et al.The influences of mixed-phase ice on corona inception voltage ofbundleconductor［J］.TransactionsofChina Electrotechnical Society，2015，30（3）:258-267.

［6］张小青，吴维韩，黄炜纲.冲击电晕特性的计算模型［J］.清华大学学报（自然科学版），1992，32 （4）:72-78.

Zhang Xiaoqing，WuWeihan，HuangWeigang.A computational model of impulse corona characteristics ［J］.Journal of Tsinghua University（Science and Technology），1992，32（4）:72-78.

［7］Semlyca A，Huang W G.Corona modelling for the calculation of transients on transmission lines［J］.IEEE Transactions on Power Delivery，1986，1（3）:228-239.

［8］Al-Tai M A，Elayyan H S B，German D M，et al.The simulation of surge corona on transmission lines［J］. IEEE Transactions on Power Delivery，1989，4（2）: 1360-1368.

［9］Cooray V.Charge and voltage characteristics of corona discharges in a coaxial geometry［J］.IEEE Transactions on Dielectrics and Electrical Insulation，2000，7（6）: 734-743.

［10］Abdel-Salam M，Stanek E K.Mathematical-physical model of corona from surges on high-voltage lines［J］. IEEE Transactions on Industry Applications，1987，IA-23（3）:481-489.

［11］Sheng Caiwang，Zhang Xiaoqing.Modeling of corona underpositivelightningsurges［J］.Journalof Electrostatics，2013，71（5）:848-853.

［12］ LiWei，ZhangBo，ZengRong，etal.Dynamic simulation of surge corona with time-dependent upwind difference method［J］.IEEE Transactions on Magnetics，2010，46（8）:3109-3112.

［13］Waters R T，Rickard T E S，Stark W B.Direct measurement of electric field at line conductors during a.c.corona［J］.ProceedingsoftheInstitutionof Electrical Engineers，1972，119（6）:717-723.

［14］Hermosillo V F，Cooray V.Space-charge generation and neutralisation in a coaxial cylindrical configuration in air underanegativevoltageimpulse［J］.Journalof Electrostatics，1996，37（3）:139-149.

［15］Mayo B.Surgesinhigh-voltagenetworks［J］.IEE Review，1981，27（3）:249.

［16］Peek F W.Dielectric phenomena in HV engineering ［M］.New York:McGraw-Hill，1929.

［17］KlineLE.Calculationsofdischargeinitiationin overvolted parallel-plane gaps［J］.Journal of Applied Physics，1974，45（5）:2046-54.

［18］杨津基.气体放电［M］.北京:科学出版社，1983.

［19］Nasser E.Fundamentals of gaseous ionization and plasma electronics［M］.New York:Wiley-Interscience，1971.

［20］Penney G W.Photoionization measurements in air，oxygen，and nitrogen［J］.Journal of Applied Physics，1970，41（2）:572.

［21］Penney G W，Voshall E R.Ionization of a gas by radiation from a discharge［J］.American Institute of ElectricalEngineers，PartI:Transactionsofthe Communication and Electronics，1963，81（6）:398-403.

［22］Penney G W，Nygren S F，Voshall R E.Photoionization as the secondary mechanism in a Townsend breakdown ［J］.IEEETransactionsonCommunicationand Electronics，1964，83（71）:203-208.

［23］Nijdam S，De Wetering F，Blanc R，et al.Probing photo-ionization:experiments on positive streamers in pure gases and mixtures［J］.Journal of Physics D: Applied Physics，2010，43（14）:145204.

［24］Harrison M A，Geballe R.Simultaneous measurement of ionizationandattachmentcoefficients［J］.Physical Review，1953，91（1）:1-7.

黄克捷男，1989年生，博士研究生，研究方向为过电压保护与防雷。

E-mai:13117380@bjtu.edu.cn（通信作者）

张小青男，1957年生，教授，博导，研究方向为过电压保护与防雷。

E-mai:zxqing002@163.com

Mathematical Physical Model of the Corona Under Negative Damped Oscillatory Impulse

Huang KejieZhang XiaoqingXiao Xiang
（National Active Distribution Network Technology Research Center Beijing Jiaotong UniversityBeijing100044China）

Based on the microcosmic physical processes of gas discharge，a mathematical physical model of the corona under negative damped oscillatory impulse is proposed in this paper.Collision ionization，drift，space photoionization，attachment and recombination are included in the proposed model.The space photoionization formula is deduced in a coaxial cylindrical geometry.The charge-voltage characteristics under the negative damped oscillatory or the double exponential impulses can be computed by the proposed model.The computed results can agree reasonably with those observed from experimental measurement.Both measurement and computation show that helical trajectories appear on the charge-voltage curves under damped oscillatory impulses，which reveals the main difference between the damped oscillatory and the double exponential impulses.In the decreasing range ofthe applied voltage，the electric field near the inner conductor is found to undergo a reversal due to the induction of space charge.As a result，the opposite polarity corona may occur.Using the proposed model，quantitative analysis is carried out for the electric field in the development process of the opposite polarity corona.

Dampedoscillatoryimpulse， coronamodel， spacephotoionization， charge-voltage characteristic，opposite polarity corona

TM851

2015-05-09改稿日期 2015-08-27