Al基非晶合金表征参数的支持向量回归分析

徐 燕，张玉凤，高 湉，张 研，张惠然，刘永生（. 上海电力学院 数理学院，上海 0399；. 上海大学 计算机工程与科学学院，上海 00444）

Al基非晶合金表征参数的支持向量回归分析

徐 燕1，张玉凤1，高 湉1，张 研2，张惠然2，刘永生1
（1. 上海电力学院 数理学院，上海 201399；2. 上海大学 计算机工程与科学学院，上海 200444）

根据一系列 Al基非晶合金薄带实测数据集，应用粒子群优化支持向量回归方法（PSO-SVR），建立一个通过相关表征参数来预测Al基非晶合金晶化温度（Tx）的模型。利用该模型对不同类型铝基非晶合金的晶化温度（Tx）进行建模和预测研究，并与反向传播神经网络（BPNN）预测方法进行比较。结果表明：基于留一交叉验证法（LOOCV）的PSO-SVR模型预测的晶化温度误差要比BPNN模型预测的小得多，这说明模型中所采用的特征参数能很好地描述该系列Al基非晶合金的晶化行为和热稳定性。

Al基非晶合金；晶化温度；支持向量回归；粒子群优化

非晶合金，俗称“金属玻璃”，与金属相比具有长程无序、短程有序的结构，因而具有独特而优异的物理、化学及力学性能，使其极具生产应用的优势。其中，Al 基非晶合金是一种高强度低密度的材料，且Al 基非晶纳米晶复合材料的比强度与工程陶瓷的接近，具有很大的应用潜力［1−3］。这使得近年来快速发展的 航空航天以及交通工具的轻型化的需求得以满足。但在晶化过程中金属间化合物的析出会导致复合材料的强度降低，还会使材料由韧变脆［4］，因此，Al基非晶合金的晶化行为值得深入研究［5］，找出晶化温度与其它相关表征参数之间的关系也很有意义。

LISBOA等［6］提出将Al基合金分为纳米晶合金、纳米玻璃合金、玻璃合金3大类，并且利用拓扑不稳定参数λ来说明晶化初生相与合金类型之间的关系。拓扑不稳定参数λ的核心思想是当溶质原子和溶剂原子的体积错配达到一定程度时，由此引起的应力将导致晶体结构的失稳，最终形成非晶［7］。然而，即使是同一体系的合金，也很难有确定的λ值将3种类型的合金分类［8］。

除了拓扑不稳定参数 λ，研究者也试图通过其他一些参数来说明相关关系。ZHANG等［9］提出可以用体系电负性的偏差Δe值来确定Al基非晶合金的类型。JIA等［10］提出了一个准等价团簇模型（Al5TM）x-（Al10RE）y，即对于TM和RE摩尔分数分别为x和y 的 Al100−x−yTMxREy合金，参数（6x+11y）可以预判Al-TM-RE非晶合金的类型。与λ一样，很难找到一个临界 Δe和（6x+11y）来区分合金的晶化类型［11］。同时，在同一Al-TM-RE系中合金组元间的化学混合焓ΔHmix直接反应了异类原子之间相互作用的强弱以及混乱程度，以往许多工作业已表明Tx与ΔHmix存在较好的线性关系［11−12］。但是，对不同体系的 Al-TM-RE非晶合金而言，区分其合金类型的临界 λ′以及ΔHmix值并不是固定的，而是随RE原子的半径和电负性的变化而变化。

对于Al基非晶合金中如此复杂的表征参数，数据挖掘可从大量的、存在噪声的、冗余的和缺损的数据中提取蕴藏其中有用的知识。目前，关于Al基非晶合金晶化行为和热稳定性的研究，还只是简单地通过图表法去分析它们之间的相关性［11］。统计分析只能研究同一体系中这些参数与晶化温度之间的关系，而无法根据这些特征参数去预测Tx值。而在不同Al-TM-RE系的研究中，统计方法却不能得到很好的结论。机器学习方法［13］可以研究不同体系中相关特征参数与 Tx之间的关系，而前人在 Al基费劲合金的研究中则很少使用这种方法方法。本文作者则是将 PSO-SVR方法与Al基非晶合金热稳定性研究相结合，通过特征参数λ、Δe、（6x+11y）、∆Hmix、λ′等来预测Tx值，为进一步实验提供理论指导，减少实验的盲目性。

1 原理与方法

1.1 PSO-SVR方法

20世纪90年代，VAPNIK［14］在求解分类问题时候提出了支持向量机（Support vector machine，简称SVM）理论，它以统计学习理论中的VC维理论和结构风险最小原理为基础，利用有限的样本信息在模型的复杂性（对特定训练样本的分类精度）和学习能力（无错误地识别任意样本的能力）之间寻求最佳折衷，以获得最好的分类性能和推广能力。经过不断发展，SVM已经在解决实际问题中得到了广泛应用［15−17］。与其他机器学习方法如遗传算法人工神经网络等方法相比，SVM具有更好的学习能力和泛化能力，因而引起了人们对这一领域的极大关注。支持向量回归（SVR）是SVM的一种延伸，可以有效地完成非线性拟合［14， 18−19］。针对不满足线性关系的样本集（x1， y1），…，（xm， ym），通过输入空间到输出空间的非线性映射Φ，将样本集中的数据x映射到高维空间F，并在特征空间F中用下述函数）（xf进行线性回归：

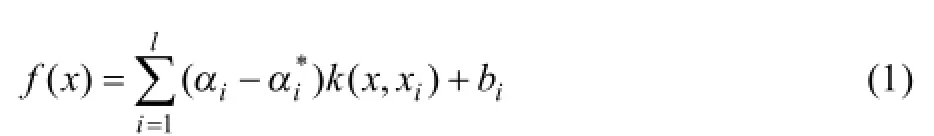
式中：l为训练样本个数；αi和是拉格朗日乘子；k（x，xi）=Φ（x）·Φ（xi）是一个核函数；b是阈值。本文作者采用径向基核函数，SVR的详细原理可以参考［14］。

粒子群优化算法（Particle swarm optimization， PSO）是一种进化计算技术（Evolutionary computation），它是由Kennedy博士和Eberhart教授于1995提出的［20］，其设想是模拟鸟群觅食的过程，每个优化问题的解都是搜索空间中的一只鸟，即所谓的粒子。所有的粒子都有一个由被优化的函数决定的适应值，每个粒子还有一个速度以决定它们飞翔的方向和距离，然后粒子们就跟踪当前的最优粒子在解空间中的搜索。粒子在搜索的过程中会不断地用当前个体值和全局极值来更新自己，直到找到全局最优解为止。PSO是一个很好的参数优化工具，在本实验中，PSO被用来寻找 SVR的最优参数（C， γ）。根均方差（Er）作为适应度函数：

式中：m为训练样本数；iy和yˆ分别表示训练样本的实验测量值和预测值。

1.2 泛化性能评估

两个指标，也就是平均绝对误差（Ema）和平均相对误差（Emap）被用来作为泛化性能评估。它们的公式如下：

2 预测模型的建立

本实验中所用实验数据集源自文献［11］。该数据集总共有66个数据样本，包含晶化温度Tx，化学混合焓∆Hmix、拓扑不稳定参数 λ、电负性差∆x、参数（6x+11y）以及用有效原子半径修正后的拓扑不稳定参数λ′等6维数据向量。相关数据如表1所列。

张章等［11］指出，非晶合金的晶化过程需要进行原子的扩散，影响非晶合金热稳定性的主要因素来自两个方面：电负性和原子尺寸。电负性的大小能反映化学键的强弱和混合热的大小，而溶剂原子与溶质原子尺寸大小也能影响热稳定好坏，因此非晶晶化温度 Tx与其组元密切相关。统计结果表明：同一Al-Ni-RE系非晶合金的λ′、∆Hmix等参数的两个临界值可以将其分为纳米晶、纳米玻璃、玻璃合金三类［8］。然而，对于不同体系的Al-Ni-RE非晶合金，却不再有明显的临界值。同时，统计方法无法通过这些特征参数来计算得出一个确定的 Tx值，而只能得到一些相关的线性关系。机器学习方法却可以使用训练样本训练一个模型，然后通过该模型预测得到一个在一定精度范围内的Tx值，这就很好地解决了统计学习方法无法解决的问题。

在使用实验中所提到的预测方法训练和建模过程中，以化学混合焓∆Hmix、拓扑不稳定参数λ、电负性差∆x、参数（6x+11y）以及用有效原子半径修正后的拓扑不稳定参数λ′等五维数据向量为输入变量，以Tx为输出向量进行训练学习。首先，这66条样本数据要进行规范化处理，未经预处理的样本数据各维特征差异较大，若直接用于机器学习方法，将会极大地影响其预测准确率。在本实验中，使用简单的数据归一化方法进行处理，之后，给定的样本数据集被分为两类：训练集和测试集。这66条样本数据被BPNN方法和PSO-SVR方法进行训练建模，调整模型的正确性以及预测处理。本文作者使用留一交叉验证法（LOOCV）［21］划分数据集，即使用其中65条数据为训练集，剩下的一条数据为测试集，并且这 66条数据逐一作为测试集。一旦预测模型训练完成，测试集将会用来评估这个预测模型。测试集作为这个已完成训练的预测模型的输入，得到的结果将被计算该模型的预测精度以及泛化能力。

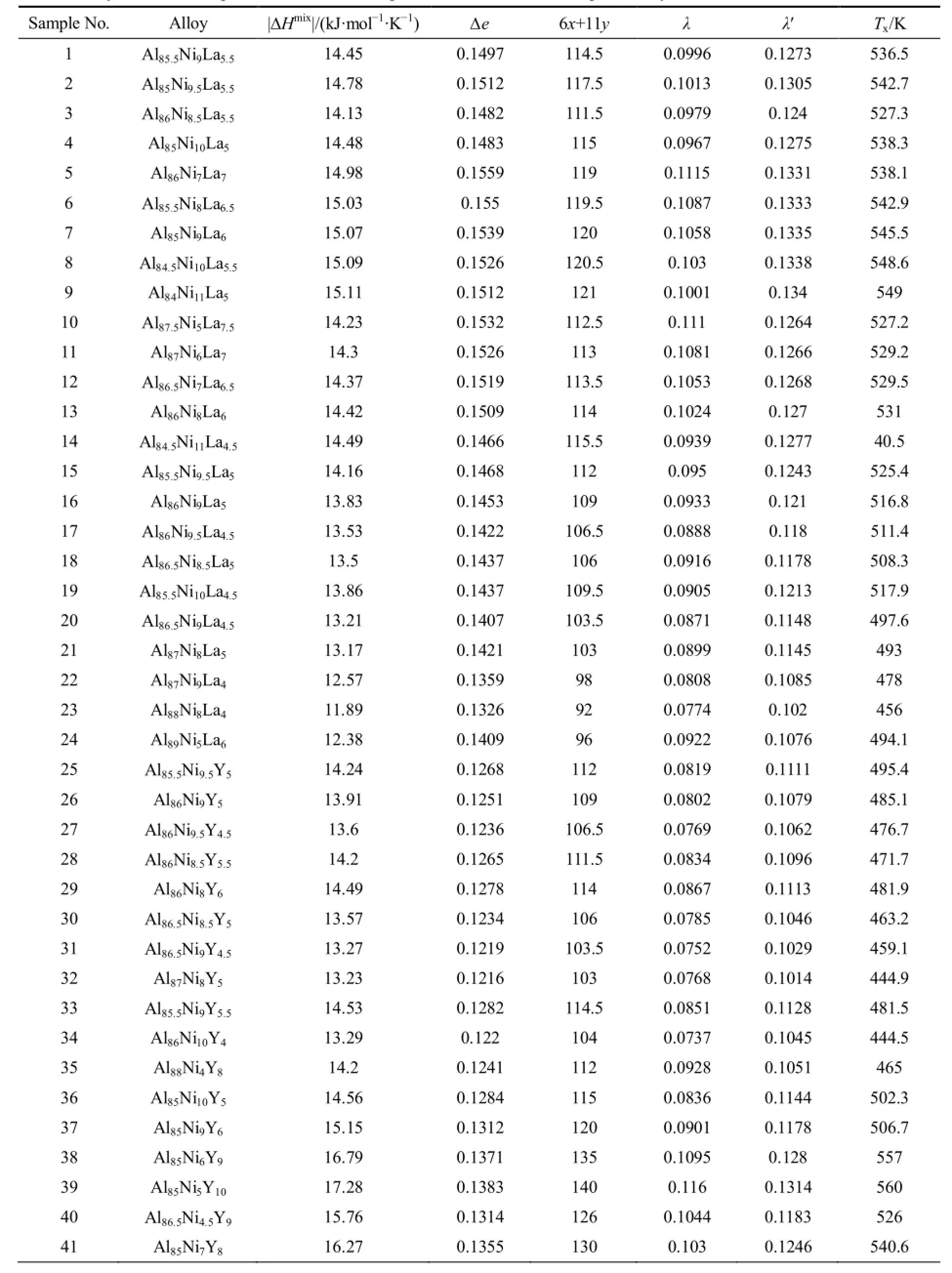
表1 Al基非晶晶化温度和相关参数［11］Table 1 Crystallization temperature Txand relevant parameters of Al-based amorphous alloys［11］

续表1

3 结果与分析

表2所示为使用BPNN及基于LOOCV的PSO-SVR两种回归方法对Al基非晶合金Tx进行预测所得的计算结果和误差。

从表2中可以看出，在PSO-SVR预测的66个样本中，所有样本的绝对误差都小于4.2%。其中，绝大多数样本（52/66=78.8%）的绝对误差小于2%。而BPNN模型的计算结果中，只有 56.1%（37/66）样本的绝对误差小于2%，且最大误差高达13.4%。在横向比较中，采用PSO-SVR方法时56.1%（37/66）的样本预测误差比BPNN方法预测的要小。该结果表明：在大多数样本中，PSO-SVR方法比BPNN方法具有更好的预测精度。

图 1所示为 Al基非晶合金 Tx实测值和通过PSO-SVR方法以及BPNN方法得到的预测值的对比。从图1可以直观地看出，绝大多数样本的PSO-SVR预测值都落在最优拟合线上或线的附近，比 BPNN方法的预测值更接近实测值。且与实测值相比，BPNN模型的计算误差普遍明显偏高。这些结果再次表明：与BPNN方法相比，PSO-SVR方法预测结果更接近实测值，且具有更高的预测精度以及更好的泛化能力。

表2 Al基非晶Tx测量结果与BPNN和基于LOOCV的PSO-SVR预测结果的对比Table 2 Comparison between experimental and predicted values of Txby using BPNN and PSO-SVR methods

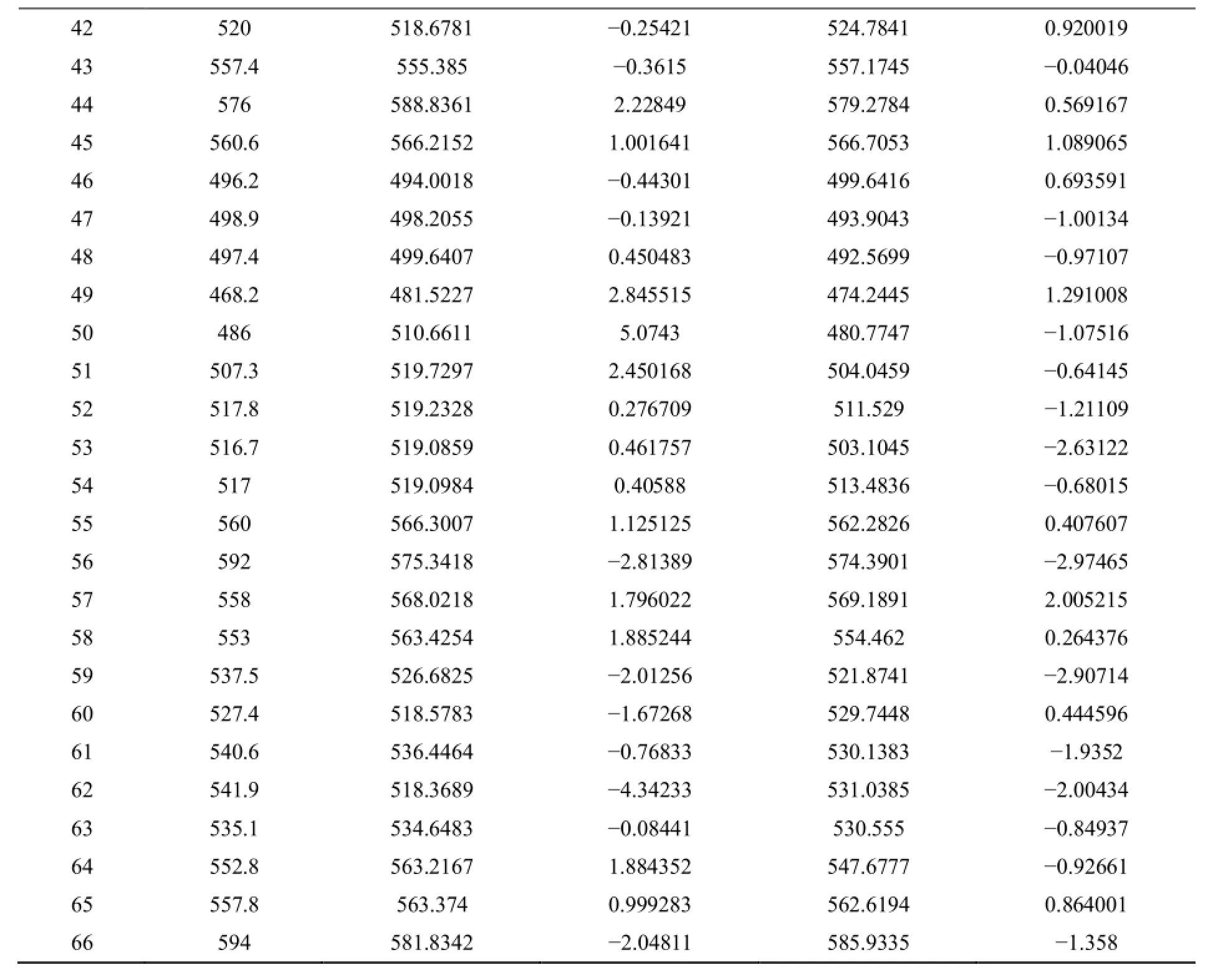
续表2

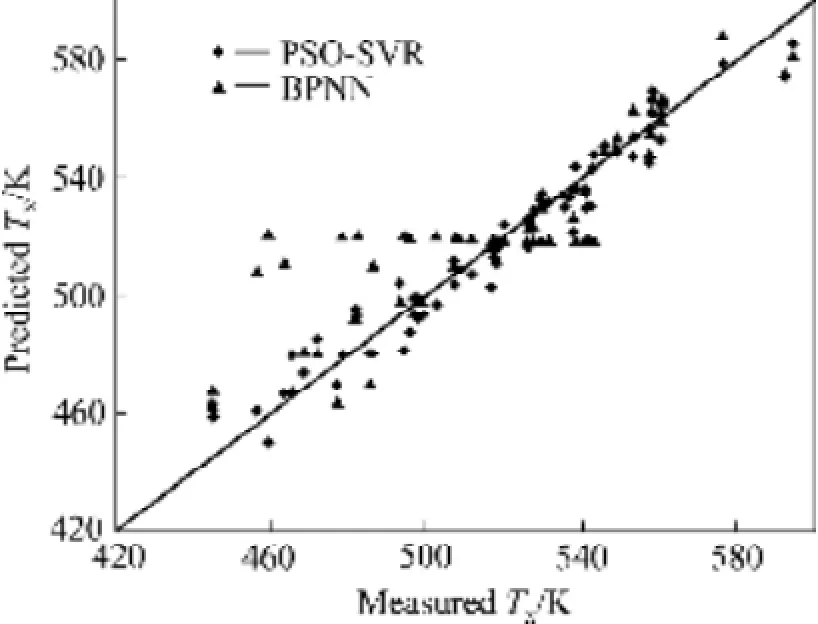
图1 通过PSO-SVR和BPNN得到的预测值与实测值对比图Fig. 1 Comparison of experimental values vs predicted values by BPNN and PSO-SVR

表3列出了使用BPNN和PSO-SVR两种方法得到的评价指标值。从表3可以看出，PSO-SVR预测结果的Er（7.6597 K）、Ema（6.081 K）和Emap（1.1935%）分别都比BPNN的（Er=18.1325 K、Ema=12.6657 K、Emap= 2.5254%）要小得多。这些结果再次表明，在Al基非晶合金数据集上，PSO-SVR与BPNN相比，具有更高的预测精度以及更强的泛化能力。

表3 两种回归方法预测性能的比较Table 3 Comparison of prediction performance between BPNN and PSO-SVR

在不同Al-TM-RE系中，使用统计学方法很难得到确定的化学混合焓∆Hmix、拓扑不稳定参数λ、电负性差∆x、参数（6x+11y）以及用有效原子半径修正后的拓扑不稳定参数λ′等参数来区分合金的晶化类型。而PSO-SVR方法解决了使用Al基非晶参数不能准确分析其热稳定性的问题。以上结果表明：PSO-SVR能用于预测Al基非晶合金的Tx值，并具有很好的预测精度和泛化能力。

4 结论

1） 将机器学习方法与材料研究相结合，根据 Al基非晶合金的表征参数，采用基于 LOOCV的PSO-SVR预测方法，对不同体系Al基非晶合金的Tx进行建模和预测研究，并将其预测结果与BPNN模型的预测结果进行了比较。其中 PSO-SVR预测结果的Er（7.6597 K）、Ema（6.081 K）和Emap（1.1935%）分别都比BPNN的（Er=18.1325 K、Ema=12.6657 K、Emap= 2.5254%）要小得多。

2） 由于PSO-SVR的预测方法比BPNN方法具有更高的预测精度和更强的泛化能力，而面向Al基非晶合金的数据集的实验结果也同样证明了这个结论。因此，PSO-SVR预测方法对该方向的物理实验具有一定的指导意义和实用价值。

REFERENCES

［1］ GLORIANT T， GREER A L. Al-based nanocrystalline composites by rapid solidification of Al-Ni-Sm［J］. Nanostructured Materials， 1998， 10: 389−396.

［2］ SAHOO K L， SAHU R， GHOSH M， CHATTERJEE S. Studies on crystallization behavior and mechanical properties of Al-Ni-La metallic glasses［J］. Bulletin of Materials Science， 2008，31（3）: 433−439.

［3］ 盈 亮， 戴明华， 胡 平， 闫巧云. 6061-T6铝合金高温本构模型及温成形数值模拟［J］. 中国金属有色学报， 2015， 25（7）: 2815−1821. YING Liang， DAI Ming-hua， HU Ping， YAN Qiao-yun. Thermal constitutive model and numerical simulation of hot forming for 6061-T6 aluminum alloy［J］. The Chinese Journal of Nonferrous Metals， 2015， 25（7）: 2815−1821.

［4］ ZHONG Zhen-chen， JIANG Xiang-yang， GREER A L. Micro structure and hardening of Al-based nanophase composites［J］. Materials Science and Engineering A， 1997， 226: 531−535.

［5］ 李永飞， 王英敏， 耿遥祥， 王传龙， 韩凯明， 羌建兵， 高晓霞，米少波， 王 清， 董 闯， 孙继忠. Ni60Nb40与Ni40Nb60非晶合金的低温晶化行为［J］. 中国金属有色学报， 2014， 24（10）: 2588−2593. LI Yong-fei， WANG Ying-min， GEN Yao-xiang， WANG Chuan-long， HAN Kai-ming， QIANG Jian-bing， GAO Xiao-xia，MI Shao-bo， WANG Qing， DONG Chuang， SUN Ji-zhong. Low-temperature crystallization behavior of Ni60Nb40and Ni40Nb60metallic glasses［J］. The Chinese Journal of Nonferrous Metals， 2014， 24（10）: 2588−2593.

［6］ LISBOA R D S， BOLFARINI C， BOTTA W J F. Topological instability as a criterion for design and selection of aluminumbased glass-former alloys［J］. Applied Physics Letters， 2005，86（21）: 211904.

［7］ EGAMI T， WASEDA Y. Atomic size effect on the formability of metallic glasses［J］. Journal of Non-Crystalline Solids， 1984，64（1/2）: 113−134.

［8］ ZHANG Zhang， ZHOU Wei， XIONG Xian-zhong， KONG Ling-tao， LI Jin-fu. Glass forming ability and primary crystallization behavior of Al-Ni-Ce alloys［J］. Intermetallics，2012， 24: 1−6.

［9］ ZHANG Long， ZHANG Fan， YANG Xi， LONG Guan-kui， WU Ying-peng， ZHANG Peng-fei， LENG Kai， HUANG Yi， MA Yan-feng， YU Ao， CHEN Yong-sheng. Porous 3D graphenebased bulk materials with exceptional high surface area and excellent conductivity for supercapacitors［J］. Scientific Reports，2013， 3: 1408.

［10］ JIA Ran， BIAN Xiu-fang， LUE Xiao-qian， SONG Kai-kai， LI Xue-lian. The relationship between viscosity and glass forming ability of Al-（Ni）-Yb alloy systems［J］. Science China Physics，Mechanics and Astronomy， 2010， 53（3）: 390−393.

［11］ 张 章， 熊贤仲， 乙姣姣， 李金富. Al-Ni-RE 非晶合金的晶化行为和热稳定性［J］. 物理学报， 2013， 62（13）: 136401. ZHANG Zhang， XIONG Xian-zhong， YI Jiao-jiao， LI Jin-fu. Crystallization behavior and thermal stability of Al-Ni-RE metallic glasses［J］. Acta Physica Sinica， 2013， 62（13）: 136401.

［12］ BOER F R， PERRIFOR D G. Cohesion in metals［M］. Netherlands: Elsevier Science Publishers， 1988: 20−35.

［13］ 徐 戎， 李落星， 张立强， 朱必武， 卜晓兵. 金属型铸造界面换热系数峰值预测模型的建立和验证［J］. 中国金属有色学报，2014， 24（4）: 950−957. XU Rong， LI Luo-xing， ZHANG Li-qiang， ZHU Bi-wu， BU Xiao-bing. Development and validation of prediction models of heat transfer coefficient peak value during metal casting process［J］. The Chinese Journal of Nonferrous Metals， 2014，24（4）: 950−957.

［14］ VAPNIK V N. The nature of statistical learning theory［M］. New York: Springer-Verlag， 1995: 53−64.

［15］ CAI Cong-zhong， WANG Wan-lu， SUN Li-zhi， CHEN Yu-zong. Protein function classification via support vector machine approach［J］. Mathematical Biosciences， 2003， 185（2）: 111−122.

［16］ 温玉锋， 蔡从中， 裴军芳， 朱星键， 肖婷婷. R2O-MO-Al2O3-SiO2玻璃配方与热膨系数关系的支持向量回归研究［J］. 功能材料， 2009， 40（1）: 66−70. WEN Yu-feng， CAI Cong-zhong， PEI Jun-fang， ZHU Xing-jian，XIAO Ting-ting. Study on the relationship between thermal expansion coefficient and oxide composition of R2O-MO-Al2O3-SiO2system glass via support vector regression approach［J］. Journal of Functional Materials， 2009， 40（1）:66−70.

［17］ ABUOMAR O， NOURANIAN S， KING R， RICKS T M， LACY T E. Comprehensive mechanical property classification of vapor-grown carbon nanofiber/vinyl ester nanocomposites using support vector machines［J］. Computational Materials Science，2015， 99: 316−325.

［18］ MAJID A， KHAN A， JAVED G， MIRZA A M. Lattice constant prediction of cubic and monoclinic perovskites using neural networks and support vector regression［J］. Computational Materials Science， 2010， 50（2）: 363−372.

［19］ OWOLABI T O， AKANDE K O， OLATUNJI S O. Development and validation of surface energies estimator （SEE）using computational intelligence technique［J］. Computational Materials Science， 2015， 101: 143−151.

［20］ CORTES C， VAPNIK V. Support-vector networks［J］. Machine Learning， 1995， 20（3）: 273−297.

［21］ PENG Si-hua， XU Qiang-hua， LING Xuefeng-bruce， PENG Xiao-ning， DU Wei， CHEN Liang-biao. Molecular classification of cancer types from microarray data using the combination of genetic algorithms and support vector machines［J］. FEBS Letters，2003， 555（2）: 358−362.

（编辑 龙怀中）

Parameters analysis of Al-based amorphous alloys using support vector regression

XU Yan1， ZHANG Yu-feng1， GAO Tian1， ZHANG Yan2， ZHANG Hui-ran2， LIU Yong-sheng1
（1. School of Mathematics and Physics， Shanghai University of Electric Power， Shanghai 201399， China；2. School of Computer Engineering and Science， Shanghai University， Shanghai 200444， China）

According to the experimental data of Al-based amorphous alloys， a model to predict the crystallization temperature Txof Al-based amorphous alloys by using particle swarm optimization combined with support vector regression （PSO-SVR） was established. Based on this model， crystallization temperature Txcan be predicted， and then compared with the method of back-propagation neural network （BPNN）. The results show that the prediction error is smaller by using PSO-SVR. This means that the crystallization behavior and thermal stability of Al-based amorphous alloys can be well described by the parameters used in PSO-SVR model. Moreover， the PSO-SVR model could provide an important theoretical and practical guidance to the research on Al-based amorphous alloys.

Al-based amorphous alloy； crystallization temperature； support vector regression； particle swarm optimization

Project（12ZZ174） supported by Innovation Program of Shanghai Municipal Education Commission，China； Project（12CG63） supported by Shanghai Educational Development Foundation of Chenguang Program， China

date： 2015-08-11； Accepted date： 2015-11-28

XU Yan； Tel: +86-18918778925； E-mail: xuyan@shiep.edu.cn

TB34

A

1004-0609（2016）-04-0836-08

上海市教委科研创新资助项目（12ZZ174）；上海市教育发展基金会晨光计划资助项目（12CG63）

2015-08-11；

2015-11-28

徐 燕，讲师，博士；电话：18918778925；E-mail: xuyan@shiep.edu.cn