单漏斗放矿柔性隔离层界面形态演化规律

陈庆发，陈青林，仲建宇，陈大鹏，李诗华，牛文静

（广西大学 资源与冶金学院，南宁 530004）

单漏斗放矿柔性隔离层界面形态演化规律

陈庆发，陈青林，仲建宇，陈大鹏，李诗华，牛文静

（广西大学 资源与冶金学院，南宁 530004）

采用Origin软件对隔离层界面形态演化观测数据进行拟合，并对高斯模型参数进行理论分析和统计分析，构建隔离层界面剖面整体动态函数表达式；将实测隔离层界面形态曲线与动态函数式进行比较，在力学分析基础上，推导底部类似抛物线形状的函数表达式，解出函数分界点坐标。两项函数式共同构成完整的隔离层界面形态数学模型。研究成果为柔性隔离层作用下散体介质流理论体系的系统构建打下坚实基础。

放矿；单漏斗；柔性隔离层；界面形态；演化规律；高斯模型

在绿色开采、无废开采、协同开采等理念［1-4］指导下，本文作者 2010年提出了“同步充填”采矿技术理念，并发明了一种大量放矿同步充填无顶柱留矿采矿方法［5］。新采矿方法中散体介质因柔性隔离层的存在，其流动规律突破了现有放矿理论描述范围，因此，开展柔性隔离层作用下散体介质流理论研究具有重要意义。其中，柔性隔离层界面形态演化规律是该理论研究的重要内容之一。

有关隔离层及相关放矿规律研究，在20世纪50年代，就有人提出矿石隔离层下放矿的设想［6］；20世纪70年代，研究人员进行了“细碎矿石隔离层”降低贫化的新工艺试验［7］；董鑫等［8］分析了无底柱分段崩落法矿石隔离层下放矿理论的可行性，文义明［9］采用“造团”技术形成隔离层有效控制上部细小废石颗粒穿流。但这些隔离层仍然指的是矿岩介质，与本申请项目之柔性隔离层具有较大差异。侯建华等［10］在干式充填采矿法应用时曾提出将麻布袋、废旧运输胶带、草廉等柔性材料作为隔离层，但该采矿工艺中仅将隔离层作为垫层作用，隔断底部废石，不存在隔离层下沉规律研究。

仿照经典放矿学理论，本文作者在单漏斗放矿试验条件下，对柔性隔离层界面形态演化规律进行分析与研究，以期构建柔性隔离层作用下散体介质流理论体系。

1 试验记录及演化规律基本描述

在实施大量放矿同步充填工艺室内相似试验过程中，每放出一定量的矿石后，记录隔离层界面下降深度h，并用高速相机拍摄记录隔离层界面的形态位置，记录情况如图1所示（因图片较多，只列举4张代表性的）。并将图1曲线绘制在一张图上，可以很明显看出隔离层界面动态演化过程，如图2所示。

由图2可知，未放矿时隔离层呈直线水平状态，当打开放矿漏斗口后，随着模型中矿石的不断放出，隔离层在回填废石载荷力与矿石散体流动场共同作用下，逐渐弯曲变形且随矿石流动一起下降；放出一定量后，在隔离层下部出现了明显的空腔，且空腔体积不断扩大。在模型剖面上，隔离层界面整体上呈现出高斯曲线形态；但放矿过程中的空腔使底部隔离层与矿石分离，底部隔离层在上覆载荷与两侧隔离层拉力的作用下呈现出类似抛物线形状。尤其在放矿后期，底部隔离层类似抛物线形状愈加显著。

2 隔离层界面形态初始动态模型

根据物理模型设计特点（坐标原点设置在物理模型下边缘的中点），每隔一定柔性隔离层下降深度h，描绘出此深度下柔性隔离层的（x，y）坐标。将各组（x，y）值依次输入到Origin数据处理软件中，对各组数据分别用Gauss拟合，各组回归相关系数都在0.9以上，故高斯模型可以很好地吻合各条曲线，相关参数汇列于表1。

图1 隔离层界面形态实验图Fig. 1 Experiment graphs of ore-drawing morphologies of isolation layer: （a） Third time ore-drawing isolation layer； （b） Seventh time ore-drawing isolation layer； （c） Tenth time ore-drawing isolation layer； （d） Ore-drawing end curve of isolation layer

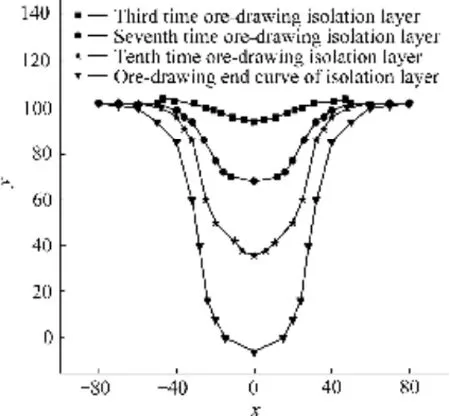
图2 隔离层界面形态动态演化图Fig. 2 Dynamic evolutions of ore-drawing morphologies of isolation layer

表1 隔离层拟合参数Table 1 Fitting parameters of isolation layer

高斯模型基本式为

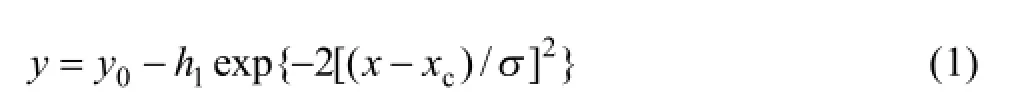
基于高斯基本式可构建出剖面上整体呈现出高斯曲线形态的隔离层形态初始模型。式（1）中y0、h1、xc、σ参数不具备任何物理意义，需在理论上建立各参数与隔离层形态初始模型参数之间的物理与数值关系。

基于高斯分布公式具有的集中性、对称性、标准差 σ决定了分布的幅度、3σ法则等特征［11-12］和本次试验自身特点，对参数进行理论分析及修正。

1） y0参数

当x趋于无穷大时。由高斯分布3σ法则特征可知：

结合试验特点明显可知，y0等于隔离层初始位置在网格的纵坐标值H，即y0=H。

2） xc参数

结合高斯分布集中性与对称性和试验隔离层最低点位于X=0，即xc=0。

3） h1参数

通过对y0、xc分析，可将式（1）作如下改写：

先对特殊点x=0进行分析，得出h1=h。然后结合特殊点x=0的结论对曲线的一般性进行分析，利用反证法论证思维并结合高斯分布特点，易得出h1=h为通解。

4） σ参数

σ参数是刻画隔离层在散体载荷作用下其形态分散程度的一个量，因此，影响σ参数大小的因素主要是散体与隔离层自身物理力学性质和隔离层下降深度h，其关系可用σ=f（α，β，h）表示。

据表1，对σ与h关系进行线性拟合，得

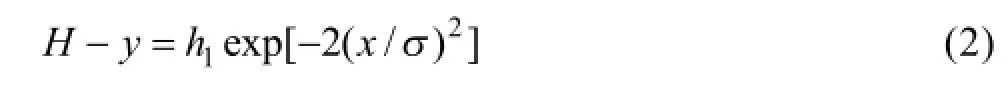
综上可得隔离层形态初始动态模型：

3 界面形态剖面整体动态函数式

y0、xc、h1参数均在理论上建立了与初始动态模型参数在数值上的相等关系，还需要利用统计学原理对数据做有效的检验。

现对各参数等式做变换如下：

X1、X2、X33个母体均符合正态分布其中2σ未知。在各母体上作假设H1：假设 H2： 0==02μμ；假设H3： 0==03μμ。

表2 各母体统计量计算量表Table 2 Statistics and computational complexity of each parent

由表 2可知，假设 X1、X2均无显著差异，只有X3存在显著差异，则h1与h不存在数值上的相等关系，故须应对h1=h作进一步的修正处理。通过回归h1与h的数据（见图3），可知h1与h存在线性关系，即对h1与h做如下修正处理。

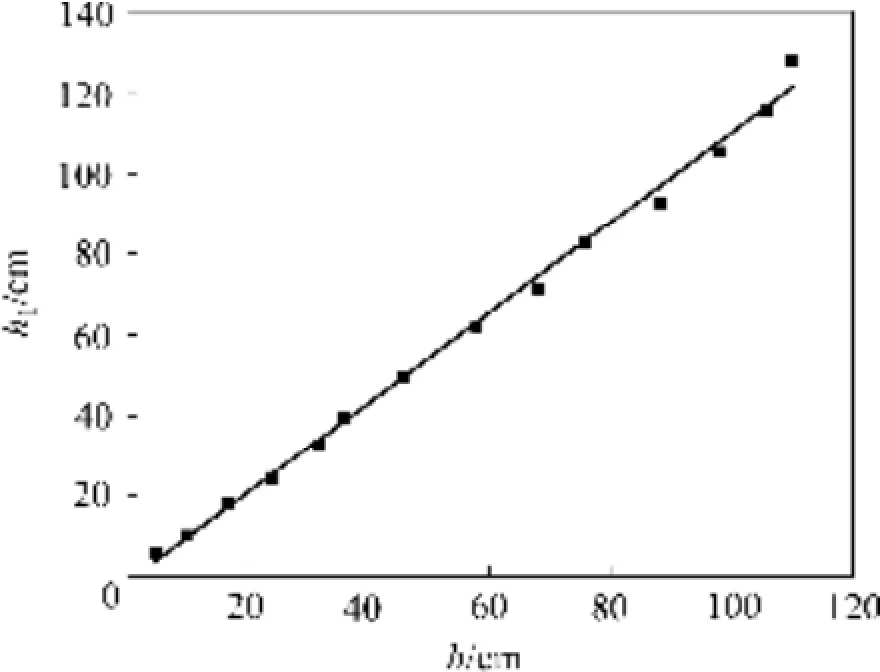
图3 h1与h关系趋势图Fig. 3 Tendency between h1and h

计算可得1204.1=λ，即得出隔离层界面形态的动态函数式为

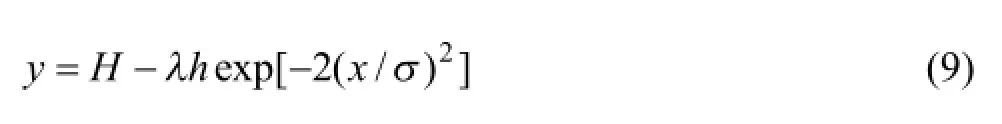
式中：H为隔离层初始纵坐标；h为隔离层下降深度；σ为隔离层曲线标准差；1204.1=λ。

4 实测界面曲线与动态函数式比较

图4和5所示分别为第5次与放矿终了隔离层曲线与拟合曲线对比图。从图4和5可看出，式（9）拟合曲线与隔离层曲线在底部偏差较大，尤其是随着隔离层下降深度的增加，差异性更加明显，在放矿终了时最低点误差［13］到达

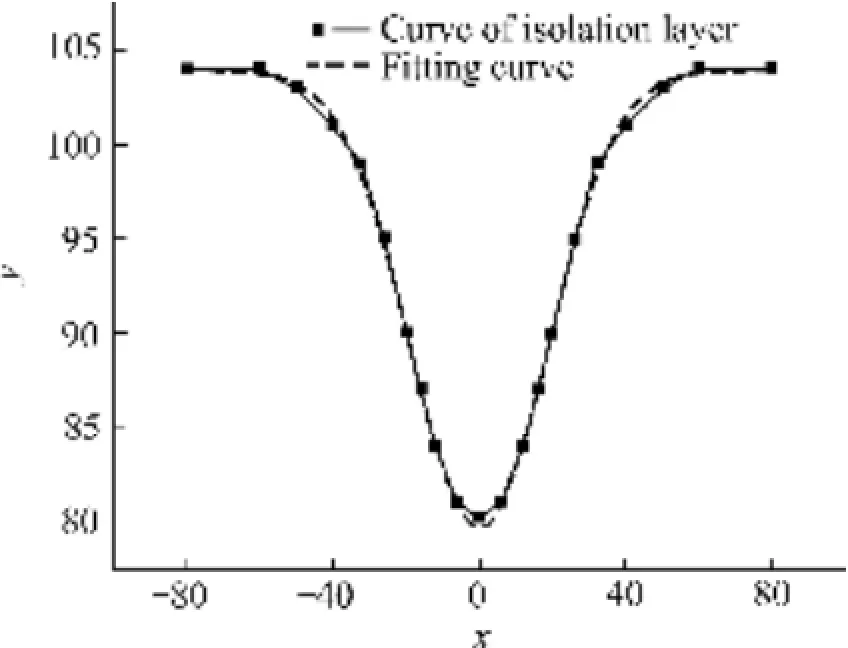
图4 第5次隔离层曲线与拟合曲线对比图Fig. 4 Comparison of 5th times curves of isolation layer with fitting curve

图5 放矿终了隔离层曲线与拟合曲线对比图Fig. 5 Compare ore-drawing end curve of isolation layer with fitting curve

虽然式（9）拟合曲线精度较高，但因放矿中空腔的存在，隔离层在横向荷载作用下，底部隔离层下沉受到限制。大量放矿后期，隔离层底部空腔不断扩大，隔离层曲线与拟合曲线在底部偏差逐渐增大。且由h1与h之间的数值关系可推知隔离层曲线与拟合曲线在底部偏差逐渐增大。因此，隔离层动态函数式在底部不具有较强适用性，需另寻一种函数来描述此部分隔离层界面形态。

5 底部隔离层界面形态函数式确定

底部隔离层的弯曲变形受上覆散体载荷影响，呈现为类似抛物线形。由于隔离层的重量对隔离层变形影响比上覆散体载荷对隔离层变形影响很小，故忽略不计。散体和隔离层整体受力状态见图6。

图6段散体和隔离层整体受力分析图Fig. 6 Force analysis of loose medium in segment and whole isolation layer

设隔离层最低点为A，取y轴通过点A铅直向上，并取x轴水平向右，且取垂直纸面宽度为一个单位长度，设隔离层曲线方程为y=y（x），现考察点A到另一点M（x，y）间的一段，段散体两侧侧压力分别为p1、p2，其所受重力为G，密度为ρ，高度为h。因隔离层为柔性材料，所以在点A处张力沿水平的切线方向，其大小为N，在点M处的张力沿该点的切线方向，设其倾角为θ，其大小为T。

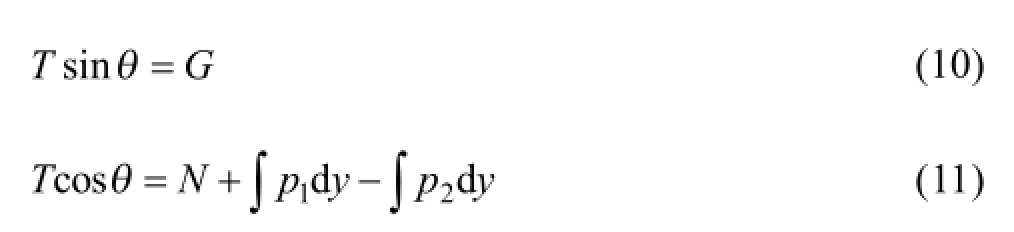
将式（10）除于式（11）得

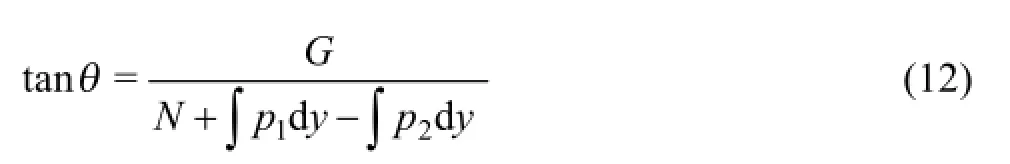
散体侧压力［17］表示式：

式中：kc为侧压力系数；ρ为散体密度；g为重力加速度；h′为深度。

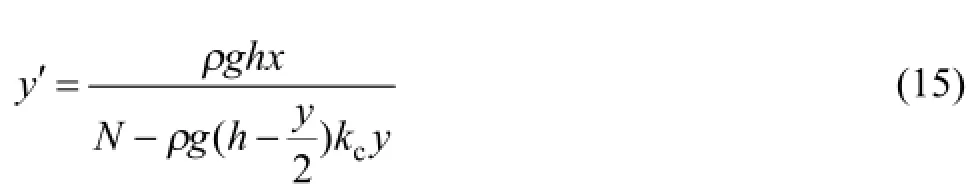
分析中的坐标原点取在隔离层最低位置，即可得初始条件为

利用式（16）初始条件对式（15）一阶微分方程求解，即可得出底部隔离层界面的函数表达式：

6 隔离层界面完整函数式综合确定

式（9）坐标原点是试验模型的原点，而式（17）的坐标原点是隔离层的最低点坐标，为使两方程在坐标原点上达到一致性，对式（17）做X=0、Y=y+H-h坐标变换得

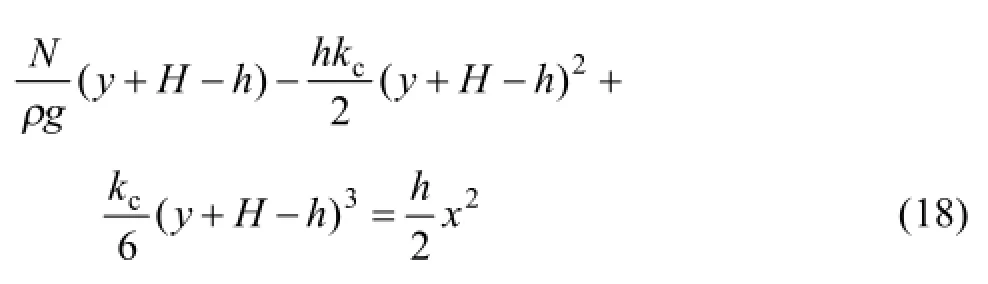
式（18） 分析基础是只有上覆载荷，故不适用于空腔边界以外的隔离层形态曲线。式（9）在空腔边界的误差值如表3所列。由表3可知，式（9）表达的曲线在空腔处误差值较小，可把空腔边界作为式（9）和（18）隔离层界面形态表达函数的分界点。

表3 空腔边界处误差值表Table 3 Error values of boundary on cavity

空腔边界的倾角是随着隔离层的逐渐下沉增大到散体自然安息角wφ 后不变，将式（15）和（17）联立求解可得边界点方程：

式中：φ为空腔边界倾角；其他符号意义同前。

由式（19）可解空腔边界倾角为φ时边界纵坐标唯一实根y1，并可由y1反代入式（15）或（17）可解边界横坐标正根x1。即可得完整隔离层形态的数学模型：

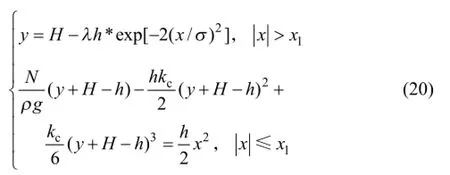
式中：H为隔离层初始纵坐标；h为隔离层下降深度；σ为标准差；1204.1=λ；N为隔离层最低点张力；ρ为散体密度；ck为侧压力系数。

7 结论

1） 利用Origin拟合回归各组柔性隔离层的坐标，在比较相关系数的基础上，引入高斯模型作为剖面上整体隔离层形态数学模型基本式。

2） 建立了基本式中各参数与对应隔离层形态初始动态模型参数之间的物理意义，利用统计学原理对各参数进行检验。在试验数据的基础上得出了剖面上整体的隔离层界面形态的动态函数式。

3） 通过实测隔离层曲线与动态函数式分析比较，在力学分析的基础上推导了底部隔离层界面形态的函数式。

4） 结合底部函数式适用情况，分析了适用性分界点，得出完整隔离层界面形态的数学模型。

REFERENCES

［1]钱鸣高. 绿色开采的概念与技术体系［J］. 煤炭科技， 2003，24（4）: 1-3. QIAN Ming-gao. Technological system and green mining concept［J］. Coal Science and Technology Magazine， 2003， 24（4）: 1-3.

［2]BRUE F， JEFFREY S， LINDA G， FERN Z. Balancing environmental and industry sustainability: A case study of the US gold mining industry［J］. Journal of Environmental Management， 2009， 90（12）: 3690-3699.

［3]陈庆发， 周科平， 古德生. 协同开采与采空区协同利用［J］. 中国矿业， 2011， 20（12）: 77-80， 102. CHEN Qing-fa， ZHOU Ke-ping， GU De-sheng. Synergetic mining and cavity synergetic utilization［J］. China Mining Magazine， 2011， 20（12）: 77-80， 102.

［4]陈庆发， 苏家红. 协同开采及其技术体系［J］. 中南大学学报（自然科学版）， 2013， 44（2）: 732-737. CHEN Qing-fa， SU Jia-hong. Synergetic mining and its technology system［J］. Journal of Central South University （Science and Technology）， 2013， 44（2）: 732-737.

［5]陈庆发， 吴仲雄. 大量放矿同步充填无顶柱留矿采矿方法:中国， 201010181971.2［P］. 2010-10-20. CHEN Qing-fa， WU Zhong-xiong. A large number of ore drawing synchronous filling no-top-pillar shrinkage stoping method: CN， 201010181971.2［P］. 2010-10-20.

［6]MALAKHOV Γ M. 崩落矿块的放矿［M］. 北京: 冶金工业出版社， 1958: 14-15. MALAKHOV Γ M. Drawing of caving ore block［M］. Beijing: Metallurgical Industry Press， 1958: 14-15.

［7]刘国栋. 崩落采矿法采用细碎矿石隔离层降低贫损的研讨［J］.湖南冶金， 1997， 25（3）: 30-33. LIU Guo-dong. Study and discussion on decreasing ore dilution and loss of the caving method by using fine ore barrier［J］. Hunan Metallurgy， 1997， 25（3）: 30-33.

［8]董鑫， 柳小波. 基于 SLS系统的崩落法矿石隔离层下放矿研究［J］. 金属矿山， 2009（6）: 27-28. DONG Xin， LIU Xiao-bo. Study of the ore-drawing under ore isolating layer in caving based on SLS system［J］. Metal Mine，2009（6）: 27-28.

［9]文义明. 小粒径废石覆盖层下放矿贫化控制方法研究［D］. 昆明: 昆明理工大学， 2012: 43-46. WEN Yi-ming. The study of drawing dilution controlling method under the overburden of small grain waste［D］. Kunming: Kunming University of Science and Technology， 2012: 43-46.

［10］ 侯建华， 梁凯河. 干式充填采矿法采场铺垫材料的选择［J］.黄金， 2009， 30（7）: 33-37. HOU Jian-hua， LIANG Kai-he. Choice of stope matting material for dry type back-filling mining method［J］. Gold， 2009， 30（7）: 33-37.

［11］ GATTI P L. Probability theory and mathematical statistics for engineer［M］. Florida: CRC Press， 2004: 41-50.

［12］ 刘沐宇， 徐长佑. 基于证据理论的岩体力学参数信度估计方法［J］. 中国有色金属学报， 2000， 10（4）: 609-612. LIU Mu-yu， XU Chang-you. Belief estimation of rock mass mechanical parameters based on evidence theory［J］. The Chinese Journal of Nonferrous Metals， 2000， 10（4）: 609-612.

［13］ 殷作如， 邹友峰， 邓智毅， 张瑞玺. 开滦矿区岩层与地表移动规律及参数［M］. 北京: 科学出版社， 2008: 122-123. YIN Zuo-ru， ZOU You-feng， DENG Zhi-yi， ZHANG Rui-xi. Rock stratum and ground movement laws and parameters in Kailuan mining area［M］. Beijing: Science Press， 2008: 122-123.

［14］ 黄 炎. 绳索的大变形问题［J］. 力学与实践， 1999， 21（2）: 49-51. HUANG Yan. The large deformation of rope［J］. Mechanics in Engineering， 1999， 21（2）: 49-51.

［15］ ZHOU Wei， TIAN Hong-qi. A novel finite element model for single-layered wire strand［J］. Journal of Central South University， 2013（6）: 1767-1771.

［16］ CHO T， SONG M K. Structural reliability of a suspension bridge affected by environmentally assisted cracking［J］. KSCE Journal of Civil Engineering， 2006， 10（1）: 21-31.

［17］ 顾慰慈. 挡土墙土压力计算手册［M］. 北京: 中国建筑工业出版社， 2005: 20-21. GU Wei-ci. Handbook of retaining wall earth pressure calculation［M］. Beijing: China Architecture and Building Press，2005: 20-21.

（编辑 王 超）

Evolution law of interface morphology of flexible isolation layer under ore drawing from single funnel

CHEN Qing-fa， CHEN Qing-lin， ZHONG Jian-yu， CHEN Da-peng， LI Shi-hua， NIU Wen-jing
（College of Resources and Metallurgy， Guangxi University， Nanning 530004， China）

The observation data of interfacial morphological evolution of the isolation layer were fitted by Origin software， and the parameters of Gauss model were analyzed theoretically and statistically， and the dynamic function expression of the whole interfacial profile of isolation layer was established. Then， actual measured curves of isolation layer and dynamic function expression were compared， and the function expression of bottom shape which is similarly a parabola was derived， and the function boundary point coordinates were solved on the basis of mechanical analysis. The mathematical model of interfacial morphology of whole isolation layer was constituted by these two function expressions. Research results could be regarded as a solid foundation for the construction of the loose medium flow field theoretical system with flexible isolation layer.

ore drawing； single funnel； flexible isolation layer； interface morphology； evolution law； Gauss model

Project（51464005） supported by the National Natural Science Foundation of China

date： 2015-09-08； Accepted date： 2016-01-20

CHEN Qing-fa； Tel: +86-771-3232274； E-mail: chqf98121@163.com

TD801

A

1004-0609（2016）-06-1332-07

国家自然科学基金资助项目（51464005）

2015-09-08；

2016-01-20

陈庆发，教授，博士；电话；0771-3232274；E-mail: chqf98121@163.com