结构性软黏土一维压缩变形特性的数学描述

柯文汇，陈　健，盛　谦，房　强，卞晓曼，赵　青



结构性软黏土一维压缩变形特性的数学描述

柯文汇1，2，陈健1，盛谦1，房强1，卞晓曼1，赵青1

（1．中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，武汉430071；2．武汉市市政建设集团有限公司，武汉430023）

为了研究结构性软黏土一维压缩变形特性的影响，在软黏土一维压缩结构破坏特征的基础上，揭示了压缩指数随孔隙比的变化规律，提出了土体结构渐进破坏的数学描述模式；基于上述描述模式，首先推导了一维压缩曲线的数学表达式，分析了结构效应参数对压缩曲线性状的影响规律；然后利用10种典型结构性软黏土的一维压缩试验结果对数学描述模式进行了验证，并以Mexico City clay为例，将描述模式和其他6种常用描述模式的模拟效果进了对比分析；最后分析了软黏土结构效应参数随（w-wP）的变化规律，通过线性回归得出了结构效应参数的经验关系式。研究结果表明提出的描述模式能较准确地描述一维条件下结构性软黏土的压缩变形的结构破坏特征。成果为建立结构性软黏土的本构模型提供了一定的理论基础，也为进一步研究结构性软黏土的变形特性提出了新的思路。

软黏土；土体结构性；结构破坏；压缩特性；数学描述；原始压缩曲线；结构效应参数

doi：10．11988/ckyyb．20150322

1　研究背景

天然软黏土在长期的自然沉积过程中，发生蠕变、触变、黏结、岩化等作用，表现出明显的结构性［1］。Leroueil等［2］、罗爱忠等［3］指出，土体结构（土中颗粒、孔隙的性状、排列形式以及颗粒之间的胶结）是决定土力学特性的一个重要的内在因素。结构性的存在会一定程度增大天然软黏土的强度，当应力超过初始屈服应力后，土体结构开始逐渐破坏，变形刚度亦随之逐渐变化。因此在软黏土的本构模拟过程中充分考虑土体结构性和结构破坏效应是非常重要的。沈珠江［4］曾指出建立土体结构性数学描述模型是21世纪土力学的核心问题。近年来，国内外学者通过引入损伤函数［5］、岩土破损力学理论［6］、扰动状态函数［7］、结构性参数［1，8-9］建立了大量描述结构性软黏土的一维变形特性和结构破坏特征的数学模型。但以上模型均是采用间接方法来描述一维变形的原始压缩曲线，Butterfield［10］提出了“土的自然压缩定律”，即用ln（e+1）-lnp'双对数线性关系式直接描述结构性软黏土的原始压缩曲线（e为孔隙比，p＇为有效固结应力），而Chai等［11］认为ln（e+ec）和lnp'的关系接近于线性（ec为参数）。但是以上直接描述方法不能准确描述结构性较强的软黏土的一维压缩特性。为此，本文基于压缩指数随孔隙比的变化规律，提出了结构性软黏土一维压缩曲线的更为直接的数学描述，并利用典型结构性软黏土的试验结果验证了本文描述模式的有效性，最后探讨了结构效应参数的经验关系式。

2　描述模式的提出

2．1一维压缩的结构破坏效应特征

结构性软黏土的一维压缩试验［1-4］表明，加载过程中土体结构的逐渐破坏使压缩曲线在e-lnp'坐标中呈现明显的非线性，如图1所示。结构性软黏土一维压缩的结构破坏效应特征主要表现为以下3个方面。

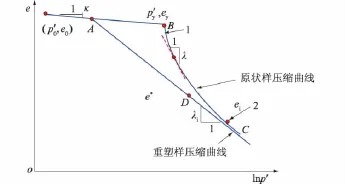
图1　结构性土和重塑土的一维压缩曲线示意图Fig．1　One-dimensional compression curves forstructured clays and reconstituted clays

（1）荷载增大到初始结构屈服应力，软黏土开始出现结构屈服和破坏，土体的微观结构大面积坍塌，颗粒大规模破碎，孔隙比急剧减小，变形急剧增大，此时结构性软黏土表现为很高的压缩性，e-lnp'曲线较陡，压缩指数λ（即e-lnp'曲线的切线斜率）较大。

（2）当荷载进一步增加时，土体结构进一步破坏，破碎的颗粒、滑移的粒团和坍塌的“结构废墟”会逐渐滑入并充实土体孔隙，使孔隙比逐渐减小，土体逐渐密实。土体越密实，土中的颗粒间越不容易发生滑移、滚动等排列重组，表现为土体的压缩性逐渐变小。在e-lnp'曲线中相应点逐渐变缓，λ逐渐变小。

（3）当荷载增大到一定程度时，土体结构破坏殆尽，原状样的压缩性接近重塑样的压缩性，结构性软黏土e-lnp'曲线的后半段将逐渐趋近重塑样的elnp'曲线，λ逐渐趋于重塑样的固有压缩指数λ1。

2．2描述模式的提出

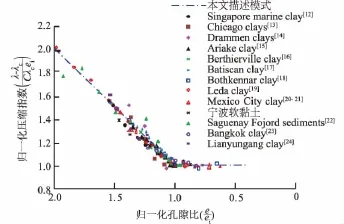
图2　结构性软黏土压缩指数与孔隙比的关系Fig．2　Relationship between compression index andvoid ratio for structured soft clays

图2是几种典型结构性软黏土一维压缩试验的压缩指数随着孔隙比的变化规律。由图2知，结构破坏初期压缩指数λ随着孔隙比e近似线性减小，当e减小到一定程度时，压缩指数λ将趋于固有压缩指数λi值，在此基础上，本文提出了一个基于孔隙比的软黏土一维压缩结构破坏效应的新型描述模式，即

式中：ey为初始结构屈服点（图1中B点）对应孔隙比；ei为结构性软黏土λ衰减为λi时的孔隙比，如图1中C点所示；D代表λ随孔隙比的衰减速率。

i是用来描述土体结构破坏的参数。

3　一维压缩曲线的数学表述

3．1结构屈服段数学表达式

由压缩指数λ的定义可以将式（2）写成

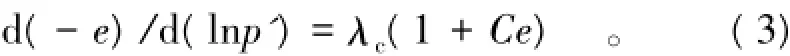
对式（3）变换形式并积分得

式中：py＇为结构屈服应力；ey为初始屈服孔隙比。

当C→0时，式（4）能退化为重塑样的e-lnp'线性关系；当C=1时，式（4）退化为Den Haan［25］提出的“土的自然压缩定律”。］，式（4）可写

3．2卸载-再加载段数学表达式

根据经典土力学，结构性软黏土的卸载-再加载曲线（图1中AB段）的数学表达式为

大量的试验结果表明，回弹指数κ只有压缩指数λ的1/5～1/10，卸载-再加载段的变形很小，式（6）两边同乘以常数C/（1+Cey），根据无穷小的概念，式（6）可近似写成

式中κc=κ/（1+Cey）。结合εn的定义，由式（7）可进一步改写为nn

式（8）与式（5）有相同的形式，共同描述了结构性软黏土的一维压缩曲线，且与经典土力学重塑样一维压缩线的ε-lnp'表达式形式相同。成

4　结构效应参数对压缩曲线的影响

4．1ei值对压缩曲线的影响

给定一组参数，分别计算不同的ei值对应的压缩曲线，如图3所示。

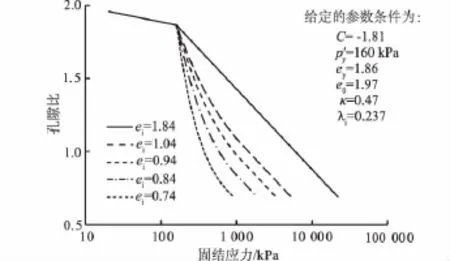
图3　ei对原始压缩曲线的影响Fig．3　Influence of eion virgin compression curves

由图3知，随着ei的增大，结构性软土原始压缩曲线均表现出斜率（坡度）由陡变缓，最后逐渐趋于稳定值的共同特征。原始压缩曲线（结构屈服段）起始段的斜率随着ei的减小而不断增大，斜率趋于稳定（土体结构完全破坏）之前需要的变形也随着ei的减小而不断增大。特别地，当ei=1．84且接近ey时，即不考虑结构性的影响时，原始压缩曲线近似于重塑样的正常固结线。随着ei值的减小，原始压缩曲线的结构破坏效应也越来越明显。

4．2C值对压缩曲线的影响

C值对原始压缩曲线的影响如图4所示。从图可以看出，随着C的绝对值的不断增大，原始压缩曲线从左右两边不断向极限压缩曲线（当C=±999 9时的原始压缩曲线）靠拢：当C=0．000 1时（近似为0），应力-应变关系没有表现出结构破坏效应，原始压缩曲线近似于重塑样的正常固结压缩线。随着C （C＞0）值增大，压缩曲线的结构破坏效应越明显。当C＜0时，也有相同的规律，随着C值的增大，压缩指数随孔隙比的减小速率加快，结构破坏的速率会提高。而且，C＜0时原始压缩曲线的结构破坏特征要比当C＞0时显著，一般的结构性软黏土C为负值。

图4　C对原始压缩曲线的影响Fig．4　Influence of C on virgin compression curves

5　一维压缩曲线模拟效果的试验验证

5．1参数确定

描述土体结构破坏的参数包括C和ei。如图1所示，ei可以根据原始压缩曲线形状在高应力阶段近似获取，即当压缩指数接近衰减为固有压缩指数λi时的孔隙比。在结构性软黏土的原始压缩曲线上靠近初始结构屈服点处取一点1，相应的孔隙比和压缩指数分别为ei和λi。由式（2）得到

5．2模拟效果的试验验证

将不同软黏土的结构效应参数和部分基本物理性质汇总于表1中。图5是10种典型的结构性软黏土一维压缩的模拟曲线和试验曲线的对比图。

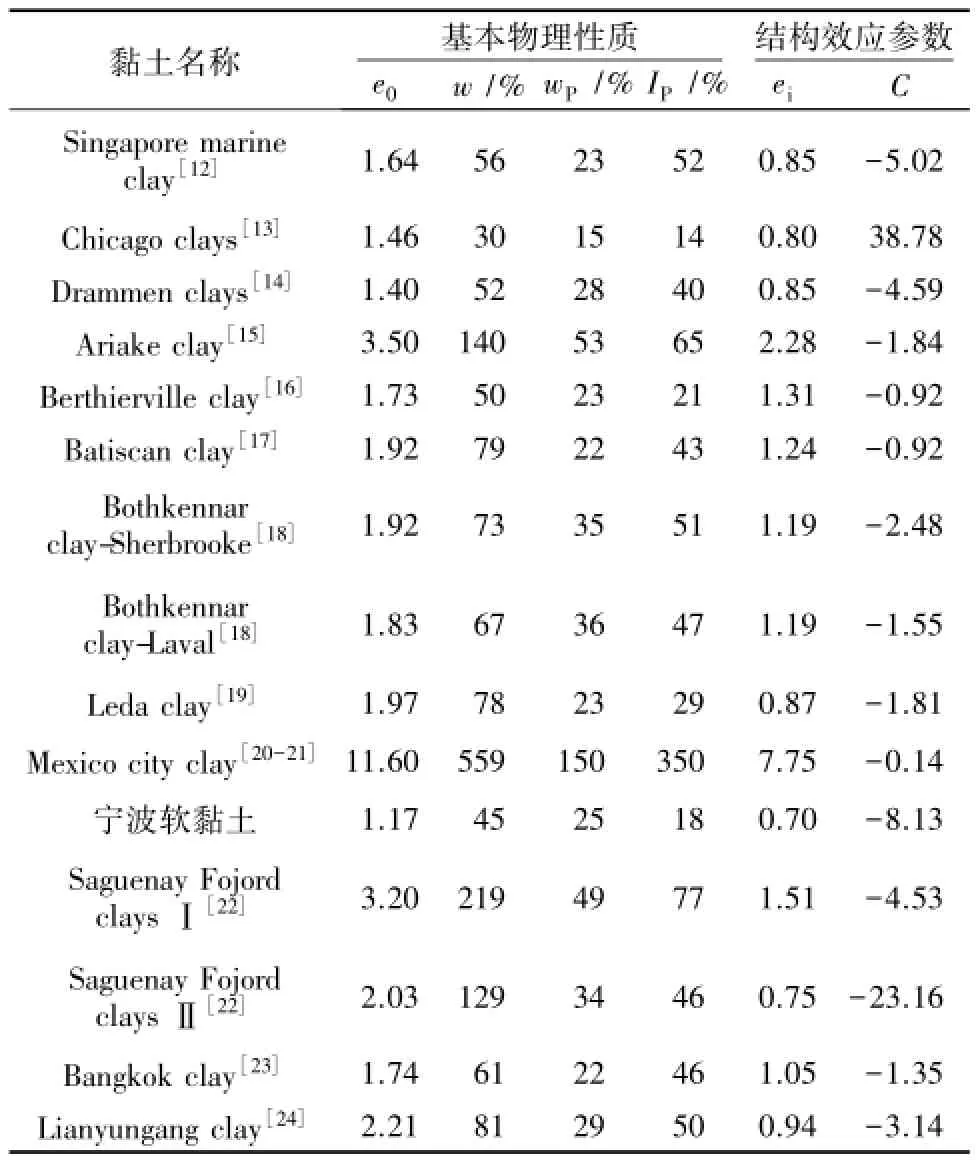
表1　典型黏土结构效应参数和基本物理性质Table 1　Structural effect indexes and physical characteristics of typical clays

由图5可以看出，结构性软黏土压缩曲线在elgp＇坐标中的形状近似于倒“S”形，呈现明显的非线性。计算曲线和试验曲线吻合程度相当高，回归系数R2≥0．98，表明本文模式能准确地反映软黏土一维压缩的结构破坏特征，能有效地描述结构性软黏土的一维压缩变形特性。

图5　典型结构性软土一维压缩的模拟曲线和试验曲线对比Fig．5　Comparisons between simulated and tested curves of 1-D compression for representative structured soft clays

5．3模拟效果的对比分析

以Mexico city clay［20］的一维压缩试验为例，将表2中几种常用的结构性土的压缩特性数学描述与本文描述的模拟效果进行了对比分析，如图6所示。Mexico city clay的基本物理性质见表1。

由图6知，对于结构性较强的Mexico city clay，除了Butterfield模式［10］和 Chai等模式［11］之外，其他模式均能在一定程度上准确地刻画原始压缩曲线的形状。其中，Liu等模式［8］、Yin等模式［9］及Baudet等模式［1］在结构破坏初期能很好地模拟原始压缩曲线，而结构破坏殆尽时会高估土体的变形；Haan模式［25］由于多一个参数而能从整体上较准确地模拟原始压缩曲线；相对于其他模式，本文模式能较准确地描述结构性软黏土的非线性应力-应变关系。

表2　几种常用的结构性软黏土压缩特性描述模式Table 2　Common descriptive modes of compression behaviour of structural soft clays

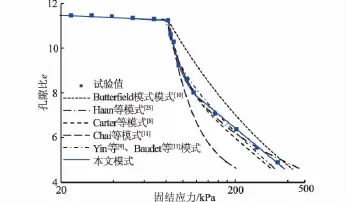
图6　不同描述模式的模拟结果的对比Fig．6　Comparison of simulated results of various descriptive modes on virgin compression curves

6　结构效应参数的经验关系式

由表1可知，对于大多数结构性软黏土，ei约为初始孔隙比e0的40%～70%，而C值大致分布在（-0．1，-5）之间。Chai等［11］经过试验研究发现，当结构性软土由天然含水量w被压缩至塑限含水量wP时，土体结构大部分已破坏，对压缩特性的影响可以忽略。因此，可以用天然含水率和塑限含水率之间的差值（w-wP）来近似度量一维压缩过程中结构效应完全消失之前的体积变化量，而这一体积变化量又可以通过土体结构完全破坏时孔隙比的变化（e0-ei）反映，所以（w-wP）和（e0-ei）必然存在某种相关关系。现将表1中几种典型结构性软土的e0-ei和w-wP的关系统计于图7中。

由图7可知，对于不同的结构性软黏土，e0-ei随着w-wP的增大而近似线性增大，经过线性回归得到结构性软黏土ei的经验公式，即

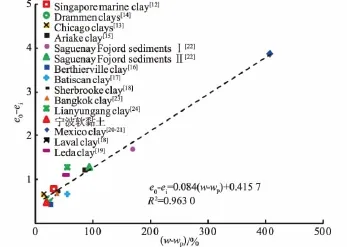
图7　典型结构性土的e0-ei与w-wP的关系Fig．7　Relationship between e0-eiand w-wPfor typical structured clays

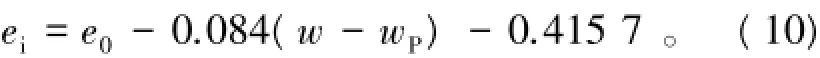
另外，由式（9）可知结构效应参数C与ei并非相互独立，通过式（10）确定ei之后，可结合原始压缩曲线由式（9）近似估计C值。需要强调的是，由于缺乏大量试验资料及试验结果的变异性，本文得出的结构效应参数与物性参数的经验关系式仅是一种向导性的有意义的探索，可以为结构效应参数ei和C的确定提供一定的参考。

7结论

（1）推导了结构性软黏土一维压缩曲线的数学表达式，与重塑样一维压缩线表达式形式相同，可以为非结构性软黏土的本构模型拓展至结构性软黏土提供了一个新的思路。

（2）ei值、C值明显地影响着结构性软土的一维压缩曲线的形状；ei值越小，C值越大，压缩曲线结构破坏效应越明显。

（3）对比了典型结构性软黏土一维压缩的模拟曲线和试验曲线，表明本文模式能准确地反映软黏土一维压缩的结构破坏特征，有效地描述不同结构性软黏土的非线性应力-应变关系。

（4）分析了土体结构完全破坏时孔隙比的变化（e0-ei）随天然含水量和塑限的差值（w-wP）的变化规律，通过线性回归得出了结构效应参数ei的经验公式，并给出了结构效应参数C的经验估计方法，在缺乏相关数据的情况下为结构效应参数ei和C的确定提供一定的参考。

［1］BAUDET B，STALLEBRASS S．A Constitutive Model for Structured Clays［J］．Géotechnique，2004，54（4）：269-278．

［2］LEROUEIL S，VAUGHAN P R．The General and Congruent Effects of Structure in Natural Soils and Weak Rocks［J］．Geotechnique，1990，40（3）：467-488．

［3］罗爱忠，邵生俊，陈昌禄，等．基于综合结构势的结构性黄土双硬化参数模型［J］．长江科学院院报，2013，30（9）：59-63．

［4］沈珠江．土体结构性的数学模型——21世纪土力学的核心问题［J］．岩土工程学报，1996，18（1）：95-97．

［5］沈珠江．结构性粘土的弹塑性损伤模型［J］．岩土工程学报，1993，15（3）：21-28．

［6］刘恩龙，沈珠江．结构性土的二元介质模型［J］．水利学报，2005，36（4）：391-395．

［7］DESAI C S．Mechanics of Materials and Interfaces：The Disturbed State Concept［M］．Boca Raton：CRC Press，2001．

［8］LIU M D，CARTER J P．Modelling the Destructuring of Soils during Virgin Compression［J］．Geotechnique，2000，50（4）：479-483．

［9］ YIN Z，KARSTUNEN M，CHANG C S，et al．Modeling Time-dependent Behavior of Soft Sensitive Clay［J］．Journal of Geotechnical and Geoenvironmental Engineering，2011，137（11）：1103-1113．

［10］BUTTERFIELD R．A Natural Compression Law for Soils （An Advance on e-logp＇）［J］．Géotechnique，1979，29（4）：469-480．

［11］ CHAI J，MIURA N，ZHU H，et al．Compression and Consolidation Characteristics of Structured Natural Clay ［J］．Canadian Geotechnical Journal，2004，41（6）：1250-1258．

［12］LOW H，PHOON K，TAN T，et al．Effect of Soil Microstructure on the Compressibility of Natural Singapore Marine Clay［J］．Canadian Geotechnical Journal，2008，45（2）：161-176．

［13］JUNG Y，FINNO R J，CHO W．Stress-strain Responses of Reconstituted and Natural Compressible Chicago Glacial clay［J］．Engineering Geology，2012，129（1）：9-19．

［14］BJERRUM L．Engineering Geology of Norwegian Normally-consolidated Marine Clays as Related to Settlements of Buildings［J］．Geotechnique，1967，17（2）：83-118．

［15］JIA R．Consolidation Behavior of Ariake Clay under Constant Rate of Strain［D］．Saga，Japan：Saga University，2010．

［16］LEROUEIL S，KABBAJ M，TAVENAS F．Study of the Validity of aModel in In situ Conditions［J］．Soils and Foundations，1988，28（3）：13-25．

［17］LEROUEIL S，KABBAJ M，TAVENAS F，et al．Stressstrain-strain Rate Relation for the Compressibility of Sen-sitive Natural Clays［J］．Geotechnique，1985，35（2）：159-180．

［18］SMITH P R，JARDINE R J，HIGHT D W．The Yielding of Bothkennar Clay［J］．Géotechnique，1992，42（2）：257-274．

［19］LIU M D，CARTER J P．Virgin Compression of Structured Soils［J］．Géotechnique，1999，49（1）：43-57．

［20］ISLAM M K，CARTER J P，SIDDIQUEE M，et al．A Method for Derivation of Compression Equation and Value ofDegradationExponentforStructuredSoils［J］．Geotechnical and Geological Engineering，2013，31（5）：1587-1601．

［21］MESRI G，ROKHSAR A，BOHOR B F．Composition and Compressibility of Typical Samples of Mexico City Clay ［J］．Geotechnique，1975，25（3）：527-554．

［22］PERRET D，LOCAT J，LEROUEIL S．Strength Development with Burial in Fine-grained Sediments from the Saguenay Fjord，Quebec［J］．Canadian Geotechnical Journal，1995，32（2）：247-262．

［23］TANAKA H，LOCAT J，SHIBUYA S，et al．Characterization of Singapore，Bangkok，and Ariake Clays［J］．Canadian Geotechnical Journal，2001，38（2）：378-400．

［24］曾玲玲，洪振舜，刘松玉，等．天然沉积结构性土的次固结变形预测方法［J］．岩土力学，2011，32（10）：3136-3142．

［25］DEN HAAN E J．The Formulation of Virgin Compression of Soils［J］．Géotechnique，1992，42（3）：465-483．

（编辑：陈敏）

Mathematical Description of One-dimensional Compression Behaviour of Structured Soft Clays

KE Wen-hui1，2，CHEN Jian1，SHENG Qian1，FANG Qiang1，BIAN Xiao-man1，ZHAO Qing1
（1．State Key Laboratory of Geomechanics and Geotechnical Engineering，Institute of Rock and Soil Mechanics，Chinese Academy of Sciences，Wuhan430071，China；2．Wuhan Municipal Construction Group Co．，Ltd．，Wuhan430023，China）

In order to explore the effect of structure on one-dimensional compression deformation of soft clays，we described the characteristics of structural failure under one-dimensional compression firstly．On this basis，the relationship between compression index and void ratio was revealed and a new mode that describes the progressive destructuration during the 1D compression was proposed．Secondly，the formula of the virgin compression curve of structured soft clays is deduced based on the above proposed descriptive mode and the effects of structural parameters on the virgin compression curves are analyzed．Thirdly，the experimental data of 10 representative structured clays from literatures together with the results of conventional oedometer tests on Ningbo clay are used to verify the proposed descriptive mode's validity．Furthermore，a comparative analysis on the simulated results of 1D compression curves for Mexico City clays is made between the proposed descriptive mode and other 6 common descriptive modes．Finally，the variation regularity of structural parameters with the difference between nature water content and plastic limit is discussed and then the empirical formulas of structural parameters are established by the linear regression method．The results show that the proposed descriptive mode characterizes the compression destructural behavior of structured soft clays under 1D loading condition accurately．This research provides theoretical basis for establishing constitutive models of natural structured soft clays，and also offers a new idea for further study on compression deformation behavior．

soft clay；structural property of soil；destructuration；compression behavior；mathematical description；virgin compression curves；structural parameter

TU433

A

1001-5485（2016）07-0087-06

2015-04-17；

2015-05-20

国家自然科学基金重大研究计划集成项目（91215301）；国家重点基础研究发展计划973项目（2015CB057905）；中国科学院重点部署项目、百人计划项目（NKZZDEWTZ12）

柯文汇（1987-），男，湖北黄石人，博士研究生，主要从事软土工程特性及软土地下工程变形机理研究，（电话）027-85890201（电子信箱）kewenhui1989@126．com。

陈健（1972-），男，江西九江人，研究员，博士，从事城市地下工程与地下空间安全评价与风险分析方面研究，（电话）027-87198175（电子信箱）jchen@whrsm．ac．cn。