基于蚁群算法的冻结重塑黏土分数阶导数西原模型分析

姚兆明，张秋瑾，牛连僧



基于蚁群算法的冻结重塑黏土分数阶导数西原模型分析

姚兆明1，张秋瑾1，牛连僧2

（1．安徽理工大学土木建筑学院，安徽淮南232001；2．黄冈师范学院建筑学院，湖北黄冈438000）

掌握冻结状态下岩土体的蠕变规律，对利用冻结法施工的井筒建设安全至关重要。对人工冻结重塑黏土在-5，-10，-15℃下进行单轴抗压强度试验，得到温度对人工冻结重塑黏土单轴抗压强度的影响规律；根据重塑黏土冻结下的单轴强度，分别进行3个加载等级的蠕变试验，得到温度、加载等级对蠕变的影响规律。将Abel黏壶引入到西原模型，建立分数阶导数西原模型；利用蚁群算法对重塑黏土冻结状态下蠕变西原模型和分数阶西原模型进行参数辨识，通过分析2种模型的模拟结果，表明分数阶西原模型更适合于计算重塑黏土冻结状态下的蠕变规律。

冻结重塑黏土；蠕变；蚁群算法；分数阶导数；西原模型

doi：10．11988/ckyyb．20150419

1　研究背景

深厚表土井筒建设工程中，冻结壁处于复杂的高应力状态，由冻土蠕变引起大的蠕变变形可能引起冻结管断裂甚至引发严重的安全事故。因此，研究冻土的蠕变变形规律具有非常重要的意义。计算岩土体蠕变的模型有经验模型［1-2］、元件模型［3-5］。经验模型参数由最小二乘法通过误差传递得到，所得到的模型参数不具有明确的物理意义；组成元件模型有整数阶元件和分数阶元件，整数阶元件如虎克体、牛顿体及刚-塑体，由不同整数阶元件组合而成的有伯格斯模型、开尔文模型、西原模型等，整数阶模型具有严格的力学推导、理论性强且模型参数物理意义明确［3］。

固体颗粒、液相水、冰和气组成冻结状态下的重塑黏土［6］，其蠕变特性既不能用黏性定律，也不能用弹性定律来描述，只能用介于弹性和黏性的规律来解释。如用整数阶元件组合模型进行计算，将需要多个整数阶元件进行复杂的组合才能达到满意的结果；任意阶次的元件模型可以通过分数导数来构建［7-9］。整数阶元件模型具有的优点不仅能在分数阶导数元件模型中得到体现，而且需要多元件复杂组合才能计算重塑黏土冻结状态下蠕变的不足，能通过分数阶导数元件模型来克服。

本构模型参数辨识是人工冻土理论与工程实践中的重要研究课题，国内外学者在此领域做了大量的工作［10-11］。参数辨识的基本思路是依据蠕变实验数据，通过遗传算法、蚁群算法、粒子群算法等来优化蠕变模型中的参数［12-13］。蚁群算法是一种解决复杂问题有独特优势的仿生优化算法［14］，本文用蚁群算法来优化本构模型，提出了分数阶导数模型确定参数的新方法。

2　重塑黏土冻结状态试验

2．1重塑黏土单轴抗压强度试验

土样为黏土，含水率为22%，干重度γd为17．2 kN/m3。试样的尺寸为50 mm（直径）×100 mm（高度）的标准试样，见图1。力-应变曲线能实时显示，仪器如图2所示。不同温度冻结状态下重塑黏土单轴抗压试验结果见表1。

图1　试验前后试样Fig．1　Soil specimens before and after test WDT-100型人工冻土试验仪器由计算机控制，试验过程中的荷载及应变能实时采集并查询，应

图2WDT-100冻土试验机Fig．2　WTD-100 testing machine for artificial frozen soil

表1　不同温度重塑黏土单轴抗压强度Table 1　Test results of uniaxial compressive strength for artificial frozen soil under different temperatures

分析重塑黏土冻结状态下的抗压强度与冻结温度的关系规律，两者具有很好的线性关系。抗压强度随着冻结温度的降低而增大。重塑黏土冻结状态下破坏形态大多呈塑性破坏（见图1（b））。不同试验温度下的冻土试样轴向应力-应变与时间的关系曲线见图3。

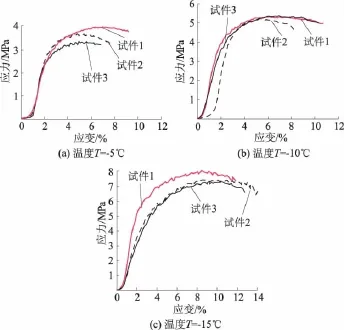
图3　冻土试样在不同温度下的应力-应变关系曲线Fig．3　Stress-strain curves of frozen soil samplesunder different temperatures

2．2单轴蠕变试验

蠕变试验分别在-5，-10，-15℃3个温度水平下进行。试验加载按照0．3σ0，0．5σ0，0．7σ03个加载等级进行，σ0为单轴强度。3种加载应力见表2，蠕变试验试样的前后对比效果见图4。蠕变曲线见图5、图6。

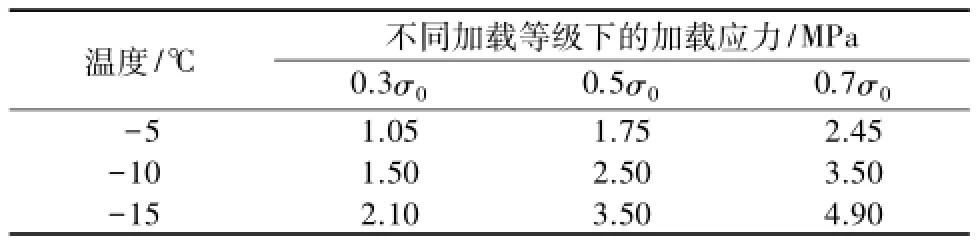
表2　重塑黏土冻结状态下蠕变试验加载应力Table 2　Loading stress of creep test for artificial frozen soil

图4　黏土的蠕变破坏形态Fig．4　Failure pattern of clay in creep test

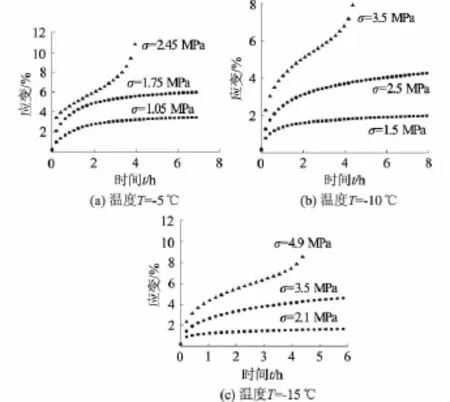
图5　不同温度下的人工冻土蠕变试验曲线Fig．5　Creep curves of artificial frozen clay under different temperatures

从图5可以看出，当温度相同时，冻土蠕变从初始蠕变阶段转入常应变蠕变阶段时间几乎一致，均在1．5 h内完成，可见加载系数对其影响较小。但是加载系数对稳定蠕变值的影响较大。-5℃时0．3和0．5加载系数下的稳定蠕变值分别为3．06%和5．89%，蠕变值提升达92%；-10℃时，2种加载系数下的稳定蠕变值分别为1．98%和4．26%，蠕变值提升达115%。

从图6可以看出，当加载系数相同时，冻结重塑黏土从初始蠕变阶段发展到常应变蠕变阶段的时间随温度的降低而逐渐提前。同时随着温度的降低，冻结试样达到稳定蠕变值也相应的降低。如当加载系数为0．3时，-5，-10，-15℃3个温度达到稳定的蠕变值分别为3．46%，1．98%，1．65%。

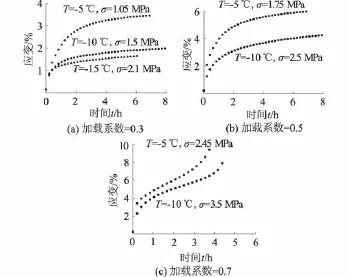
图6　不同加载系数下的人工冻土蠕变曲线Fig．6　Creep curves of artificial frozen clay underdifferent loading coefficients

3　冻土的分数阶导数西原蠕变模型

3．1西原模型

西原模型虎克体、牛顿黏壶和摩擦件以一定的组合形成，见图7。西原模型常用来描述软土和软岩的蠕变规律。

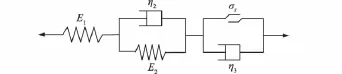
图7 西原模型Fig．7　Nishihara model

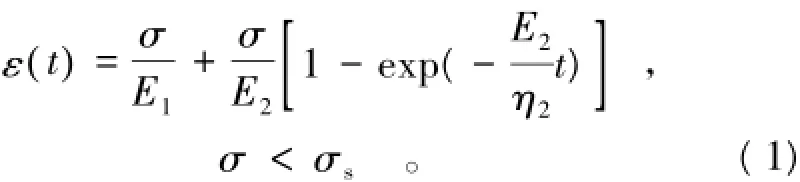
稳态的西原模型的本构方程为ε（ t ）=σ+σ［1-exp（-E2t）］+σ-σst，

E1E2η2η3σ≥σs。（2）式中：σ为蠕变试验加载值；ε（t）为应变；η2，η3均为重塑黏土冻结状态下的黏滞参数；E1，E2均为重塑黏土冻结状态下的弹性参数；σs为重塑黏土冻结状态下蠕变的应力阀值；t为时间。

3．2分数阶导数的西原模型

3．2．1分数阶导数元件模型

式（3）为Abel黏壶的本构方程［7］，元件见图8。

加速的西原模型的本构方程为

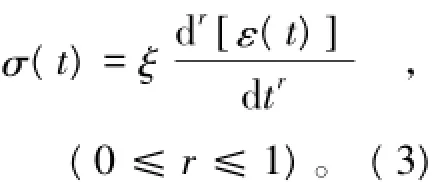
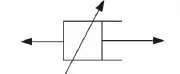
图8　Abel体Fig．8　Abel dashpot

3．2．2分数导数西原模型

图9为分数阶导数西原蠕变模型。

式中ξ为Abel黏壶的黏性系数。当r=0时，Abel黏壶为弹簧元件，表示理想弹性体；当r=1时，Abel黏壶即为牛顿黏壶，表示理想流体。由此可见，介于理想流体与理想弹性冻结状态下重塑黏土的蠕变特性可以用常系数Abel黏壶来模拟。

应力不变，即σ（t）为常数时，材料的蠕变特性能用Abel黏壶元件模型描述，对式（3）进行分数阶积分，分数阶导数元件蠕变方程由Riemann-liouville型积分算子理论得到［7］，即

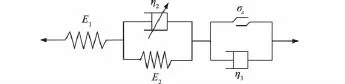
图9　分数阶导数西原模型Fig．9　Nishihara model with fractional order derivative

分数阶导数稳态西原模型人工冻土蠕变模型的本构方程为

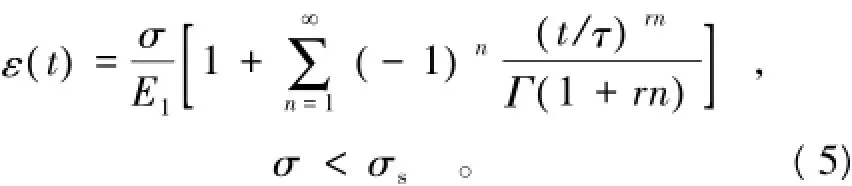
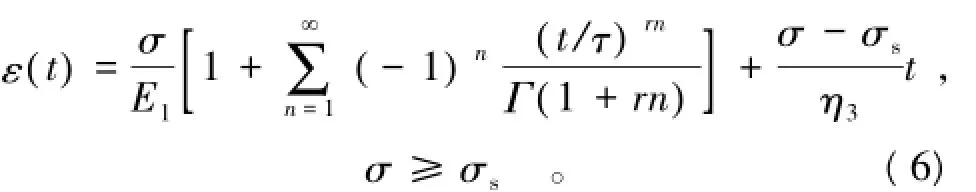
3．3蚁群算法优化模型参数

意大利学者M．Dorigo等于20世纪90年代初提出蚁群算法［15］。蚁群算法是一种群体智能算法，具有很好的鲁棒性、正反馈特性及且并行搜索特点。

确定蠕变模型参数是组合优化问题，根据参数的组合来建立目标函数，然后运用蚁群优化算法对最优的目标函数值进行搜索，得到合适的组合参数取值。

通过蚁群优化算法优化蠕变模型的参数。具体算法步骤如下所述［16］。

3．3．1参数初始化

（1）随机分配每只蚂蚁一组蠕变模型参数，即

分数阶导数加速的西原模型人工冻土蠕变模型的本构方程为

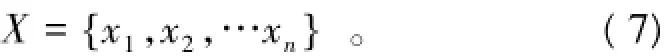
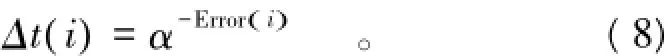
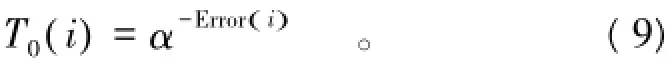
由式（9）可知，误差值越小，信息素越大。

3．3．2保存每代全局最优解

（1）每个蚂蚁下一步转移概率由蚂蚁留下的信息素大小确定，即

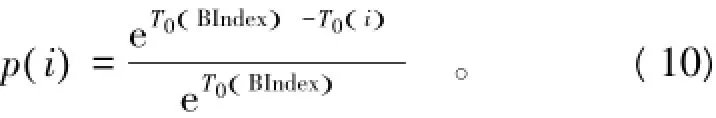
式中：α为基本参数；Error为误差指数。

（3）初始化蚁群算法中的信息素，即蚂蚁i位置的信息素由误差值来确定，即

式中BIndex为信息素最大的蚂蚁。

（2）动态挥发因子构建：为得到全局最优解，较小的信息素在开始阶段得以挥发，随着不断增加进化次数，信息素挥发因子逐渐增大。定义信息素挥发因子为

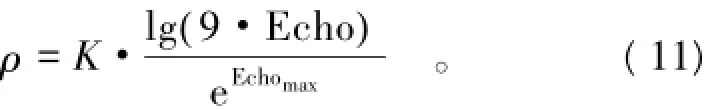
式中：K=0．1；Echo表示蚁群当前的进化代数；Echomax表示蚁群的最大进化代数。

（3）动态转移因子确定：迭代过程时，信息素大小确定全局转移因子p0。设m为蚂蚁的数量，计算，升序排序计算结果，得到序列当Echo＜（Echomax/2）时，

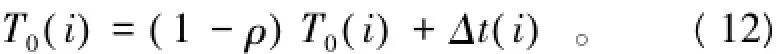
（5）保存最优代：迭代过程中，将信息素最大的蚂蚁保存下来，误差值由误差模型计算，返回参数初始化步骤，进行迭代循环。

（6）最优解全局优化：迭代次数达到初始设置值时，结束搜索。蠕变模型参数由最佳蚂蚁转换而成。

3．4人工冻土单轴蠕变分数阶导数模型

3．4．1西原蠕变模型

利用蚁群算法对西原模型参数进行优化，模型参数见表3。西原模型计算值与试验值对比见图10。

局部搜索在转移概率＜p0时进行；全局搜索当转移概率＞p0时进行。为得到更好的解，局部搜索在开始阶段进行；为避免陷入局部最优全局搜索在后期阶段进行。

（4）更新模型参数信息素：利用式（12）对蠕变模型参数进行信息素更新，即

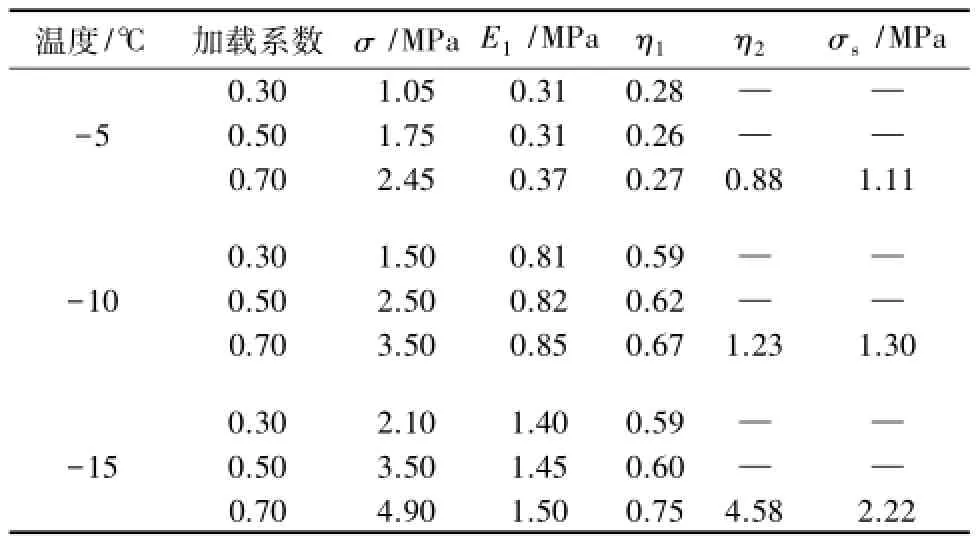
表3　黏土西原蠕变模型参数Table 3　Creep parameters in Nishiara model

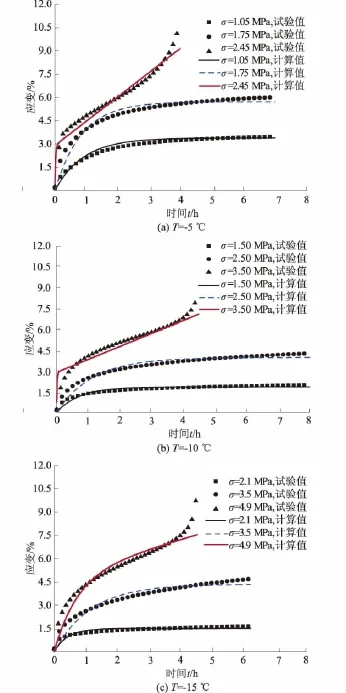
图10　经典西原模型的计算值与单轴蠕变试验值对比（黏土）Fig．10　Comparison between calculated value in Nishihara model and tested value by uniaxial creep test

通过对经典的西原模型的计算值与试验值的对比中可以得出以下结论：模拟曲线对于冻土的初期蠕变阶段、稳定蠕变阶段吻合较好，基本上能够反映冻土的蠕变变趋势，但是对于冻土的加速蠕变阶段，误差很大，可见，经典的西原模型描述冻土的加速蠕变阶段的蠕变变形是有误差的。

3．4．2分数阶导数西原模型

利用蚁群算法对分数阶导数西原模型计算结果见图11。分数阶导数西原模型的参数进行优化，模型参数见表4。

由图11可见，蚁群算法能有效优化分数阶导数西原模型参数；分数阶导数西原模型很好地反映重塑黏土冻结状态下的蠕变发展规律。

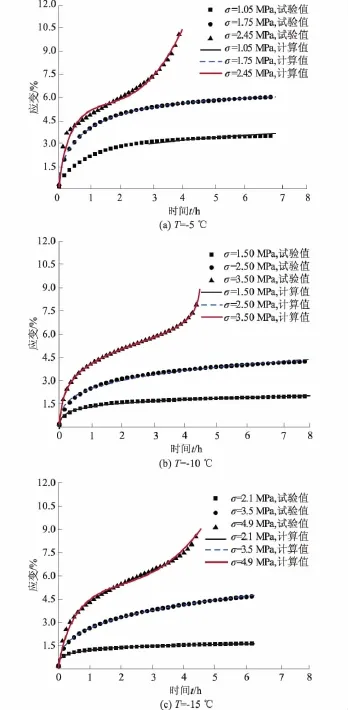
图11　分数阶导数西原模型计算值与试验值对比Fig．11　Comparison between calculated value by Nishihara model with fractional order derivative and test values

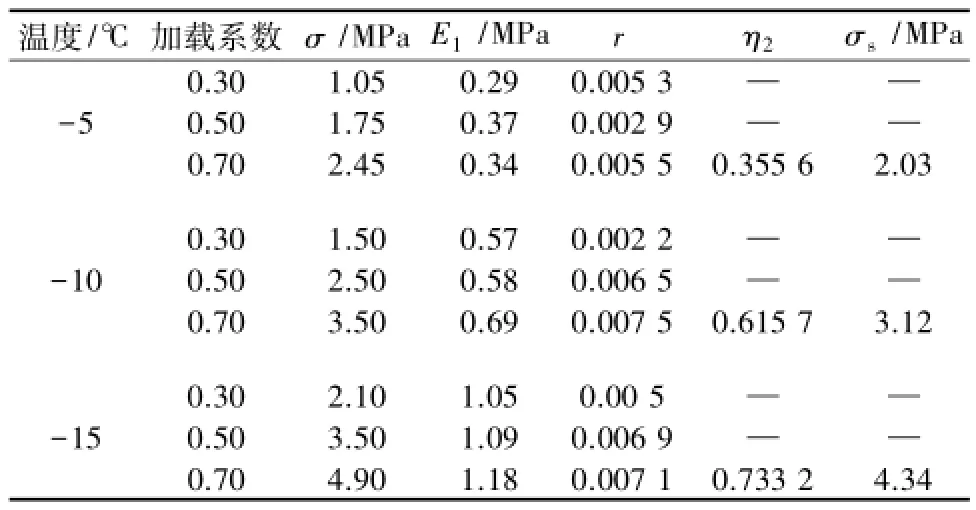
表4　黏土粒子群分数阶导数西原蠕变模型参数Table 4　Creep parameters of fractional order derivative Nishihara model improved by particle swarm algorithm

4结论

（1）重塑黏土冻结状态下单轴抗压强度与温度呈线性关系，随着冻土冻结温度的降低，重塑黏土冻结状态下的抗压强度强度增大；重塑黏土冻结状态下破坏形态呈塑性破坏。

（2）加载系数相同时，冻结重塑黏土从初始蠕变阶段发展到常应变蠕变阶段的时间随温度的降低而逐渐推迟；冻结试样达到稳定蠕变值随温度的降低而降低；相同冻结温度下，冻结重塑黏土蠕变从初始蠕变阶段发展到常应变蠕变阶段时间变化不大，加载系数对其基本不产生影响；稳定蠕变值受加载系数影响较大。

（3）蚁群算法作为一种解决复杂问题有独特优势的仿生优化算法，能有效优化分数阶导数西原模型参数；分数阶导数西原模型很好地反映重塑黏土冻结状态下的蠕变发展规律。

［1］ 王松鹤，骆亚生．黄土三轴剪切蠕变特性研究［J］．岩土工程学报，2010，32（10）：1633-1637．

［2］王者超，Ron Wong，乔丽苹．油砂的蠕变特性与本构模型研究［J］．岩土工程学报，2012，34（8）：1412-1423．

［3］齐亚静，姜清辉，王志俭，等．改进西原模型的三维蠕变本构方程及其参数辨识［J］．岩石力学与工程学报，2012，31（2）：347-355．

［4］王元战，黄东旭，肖忠．天津滨海地区两种典型软黏土蠕变特性试验研究［J］．岩土工程学报，2012，34（2）：379-384．

［5］高春艳，高全臣，江斌等．朱集煤矿泥岩的流变试验与本构模型研究［J］．长江科学院院报，2015，32（5）：76-81．

［6］ 齐吉琳，马巍．冻土的力学性质及研究现状［J］．岩土力学，2010，31（11）：133-143．

［7］殷德顺，和成亮，陈文．岩土应变硬化指数理论及其分数阶微积分理论基础［J］．岩土工程学报，2010，32（5）：762-766．

［8］陈军浩，姚兆明，徐颖，等．人工冻土蠕变特性粒子群分数阶导数模型［J］．煤炭学报，2013，38（10）：1763-1768．

［9］姚兆明，周洋，徐颖，等．人工冻土遗传分数阶导数加速伯格斯蠕变模型［J］．工业建筑，2013，43（11）：73-76．

［10］张强勇，陈芳，杨文东，等．大岗山坝区岩体现场剪切蠕变试验及参数反演［J］．岩土力学，2011，32（9）：2584-2590，2602．

［11］蒋海飞，胡斌，刘强，等．一种新的岩石黏弹塑性流变模型［J］．长江科学院院报，2014，31（7）：44-48．

［12］周伟，常晓林，胡颖，等．基于改进遗传算法的堆石体流变模型参数反馈分析［J］．水力水电学报，2007，26（3）：29-33．

［13］FENG Xia-ting，CHEN Bing-rui，YANG Cheng-xiang，et al．Identification of Visco-elastic Models for Rocks Using Genetic Programming Coupled with the Modified Particle Swarm Optimization Algorithm［J］．International Journal of Rock Mechanics&Mining Sciences，2006，43（3）：789-801．

［14］高玮．基于蚁群聚类算法的岩爆预测研究［J］．岩土工程学报，2010，32（6）：874-879．

［15］DORIGO M，GAMBARDELLA L M Ant Colonies for the Travelling Salesman Problem［J］．Biosystems，1997，43（2）：73-81．

［16］庄严，白振林，许云峰．基于蚁群算法的支持向量机参数选择方法研究［J］．计算机仿真，2011，28（5）：216-219．

（编辑：姜小兰）

Analysis of Fractional Order Derivative Nishihara Model of Frozen Remolded Clay Based on Ant Colony Algorithm

YAO Zhao-ming1，ZHANG Qiu-jin1，NIU Lian-seng2
（1．School of Civil Engineering and Architecture，Anhui University of Science and Technology，Huainan 232001，China；2．School of Architecture，Huanggang Normal University，Huanggang438000，China）

It is of great significance to master the creep law of rock-soil body under frozen state for the safe shaft construction by using freezing method．We carry out uniaxial compressive strength tests for artificial freezing remolded clay at the temperature of-5℃，-10℃ ，-15℃，respectively．Furthermore，we obtain the relationship between temperature and uniaxial compressive strength of artificial freezing remolded clay．According to uniaxial strength under frozen state of remolded clay，we conduct creep test with 3 loading levels and obtain the influence of temperature and loading level on creep．Furthermore，we introduce Abel dashpot into Nishihara model and establish fractional order derivative Nishihara model．Finally，by introducing ant colony algorithm into frozen remolded clay，we finish parameter identification for Nishihara creep model and fractional order derivative Nishihara model．Through analyzing simulated results in two models，we can find that fractional order derivative Nishihara model is more appropriate than creep Nishihara model in creep calculation for frozen remolded clay．

frozen remolded clay；creep；ant colony algorithm；fractional order derivative；Nishihara model

TU443

A

1001-5485（2016）07-0081-06

2015-05-20；

2015-07-03

国家自然科学基金项目（40972188）

姚兆明（1975-），男，安徽黄山人，教授，博士后，主要从事土体本构理论和岩土数值分析研究，（电话）0554-6668532（电子信箱）zhmyaoaust@126．com。