一种改进的Memetic差分进化算法

甘肃政法学院 赵进龙兰州理工大学 霍明明



一种改进的Memetic差分进化算法

甘肃政法学院 赵进龙
兰州理工大学 霍明明

【摘要】提出一种改进的自适应memetic差分进化算法，通过引入正态分布的概念，在种群初始化和局部搜索方面对经典差分进化算法进行改进，提高其寻优精度。并通过引入自适应算子，在增强算法全局收敛性的同时又保证算法具有较高的收敛速度。实验仿真结果表明，改算法具有较好的全局收敛性并能有效避免早熟收敛。

【关键词】差分进化算法；Memetic算法；自适应

1　引言

遗传算法是一类借鉴生物界自然选择和自然遗传机制的随机优化算法，因其原理简单，鲁棒性强，适于并行计算等优点，自1975 年J.Holland［1］教授提出之日起，对遗传算法的研究如火如荼。但是遗传算法采用二进制编码，这种编码方式的最大缺点就是长度较大，对很多优化问题来说用其他的编码方式可能更有利。差分进化算法（Differential Evolution algorithm）是1995年Storn等人［2］为解决切比雪夫多项式问题时提出的。差分进化算法是基于群体智能理论的优化算法，相比于遗传算法，DE继承了基于种群的全局搜索策略，采用浮点数编码和基于差分的简单变异操作以及贪婪的竞争生存策略，降低了算法的复杂度。DE独有的记忆功能使其可以根据当前搜索情况，动态调整搜索策略，具有较强的鲁棒性和全局搜索能力。

全局搜索和局部开发能力的平衡是提高差分进化算法搜索性能的关键性问题，而这在较大程度上依赖于算法中控制参数（NP，F，CR）的选取。陈岩等［3］通过个体间距离、个体适应度等指标来增强种群的多样性。2006年，Brest J等［4］提出了一种JDE算法，对F，CR进行自适应调整。针对DE易过早收敛和陷入局部最优甚至停滞的现象［5-6］，郭义波等［7］提出了随机选择变异策略、自适应调整交叉率和自适应调整变异率的设想，达到了局部搜索和全局搜索的平衡。谭跃等［8］提出了一种混沌局部搜索策略的差分进化算法（CLSDE），在最优个体附近利用混沌算法进行局部搜索，使算法跳出局部最优。

Memetic算法［9］继承了遗传算法全局搜索能力强的特点，同时Memetic中的局部搜索策略又弥补了遗传算法局部搜索能力差的缺点，达到了全局搜索和局部搜索的平衡。本文一改标准差分进化算法随机初始化种群带来的弊端，对种群初始化算法进行改进，并加入自适应算子对种群进行动态调节，引入memetic算法达到全局搜索和局部搜索的平衡。

2　经典差分进化算法

经典差分进化算法的数学描述如下：

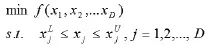
图1　差分进化算法的流程图

3　改进的差分进化算法

差分进化算法最优解的质量取决于初始群体是否能包含解空间内的全部可能的解，并且保证在进化过程中不失去其中的优良个体。由此可见初始种群既不能粗略的随机产生，也不能遍历所有状况，尤其对于多变量问题，只要将解空间中最具有代表性的个体作为初始种群，才能更好的反映解空间的内在特征。

标准的差分进化算法采用随机方法产生初始种群，这种方法在一定程度上影响了算法的寻优能力和收敛速度，而利用服从正态分布的方法产生初始种群，且每次产生一个个体，这种方法在一定程度上增加了最优解被选择的可能性，提高了算法的寻优能力。其公式如下：

其中，randn（1）产生服从N（0，1）的随机数。

服从N（0，1）分布的种群个体分布图如图2所示：

图2　服从正态分布的初始种群分布图

3.2自适应算子

缩放因子F在一定程度上控制了种群进化的方向，对算法的全局搜索和局部搜索能力起到了一定的程度的调节作用。F较小，有利于提高收敛速度和增强局部搜索能力，但种群多样性较低，容易出现早熟和局部最优；F较大，有利于算法的全局搜索和保持种群的多样性，但局部搜索能力较低。高岳林等［10］认为F的值既不能太大，也不能小于某一特定值，建议之间时，算法能得到较好的结果。

Amin Nobakhti等［11］认为CR越大，试验矢量每一维选择变异矢量的概率越大，从而使试验矢量相对于目标矢量受到更大的扰动（perturbation），降低了算法的收敛速度；反之，小的CR将快速失去种群的多样性（rapid loss of diversity）。

图5(a)、5(b)和5(c)分别为旋流器内x=0平面三条特征线Z-1、Z-2和Z-3上的切向速度分布图。

综上，本文提出了如下自适应的缩放因子和交叉概率因子：

其中，G表示迭代次数，Gmax代表最大迭代次数。

3.3局部搜索策略

局部搜索是Memetic算法中一个最重要的环节，同时也是差分进化算法能否得到最优解的决定因素之一。对于一个较好的算法，要能在算法的前期具有较强的全局搜索能力，使算法最终能收敛到解空间中的最优解；算法后期具有较强的局部搜索能力，以提高算法的收敛速度和搜索精度。

局部搜索策略是一种近似算法，一般能给出一个可以接受的较好的解，但有可能陷入局部峰值，算法就在该点结束，此时得到的结果有可能就是一个较不理想的结果。本文采用在每次迭代结束后，以概率P从邻域中随机选择一个个体，并在该个体附近进行k局部搜索，得到最优解xbest，若xbest优于xbest，则用xbest的值取代xbest的值，并xbest随机取代种群中的一个个体，结束本次搜索，否则继续DE的基本操作。局部搜索公式如下：

xbest=xrand+Normalrand（0，1） （5）

其中，Normalrand（0，1）服从期望为0，方差为1的标准正态分布。

随着迭代次数的增加，种群多样性的降低是导致种群出现早熟的根本原因。为判断种群是否出现停滞或达到最优解，本文引入聚集度因子（aggregation degree factor）A。

4　数值试验

为验证本文提出的改进算法IMDE的有效性，选择四个benchmarks函数中经典的4个测试函数：Griewank、Schwefel、Rosenbrock、Rastrigin。测试函数的相关描述见表1。对于上述4个测试函数，文中选用DE / rand / 1 / bin进行寻优测试，以比较DE和IMDE的性能。测试环境：matlab R2010b。

关于实验参数设置，除f1函数的最大迭代次数为1000，种群规模为NP=60，f4的阈值为100外，其他函数参数设置为：局部搜索次数k=20，种群规模NP=100，最大迭代次数ITER=2000，阈值=0.15，选择概率P=0.75。得到如表2所示结果。

表1　典型Benchmarks函数描述

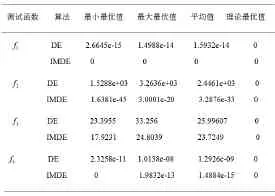
表2　Benchmarks函数测试寻优结果

从表2和图3中可以看出，本文提出的IMDE算法对f1～f4的寻优结果都优于标准DE算法，其中对于f1函数，本文提出的IMDE算法可以找到其全局最优值（注：图3中f1函数寻优对比图像中未出现红线，说明在算法的第一次迭代中就找到了最优解）。

图3　f1～f4的寻优对比曲线

从以上仿真对比结果可以看出，IMDE的寻优能力要优于标准DE，证明本文提出的IMDE算法对求解优化问题更有效。

5　结论

本文在分析了标准差分进化算法存在的优点和缺点的基础上，提出了一种服从标准正态分布的初始化方法，提高了算法寻优效率和寻优精度。利用Memetic算法强大的局部搜索能力，将Memetic算法和DE算法相结合，实现了IMDE算法全局搜索和局部搜索的平衡，并加入自适应算子对种群进行自适应调整，提高了算法的收敛速度。实验表明，本文提出的IMDE算法对求解优化问题的有效性。

参考文献

［1］Holland J H.Adaption in natural and artificial systems［M］.The University of Michigan Press，975：1-50.

［2］Storn R，Price K.Differential evolution：a simple and efficient heuristic for global optimization over continuous spaces［J］.Journal of G local Optimization，1997，11（4）：341-359.

［3］陈岩，王宗宪.基于多准则寻优策略的差分进化算法研究法［J］.山东科技大学学报（自然科学版），2016，35（1）：102-108.

［4］Brest J，Greiner S，Boskovic B，et al.S elf adapting control parameters in diff- erential evolution：a comparative study on numerical benchmark problems［J］.Journal of IEEE Trans Evolutionary Computation ，2006，10（6）：646-657.

［5］Holland J H.Adaptation in natural and artificial systems［M］.Ann Arbor：Michigan Press，1975：1-50.

［6］Yang Q W，Jiang J P，Qu Z X，et al.Improving genetic algorithms by using logic operation［J］.Control and Decision，2002，15（4）：520-512.

［7］郭义波，程际云，李芹，杨平.随机选择变异及自适应差分进化算法的研究［J］.上海电力学院学报，2016，32（2）：162-174.

［8］谭跃，谭冠政.混沌局部搜索策略的差分进化算法［J］.重庆工学院学报，2009，23（5）：64-70.

［9］Peter Merz，Bernd Freisleben.Memetic Algorithms and the Fitness Landscape of the Graph Bi Partitioning Problem.PPSN VLNCS 1998：765-774.

［10］高岳林，刘军民.差分进化算法的参数研究［J］.黑龙江大学自然科学学报，2009，26（1）：81-85.

［11］Amin Nobakhti，Hong Wang.A simple self-adaptive differential evolution algorithm with application on the ALSTOM gasifier［J］.Applied Soft Computing，2008，8：350-370.

作者简介：

赵进龙（1985—），河北石家庄人，硕士，助教，主要研究方向：算法设计与分析。

霍明明（1986—），河南开封人，硕士，助教，主要研究方向：算法设计与分析。