基于准同步Prony的谐波和间谐波检测算法

中国矿业大学（徐州） 山东能源枣矿集团供电工程处 张 浩



基于准同步Prony的谐波和间谐波检测算法

中国矿业大学（徐州） 山东能源枣矿集团供电工程处 张 浩

【摘要】针对传统傅里叶变换在非同步采样条件下存在频谱泄露，以及谐波和间谐波在分析过程中相互之间存在干扰的问题，本文创新性地提出一种基于准同步-梳状滤波器分离-Prony谱分析算法（QS-Prony）。该算法首先使用基于频移算法的准同步采样技术，通过构造同步采样序列，实现非同步采样信号的准同步化。为了避免信号中谐波、间谐波之间的互扰问题，对频移后的准同步序列使用梳状FIR陷波型滤波器近一步分离。随后采用Prony谱分析法，使用指数函数的线性组合来拟合采样数据，并提取信号的频率、幅值、相位等特征量。在不同强度的噪声干扰环境下对比验证了加窗插值FFT算法（WI-FFT）、准同步-梳状滤波器分离-加窗插值FFT算法（QS-WI-FFT）、准同步-梳状滤波器分离-Prony谱分析算法（QS-Prony）的准确度。实验结果表明QS-Prony法可以有效解决非同步问题，有效避免了谐波、间谐波之间的互扰，并且相比FFT算法具有较高的频率分辨率。

【关键词】谐波；间谐波；Prony算法；梳状滤波器；Matlab

0　引言

当今社会越来越多的高科技设备采用新工艺，新技术，其对电源的敏感性也越来越高，因此社会对于电能质量的要求也越发的提高。但与此同时，随着大量电力电子设备投入到电力系统中，其所具有的负荷非线性、非对称性、冲击性等特性向电力系统注入各种电磁干扰，对电力系统的电能质量和用户设备的安全运行造成不良影响，甚至引发严重的安全生产事故。

目前谐波、间谐波的分析方法主要有傅里叶变换［1］，小波变换，基于瞬时无功功率理论的检测法，现代谱估计法。快速傅里叶变换（ fast fourier transformation，FFT）由于其简单、快速的优点，但是信号基频变化导致非同步采样时，会存在严重的频谱泄露问题，影响谐波测量的准确性［2］；小波变换有较高的时频分辨率，在波动快速、频繁的谐波检测方面具有较大优势，但对噪声敏感［3-4］；基于瞬时无功功率理论的检测法在进行电流检测时，不受电网波动的影响，检测几乎无延时，实时性很好，但由于该技术是针对电力有源滤波器开发出来的，因此它仅需或仅能得到三相电路的总谐波电流含量。现代谱估计法是一种新兴的谐波检测算法。现代谱估计算法的优点是：对有限的窄带信号没有频率分辨率的限制，可以分析无限小频率间隔的相邻两频率成分。Prony算法将非线性问题转化为了线性问题，具有更好的频率分辨率，对于间谐波的分析具有广阔的应用前景。

针对传统傅里叶变换在非同步采样条件下存在频谱泄露，以及谐波和间谐波在分析过程中相互之间存在干扰的问题，创新性地提出一种基于准同步-梳状滤波器分离-Prony谱分析算法（QSProny）。该算法首先使用基于频移算法的准同步采样技术，通过构造同步采样序列，实现非同步采样信号的准同步化。为了避免信号中谐波、间谐波之间的互扰问题，对频移后的准同步序列使用梳状FIR陷波型滤波器近一步分离。随后采用Prony谱分析法，使用指数函数的线性组合来拟合采样数据，并提取信号的频率、幅值、相位等特征量。在不同强度的噪声干扰环境下对比验证了加窗插值FFT算法（WI-FFT）、准同步-梳状滤波器分离-加窗插值FFT算法（QS-WI-FFT）、准同步-梳状滤波器分离-Prony谱分析算法（QSProny）的准确度。

本文通过实验结果验证表明QS-Prony法可以有效解决非同步问题，有效避免了谐波、间谐波之间的互扰，并且相比FFT算法具有较高的频率分辨率。

1　基于频移的准同步方法

假设谐波信号模型为：

式中：f0是基波频率，A0是幅值，是初相位。

进一步应用DFT求取x（n）频谱时，相当于在频域范围内对等间隔抽样N点，则峰值对应的频率fm为：

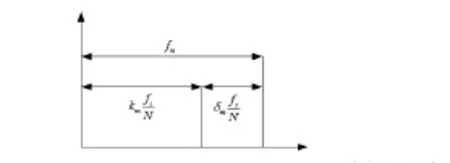
图1　意义的具体描述

式中，k0为采样信号实际的频率分布谱线，fs为采样频率。fm在实际情况中总是会偏移真实谱线的频点，也就是说k0通常不是整数值。所以假设，其中k1是整数，是频移量，δ的具体描述如图1所示。

频移条件判定：首先取k1为被测信号的离散频点对应的一条峰值谱线，假如该峰值谱线邻近的两条峰值谱线k1+1、k1-1的幅值满足：

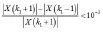
那么就表明第k1+1条谱线峰值和第k1-1条谱线峰值相差很小，进一步说明被测信号的峰值谱线和同步采样时的峰值谱线之间的频域间隔相差很小，不需要频移；相反假如两条峰值谱线k1+1、k1-1的幅值满足：

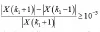
那么就表明第k1+1条谱线峰值和第k1-1条谱线峰值相差较大，进一步表明被测信号的峰值谱线和同步采样时的峰值谱线之间的频域间隔相差较大，需要校正被测信号，通过频移，消除非同步采样造成的误差，实现准同步采样。

频谱搬移的频移量为：

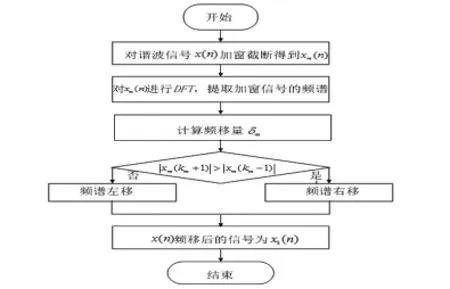
图2　加窗频移算法流程图

2　梳状FIR滤波器的设计

谐波与间谐波之间的相互干扰会进一步降低检测结果的准确性，采用谐波、间谐波分离并分别检测可以有效抑制互扰问题。本设计采用梳状FIR滤波器将采样信号中的谐波信号与间谐波信号进行分离。

由陷波滤波器的归一化（Normalization）响应可知，采样频率必须为陷波带间带宽的整数倍，若不满足此要求，经滤波后的信号会出现频谱泄露现象，影响检测精度。因此，梳状滤波器必须在同步采样前提下使用。

对生成的多项式F（ω）进行归一化（Normalization）处理，可得到梳状FIR滤波器的零相位传递函数Q（ω）：

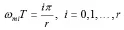
则归一化常量C为：

在滤波器设计过程中，实数阶数n应取距离n值较近的偶数整数值，且此偶数整数值须大于等于n。变大的n值不会引起预设的陷波带数目和陷波带宽度改变，但是会影响通频带的增益。当对n进行近似处理后，通频带增益α［dβ］将会略微变小。滤波器的冲激响应h（m）中包含2nr+1个系数，其中有n+1个为非零量。

由以下公式评价滤波器的实际带通衰减：

设计一个具有10个陷波带数的等纹波梳状滤波器，陷波带宽度为，最大的通带衰减为。综合考虑谐波、间谐波的分离效果和阶数对滤波器的影响，设计滤波器：，其中表示采样点个数。设采样序列经过准同步化后，采样频率变为10kHz，计算出的基波频率为50.2Hz，则r =214。滤波器的仿真结果如图3所示。

图3　梳状FIR滤波器冲激响应和幅频响应

3　Prony谱分析算法

Prony谱分析法用一组指数函数的线性组合来拟合等间距采样数值，其将自回归思想或者自回归滑动思想以及最小二乘法结合起来，来检测被测信号的幅值、频率以及相位。

构造表示拟合误差值的目标函数为：

假设误差平方和ε为最小，那么可以通过解非线性方程组，求取得到参数的值。但是这种方法计算过程非常复杂。Prony算法最为核心的思想就是可以把被测信号采样序列通过式（9）拟合成求解一常数线性差分方程的齐次解。

式中，阶数P是通过自回归模型的奇异值分解来选择的。通过求解式（11）得到zi（i=1,2,…，p），进一步推出：

根据式（12）可得矩阵方程Vb=x：

其中：

式（13）的最小二乘解为：

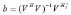
由bi（i=1,2,…，p）可得：

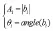
4　仿真结果

我们分别对目前广泛采用的加窗插值FFT算法，基于准同步采样的梳状滤波加窗查值FFT算法，以及基于准同步采样的梳状滤波Prony谱分析法进行对比仿真分析。

（1）加窗插值FFT算法（WI-FFT）［5-7］，使用Hanning窗抑制频谱泄漏，使用谱线插值算法减小栅栏效应，由FFT谐波测量公式计算各次谐波的参数。其程序算法框图如图4所示。

图4　加窗插值FFT算法（WI-FFT）程序框图

（2）基于准同步采样-梳状滤波器-加窗差值FFT算法（QS-WIFFT）［8］，使用频移算法计算频率偏移因子，形成准同步采样序列。用时域平均法将谐波信号与间谐波信号进行分离，并使用加窗查值FFT算法对谐波、间谐波信号分别检测。其程序算法框图如图5所示。

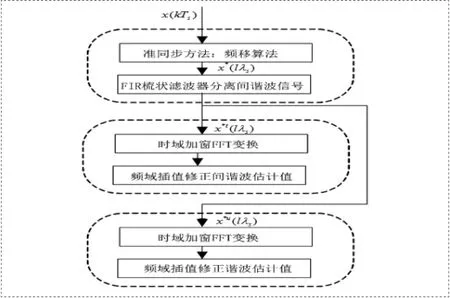
图5　基于准同步采样-梳状滤波器-加窗差值FFT算法（QS-WI-FFT）程序框图

（3）基于准同步-梳状滤波器分离-Prony谱分析算法（QS-Prony），在上述算法（2）中分离的谐波、间谐波准同步序列的基础上，采用Prony谱分析法拟合得到各次谐波的各项参数。其程序算法框图如图6所示。

设定电网谐波、间谐波信号模型为：（17）

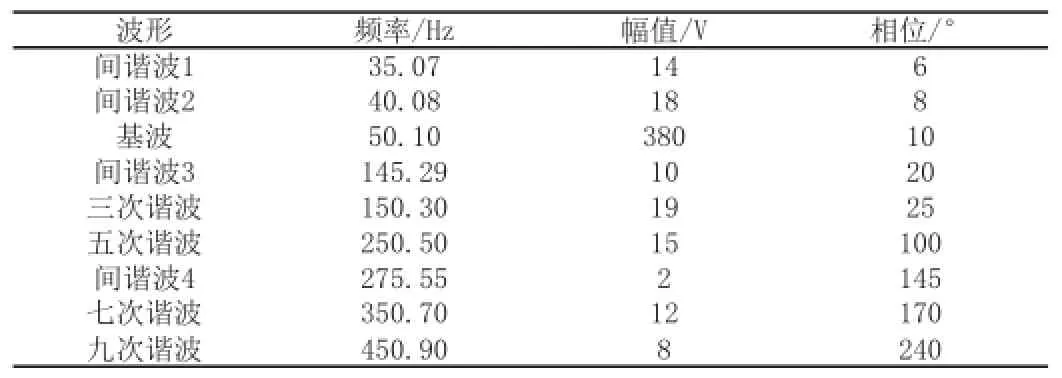
表1　谐波、间谐波参数设定值

被测信号的频率、幅值、相位参数设定值如表1所示，所设定的谐波，间谐波的频率值，其整数倍数不等于采样频率，故本次采样为非同步采样［11］。

表2　WI-FFT、QS-WI-FFT、QS-Prony频率仿真结果

表3　WI-FFT、QS-WI-FFT 、QS-Prony幅值仿真结果

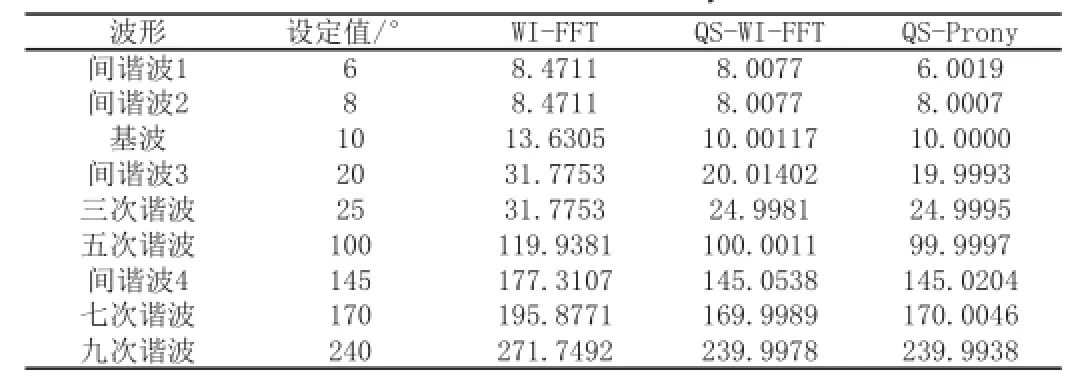
表4　WI-FFT、QS-WI-FFT 、QS-Prony相位仿真结果

WI-FFT算法受非同步采样的影响，无法精确检测频率、幅值、相位信息，QS-WI-FFT和QS-Prony均可较为精确地检测各次谐波、间谐波信号。QS-Prony相较FFT算法可以实现较高的频率分辨率，检测结果符合IEC检测标准，且比传统的FFT改进算法具有更高的谐波、间谐波检测精度。

5　结论

基于频移算法的准同步谐波和间谐波检测实现非同步采样信号的准同步化，提高谐波和间谐波的分离精度。采用梳状滤波的分离方法可以有效分离信号中谐波与间谐波信号，实现两者的分别检测。Prony谱分析法用一组指数函数的线性组合来拟合等间距采样数值，相较FFT算法可以实现较高的频率分辨率，实现了更高的检测精度。

参考文献

［1］Sterken C.Jean Baptiste Joseph Fourier［J］.Nature，2003，292（292）：710.

［2］Qin L，Guo Q，Hao C，et al.Application of hamming windowed interpolated DFT algorithm based on modified ideal sampling frequency in on-line measuring dielectric loss angle［C］.International Conference on Electric Utility Deregulation and Restructuring and Power Technologies.IEEE，2011：1226-1231.

［3］Varaprasad O V S R，Panda R K.A novel synchronous sampling algorithm for power system harmonic analysis［C］.India Conference. IEEE，2013：1-5.

［4］Sun Z M，Huang J，Yang J，et al.A High Accuracy Analysis Method for Harmonics and Inter-harmonics in Power Systems Based on Dolph-Chebyshev Windows［J］.Automation of Electric Power Systems，2015，39（7）：117-123.

［5］Zhao G Q，Gu Y Y.Research on harmonic current detection based on spectral line interpolation FFT［J］.Computer Engineering and Design，2014.

［6］李得民，何怡刚.基于Nuttall窗四谱线插值FFT的电力谐波分析［J］.电力系统保护与控制，2016，V44（3）：64-71.

［7］Lan H，Long F，Wang Y R，et al.Application of Improved Single-Peak Spectral Line Interpolation Algorithm in Harmonic Check［J］.Journal of Northeast Dianli University，2009.

［8］吴超凡，陈隆道.基于分段插值同步化算法的谐波测量［J］.电力系统保护与控制，2016，V44（9）：1-6.

［9］王玲，冯宇，邱进，等.电压互感器谐波特性测量用可控谐波电压源的构建［J］.电力系统保护与控制，2015，V43（16）：106-111.

［10］Huang D M，Gong R X，Jiao F C，et al.Power harmonic analysis based on Rife-Vincent window and triple-spectral-line interpolation［J］. Power System Protection & Control，2014，42（2）：28-34.

［11］Arsov L，Iljazi I，Mircevski S，et al.Measurement of the influence of household power electronics on the power quality［C］.Power Electronics and Motion Control Conference.2012：DS1d.7-1-DS1d.7-7.

作者简介：

张浩（1979—），山东枣庄人，毕业于哈尔滨理工大学，中国矿业大学在职研究生，现从事煤矿供电技术的研究工作。

Harmonic and interharmonic detection algorithm based quasi-synchronous Prony technique

Abstract：For the spectral leakage problem of traditional Fourier transform under non-synchronous sampling，and for the interference problems between the harmonic and inter-harmonic，this paper innovatively puts forward a method called quasi-synchronous-comb filter-Prony spectrum algorithm（QSProny）.In this algorithm，the frequency shift method is used to realize the quasi-synchronization of asynchronous sampling signals.In order to avoid the mutual interference between harmonics and inter-harmonics，this quasi-synchronization sequence is further separated by the FIR notch filter.Then，the linear combination of exponential function is utilized by the Prony spectral analysis method to fit the sample data，and the frequency，amplitude and phase of the signal were extracted by using this process.Through the comparison of windowed interpolation FFT algorithm（WI-FFT），quasisynchronous-comb filter separates-windowed interpolation FFT algorithm（QS-WI-FFT）and quasi-synchronous-comb filter separates-Prony spectrum analysis method under different noise environment，it shows that the QS-Prony method can effectively solve the problem of non-synchronization，avoiding the mutual interference problems between harmonic and inter-harmonic effectively.In addition to this，this algorithm has higher frequency resolution compared with the FFT algorithm.

Key words：Harmonic；Inter-Harmonic；Prony algorithm；Comb filter；Matlab