全变分高阶模型的快速去噪算法

山东科技大学数学与系统科学学院 张 倩



全变分高阶模型的快速去噪算法

山东科技大学数学与系统科学学院 张 倩

【摘要】全变分模型的图像去噪，虽然能保持图像边缘，但导致阶梯效应。为了去除阶梯效应，提出了全变分的高阶模型。本文将采用交替方向乘子法（ADMM），对该高阶模型进行求解，并对ADMM算法进行改造，在具体数值求解的过程中使用快速傅里叶变换法，通过仿真实验证明该模型的有效性和优越性。

【关键词】图像去噪；全变分模型；高阶模型；ADMM；快速傅里叶变换

0　引言

在科学研究、军事技术、工农业生产、医学、气象及天文学等领域，图像去噪技术都得到广泛地关注，图像去噪可以帮助人们更加准确地获得我们所需要的图像特征，使其应用到各个研究领域，帮助解决医学、物理、航天、文学等具体问题。

本文关注的是基于全变分高阶模型的图像去噪研究。1992年Rudin等人提出了图像去噪的全变分（Total Variation，TV）模型［1］，该模型在去除图像中原有噪声的同时，能有效地保留图像的边缘信息，但它有一个显著的缺点就是容易产生阶梯效应，也就是图像的平坦区域产生了虚假边界。后来Lysaker、Lundervold和Tai（LLT）提出了高阶全变分模型［2］，去除了阶梯效应，保持了图像平坦区域的光滑度。最近几年，为解决图像去噪模型中，存在的一些非光滑不可微问题，提出了大量快速高效地数值算法：原始对偶混合梯度法（PDHG）［3］，增广拉格朗日方法（Augmented Lagrandian Method，ALM）［4］，交替极小化算法［5］等等。本文在研究全变分高阶模型去噪问题，采用了交替方向乘子法，以及快速傅里叶变换的优化方法求解模型，来提高图像去噪质量和效率。

1　全变分图像去噪模型

全变分（TV）模型表示为求以下泛函的极小值：

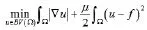
高阶导数全变分模型（HOTV）：

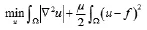
2　本文算法与收敛性分析

最早是在文献［5］提出经典的ADMM算法，在图像处理等领域，这一算法得到了广泛的应用，其求解问题的基本思想是，引入几个辅助变量替换原问题中较难处理的部分，本文结合ADMM算法，在对能量泛函求解时加入快速傅里叶变换，给出一个快速数值求解方法：首先引入两个辅助变量(m，n)。

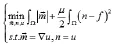
把上述问题转化为无约束优化问题，其增广拉格朗日函数为：

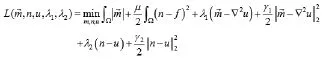
（4）

根据交替迭代的思想，通过固定其他的变量，对某一个变量求最小，下面给出对每一个子问题的具体求解方法：

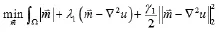
由收缩公式，式（5）等价于：

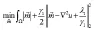
由文献［6］中求解收缩阈算子方法，可得式（6）的解为：

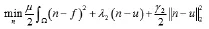
下面关于n进行求导，由于在导数为零处取得极小值。

（3）求解的子问题

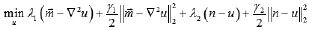
（11）

等价于：

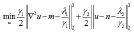
由Euler-Lagrange方程可得：

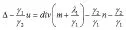
下面求得u，应用快速傅里叶变换及其性质。

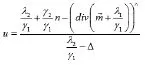
由式（7），（10），（14）得本文算法步骤为：

结合经典的ADMM算法的收敛性分析［7］，由于本文算法添加两个变量，是ADMM算法在图像去噪的一个应用，下面给出文中ADMM算法的收敛性。

3　实验结果与分析

为检验本文ADMM算法在图像去噪的有效性，本节对多幅图像进行仿真实验。下面的图均在Matlab R2013a的环境下进行仿真实验。本文选用常用的“Lena”图像，实验参数选取。算法迭代终止条件为：是用来控制迭代终止的量，本文取

实验对加入噪声的Lena灰度图像进行去噪，分别给出在迭代30次和60次的计算结果。如图1和图2所示。

图1　

图1给出了Lena灰度图像的原图，含噪声图像，以及迭代20次的Chambolle算法和本文算法的去噪图像。

图2　

图2给出了进行数值求解迭代60次时采用Chambolle算法和本文算法的计算结果图像。

通过对比以及视觉观察上面给出的去噪后的图像，可以看出本文算法在进行图像去噪时效果更好，图像更清晰更自然。

由Matlab2013a进行数值实验，当算法终止迭代时，文献［8］的算法在迭代30次和60次的时候，运行时间都要比本文算法多20-30s，所以本文算法与文献［8］算法相比，运行时间大大缩短，从而提高了图像去噪的效率。

4　结束语

本文给出了图像去噪高阶模型，并在求解过程中加入快速傅里叶变换，该算法不仅能够有效地去除噪声，也加快了运算，大大提高了运算时间。通过Lena灰度图进行仿真实验，实验结果表明：对高阶TV模型，加入快速傅里叶变换，进行算法求解是可行的，而且该方法不仅能有效地去除图像中的噪声，还能缩短运行时间。

参考文献

［1］Rudin L I，Osher S，Fatemi E.Nonlinear total variation based noise removal algorithms［J］.Physics D： Nonlinear Phenomena，1992，60（1/4）：259-268.

［2］Lysaker M，Lundervold A，Tai Xuecheng.Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time［J］.IEEE Transactions on Image Processing，2003， 12（12）：1579-1590.

［3］M.Zhu and T.Chan，An Efficient Primal-Dual Hybrid Gradient Algorithm for Total Variation Image Restoration［R］.Ucla Cam report， 2008.

［4］Wu Chunlin，Zhang Juyong，Tai Xuecheng.Augmented Lagrangian method for total variation restoration with non-quadratic fidelity ［J］.Inverse Problems and Imaging， 2011， 5（1）：237-261.

［5］R Glowinski and A Marrocco.Sur l'approximation parelements nisd'ordreun， etlan resolution par penalisation-dualite， d'une classe de problemes de Dirichlet non lineaires［M］. Journal of Equine Veterinary Science， 1975， 31（s 5-6）：41-76.

［6］Yang J，Yin W，Zhang Y，et al.A fast algorithm foredge-preserving variational multichannel image restoration ［J］.SIAM Journal on Imaging Sciences，2009，2（2）： 569-592.

［7］J.Eckstein and D.Bertsekas，On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators［M］.Mathematical Programming，1992，55：293-318.

［8］宋锦萍，郑昌燕.高阶模型的快速图像修补［J］.计算机工程与应用， 2015， 51（11）：154-157.

［9］胡学刚，张龙涛，蒋伟.基于偏微分方程的变分去噪模型［J］.计算机应用，2012， 32（7）： 1879-1881. 1901.

作者简介：

张倩（1991-），女，山东胶南人，山东科技大学硕士研究生。