CPTU确定饱和土体水平渗透系数的改进方法

李镜培，李险峰，张亚国

(1.同济大学 土木工程学院地下建筑与工程系，上海200092；2.岩土与地下工程教育部重点实验室(同济大学)，上海200092)



CPTU确定饱和土体水平渗透系数的改进方法

李镜培1,2，李险峰1,2，张亚国1,2

(1.同济大学 土木工程学院地下建筑与工程系，上海200092；2.岩土与地下工程教育部重点实验室(同济大学)，上海200092)

摘要:目前采用的球面流或半球面流模型所预测的饱和土体渗透系数普遍低于实测值,为提高孔压静力触探(CPTU)测试技术确定饱和土体水平渗透系数的准确性，针对初始超孔隙水压力的分布形式、孔压过滤环的位置和渗流模型3个主要问题，在回顾前人方法基础上，提出一种基于CPTU确定饱和土体水平渗透系数kh的改进方法.根据已有研究成果，将锥肩附近初始超孔隙水压力视为负指数型衰减分布，结合圆柱面径向渗流模型，推导出饱和土体水平渗透系数的计算公式，应用算例验证了本文方法的合理性，再结合上海某地的实测数据，将本文方法与已有方法进行对比分析，研究结果显示：本文方法计算的渗透系数大于已有方法，更接近室内渗透试验的结果；CPTU测试技术可用于连续且快速地计算饱和土体水平渗透系数.

关键词:孔压静力触探；饱和土体；改进方法；水平渗透系数

孔压静力触探(CPTU)测试技术是一种快速、经济、有效的原位测试方法，在国际上广泛应用于岩土工程实践.CPTU测试技术能测出近乎连续的锥尖阻力qt，侧壁摩阻力fs和孔隙水压力ua等参数，可用于土分类、土工特性评价以及工程设计等[1-2].

由于孔压消散试验耗时长的缺点，许多学者致力于用CPTU测试技术确定饱和土体的渗透系数.其中大多数方法是经验性的，比如利用CPTU划分土类的方法确定渗透系数的大致范围[3].而Elsworth等[4-5]的方法(简称Elsworth方法)和Chai等[6]的方法(简称Chai方法)采用位错理论结合球面流或半球面流模型，推导出CPTU测试指标与渗透系数之间的理论关系式.

但是以Elsworth方法和Chai方法为代表的球面流和半球面流模型主要存在以下3个问题：

1)Chai方法推导公式时，假定初始超孔隙水压力呈幂函数分布的形式，但该假定缺乏合理性，初始超孔隙水压力为负指数型衰减分布更为合理[7].

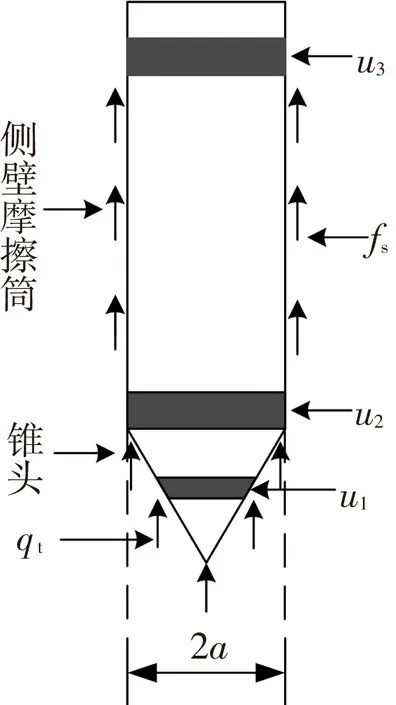
2)Elsworth方法和Chai方法都没有指明实测孔隙水压力的位置，即对孔压过滤环位于锥面(u1)、锥肩(u2)和侧壁摩擦筒后部(u3)时测得的孔压没有做区分[1, 6]，这会影响计算结果的准确性.

3)Elsworth方法和Chai方法计算的渗透系数是水平方向的[6]，但是它们分别采用了球面流和半球面流模型的假定，使得超静孔隙水压力的消散是沿垂直于球面方向，而非沿水平方向[1]，显然不太准确.

针对以上问题，提出了一种假定锥肩附近初始超孔隙水压力符合负指数型衰减分布，结合圆柱面径向渗流模型，计算饱和土体水平渗透系数的改进方法.然后通过文献[6]中算例验算了本文方法的合理性，最后根据上海某地的实测资料，将本文方法与前人方法进行对比分析.

1Elsworth方法和Chai方法

为了基于CPTU测试技术更精确地计算饱和土体渗透系数，Elsworth等[4]提出了一种基于位错理论结合球面流模型计算渗透系数的方法，图1为位错理论基本概念图.

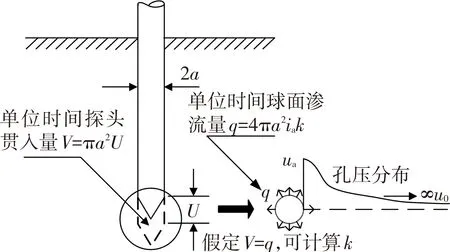
图1　位错理论基本概念图[6]

该方法做出一系列假定[8]：1)在孔压静力触探贯入过程中，动态稳定的孔压水渗流形成的球形孔穴恰好能包裹整个探头；2)探头处形成的球形孔穴的直径等于探头的直径；3)连续性假设：单位时间内孔穴的球形表面渗透流量等于探头贯入量；4)孔压静力触探贯入时在探头附近只形成正的超孔隙水孔压力，在距探头很远处超孔压为零.

再结合达西定律，推导出饱和土体渗透系数k的计算公式：

(1)

其中KD为无量纲渗透系数,

(2)

归一化锥尖阻力Qt和孔压参数比Bq：

(3)

(4)

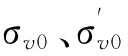
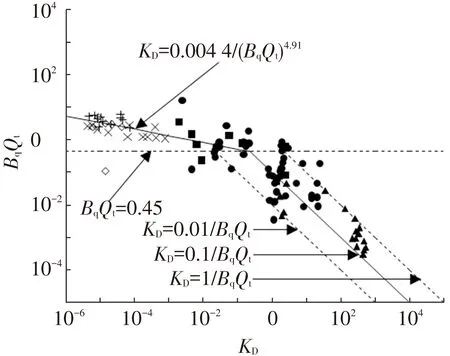
根据实测资料，Elsworth等[5]修正了KD和CPTU测试指标BqQt的关系，见图2，得到如下等式：

(5)

通过CPTU测试指标BqQt可计算KD，再根据式(1)可计算k.

图2　无量纲渗透系数KD和测试指标BqQt的关系

基于Elsworth方法，Chai等[6]提出了半球面流的假定，推导出饱和土体渗透系数k的计算公式：

(6)

对文献[5]中实测数据进行分析，重新修正KD和BqQt的关系，提出了一种双线性模型，即

(7)

2改进方法

Chai方法在计算饱和土体渗透系数时，假定初始超孔隙水压力的分布符合幂函数形式，即

(8)

但研究发现[9]，孔压静力触探过程中，初始超孔隙水压力的分布符合负指数型衰减形式，其表达式为

(9)

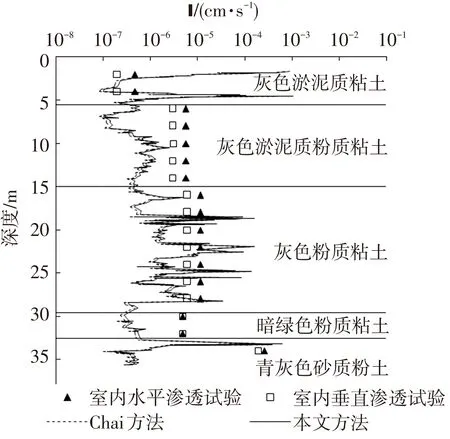
式中：r为空间点与圆柱面的径向距离，a

式(9)中实测孔隙水压力ua的大小与孔压过滤环的位置有关，见图3，孔压过滤环对应不同位置时ua分别为u1、u2、u3.而Elsworth方法和Chai方法并没有具体指明孔压过滤环的位置，会使计算结果不准确.由已有研究成果[1]知，孔压过滤环位于锥肩时，超静孔隙水压力的消散应当沿孔压过滤环的径向方向流出，如图4所示，为沿圆柱面(孔压过滤环表面)的水平向消散，而无法向上流入探头内部，也无法向下流入圆锥头内.所以，考虑到实际工程中孔压过滤环一般位于锥肩处，采用圆柱面径向渗流模型能更准确地计算饱和土体的水平渗透系数.

图3　CPTU孔压过滤环位置

图4　圆柱面流动[1]

根据上述说明，本文基于已有研究做出如下假定：

1)孔压过滤环位于锥肩时，超静孔隙水压力的消散符合圆柱面径向渗流模型.那么，CPTU实测孔隙水压力为

(10)

2)在孔压静力触探贯入过程中，锥肩附近初始超静孔隙水压力的分布为负指数型衰减形式.那么，结合式(9)和(10)可得圆柱面r=a 处的孔压梯度为

(11)

3)连续性假设,单位时间内通过半径为a的圆柱面的渗流量等于探头的体积贯入量，则存在：

2πahkhia=πa2U,

(12)

式中h为孔压过滤环厚度.

结合式(11)和(12)，可推导出饱和土体水平渗透系数为

(13)

对于国际标准规格的CPTU探头，探头直径为2a=35.7mm，孔压过滤环厚度h=5mm，则式(13)可化为

(14)

对比式(1)和(14)可知，本文方法的KD约是Elsworth方法的0.042倍.根据文献[5]中实测数据，将其KD乘以0.042可折减成本文方法对应的KD，如图5所示.观察图5，可得关系式：

(15)

图5　修正后无量纲渗透系数KD和BqQt的双线性关系

由图5可知，式(15)在双对数坐标系中是两段直线，即KD与BqQt之间呈双线性关系.考虑到在工程实践中，渗透系数的误差位于一个数量级范围内是可以接受的[1]，图中KD=0.01/BqQt和KD=1/BqQt分别为KD=0.1/BqQt一个数量级范围内的下限和上限.从图5还可看出，实测数据基本在误差允许范围内.

Elsworth方法和Chai方法只考虑了孔压静力触探贯入过程中产生正的超静孔隙水压力的情况，适用性受到限制.由于本文方法是以Elsworth方法和Chai方法为基础，故而也仅适用于正常固结或轻微超固结的黏性土和松散的无黏性土.

3算例分析

通过文献[6]中算例进行定量计算，将计算结果和已有方法进行对比分析.算例采用国际标准探头，其横截面积为1 000mm2，探头贯入速度U=20mm/s，CPTU测试指标BqQt=3，超孔隙水压力ua-u0=300kPa.将BqQt=3代入式(15)，得到KD约为2.0010-5，再代入式(14)并结合已知条件，可知本文方法计算的饱和土体水平渗透系数约为4.1610-9m/s.由于BqQt为3大于1.2，Elsworth方法不适用，Chai方法计算的结果约为3.5010-9m/s.同时，本文考虑到KD和BqQt之间的双线性关系，继续假定BqQt=0.2，ua-u0=20kPa，其他条件同上，同理可得本文方法计算的结果约为1.0410-4m/s，Elsworth方法计算的结果约为7.1210-5m/s，Chai方法计算的结果约为8.7410-5m/s.

由算例可知，本文方法计算的结果与Elsworth方法和Chai方法基本一致，和实际经验相符合.本文方法计算结果比Elsworth方法和Chai方法计算结果都略大，是Chai方法的1.19倍.从已有资料[1,7]知，Elsworth方法和Chai方法的计算结果普遍低于实测值.所以，本文方法能更准确地计算饱和土体的水平渗透系数.

4工程应用

根据文献[7]中上海某地的实测数据，应用Chai方法及本文方法分别计算了土体的渗透系数，并与室内渗透试验的结果相比较，结果见图6.

本文方法的计算结果与室内渗透试验结果基本在一个数量级范围内，只有小部分灰色淤泥质粉质粘土和青灰色砂质粉土的计算结果与室内渗流试验差异较大.另外，同一土层的渗透系数变化非常明显，推测可能是因为同一土层中含有软弱夹层，导致其渗透系数发生变化.而室内渗透试验由于受到人为确定取样位置等因素的影响，不能反映出这种连续地变化，会导致较大的偏差.

图6　本文方法与Chai方法及室内试验结果的对比

Fig.6Comparisonsbetweenresultsofmodifiedapproach,Chai’smethodandlabtests

5结论

1)本文方法具有合理性，计算的水平渗透系数大于已有方法，是Chai方法的1.19倍，更接近室内渗透试验的结果，进一步提高了计算结果的准确性.

2)CPTU测试技术可以连续且快速地计算饱和土体的水平渗透系数，避免了室内渗透试验不连续和孔压消散试验耗时长的缺点.

3)本文方法适用于正常固结或轻微超固结的黏性土和松散的无黏性土.

参考文献

[1] 邹海峰, 蔡国军, 刘松玉. 基于位错理论的饱和土渗流特性CPTU评价研究[J]. 岩土工程学报, 2014, 36(3): 519-528.DOI: 10.11779/CJGE201403015.

ZOUHaifeng,CAIGuojun,LIUSongyu.EvaluationofcoefficientofpermeabilityofsaturatedsoilsbasedonCPTUdislocationtheory[J].ChineseJournalofGeotechnicalEngineering, 2014, 36(3): 519-528.DOI: 10.11779/CJGE201403015.

[2] 刘松玉, 蔡国军, 邹海峰. 基于CPTU的中国实用土分类方法研究[J]. 岩土工程学报, 2013, 35(10): 1765-1776.

LIUSongyu,CAIGuojun,ZOUHaifeng.PracticalsoilclassificationmethodsinChinabasedonpiezoconepenetrationtests[J].ChineseJournalofGeotechnicalEngineering, 2013,35(10): 1765-1776.

[3]ROBERTSONPK.Estimatingin-situsoilpermeabilityfromCPT&CPTU[C]//Proceedingsofthe2ndInternationalSymposiumonConePenetrationTesting(CPT'10).HuntingtonBeach,California:CaliforniaStatePolytechnicUniversityPomona, 2010: 535-542.

[4]ELSWORTHD,LEEDS.Permeabilitydeterminationfromon-the-flypiezoconesounding[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2005, 131(5): 643-653.DOI: 10.1061/(ASCE)1090-0241(2005)131: 5(643).

[5]ELSWORTHD,LEEDS.Limitsindeterminingpermeabilityfromon-the-flyCPTusounding[J].Géotechnique, 2007, 57(8): 679-686.DOI:10.1680/geot.2007.57.8.679.

[6]CHAIJC,AGUNGPMA,HINOT,etal.Estimatinghydraulicconductivityfrompiezoconesoundings[J].Géotechnique, 2011, 61(8): 1-10.DOI: 10.1680/geot.10.P.009.

[7] 王君鹏, 沈水龙. 基于孔压静力触探确定土体的渗透系数[J]. 岩土力学, 2013(11): 3335-3339.

WANGJunpeng,SHENShuilong.DeterminationofpermeabilitycoefficientofsoilbasedonCPTU[J].RockandSoilMechanics, 2013(11): 3335-3339.

[8]WANGJP,XUYS,MAL,etal.AnapproachtoevaluatehydraulicconductivityofsoilbasedonCPTUtest[J].MarineGeoresourcesandGeotechnology, 2013, 31(3): 242-253.DOI: 10.1080/1064119X.2012.676154.

[9] 朱小林, 唐世栋. 利用孔隙水压力-静力触探探头估算软黏土固结系数的理论分析[J]. 工程勘察, 1986(6): 8-12, 23.

ZHUXiaolin,TANGShidong.Theoreticalanalysisofthecoefficientofconsolidationinsoftclayestimatedbyporewaterpressure-coneofconepenetrationtest[J].GeotechnicalInvestigation&Surveying, 1986 (6): 8-12, 23.

[10]马淑芝, 汤艳春, 孟高头, 等. 孔压静力触探测试机理、方法及工程应用[M]. 武汉: 中国地质大学出版社,2007.

MAShuzhi,TANGYanchun,MENGGaotou,etal.Mechanism,methodsandengineeringapplicationofpiezoconepenetrationtests[M].Wuhan:ChinaUniversityofGeosciencesPress, 2007.

(编辑赵丽莹)

doi：10.11918/j.issn.0367-6234.2016.08.031

收稿日期:2015-10-28

基金项目:国家自然科学基金(41272288)

作者简介:李镜培(1963—)，男，教授，博士生导师

通信作者:李险峰，1431948@tongji.edu.cn

中图分类号:TU413

文献标志码:A

文章编号:0367-6234(2016)08-0185-04

AmodifiedapproachtodeterminehorizontalpermeabilitycoefficientofsaturatedsoilsbasedonCPTU

LIJingpei1, 2,LIXianfeng1, 2,ZHANGYaguo1, 2

(1.DepartmentofGeotechnicalEngineering,TongjiUniversity,Shanghai200092,China; 2.KeyLaboratoryofGeotechnicalandUndergroundEngineering(TongjiUniversity),MinistryofEducation,Shanghai200092,China)

Abstract:To increase accuracy of estimating permeability coefficient of saturated soils using piezocone penetration tests (CPTU), taking account that the permeability coefficient of saturated soils estimated by the existing flow model to the spherical or the hemispherical surface is generally lower than the measured value, a modified approach was proposed, in which the initial excess pore water pressure, the location of filter element and seepage model were studied after the researches on evaluation of permeability coefficient of saturated soils were briefly reviewed. Based on the existing results, the initial excess pore water pressure around the shoulder of the cone was regarded as negative exponential attenuation distribution. Combined with the radial flow model to a cylindrical surface, the expression of horizontal permeability coefficient of saturated soils was derived. The comparison between the predicted and measured values demonstrates that the modified approach is reasonable and effective. The results show that the horizontal permeability coefficient determined by the modified approach is larger than that of previous approaches and more close to the corresponding measured value in laboratory tests. The horizontal permeability coefficient of saturated soils can be continuously and rapidly determined by CPTU.

Keywords:piezocone penetration test; saturated soils; modified approach; horizontal permeability coefficient