抽水蓄能机组分数阶PID控制及参数优化研究

曹 健，李超顺，张 楠，曾 探，陈海兵，朱耀伟

（华中科技大学水电与数字化工程学院，武汉 430074）

抽水蓄能机组分数阶PID控制及参数优化研究

曹 健，李超顺，张 楠，曾 探，陈海兵，朱耀伟

（华中科技大学水电与数字化工程学院，武汉 430074）

由于抽水蓄能机组水泵水轮机调节系统结构复杂，工况类型多且转换频繁，容易受水泵水轮机全特性曲线反“S”特性的影响，因此其运行稳定问题比一般机组更加严峻，严重时甚至会影响到电网的供电质量和安全稳定。本文针对传统PID控制在抽水蓄能机组应用中的不足，提出了抽水蓄能机组的分数阶PID（FOPID）控制及其参数优化方法。为提高FOPID控制参数优化效果，提出了一种模糊引力搜索算法（FGSA），该算法在迭代搜索过程中，对引力衰减指数进行动态的模糊推理，使之随搜索代数的改变不断自适应调整，从而通过控制引力常数的大小实现对算法局部和全局搜索进行动态调整，提高算法优化能力。以我国某抽水蓄能电站机组为研究对象建立其调节系统仿真模型，运用不同优化方法和控制规律的组合控制策略进行控制，对比试验结果表明，本文提出的FGSA-FOPID控制策略能有效改善抽水蓄能机组水泵水轮机调节系统在空载工况下频率扰动时的动态性能。

抽水蓄能机组；分数阶PID；参数优化；模糊引力搜索算法；空载工况

0 引言

随着我国风电、光伏发电等新能源和核电在电网中所占比重逐步提高，抽水蓄能作为一种有效调节电源在电网中的重要性日益凸显。抽水蓄能机组在电网中承担着调峰、填谷、调频、调相、事故备用和蓄洪补枯等任务，在保证电网供电质量和可靠性、提高电力系统安全经济稳定运行发挥着重大作用[1]。水泵水轮机是抽水蓄能机组的主要设备，由于水泵水轮机本身的可逆性设计，在运行时水泵水轮机将不可避免地受到反“S”特性的影响，当机组运行在反“S”特性区域时将出现极其不稳定的现象。抽水蓄能机组与常规水电机组相比，工况种类多、工况转换频繁，加之受到反“S”特性的影响，因此比常规水电机组更加难以控制[2]。

实际应用中，抽水蓄能机组的控制规律一般采用PID控制，通过设计PID控制器并优化控制参数有望提高机组的控制品质。由于传统PID控制规律应对复杂的非线性系统时存在着一定不足，人们尝试对PID控制规律进行改进，深化了非线性PID[3]和分数阶PID（FOPID）[4,5]等新型PID控制规律。FOPID控制是传统整数阶PID控制的发展产物，比传统的整数阶PID控制多了两个可调节的参数，积分阶次和微分阶次，因此FOPID比传统的整数阶PID控制器有更好的动态性能[4]。本文将用FOPID控制器对抽水蓄能机组调节系统进行控制。但由于多了两个可调参数加之分数阶的引入使得设计难度增大，参数整定成为难题。

常规水电机组PID控制参数整定方面的研究较多，为了得到更好的调速器参数，专家提出了很多整定算法，传统的整定方法有正交法和单纯行法，虽然这些算法比较简单，精度不高，难以满足控制要求。近几年来，学者们将启发式随机优化方法应用到水电机组PID控制的参数整定，取得了不错效果。常用的算法有粒子群优化算法[6]、遗传算法[7]、混沌优化[8]，菌群优化[9]，引力搜索算法（GSA）[3]等等。相对于其他方法，GSA是一种基于万有引力的启发式随机优化方法，有着较强的收敛速度的全局搜索能力[10]，因其优异的优化性能，受到学者的关注，在控制参数优化[3,11]、系统辨识[12-13]等领域取得了成功应用。在研究中学者们发现，引力常数函数控制算法的全局和局部搜索能力，合适的引力常数变化规律对提高GSA算法性能显得尤为重要[14]。改进引力常数变化规律成为进一步提高GSA算法优化能力的重要方向。

为提高抽水蓄能机组的控制效果，本文尝试将FOPID引入到抽水蓄能机组控制，进一步提出一种模糊引力搜索算法，解决FOPID的参数优化整定问题。为验证本文所提方法的有效性，建立了我国某抽水蓄能电站机组的仿真平台，设计了空载频率扰动试验，对比了分别采用PID和FOPID控制并运用不同优化方法进行控制参数优化的控制效果，试验结果验证了本文方法的有效性。

1 抽水蓄能机组水泵水轮机调节系统模型

抽水蓄能机组水泵水轮机调节系统是由引水系统、水泵水轮机、发电机、调速器和接力器等单元所组成的复杂非线性系统[15]。本文重点阐述引水系统模型、水泵水轮机模型和控制器模型，其它部分如接力器采用两阶模型，发电机采用一阶模型。系统整体模型如图1所示。

1.1 引水系统模型

引水系统模型由水击方程描述。本文采用二阶弹性水击模型描述压力引水系统特性。其传递函数为：

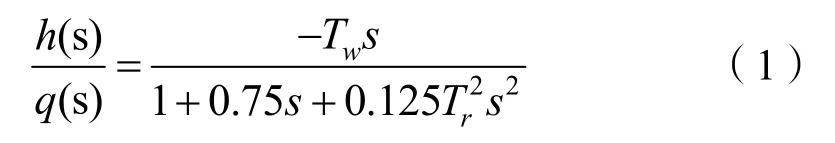
其中，Tw为引水系统水流惯性时间常数；Tr为水锤压力波反射时间，即水锤相长。

1.2 水泵水轮机模型

水泵水轮机模型可用力矩和流量方程表示：.

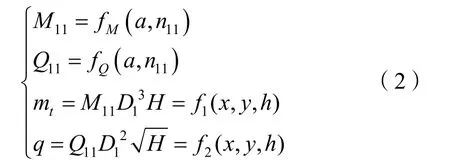
其中，M11为单位力矩；Q11为单位流量；a为导叶开度；n11是水轮机的单位转速，mt=(Mt-Mt0)/Mtr为力矩偏差相对值；q=(Q-Q0)/Qr为流量偏差相对值；D1为转轮直径；H为工作水头；x=(n-n0)/nr转速偏差相对值；h=(H-H0)/Hr为水头偏差相对值；y=(a-a0)/amax为接力器行程偏差相对值，下标“0”表示初始值，下标“r”表示额定值。M11和Q11可以用水泵水轮机力矩特性曲线和流量特性曲线描述，在式（2）中用非线性函数fM和fQ表示。由于其水泵水轮机特性曲线呈现反“S”特性，在反“S”特性区域内，曲线两端还会出现严重的交叉、聚集和扭卷现象，一组转速和导叶开度可能会对应多个单位流量值，导致无法通过插值计算M11和Q11。所以为了克服水泵水轮机的反“S”特性，学者们提出了一些数值变换的方法[16]，本文采用对数投影法。对于流量和力矩特性曲线，纵坐标不变，只是对其中的单位转速n11做对数投影。

变换方法如下：

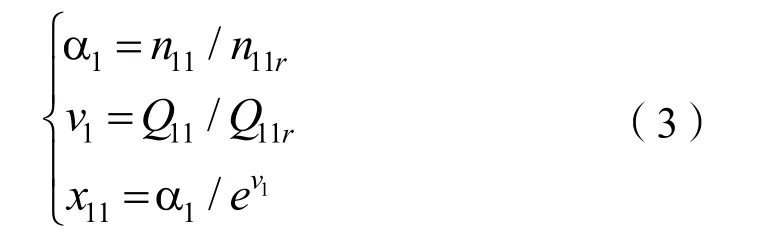
将单位转速投影成x11后，可解决插值计算多值问题。

1.3 分数阶PID控制器模型

分数阶PID控制器是传统整数阶PID控制器的广义化形式，其传递函数为：

其中，e为控制偏差；u为控制器输出；Kp、Ki和Kd为增益参数；为积分阶次；为微分阶次。

图1 抽水蓄能机组水泵水轮机调节系统框图

2 模糊引力搜索算法（FGSA）

2.1 引力搜索算法（GSA）

现在，考虑一个D维搜索空间中有N个粒子，定义第i个粒子的位置为：

其中，t为迭代次数；fi(t)表示粒子i的适应值，即目标函数值。对于极小化问题，

粒子i受到来自粒子j的引力为：

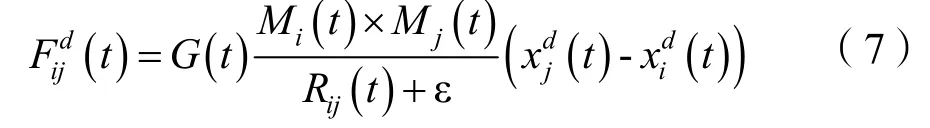
其中，粒子i和粒子j之间的距离可用欧拉距离表示，是一个很小的常量；表示引力常数。

G0为引力常数初值；为衰减指数；T为最大迭代次数。为了增加算法的随机特性，定义第i个粒子所受合力为其他粒子对其引力的随机加权和：

其中，randj是[0,1]之间的随机数。根据牛顿第二定律，物体的加速度与物体所受的力成正比，与物体的惯性质量成反比：

其中，Mi是粒子i的惯性质量。粒子的位置和速度更新为：

其中，randi是[0,1]之间的随机数。

2.2 引力衰减指数的模糊推理

从GSA理论可知，引力常数G在粒子加速度的计算中起着至关重要的作用，而引力衰减指数又影响G的变化速度。当值较大时，G以很快的速度下降，算法的收敛速度加快，反之当值较小时，常量以较慢速度下降，算法的收敛速度变缓。因此是引力搜索算法的关键因子，而普通GSA算法中为常数，无疑限制了算法性能的发挥。为了平衡算法的全局和局部搜索能力，在算法前期值要较小，防止算法陷入局部最优值；在算法后期，值要较大，加快算法的收敛速度，提高最优解精度。

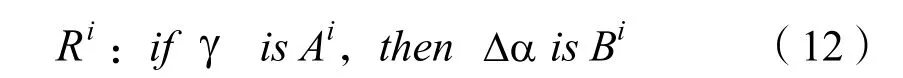
其中，i=1,…,m, 本文取m=4。模糊子集集合A={L, ML, MH, H}，输入变量的隶属度函数采用三角函数，对应的三角函数参数为L:[0,0.2]，ML:[0,0.4,0.8]，MH:[0.2,0.6,1]，H:[0.8,1]。输入变量隶属度函数如图2所示。

图2 输入变量隶属度函数

本文中模糊控制采用中心平均解模糊法，令模糊推理输出向量为即：

以T=50，为例，经模糊推理后引力常数衰减指数变化过程和对应的引力常G数变化过程如图3和图4所示。图3和图4显示，采用模糊推理后，变化规律有明显的变化，更符合不同搜索阶段要求。

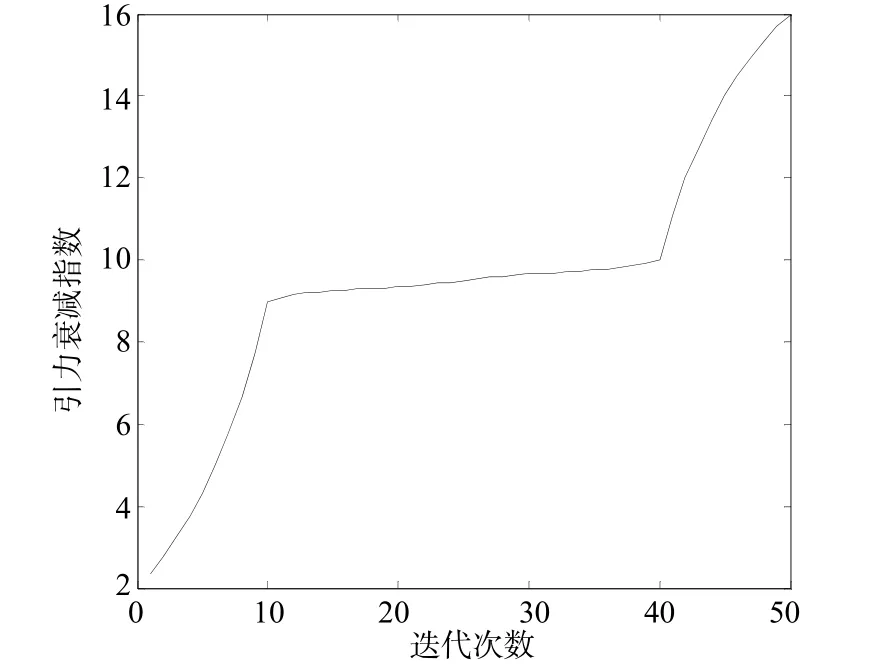
图3 迭代次数T与的关系

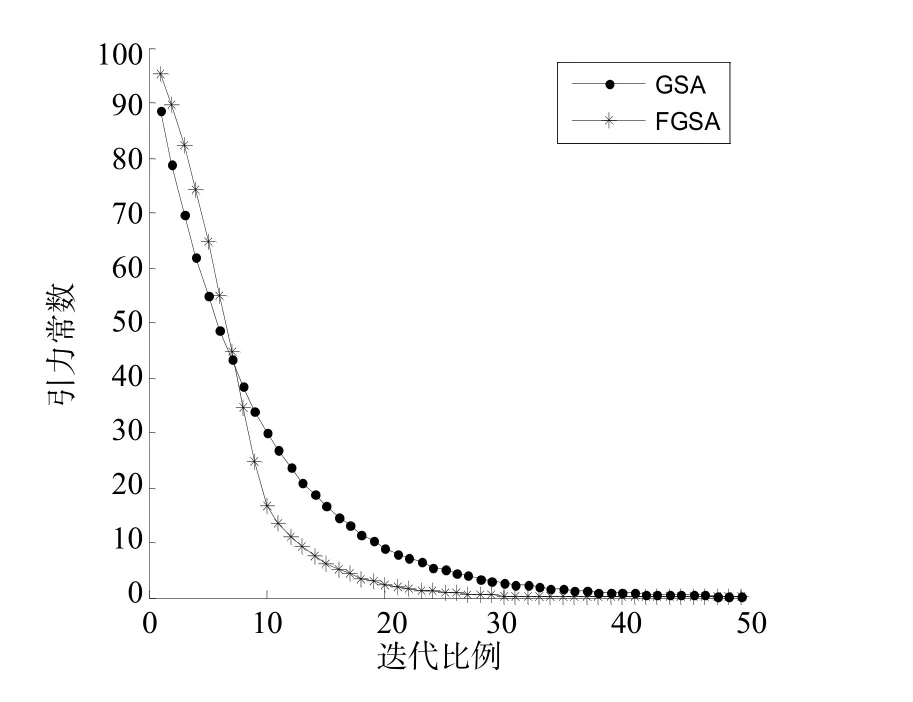
图4 迭代比例与G的关系

2.3 FGSA算法流程

本文提出的FGSA算法在GSA算法基础上，运用模糊推理自适应调整引力常数衰减指数，通过修正引力常数变化规律，在搜索前期引力相对较大，使得粒子具有较大加速度，搜索范围更广，有利于跳出局部极值点；在搜索后期，引力常数相对较小，使得粒子加速度相对变小，进入细搜索阶段，有利于得到最优解。综上所述，算法流程如图5所示。

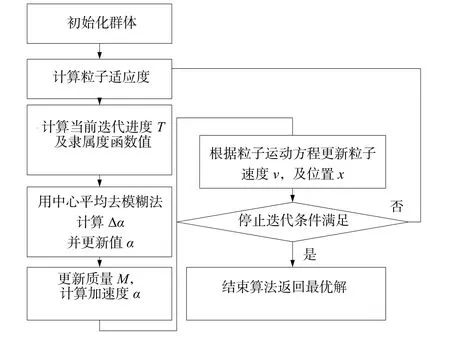
图5 基于模糊控制的万有引力搜索算法流程

3 基于FGSA的FOPID参数优化

3.1 目标函数

采用常用的离散形式ITAE指标最为控制参数优化的目标函数，其定义为：

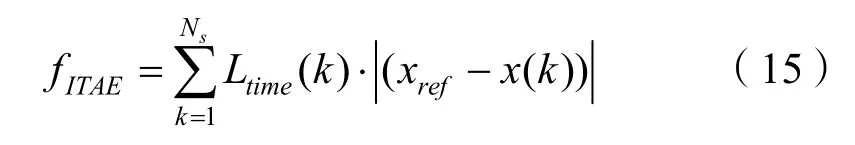
其中，xref为参考频率值；x为频率响应曲线；Ns为采样点数；Ltime为时间序列。ITAE指标越小，对应的动态响应效果越好。

3.2 参数优化流程

运用FGSA优化PID控制参数，其优化变量为控制参数。以FOPID控制参数优化为例，优化变量用向量表达为在优化过程中，优化变量映射为FGSA中的粒子位置向量，向量维数D=5。FGSA优化FOPID控制参数具体步骤如下：

Step 1：算法初始化。设置算法参数，包括群体规模N、最大迭代次数T、引力常数初值G0、衰减指数初始值0；确定优化控制参数范围在此区间初始化群体位置初始化历史最优适应度值fopt和最优解Xopt，设置迭代次数t=0；

Step2：计算当前迭代比例及隶属度函数值；

Step3：按照式(13)和式(14)更新值；

Step4：按照式(15)计算粒子适应度

Step5：求出群体最优目标函数值和对应的粒子位置如果则

Step 6：依据式(6)计算粒子质量依据式(7)-(9)计算粒子引力依据式(10)计算加速度

Step 7：依据式(11)更新粒子速度和位置；

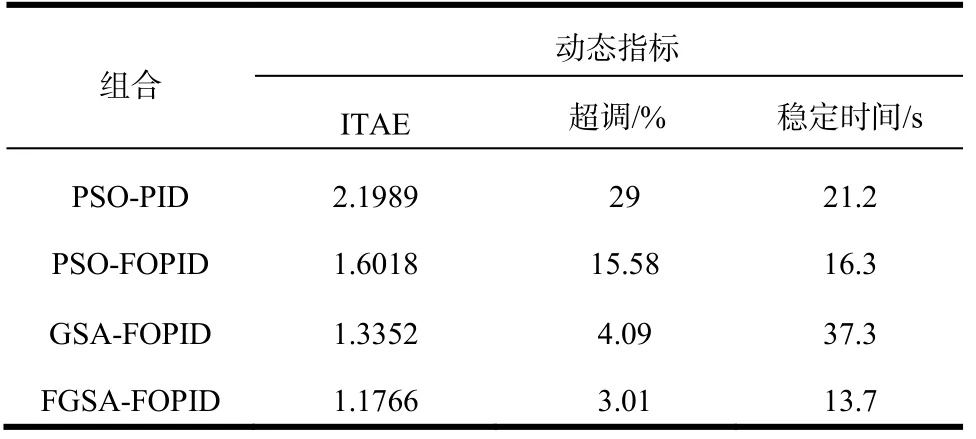
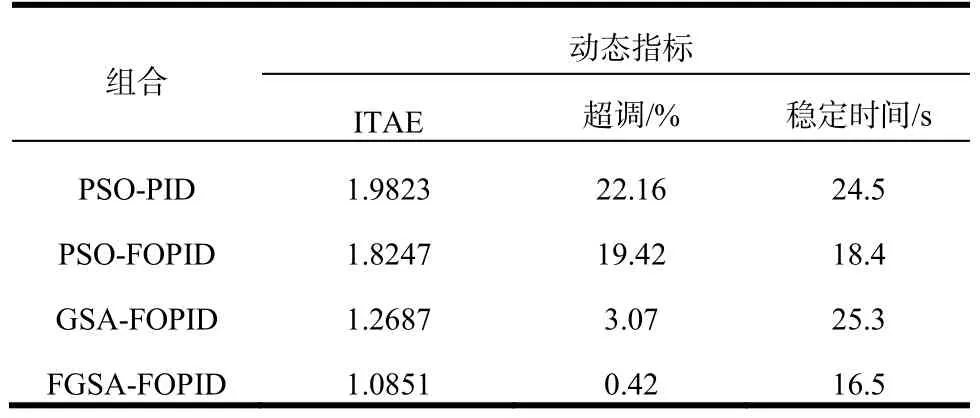
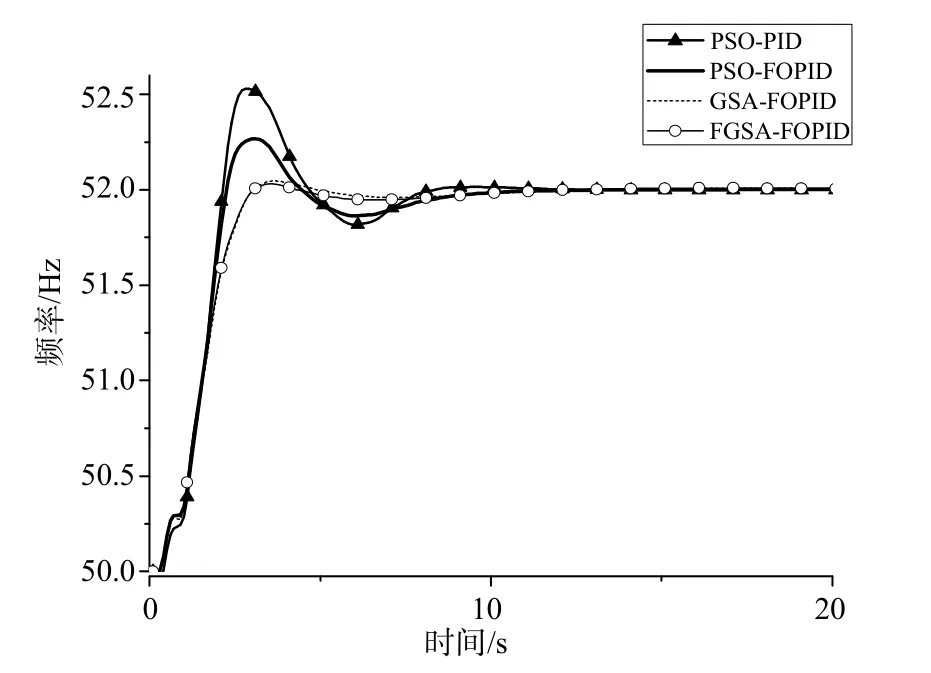
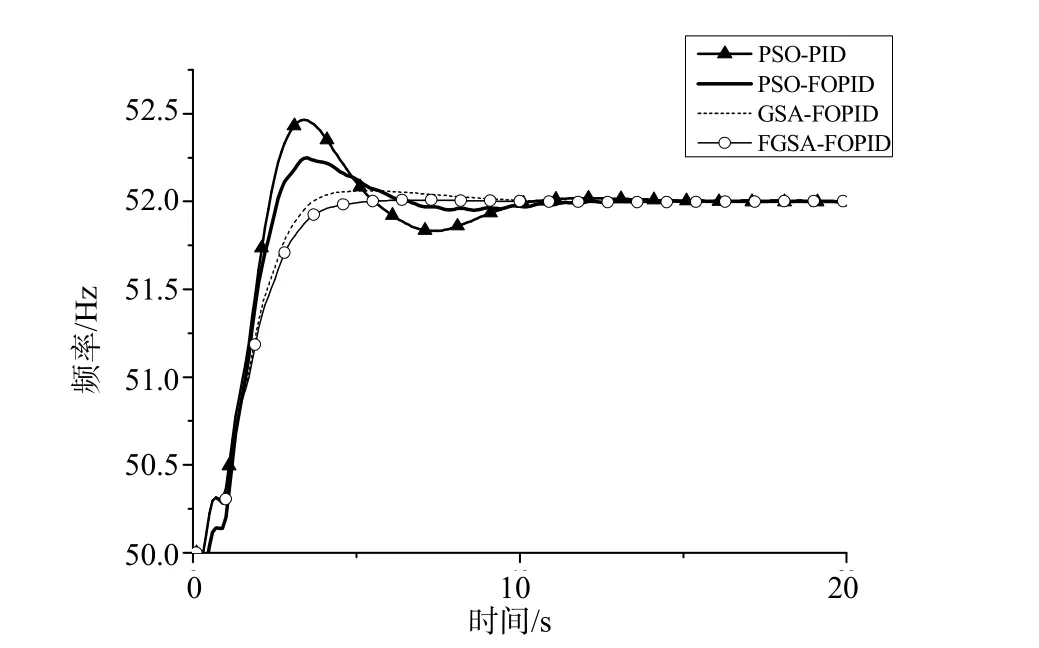
Step 8：t=t+1；如果t

4 实例研究

本文以某抽水蓄能电站机组调节系统为研究对象，按照前文建模方法建立水泵水轮机调节系统仿真模型，进行不同水头下空载开度频率扰动试验。该仿真模型控制器可设置为PID控制或FOPID控制。该抽水蓄能电站的最大水头217m，额定水头195m。本文选择205m和210m两种水头进行空载频率扰动仿真试验，频率扰动值为+2Hz。分别采用不同的优化算法对PID和FOPID控制器参数进行优化，并比较PSO-PID、PSO-FOPID、GSA-FOPID、FGSA-FOPID四种组合策略的控制效果。

PSO参数设置为：群体规模N=20，最大迭代次数T=100，控制参数c1=2，c2=2，动态权重从1到0线性递减；GSA参数设置为：N=20，T=100，G0=20，α=6；FGSA参数设置为：N=20，T=100，G0=20，α0=6。不同组合策略的和控制指标结果对比见表2～表3；机组频率的动态响应曲线对比如图6～图7所示；适应度函数值的迭代过程曲线如图8～图9所示。

表2 FOPID与PID不同算法空载频率扰动控制参数和品质对比（水头205m）

表3 FOPID与PID不同算法空载频率扰动控制参数和品质对比（水头210m）

图6 空载工况+2Hz频率扰动下的频率动态响应（水头205m）

图7 空载工况+2Hz频率扰动下的频率动态响应（水头210m）

图8 空载工况+2Hz频率扰动下的适应度收敛曲线(水头205m)

图9 空载工况+2Hz频率扰动下的适应度收敛曲线(水头210m)

从试验结果可以看出，对比不同水头下的结果可以发现，各控制策略在205m水头试验得到的控制指标普遍劣于210m水头指标，说明抽水蓄能机组低水头更难稳定，这与水泵水轮机的反“S”特性有关。对比PSO-PID和PSO-FOPID结果，可以发现两种水头试验中，FOPID控制效果均优于PID控制，稳定时间和超调量等控制指标提升明显，说明FOPID在抽水蓄能机组控制中具有更好的应用前景。

对比GSA-FOPID和FGSA-FOPID结果，可以发现FGSA优化效果优于GSA，验证了FGSA在控制参数优化中的优异性能。对比PSO、GSA和FGSA的迭代收敛过程，可以发现FGSA寻优能力和收敛性能更佳。

5 结论

针对抽水蓄能机组的控制问题，利用FOPID控制对于非线性控制对象具有适用性的特点，本文在抽水蓄能机组控制中引入了FOPID控制，并提出了一种模糊引力搜索算法对控制参数进行优化。通过仿真试验结果的对比分析，初步得到如下结论：

（1）仿真试验表明FOPID比PID更适合抽水蓄能机组控制，能有效提升机组低水头控制品质；

（2）通过模糊推理自适应调整引力常数衰减系数，有效提高了FGSA的优化能力，在控制参数优化中取得了较好效果；

（3）本文提出的FGSA-FOPID组合控制策略能有效提升抽水蓄能机组的控制品质，具有较好的工程应用前景。

[1] 曹明良．抽水蓄能电站在我国电力工业发展中的重要作用[J]．水电能源科学，2009，27(2)：212-214．

[2] Cai X, Tong D, Zhang L. A new governor control algorithm to suppress the pumped-storage unit" S" shape characteristic influence [C]. 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 2012.

[3] 周建中, 赵峰, 李超顺. 基于GSA的水轮机调速系统非线性PID控制参数优化方法研究[J]. 水电能源科学, 2014,32(12): 127-130.

[4] 薛定宇, 赵春娜. 分数阶系统的分数阶PID控制器设计[J]．控制理论与应用. 2007, 24(5): 771-776．[5] 姚舜才, 潘宏侠. 粒子群优化同步电机分数阶鲁棒励磁控制器[J]. 中国电机工程学报,2010, 30 (21): 91-97.

[6] Fang H, Chen L, Shen Z. Application of an improved PSO algorithm to optimal tuning of PID gains for water turbine governor. Energy Convers Manage 2011, 52(4):1763-70.

[7]康玲. 基于遗传算法的水轮机调速器参数优化方法[J]．水电能源科学, 1999, 17(1):32-34．

[8] Jiang C, Ma Y, Wang C. PID controller parameters optimization of hydroturbine governing systems using deterministic chaotic mutation evolutionary programming (DCMEP)[J]. Energy Conversion and Management, 2006, 47(9): 1222-1230.

[9] 寇攀高, 周建中, 何耀耀, 等．基于菌群-粒子群算法的水轮发电机组PID调速器参数优化[J]. 中国电机工程学报. 2009, 29 (26): 101-106．

[10] Rashedi Esmat, Nezamabadi-pour Hossein, Saryazdi Saeid. GSA: a gravitational search algorithm [J]. Information Science, 2009,179(13): 2232-2248．

[11] 李超顺, 周建中, 肖剑. 基于改进引力搜索算法的励磁控制PID参数优化. 华中科技大学学报（自然科学版）, 2012, 40(10): 119-122．

[12] Li C, Zhou J. Parameters identification of hydraulic turbine governing system using improved gravitational search algorithm [J]. Energy Conversion and Management, 2011, 52(1): 374-381．

[13] Chen Z, Yuan X, Tian H, Ji B. Improved gravitational search algorithm for parameter identification of water turbine regulation system. Energy Conversion and Management, 2014, 78: 306-315.

[14] Li C, Li H, Kou P. Piecewise function based gravitational search algorithm and its application on parameter identification of AVR system. Neurocomputing, 2014, 124: 139-148.

[15] 康玲, 叶鲁卿, 李朝晖. 基于MATLAB的抽水蓄能机组控制系统的仿真研究[J]. 大电机技术, 1999, (1): 55-59.

[16] 林宵汉, 陈乃祥, 李辉, 等．水泵水轮机转轮特性描述新方法及其工程应用[J]. 清华大学学报（自然科学版）, 1999, 39(4)：73-75．

Study on Fractional Order PID Control and Parameter Optimization of Pumped Storage Unit

CAO Jian, LI Chaoshun, ZHANG Nan, ZENG Tan, CHEN Haibing, ZHU Yaowei
(School of Hydropower and Information Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

Because of the complex structure, complicated operation modes and frequently switching of operating conditions, the pumped storage unit (PSU) is easily tends to fall into the “S”feature area. Compared to conventional hydroelectric generating unit, it faces more stability problemsand risk of deteriorating the power supply quality and stability of the entire grid. Respect to the disadvantages of PID control on PSU, this paper proposed fractional PID (FOPID) control and corresponding parameter optimization method. In order to improve the effectiveness of parameter optimization of FOPID control, a fuzzy gravitational search algorithm (FGSA) is proposed. In the searching process, the FGSA tunes the gravitational attenuation index adaptively by fuzzy inference. By controlling the value of the gravitational constant, the exploration and exploitation of the algorithm can be adjusted dynamically as to improve the ability of the algorithm to optimize parameters. An actual pumped storage power station unit is taken into consideration in our country. Based on comparisons of the control strategies combined of different optimization methods and PID control rules, it’s found that the proposed FGSA-FOPID control strategy can effectively improve the dynamic performance of pumped storage unit regulating system under unload condition with speed disturbance.

pumped storage unit; fractional PID; parameter optimization; fuzzy gravitational search algorithm; unload condition

TK730.4+1

A

1000-3983(2016)02-0050-07

2015-04-01

曹健(1994-)，华中科技大学在校本科，主要从事水电机组建模、仿真与控制方面的研究工作。

审稿人：朴秀日

国家自然科学基金（51479076），中央高校基本科研业务费（2015QN214）