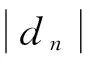基于分形理论的隧道地表沉降分析及预测

左昌群,刘代国,丁少林,李林森

(中国地质大学(武汉) 工程学院， 武汉　430074)



基于分形理论的隧道地表沉降分析及预测

左昌群,刘代国,丁少林,李林森

(中国地质大学(武汉) 工程学院， 武汉430074)

摘要：隧道地表沉降变形时间序列是具有分形特征的非线性体系，以狮子山隧道地表沉降监测为研究对象，基于分形理论，使用R/S分析法和V/S分析法计算了累计沉降和沉降速率时间序列的Hurst指数，并评价了地表沉降的稳定性，结合V统计量评价了这2种分析方法的有效性和地表变形的非循环周期；最后，使用分形插值函数与回归函数对地表沉降值进行了预测评价。结果表明，R/S分析法和V/S分析法对分析地表沉降时间序列具有较好的有效性，R/S分析法受短期记忆影响大，计算结果偏于安全，而 V/S分析法评价地表变形稳定性更加保守，3个监测点将长期处于稳定状态，且其时间序列的非循环周期约为20 d。使用分形插值得到的预测值与实测值间误差较小，且能正确反映变形演化趋势，较传统的回归分析优越，可以为地表沉降预测提供一种参考。

关键词：地表沉降；变形时间序列；分形理论；Hurst指数；分形插值

1研究背景

隧道进出口段常属于围岩风化破碎的浅埋地段，进出口围岩变形的控制是隧道开挖的关键技术之一，对隧道进出口段地表沉降监测及稳定性评价尤为重要，然而由于隧道所处地质环境及变形诱发因素的复杂性，导致地面沉降时程曲线呈现上下波动状态，具有很强的非线性特征。目前对于变形监测分析方法有很多种，靳晓光等[1]考虑到不可预测模糊因素采用灰色模型预测隧道变形，乔志超等[2]采用回归分析模型对隧道围岩变形进行了分析等。然而灰色模型是在光滑离散函数的基础上建立的，在数据较多的情况下会产生较大偏差，回归分析中恰当的回归模型较难确定，造成评价标准具有片面性。

实测隧道地表沉降数据具有突变性、不连续性、时间相关性等特点，分形分析法为隧道地表沉降分析预测提供一种有效途径。基于分形理论的R/S和V/S时间序列分析法[3-4]，对于分析长程相关性的非线性时间序列非常有效。分形理论由法国数学家Mandelbrot等[5]创立，是用来描述一类混乱、复杂而又具有某种规律的自相似性体系。Mandelbrot认为符合于布朗运动的序列即分形时间序列，以长期记忆性为显著特征，具有自相似性。近年来，分形理论已得到广泛应用，Davidson等[6]对分数布朗运动参数的无偏性进行了比较和实证，进一步发展了R/S分析理论。李远耀等[7]、贺可强等[8]运用分形理论R/S分析法，确定位移时序分形Hurst 指数，评价边坡的稳定性。陈学习等[9]、乔美英等[10]分别采用R/S和V/S分析法描述了瓦斯涌出量时间序列的非线性行为。

本文结合分形分析方法与非线性变形参数Hurst指数，并运用分形插值法对隧道地表沉降变形规律进行预测评价，并与传统回归分析法进行对比，对不同分析法的适用性进行了评价。

2基本理论

2.1R/S和V/S分析方法

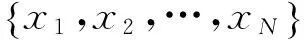
(1)

样本方差为

(2)

由Hurst定义，R/S统计量与V统计量为：

(3)

(4)

Giraitis等[4]采用重标方差V/S代替重标极差R/S，定义的V/S统计量与V统计量为：

(5)

(6)

采用R/S和V/S分析法估计样本时间序列的Hurst指数从而检验其分形特征，并用V统计量验证分形分析法自身的稳定性和时间序列的非循环周期，对于lg(n)，将V统计量逐一标绘于坐标图中，得到V统计量图，曲线图上V统计量由上升趋势转为下降或者转为趋于平稳的转折点对应着的n便是时间序列的非循环性周期天数。

2.2Hurst指数

时间序列的R/S值、V/S值与Hurst指数H存在如下关系：

(7)

(8)

式中K,K′分别为R/S和V/S统计量相关的拟合参数。

由上述原理将时间序列分为无重叠的m组子序列，计算每一组的R/S统计量值和V/S统计量值，再计算其平均值得到不同时间间隔n的平均(R/S)n值和(V/S)n值，以lg(n)为自变量，lg(R/S)n和lg(V/S)n为因变量作对数坐标散点图，然后采用最小二乘法拟合直线，依据直线斜率得到相应的Hurst指数H。

Hurst指数[11-12]取值范围是(0,1)，当H=0.5时，时间序列是独立、随机时间序列；当0.5

2.3分形插值

分形插值函数通过迭代函数系统(IFS)[13]来实现，要想找一个IFS，就必须在给定的集合中找到一组仿射变换，使得仿射变换后的集合通过拼贴能与原集合在Hausdorff距离下尽可能地接近。对于数集{(xi,yi)|i=0,1,…,N}，有N个仿射变换，第N个仿射变换的分形插值函数为

(9)

(10)

当选定了dn而且给定了插值点的集合，便能利用上式求得IFS的各个参数，接着再利用分形迭代算法求取吸引子，该吸引子则是所求的函数图像。

3地表沉降分形分析

3.1工程概况及沉降监测

狮子山隧道为一座分离式隧道。左幅隧道起讫里程桩号为ZK1+830至ZK3+035，长1 205 m，最大埋深120 m；右幅隧道起讫里程桩号为YK1+824至YK3+024，长1 200 m，最大埋深129 m。隧道进出洞口均有岩溶洼地发育。隧道区岩层产状为170°∠3°，隧址区表层下覆盖第四系残坡积粉质黏土(Q4dl+el)，下伏基岩为三叠系下统嘉陵江组(T1j)中厚层状灰岩。

在洞口浅埋段按5 m间距布置监测横断面，对特殊地段可适当增加观测断面，沿衬砌中线，每2～3 m一个测点。选取左洞出口段一监测断面上JC1,JC2,JC3作为研究对象，其观测布置如图1所示，对监测点进行连续50 d监测，结果如图2、图3。

图1　隧道地表沉降测点布置

图2　累计沉降曲线

图3　沉降速率曲线

3.2时序分形评价

对监测点JC1,JC2,JC3时程曲线图进行分段处理，选取时间间隔n的初始值为2，依次增加至25。采集不同时间间隔的累计沉降s与沉降速率v时程序列的(R/S)n和(V/S)n值，绘制对应的双对数曲线图并得到时程序列的Hurst值。本文给出了点JC1的双对数曲线图(图4)。各监测点的计算结果见表1。

图4　JC1累计沉降值与沉降速率R/S和V/S分析

由分析结果可知，采用最小二乘法进行直线拟合，各时间序列双对数图具有较好的线性关系，相关度R最小为0.818，隧道地表变形具有很好的分形特性。由R/S分析法计算各监测点时程序列Hurst指数均大于V/S分析方法得到的结果，使用R/S分析法受序列短期记忆的影响程度更大而高估Hurst指数。累计沉降值的Hurst指数满足0.5

表1　分形分析结果Table 1　Result of fractal analysis

由R/S分析方法计算沉降速率时程序列Hurst指数位于区间[0.516 1,0.592]之中，相对累计沉降值的Hurst指数要小得多，表明沉降速率时程序列受时间记忆影响的敏感度较低，具有较高的随机性，表现出时间序列曲线上下波动幅度大。而由V/S分析方法得到的Hurst指数均<0.5，表明未来的变化趋势与过去相反，具有反持久性，现在处于正增长状态，下个阶段将处于负增长阶段，从而，沉降速率序列曲线还将处于波动阶段。综合对比累计沉降值与沉降速率的Hurst指数，根据Hurst指数偏离0.5的程度大小，得到累计沉降值具有很强的规律性，而沉降速率存在较高的随机性。

3.3V统计量与非循环周期

长期记忆性是分形结构的一个重要特征，而非线性系统中这种长期记忆性也是有界限的，超出了某一界限时间序列对初始值的依赖性降低，系统将表现出相互独立特性。采用V统计量来推断分形分析方法的稳定性和时间序列的非循环周期结果如图5和图6。

图5　累计沉降V统计量

图6　沉降速率V统计量

由图5可以看出，2种方法的V统计量曲线总体上呈现向上倾斜的趋势，符合Peters关于Hurst指数在0.5

如图6所示，由R/S分析法得到的Hurst指数接近0.5，其V统计量曲线向上增长的趋势不明显，趋于水平方向上下波动，找不到明显的拐点，说明沉降速率非循环周期将更长。由V/S分析法得到的Hurst指数<0.5，其V统计量曲线向下倾斜，在lgn=1.3附近，3个监测点曲线图出现转折，初步判断其非循环周期为20 d。

4沉降值预测

4.1分形插值

分形插值根据分形几何的自相似性原理和迭代函数系统理论，将数据插值成具有自相似性结构的曲线。传统的插值拟合方法在相邻的2节点之间通过光滑的曲线相连接，然而测得的地面沉降数据存在一定的波动性，采用传统的插值拟合方法将忽略相邻两点之间的变化特征，根据分形插值原理，可以将插值数据点的变化特征映射到微小的局部区域，得到的数据和原始数据具有自相似性的插值特征，从而更能反映真实变化情况。

仿射变换中的4个参数都由纵向尺度因子决定，因此纵向尺度因子对插值函数的性质起着决定性的影响，经过数据统计发现，纵向尺度因子越大，插值函数波动越大，为了使得插值拟合函数更加逼近原始函数，本文取纵向尺度因子dn=0.04，选取曲线上的拐点或极值点作为插值点，共取插值点19个，进行一次迭代，共生成插值点数325个，图7给出了中点JC2的分形插值结果。

图7　JC2累计沉降值对比

迭代次数与生成的插值点数之间的关系为

(11)

式中：m为生成的插值点数；n为插值点数；k为迭代次数。采用均方根误差对插值结果进行了评价，其公式为

(12)

式中：X为实测值；Xi为预测值；n为样本点数。

根据评价标准得到监测点JC1，JC2，JC3实测值与预测值之间的误差分别为3.825 8%，3.621 1%，4.102 1%。经过分形插值得到的曲线图与原数据图拟合程度高，并且反映了时程曲线的自相似性，表明用分形插值法来预测地面沉降是可行的。

4.2回归分析

为对比分形结果的有效性，采用回归分析法对JC2点沉降值进行预测分析，结果如图8和表2。

图8　JC2累计沉降值回归曲线

回归函数回归方程相关度误差/%一次函数y=-0.115x-2.50.91177.478二次函数y=0.0032x2-0.2806x-1.0650.97034.404指数函数y=-2.7058e0.0248x0.86209.650

通过一次、二次和指数函数分别对JC2沉降值进行回归分析，得到以二次函数的结果最为接近实际值，并与沉降演化趋势一致，而无常数的指数函数背离原值较明显。另外，与分形插值得到的结果相比，回归函数得到的误差偏大。在采用回归分析对变形进行预测时，需要选择合适的回归函数，而对于监测数据较多且变形不规律时，难找出合适的回归函数。

5结论

(1) 隧道累计沉降时间序列是一个复杂的非线性体系，具有记忆性和自相似性，通过R/S分析法和V/S分析法证明了其具有良好的分形特征。

(2) 使用R/S分析法得到的累计沉降和变形速率时间序列的Hurst指数均大于V/S分析法得到的Hurst指数，表明R/S分析法受短期记忆性影响程度大，使用V/S分析法得到的参数更加保守。通过这2种方法预测地表沉降的稳定性得到，3个监测点都将处于稳定状态，且JC3稳定性更高，使用V统计量初步判断累计沉降时间序列的非循环周期为20 d，而沉降速率时间序列的非循环周期可能更久。沉降速率的Hurst指数接近0.5，甚至<0.5，其随机性较大。

(3) 分形插值法可以反映相邻两点间测值变化情况，使用较少的数据得到更多的数据信息，得到的数据之间误差较传统回归分析法小，并能正确反映变形规律，具有一定的参考意义。

参考文献：

[1]靳晓光,李晓红,高茺，等.隧道围岩位移的灰色优化模型预测[J].重庆大学学报(自然科学版),2002,25(1):1-5.

[2]乔志超，周建春. 隧道围岩变形监测及分析[J].施工技术,2012, (4):40-42.

[3]HURST H E. Long-term Storage Capacity of Reservoirs: An Experimental Study[J]. Transactions of American Society of Civil Engineers, 1951, 116: 770-808.

[4]GIRAITIS L, KOKOSZKA P, LEIPUS R,etal．Rescaled Variance and Related Tests for Long Memory in Volatility and Levels[J]. Journal of Econometrics, 2003, 112(2): 265-294．

[5]MANDELBROT B B.The Fractal Geometry of Nature[M]. San Francisco, USA: W. H. Freeman and Company, 1982.

[6]DAVIDSON J, HASHIMZADE N. Type I and Type II Fractional Brownian Motions: A Reconsideration[J]. Computational Statistics and Data Analysis, 2009, (53): 2089-2106.

[7]李远耀,殷坤龙,程温鸣.R/S分析在滑坡变形趋势预测中的应用[J]. 岩土工程学报,2010,(8):1291-1296.

[8]贺可强,孙林娜,王思敬. 滑坡位移分形参数Hurst指数及其在堆积层滑坡预报中的应用[J]. 岩石力学与工程学报,2009,(6):1107-1115.

[9]陈学习,宋富美,闫智婕. 基于分形理论的瓦斯涌出规律[J]. 辽宁工程技术大学学报(自然科学版),2012,(5):617-620.

[10]乔美英,陈鑫,兰建义. 基于V/S分析的瓦斯涌出量分形特性研究[J]. 中国煤炭,2014,(10):104-110.

[11]李业学,刘建锋. 基于R/S分析法与分形理论的围岩变形特征研究[J]. 四川大学学报(工程科学版),2010,42(3):43-48.

[12]罗林,左昌群,赵连，等. 基于BP神经网络和R/S分析的隧道仰坡沉降变形预报预测[J]. 施工技术,2014,(11):80-84.

[13]孙洪泉. 分形几何及其分形插值研究[J]. 河北工业大学学报, 2002，(1): 56-60.

(编辑：曾小汉)

收稿日期：2015-01-19；修回日期：2015-03-10

基金项目：国家自然科学基金项目(41202201,41102196,51379194)；中央高校基本科研业务费专项资金项目(CUGL110215)；国土资源部公益性行业科研专项经费资助项目(201211039)

作者简介：左昌群(1981-)，女，湖北荆州人，讲师，博士，主要从事岩土工程研究，(电话)13554111141(电子信箱)helenzz@126.com。

doi:10.11988/ckyyb.20150074

中图分类号：TU94

文献标志码：A

文章编号：1001-5485(2016)04-0051-06

Analysis and Prediction of Tunnel Surface SubsidenceBased on Fractal Theory

ZUO Chang-qun, LIU Dai-guo, DING Shao-lin, LI Lin-sen

(Faculty of Engineering, China University of Geosciences, Wuhan430074, China)

Abstract:The time series of tunnel surface deformation is a nonlinear system with fractal characteristics. According to the surface subsidence monitoring of lion rock tunnel, we calculated the Hurst index of time series of accumulated subsidence and subsidence rate by using the R/S and V/S analysis based on fractal theory. Moreover, we evaluated the stability of surface subsidence, and analyzed the effectiveness of R/S and V/S analysis methods and the non-cyclic period of surface deformation in association with V statistic. We also predicted the surface subsidence values by fractal interpolation function and regression function. Results show that both R/S and V/S analysis methods has good validity for the analysis of time series of surface subsidence. R/S analysis method is prone to be influenced by short-term memory, which makes the result safe; whereas V/S analysis method is more conservative. Three monitoring points will be in stable state for a long time, and the time series of non-cyclic period is about 20 days. Compared with measured value, the error of the predicted value obtained by fractal interpolation is small. The method in this paper could reflect the deformation evolution trend correctly, and is superior to traditional regression analysis.

Key words:ground surface subsidence; deformation time series; fractal theory; Hurst index; fractal interpolation

2016,33(04):51-56