基于改进卡尔曼滤波器的LCL逆变器电流控制

施 烨，吴在军，阚沁怡

（东南大学电气工程学院，江苏南京210096）

基于改进卡尔曼滤波器的LCL逆变器电流控制

施 烨，吴在军，阚沁怡

（东南大学电气工程学院，江苏南京210096）

在对现有逆变器电流环控制策略进行总结基础上，提出在正交坐标系中将卡尔曼滤波器内核嵌入逆变器电流环PI控制器内，从而构成无静差的正弦信号控制器。并对卡尔曼滤波器内核进行改进，将逆变器跟踪误差信号以前馈形式引入到预报误差方差阵中，以提高电流控制器的响应速度。LCL逆变器仿真实验结果验证了所提电流控制方法，具有良好的响应速度和跟踪精度。

电流内环控制；卡尔曼滤波器；LCL逆变器

分布式电源一般需要通过控制灵活的逆变器连接到电网。逆变器控制策略的好坏将直接决定分布式电源的发电效能和运行安全。逆变器控制策略不仅要能满足控制需求，具有较好的暂、稳态性能；而且需要外界提供的参考量要尽量少，算法结构具有一定的通用性。

分布式电源逆变器大都采用纯正弦并网馈电技术，典型的控制策略主要有：PI控制、PR控制、重复控制、无差拍控制、模糊控制和神经网络控制等［1，2］。其中模糊控制依赖于隶属函数的选取，控制精度有待提高；神经网络控制理论体系还不够完善，缺乏系统化的设计方法，实用性不强；无差拍控制具有很好的动态性能和控制精度，但是其鲁棒性不足，且控制器在设计时需要较精确的系统模型；PR控制和重复控制均基于内模原理，理论上可以使逆变器输出无静差跟踪正弦参考信号，但该方法对系统频率变化十分敏感，控制器设计较困难，若设计不当极易引起系统失稳，在设计时需要牺牲跟踪精度来获取稳定性；PI控制是一种经典的控制策略，可以对直流信号进行无静差跟踪，但是对交流信号的控制精度较差。静止同步坐标系PI控制可实现对交流量的无静差控制［3］，但控制器设计需要正弦参考信号，并用Park变换进行坐标系的转换。

卡尔曼滤波器是一种高效率的递归滤波器，它能够从一系列的不完全及包含噪声的测量中，估计动态系统的状态［4］。这种估计方法在信号检测领域已得到广泛的研究，在平稳过程和非平稳过程中均具有适用性，被广泛应用于频率跟踪、谐波分量测量等场合。此外，卡尔曼滤波算法使用递推调用，形式简单、计算量小，十分适合于实时运用的场合［5-7］。

文中提出一种基于改进卡尔曼滤波器的LCL逆变器电流控制方法。利用卡尔曼滤波器对基波正弦信号进行处理，将正弦信号转换为对应的直流信号，再对所得直流分量进行PI控制，以达到对正弦参考信号无静差控制的效果。同时，对卡尔曼滤波器内核进行了改进，将逆变器跟踪误差信号yk以前馈形式引入到Pk预报误差方差阵中，以提高电流控制器的响应速度。基于LCL滤波器的分布式电源并网逆变器的仿真结果验证了所提方法的效果。

1　分布式电源并网逆变器控制策略

光伏电池、风力发电机、微型燃气轮机和蓄电池等分布式电源通常需要通过电力电子装置与常规配电网并网运行［8］。逆变器控制策略主要有PQ控制、下垂控制和VF控制3种［9］。光伏电池和风轮机这类电源输出功率受外界环境影响较大，具有明显的间歇性，通常控制其发出恒定的有功功率或执行最大功率跟踪，为此，一般采用PQ控制；而微型燃气轮机和蓄电池等分布式电源输出功率受外界影响小，既可以控制按照PQ进行控制，又可以采用VF和下垂控制。

工作于PQ控制策略下的逆变器属于电流源型单元，其控制系统如图1所示。图1中Pref，Qref，US分别为参考的有功功率、无功功率和网侧电压，iref与imer分别为电流参考值和采样值，U*为内环产生的调制波信号，L1，L2，C和r分别为LCL滤波电抗、电容和阻尼电阻。通常采用功率外环和电流内环的双环控制。先通过功率外环计算出逆变器输出端口的参考电流，再通过控制逆变器输出电流跟踪参考电流值来达到恒定功率输出的目的。

工作于VF控制策略下的逆变器属于电压源型单元，其控制系统如图2所示。为了提高逆变器跟踪速度，通常采用电压外环和电流内环的控制策略。先通过电压外环计算出内环电流参考值，再通过电流内环控制逆变器输出电流跟踪电流参考值，以达到调节逆变器输出电压的目的。采用下垂控制策略的逆变器，其控制器结构与VF控制类似，主要区别是下垂控制中的电压幅值和频率参考信号不是人为给定的，而是运用系统下垂曲线计算得出的。所以工作于下垂控制策略下的逆变器亦属于电压源型单元，其控制器仍是采用电压外环和电流内环的控制策略。图2中Uref，fref，Umer分别为参考电压幅值、频率和采样电压值，iref，imer，U*，L1，L2，C和r的定义与图1中的定义相同。

图1 PQ控制原理

图2 VF控制原理

综上所述，3种较常用的分布式电源逆变器控制策略虽然外环不尽相同，但是均使用电流内环。因此，对文中所提基于卡尔曼滤波原理改进的控制算法进行验证时，剥离外环控制策略的差异，通过人为设定电流参考值，仅就电流环的控制进行验证，即只对图1和图2中的虚线部分进行研究设计。当电流环工作特性满足要求时，亦说明文中所提算法在PQ、VF和下垂这3种微电网控制策略中均具有适用性。

2　基于改进卡尔曼滤波器的电流控制方法

基于卡尔曼滤波器的的电流控制器原理如图3所示。其设计思路为以参考电流信号为正弦基准，使用卡尔曼滤波器将电流跟踪误差信号中的基频分量转化为直流分量，再将所得直流量输入PI调节器，所得值与经Clark变换后参考电流量做点乘，形成正交电压调制参考量，进而通过SVPWM调制控制逆变器输出。

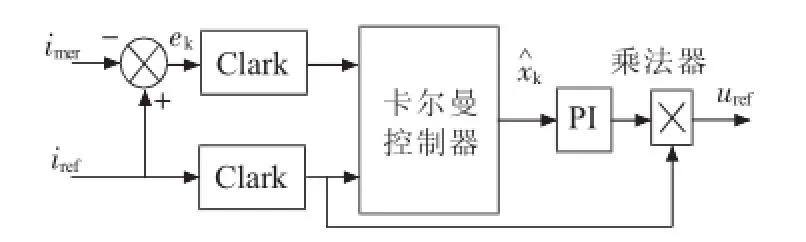
图3基于卡尔曼滤波器的电流控制器原理

为简化分析，设三相三线制系统中的电流参考量分别为iaref，ibref和icref，逆变器跟踪电流误差信号基频分量分别为iam，ibm和icm。首先，通过Clark变换将三相电流参考量和电流跟踪误差转换到αβ正交直角坐标系中。

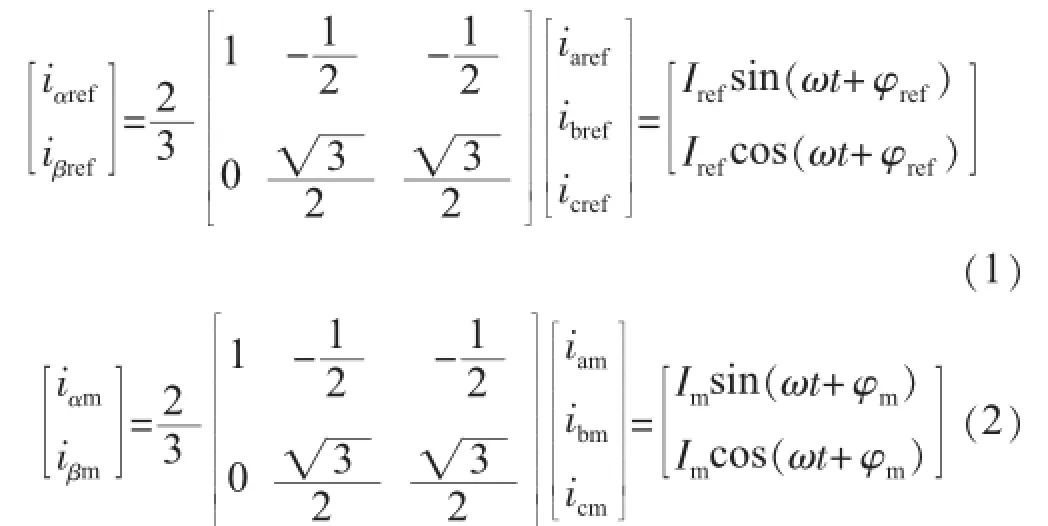
由于iαm和iβm的滤波转换过程具有相似性，文中仅以iαm的直流提取过程为例进行分析。设卡尔曼滤波器的状态空间方程和观测方程分别为：式中：xk为逆变器跟踪误差电流对应的直流分量值为电流跟踪误差信号，即取Ak为单位矩阵为正交坐标参考系，可取为控制干扰信号，其方差为为测量噪声信号，相当于跟踪误差信号中的非基频分量，其方差为Rk。

卡尔曼滤波算法的原理为求取xk的最优估计使得与的均方误差取值最小，即使取到最小值，最终使输出信号趋近于yk中的基频成分。

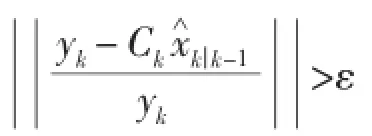
文中将逆变器跟踪误差信号yk以前馈形式引入到Pk预报误差方差阵中，提高系统响应速度。在稳态时，yk将取一个较小量，不影响系统对于参考信号的跟踪精度；参考电流信号突变时，yk将以较大值引入预报误差方差阵更新公式中，从而提高系统的响应速度。

表1卡尔曼滤波算法

3　 LCL参数设计

在逆变器输出端口安装LCL滤波器的主要目的是为改善输出电流波形，消除输出电流在开关频率处的纹波。通常，LCL滤波器逆变器侧电感主要用于抑制开关频率处的谐波，而网侧电感是为了调整LCL滤波器的截止频率。因为LCL滤波器逆变器侧的电感值要大于网侧的电感值，电容值不宜取得太大，以防减低系统的功率因数［11-13］。LCL滤波器参数需要精心设计，设计不当容易引起滤波器衰减阻抗过大，直接降低逆变器效率；或是引起滤波器衰减不充分，容易引起系统不稳。单相LCL滤波器结构如图4所示，其各电量之间的关系如图5所示。

图4 LCL滤波器结构

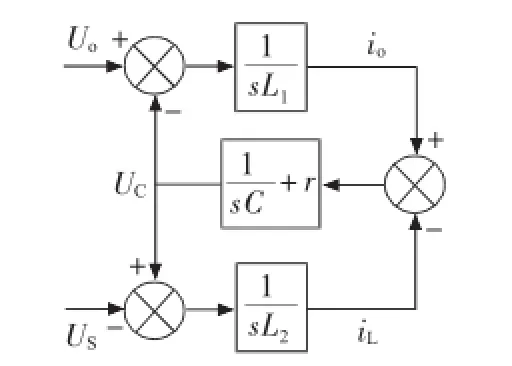
图5 LCL滤波器原理

根据图5，计及负载电阻RL列写LCL滤波器的传递函数为：

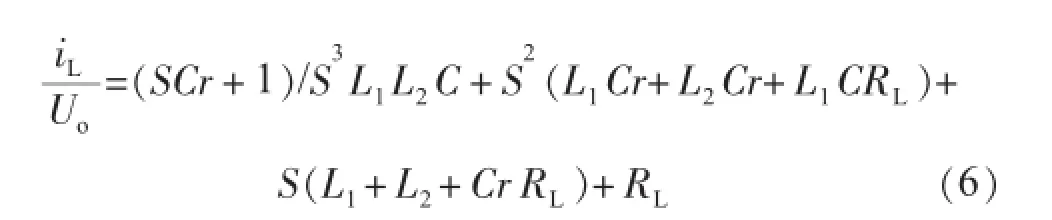
设计LCL滤波器参数如表2所示。

表2 LCL滤波器设计参数

取负载电阻RL=40 Ω，LCL滤波器的波特图如图6所示。

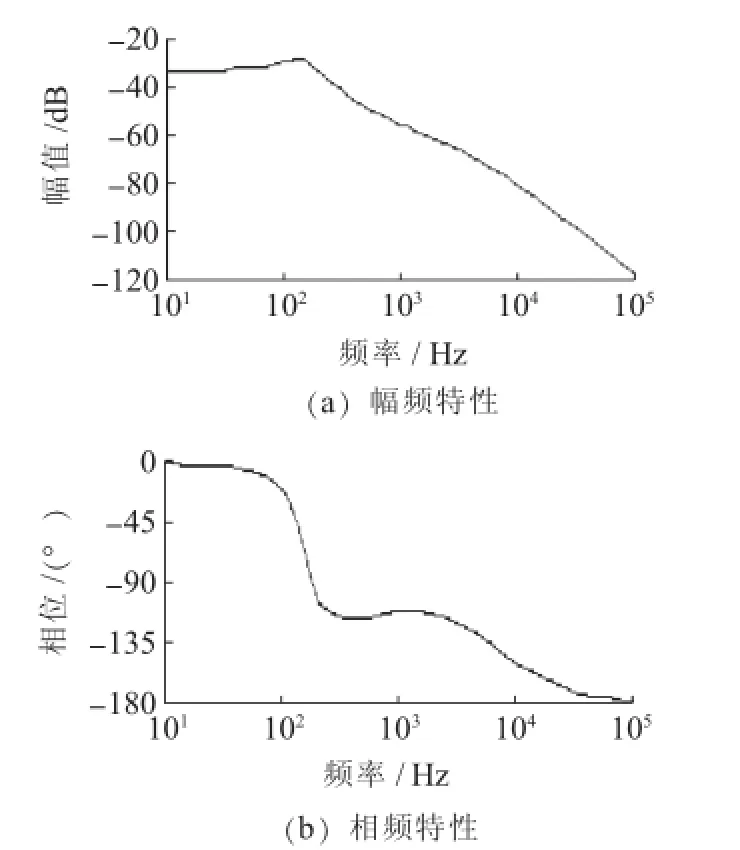
图6离网运行方式下LCL滤波器波特图

当系统并网运行时，负载两端电压将被系统钳位，此时等效为负载阻抗等于0。则此时LCL滤波器的波特图如图7所示。

图7并网运行方式下LCL滤波器波特图

由图6、图7可见，在并网、离网2种工作状态下，LCL滤波器的传输特性存在明显差异。在低频工作区，并网运行时，LCL滤波器呈现电抗器特性；离网运行时，LCL滤波器呈现电阻特性。而在高频区，并离网工作模式下的LCL滤波器均呈现每度-40 dB的高速衰减特性。所以，在设计LCL参数时，需要就并离网状态进行综合考虑。采用文中所述的LCL参数，在低频段具有较小的衰减率，从而保证低频分量的顺利通过；在高频段具有足够的衰减率，可以抑制开关频率处的谐波对输出电流的污染，且消除了LCL滤波器谐振点，保证逆变器运行安全。

为进一步验证所设计LCL滤波器的稳定性，绘制所选参数对应的LCL传递函数，开关频率为12.8 kHz时的根轨迹如图8所示。

图8 LCL根轨迹

由图8可见，在逆变器并网运行时的稳定裕度要远低于离网运行时的稳定裕度。且系统处于轻载状态下的稳定性要低于重载条件下的稳定性。所以为了增强系统的运行稳定性，需要通过有源与无源手段增加系统阻尼，或是通过算法改进来增强逆变器在并网运行时的稳定性裕度。因为卡尔曼滤波器本身具有滤波效果，可以滤除误差信号中的高频噪声，从而保证输出参考电压信号具有很好的正弦度。防止将高频噪声信号再次引入系统，形成噪声信号的正反馈放大，影响系统的运行安全。由于控制器难免会向系统引入延时，系统在增加延时环节后的根轨迹如图9所示。

由图9可见，系统的稳定裕度较未引入延时前将减小，所以需要对延时环节进行补偿。可以利用卡尔曼滤波器的预报功能［14］，对电压参考值做提前一个周期的预报，即此时提供的输出量为从而可以减弱引入延时环节后对系统造成的不良影响。

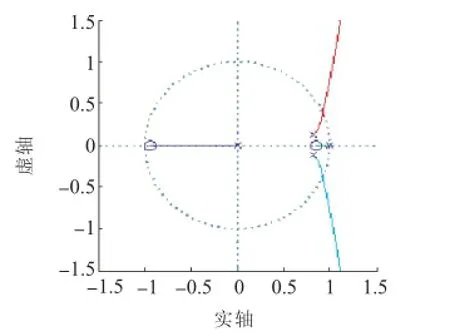
图9引入延时LCL根轨迹

可见，在带LCL滤波器的逆变器中引入卡尔曼滤波器后，将会给逆变器性能带来诸多有益的影响，提高系统稳定裕度。同时，由于卡尔曼滤波器的参考正弦输入量选择为电流内环参考值 iref，由于一般可以保证iref具有较好的正弦度，以iref为卡尔曼滤波器的参考正弦信号并不会影响滤波器的性能。

4　仿真分析

为验证本文所提方法的有效性，在Matlab/Simulink环境下设计了基于改进卡尔曼滤波器的LCL逆变器进行仿真分析。系统线电压为380 V，频率为50 Hz，以阻值为6.4 Ω的电阻来模拟系统负载，逆变器直流母线电压为800 V，开关频率设为12.8 kHz。采用空间矢量调制技术，LCL出口滤波器参数参照上文表2所示。在对所提算法特性进行仿真验证时，从参考信号幅值、频率和相位变化3个方面进行验证。并与带数字锁相环的PQ控制进行对比［15］。在图10中以绿色短虚线表示参考电流波形、以红色长虚线表示PQ控制策略输出a相电流波形、以蓝色实线表示采用卡尔曼滤波原理输出a相电流波形。图10（a）为0.3 s处参考波形的幅值变为原来的2倍。通过比较，可见2种控制方法均能较好地跟踪参考波形的幅值变化。图10（b）为0.3 s处参考波形的相位较原波形滞后60°。通过比较，可见采用卡拉曼滤波原理控制器输出波形超调量要低于采用PQ控制输出波形的超调量。从而证明本文所提控制方法要优于传统控制策略。图10（c）为0.3 s处参考波形的频率变为原来的2倍。通过比较，可见在过零点处参考信号频率变化时，2种控制策略均能很好的跟踪参考电流波形。

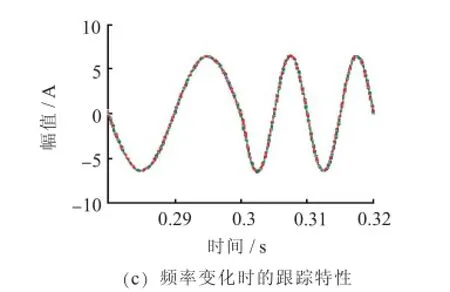
图10控制策略仿真波形

图11为并网状态下，当参考电流的幅值发生变化时逆变器输出电流波形的比较。参考电流峰值在0.3 s时发生突变，由40 A跳变为80 A。其中图11（a）为采用PQ控制策略的LCL逆变器输出三相电流波形，图11（b）为采用卡尔曼原理的LCL逆变器输出三相电流波形。

图11仿真波形比较

由图11可见，采用文中所提方法控制的输出电流波形的调节时间更短，超调量更小，其效果要略优于采用传统PQ控制策略输出电流波形。

5　结束语

提出了一种基于卡尔曼原理的逆变器电流控制策略。直接使用参考电流形成正弦参考信号，省去了设计锁相环的麻烦；采用卡尔曼滤波器滤除控制环路中的噪声信号，保证输出电压参考波形具有较高正弦度，防止对噪声信号进行放大。使用卡尔曼算法提供预测控制，从而提高LCL滤波器稳定性。

［1］蒋震东，李向新.分布式电源并网逆变器控制策略与仿真研究［J］.现代电子技术，2013（3）：142-144.

［2］董 密，罗 安.光伏并网发电系统中逆变器的设计与控制方法［J］.电力系统自动化，2006，30（20）：97-102.

［3］CROWHURST B，EL-SAADANY E F，EL CHAAR L，et al.Single-phase Grid-tie Inverter Control Using DQ Transform for Active and Reactive Load Power Compensation［C］//Power and Energy （PECon），2010 IEEE InternationalConference on，2010：489-494.

［4］OLFATI-SABER R.KALMAN-CONSENSUS F.Optimality，Stability，and Performance［C］//Decision and Control，2009 held jointlywith the 2009 28th Chinese Control Conference.CDC/CCC 2009.Proceedings of the 48th IEEE Conference on，2009：7036-7042.

［5］张 猛，肖 曦，李永东.基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器［J］.中国电机工程学报，2007，27（36）：36-40.

［6］PANOMRUTTANARUG B，LONGMAN R W.Using Kalman Filter to Attenuate Noise in Learning and Repetitive Control Can EasilyDegradePerformance［C］//SICEAnnualConference，2008：3453-3458.

［7］赵丽娜，曹 伟，孙 明，等.带有卡尔曼滤波的灰色补偿PID控制器设计［J］.辽宁工程技术大学学报：自然科学版，2012（6）：881-884.

［8］王成山，肖朝霞，王守相.微网中分布式电源逆变器的多环反馈控制策略［J］.电工技术学报，2009，24（2）：100-107.

［9］王 鹤，李国庆.含多种分布式电源的微电网控制策略［J］.电力自动化设备，2012，32（5）：19-23.

［10］郭文勇，肖立业，郭金东，等.动态电压恢复器的最优控制和最优滤波［J］.中国电机工程学报，2009，29（6）：48-54.

［11］黄宇淇，姜新建，邱阿瑞.LCL滤波器在三相PWM整流器中的应用［J］.电力自动化设备，2008，28（12）：110-113.

［12］TEODORESCU R，BLAABJERG F，LISERRE M，et al.A Stable Three-phase LCL-filter Based Active Rectifier Without Damping ［C］//Industry Applications Conference，2003 38th IAS Annual Meeting.Conference Record of the，2003：1552-1557.

［13］LISERRE M，DELL'AQUILA A，BLAABJERG F.Stability Improvements of an LCL-filter Based Three-phase Active Rectifier ［C］//Power Electronics Specialists Conference，2002.pesc 02. 2002 IEEE 33rd Annual，2002：1195-1201.

［14］AHMED K H，MASSOUD A M，FINNEY J，et al.Sensorless Modified Adaptive Kalman Filter for Current Control of a Threephase Inverter Based Distributed Generation［C］//Industrial Electronics，2008.ISIE 2008.IEEE International Symposium on，2008：1592-1597.

［15］XU J P，GUANn R Q，LIU J Y.The PID Control Based on Nonlinear Adaptive Kalman Filter［C］//Electrical and Control Engineering（ICECE），2011 International Conference on，2011：2722-2725.

A Current Controller for LCL Inverter Based on Improved Kalman Filter

SHI Ye，WU Zaijun，KAN Qinyi
（School of Electrical Engineering，Southeast University，Nanjing 210096，China）

After reviewing the existing current control methods for inverters，an improved Kalman Filter based current control method is proposed in this paper.In this method，the Kalman Filter kernel is applied to the PI controller in the orthogonal reference frame，which results in a sine current controller without steady error.To improve the dynamic of the proposed current controller，the inverter current tracking error is feedforwarded to the forecast error variance matrix.The simulation results show that the proposed current control method has a good response speed and tracking accuracy.

inner current control loop；kalman filter；LCL inverter

TM464

A

1009-0665（2016）01-0028-05

2015-10-26；

2015-11-20

施烨（1988），男，江苏南通人，博士研究生，研究方向为分布式发电与微网、电能质量分析与控制；

吴在军（1975），男，江苏南京人，博士生导师，研究方向为变电站自动化、分布式发电与微网、电能质量分析与控制；

阚沁怡（1993），女，江苏南京人，硕士研究生，研究方向为分布式发电与电能质量。