考虑风电预测误差的电力系统有功实时调度
张文婷,范立新,顾 文
(1.东南大学电气工程学院,江苏南京210096;2.江苏方天电力技术有限公司,江苏南京211102)
考虑风电预测误差的电力系统有功实时调度
张文婷1,范立新2,顾文2
(1.东南大学电气工程学院,江苏南京210096;2.江苏方天电力技术有限公司,江苏南京211102)
针对风电预测误差对实时调度的影响,研究相应的实时调度策略,提出一种考虑风电预测误差的电力系统有功实时经济调度方法,优化缓冲机组出力。使用拉普拉斯分布描述风电预测误差随机分布特性,基于拉丁超立方采样的概率潮流方法求解系统有功潮流概率分布,以经济性最优与弃风最小为目标,引入机会约束条件,建立考虑风电预测误差的缓冲机组有功最优分配模型,并采用改进的遗传算法求解该机会约束规划模型。最后在IEEE24节点系统中验证了模型和方法的可行性,结果表明,在实时调度中考虑风电预测误差,能够保障系统的安全运行,提高系统接纳风电的能力。
实时调度;风电预测误差;概率潮流;机会约束;改进的遗传算法
电力系统经济调度问题以经济型最优为目标,满足系统功率平衡和运行约束条件的优化问题。由于现有的风电预测精度较低,当大规模风电并网时,风电波动造成的功率缺额将会给电网的安全运行带来威胁。文献[1]提出“多级协调、逐级细化”的思路,将控制分为4个阶段:日前调度、滚动调度、实时调度和AGC,使得上一级遗留的偏差由下一级修正。实时调度取系统中性能良好,爬坡速率较快的机组为缓冲机组,是在滚动调度基础上的进一步校核和修正,本质上是对缓冲机组出力的动态优化问题。文献[2,3]研究含大规模风电实时调度模型,仅考虑到负荷预测的偏差,忽略了风电预测误差。负荷预测虽然存在误差,但相较于风电预测,其变化趋势认为是可以被精确预测的[4]。风电预测的实测值与预测值之间存在较大差异,影响实时调度结果和系统安全。所以文中针对风电预测误差对实时调度的影响,研究相应的调度策略。
现有实时调度算法中计算系统有功潮流分布,普遍采用线性化方法[5],引入负荷平衡灵敏度算子,存在一定的误差。概率潮流算法通过在潮流计算中考虑各状态变量的不确定性,能够准确地获得节点电压和线路潮流等的概率分布。文中采用基于拉丁超立方采样的概率潮流算法,可以在不显著增加计算次数的同时,有效地提高计算效率[6]。此外,由于存在随机变量,文中采用机会约束规划方法建立缓冲机组有功最优分配模型。
1 考虑风电预测误差的概率潮流计算方法
1.1风电预测误差
令W(t)为风电的预测值,则相应预测误差为:

式中:εf(t)为t时刻风电场的实际输出与其预测值的误差。Wf(t)一般代表预测分辨率上的平均值。随着预测时间尺度的变小,εf(t)绝对值的期望值将越来越小。
文献[4]发现在较小的时间尺度上(1 h以内),风电的预测误差序列是独立同分布的,而且εf(t)服从拉普拉斯分布,其概率密度函数为:

式中:λ为尺度参数,通过大量风电出力偏差数据可以拟合风电预测误差的概率密度函数,从而与拉普拉斯分布比较得到参数λ,λ>0。拉普拉斯分布函数如图1所示。

图1拉普拉斯分布
1.2基于拉丁超立方采样的概率潮流计算方法
拉丁超立方采样作为一种分层采样法,其采样值能有效反映随机变量的整体分布,计算效率较高。其基本步骤如下。
(1)采样(如图2所示)。设x1,x2,…,xN是待求解的N个随机变量,其中xi(i=1,2,…,N)的概率分布函数为:
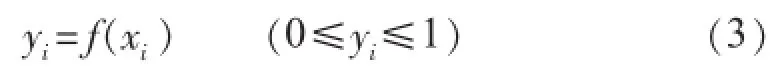
设K为采样数,将曲线yi=f(xi)的纵坐标等分为K段,第k个采样区间对应xi的采样值为:
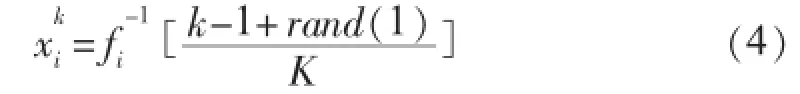

图2拉丁超立方采样示意

图3双时间尺度有功协调控制框架
基于上述方法将每个随机变量的采样值依次在矩阵中排成一行,可以得到N×K维采样矩阵X。
(2)排列。首先形成一个阶的顺序矩阵C,并采用该矩阵中的元素值表示采样矩阵X相应元素所处的位置。矩阵X元素按照顺序矩阵C的位置进行排列得到最终的采样矩阵X'。文中采用文献[7]中计算顺序矩阵C的Gram-Schmidt序列正交化方法,能够最大程度的降低随机变量的相关性。
文中关注的是系统有功潮流变化,故采用直流潮流算法,系统节点注入有功功率矩阵表达式为:

式中:P和θ分别为n-1阶节点有功功率注入和电压相角向量;B'为常数矩阵,由节点导纳矩阵的虚部计算得到。依据拉丁超立方采样对风电预测误差随机变量进行采样后计入相应节点,通过数学统计得到线路有功潮流的概率分布。相对于传统线性化方法,概率潮流计算能够比较全面地反映风电预测的不确定性带给系统的扰动,同时原理简单,使结果更具有可解释性和鲁棒性。
2 系统模型
2.1 双时间尺度有功协调控制框架及其不足
研究文献[1]提出的双时间尺度有功协调控制框架下的实时调度模型,依据风电的预测精度随着时间尺度的变小而逐级提高的特性,建议在ACG与日前调度之间加入实时调度和滚动调度。滚动调度启动周期为30 min,动态的对日出力计划曲线进行修正。实时调度以15 min为周期,依据提前15 min的预测信息调整缓冲机组的出力并提前15 min下发给对应机组,修正滚动调度结果。由于在滚动调度之后,实时调度所需修正的机组出力的量相对较小。其框架结构如图3所示。
然而,大规模风电并网时,由于风电预测方法的局限与风电的随机特性,风电预测误差造成的功率缺失无法满足调度的需求,影响系统的功率平衡与潮流稳定,需要切除部分负荷或采用其他手段来平衡有功功率。此外,受到传统机组爬坡速率的限制,风电多发时,可能带来不必要的弃风。考虑风电预测误差后调整电网的实时调度计划,对电网的安全稳定运行有着实际意义。关于滚动调度具体模型文中不涉及,基于文献[1]滚动调度算法结果进行实时调度优化。
2.2考虑风电预测误差的实时调度优化模型
大规模风电并网的实时调度计划应以尽可能地接纳风电为前提,同时考虑调度的经济性。
(1)优化目标。设置阈值Pwind,当风电预测出力变化小于Pwind时,全部接纳风电,目标函数为:

式中:Nrt为缓冲机组的集合为缓冲机组v发电出力单位调整成本为缓冲机组v在t时刻初的出力调整量(在t-1时刻计算并下发)。当风电预测出力增量大于Pwind时,目标函数变为:

式中:Nwind为风电机组的集合(t)为风电机组v在t时刻初的弃风量;κv为弃风权重因子。
大部分情况下,实时调度阶段弃风量为0,设置阈值Pwind可以在风电预测出力变化较小,系统能够较好地消纳风电的情况下,减少变量规模与智能算法寻优时间,提高计算效率。因此,Pwind值不固定,取值与调度结果没有相关性,通过事前仿真可以确定 Pwind的范围,为了增强调度结果的可靠性,一般Pwind取值较小。
(2)缓冲机组整体出力约束。
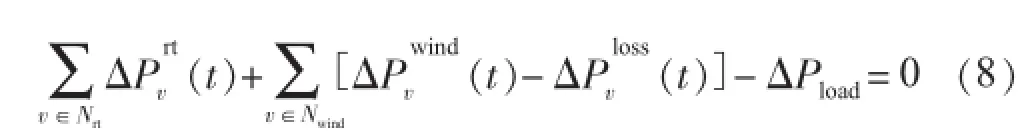
式中:ΔPwindv(t)为风电机组v预测出力的变化量;ΔPload为总负荷预测变化量。(3)线路潮流约束。

(4)缓冲机组出力调整上下限约束。

(5)备用容量约束。

式(6—11)为计及风电预测误差的机组有功实时调度优化模型。模型将风电预测误差视为一变量引入式(9)与(11),确定约束形式不再适用,因此采用机会约束形式。
2.3模型求解
由于2.2节中建立机会约束规划,约束中包含随机变量,无法运用确定性方法验证。文中采用改进的遗传算法[8]进行求解,比较于基本遗传算法增加了保留操作,即将上一代种群中的若干最优染色体直接复制到本代。步骤如下:
(1)读取系统网络数据及机组参数;
(2)读取最新滚动调度后系统中机组出力;
(3)设置阈值Pwind,根据最新获取的负荷预测和风电预测结果,判断风电出力增量是否超出Pwind。若超出,则考虑弃风,否则系统全部接纳风电出力;
(4)设定缓冲机组出力调整量和弃风量为决策变量,组成待求染色体;
(5)随机产生初代染色体,基于拉丁超立方采样获取风电预测误差样品,通过概率潮流方法得到系统有功潮流概率分布,验证其是否满足约束条件。若满足约束,则放入初代种群,否则重新产生染色体,直到到达种群规模N;
(6)经由改进的遗传算法中选择、保留、变异、交叉、复制和选择操作,采用基于序的评价函数,对新产生种群进行检验以确认其是否满足约束,直到指定代数或满足收敛性条件:
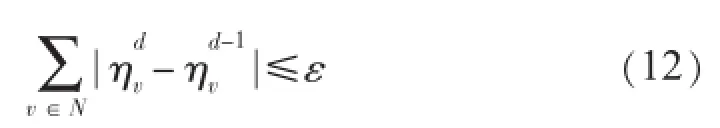
(7)最终代染色体中最优个体即为优化后系统缓冲机组出力调整量和弃风量。
算法流程如图4所示。
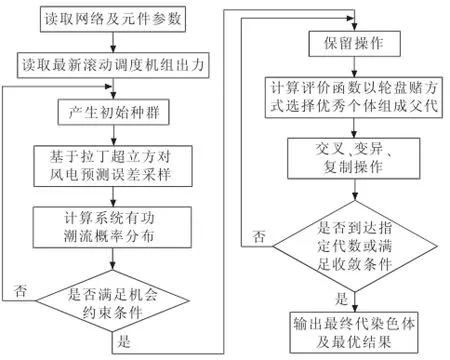
图4算法流程
3 算例
采用IEEE24节点系统作为算例,系统的网络拓扑结构如图5所示,具体系统参数见文献[9]。负荷数据、发电机费用等参数见文献[10]。文献[10]有1 d 24个负荷数据,在此基础上插值生成96个时段的负荷数据。缓冲机组为第21、22、23、24、25、26号机组,缓冲机组出力最大调整量为其最大出力的30%。
风电场的接入点为1、2、7、15、16、23号节点,每个接入点处的风电容量占风电场总出力的百分比分别为15%,15%,15%,15%,20%,20%。每个风电场提前15 min的风电预测误差均服从拉普拉斯概率分布,相应概率密度函数的参数λ均为38.22。使用ERCOT数据库中的风电数据库产生96时段风电预测信息,原始预测信息的分辨率为15min。
实时调度以15 min为间隔,将1 d分为96个时段,在MATLAB仿真后,得到96时段实时调度缓冲机组出力调整情况。仿真中置信水平设置为0.05,保证了系统的潮流稳定和功率平衡。由于各缓冲机组变化趋势相同,以机组24为例进行说明。图6为考虑风电预测误差前后缓冲机组24的出力变化。从图中可以看出,考虑风电预测误差后24号机组出力范围为160~340 MW,均没有超出相应机组出力的上下限。虽然考虑风电预测误差前后机组出力的总体趋势一致,但是局部会存在较大差异,其中最大偏差到达27 MW。图7为考虑风电预测误差前后缓冲机组24出力调整上下限对比。从图中可以看出,考虑风电预测误差后,大部分情况下24号机组出力调整上下限均得到拓展,最大达到上限上调26.58 MW。通过文中提出的实时调度方法,重新调整缓冲机组间出力,缓冲机组获得了更多调整空间消纳风电预测误差,可以为应对风电出力偏差留下更加充分的双向调整裕度。
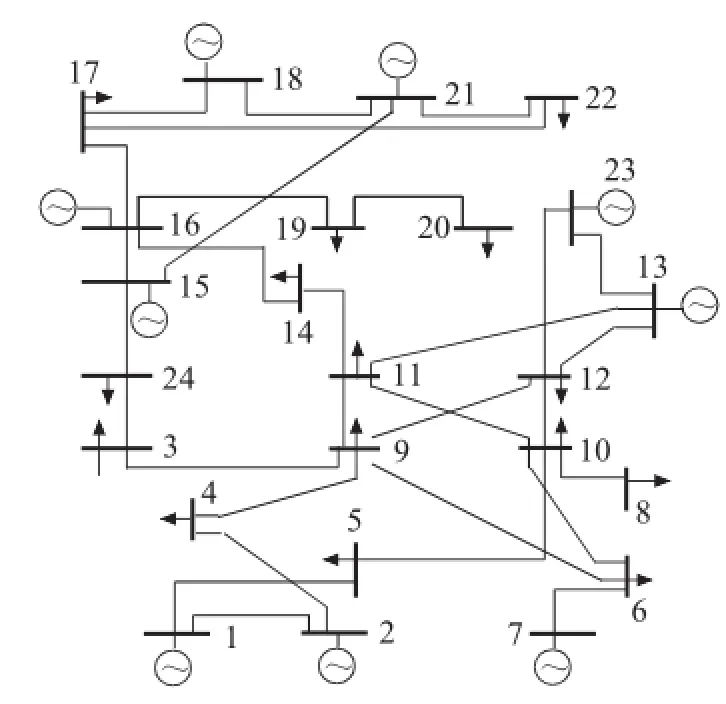
图5 IEEE24测试系统
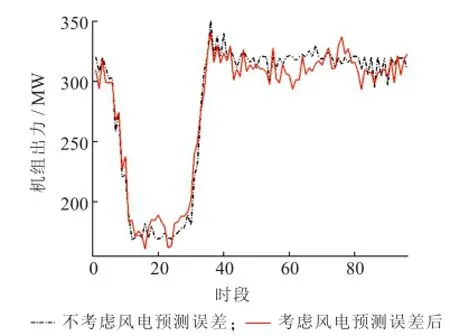
图6机组24出力对比

图7机组24出力调整上下限对比
由于算例中系统引入的风电场容量不大,且依据风电预测出力信息,每15 min风电出力变化较小。依据文中实时调度模型,当风电预测出力变化小于Pwind时,风电全部被接纳。为了保证实时调度结果的可靠性,选取较小的阈值Pwind。本例中取Pwind=15 MW。仿真结果与不考虑风电预测误差弃风对比,不考虑风电预测误差时,弃风量为42.531 6 MW,考虑风电预测误差后,弃风量减为26.333 6 MW。由此看出,考虑风电预测误差后,弃风量显著下降。这是由于缓冲机组在消纳风电出力偏差的同时,也为下一时段的风电预测出力的改变做好准备,提前调整好缓冲机组出力的分配,尽可能地接纳风力发电,系统接纳风电变化容量增大。
由于实时调度时间间隔较短,对调度算法计算时间有较高要求。图8为算例在96时段仿真中的用时变化曲线。统计得到算法所需平均计算时间为45.008 1 s,说明文中算法有着很好的计算效率,能够满足在线实时调度的要求。
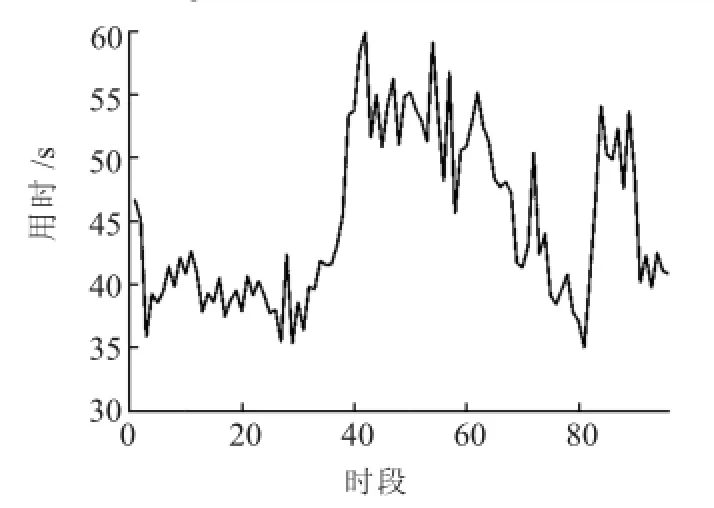
图8仿真用时变化曲线
4 结束语
针对风电出力预测的不确定性,提出了一种考虑风电预测误差的电力系统有功实时调度方法。采用满足拉普拉斯分布的风电预测误差模型,建立满足系统约束和机组约束的机会约束规划,采用概率潮流方法验证网络安全约束,从而对缓冲机组出力进行优化,通过IEEE24节点系统作为算例验证了方法的可行性。考虑风电预测误差后,能避免风电预测可能存在的较大误差对系统运行的影响,保证系统的功率平衡与网络安全约束,合理调整系统的调度计划,使得缓冲机组获得更多调整裕度,还可以提高系统接纳风电的能力。
[1]张伯明,吴文传,郑太一,等.消纳大规模风电的多时间尺度协调的有功调度系统设计[J].电力系统自动化,2011,34(1):1-6.
[2]王 魁,张步涵,周 杨,等.基于混沌量子粒子群算法的含风电场电力系统实时调度[J].电力系统自动化,2012,35(22):141-146.
[3]李 扬,葛 乐,林 一.电力市场下计及节能环保的实时发电调度策略[J].电力自动化设备,2009,29(3):42-45.
[4]SU H I,EL GAMAL A.Modeling and Analysis of the Role ofEnergy Storage for Renewable Integration:Power Balancing[J]. Power Systems,IEEE Transactions on,2013,28(4):4109-4117.
[5]周劼英,张伯明,尚金成,等.河南电网实时调度系统若干功能与算法[J].电力系统自动化,2006,30(2):99-104.
[6]张沈习,程浩忠,张立波,等.含风电机组的配电网多目标无功规划[J].电力系统保护与控制,2013,41(1):40-46.
[7]于 晗,钟志勇,黄杰波,等.采用拉丁超立方采样的电力系统概率潮流计算方法[J].电力系统自动化,2009,33(21):32-35.
[8]韩学栋,王海华.基于遗传算法的有源电力滤波器直流母线电压控制[J].江苏电机工程,2014,33(1):14-17.
[9]SUBCOMMITTEE P M.IEEE Reliability Test System[J].IEEE Transactions on Power Apparatus&Systems,1979(6):2047-2054.
[10]WANG S J,SHAHIDEHPOUR S M,KIRSCHEN D S,et al. Short-term Generation Scheduling with Transmission and Environmental Constraints Using an Augmented Lagrangian relaxation[J].Power Systems,IEEE Transactions on,,1995,10(3):1294-1301.
Real-time Active Power Dispatch of Wind Integrated System Considering Wind Power Forecast Errors
ZHANG Wenting1,FAN Lixin2,GU Wen2
(1.School of Electrical Engineering,Southeast University,Nangjing 210096,China;2.Jiangsu Frontier Electric Power Technology Co.Ltd.,Nanjing 211102,China)
Considering the influence of wind farm forecast errors on real-time dispatch,this paper studies corresponding dispatch strategy.A real-time dispatch model to optimize the output of generators for wind power integrated system is proposed.In this model,forecast error is considered and Laplace distribution is used to describe the density function of wind power forecast errors.A chance constrained program based on probabilistic load flow is built using Latin sampling methods. An improved genetic algorithm is adopted to solve the chance constrained program model.Lastly,the simulation on IEEE24 system proves the viability of the model.It demonstrates that taking forecast errors into accounts can guarantee the power balance and load flow safety of system.Also,it is able to enhance the ability of accepting wind power for wind integrated system.
real-time dispatch;wind power forecast errors;probabilistic load flow;chance constrained;improved genetic algorithm
TM614
A
1009-0665(2016)01-0011-05
2015-08-21;
2015-10-27
国家863高技术基金项目(2011AA05A105);国家电网公司重点科技项目(NY71-13-037)
张文婷(1991),女,江苏徐州人,硕士研究生,研究方向为可再生能源在电力系统中的应用;
范立新(1966),男,安徽巢湖人,高级工程师,从事继电保护和新能源研究工作;
顾文(1969),男,江苏南京人,高级工程师,从事为电厂及新能源技术监督和试验工作。

