工业控制系统重要节点的快速挖掘

张　醒　 徐建平

(华东理工大学信息科学与工程学院1，上海　200237；上海工业自动化仪表研究院2，上海　200233)



工业控制系统重要节点的快速挖掘

张醒1徐建平2

(华东理工大学信息科学与工程学院1，上海200237；上海工业自动化仪表研究院2，上海200233)

摘要：工业控制系统的可靠性、稳定性、抗毁性是工控系统安全首要问题。为提高系统安全性，提出了快速挖掘工业控制系统中重要节点的方法。针对工业化和信息化的深度融合的大型复杂工控系统，采用了基于复杂网络理论的重要节点评估思想。鉴于工业系统的特有节点分布不均衡性和社团性、有机结合度中心性、K-壳及社团扩散性，提出ER+方法，对实际挖掘样本进行分析。利用SIR动态分析试验，证明了该方法更加准确有效稳定。

关键词：工业控制系统ER+SIR可靠性安全性工业化信息化信息安全

0引言

工业控制系统(industrial control system,ICS)包括监控和数据采集(supervisory control and data acquisition,SCADA)系统、分布式控制系统(distributed control system,DCS)和其他控制系统[1-2]。然而随着工业化与信息化的深度融合及智能化的工控系统在基础行业和政府公共事业的重要性比重增大,以及工控系统越来越大型化、复杂化[3],信息安全对于工控系统的威胁越来越大。因此，当前迫切需要进行研究，并及时提出解决新型问题的方法。

对于工控系统复杂化、大型化问题，可以引入复杂网络理论来处理。将整个系统网络的有信息流动部件进行节点化处理，认为所有部件都是一致相似的，组成网络拓扑图，特别是工业控制系统具有一定的结构分布性(社团性)。怎样有效地评价网络节点的可靠性和重要性非常重要。由于自然因素、设计因素及蓄意攻击，工控部件可能发生故障失效，对系统的可靠性造成影响。网络中只要有少量节点发生问题，就会影响整个系统安全。例如攻击一个无标度网络，仅少量重要节点失效就会导致整个网络瘫痪[4]。怎样对这些重要节点评估和节点排序是个重要课题。现实中当多个部件同时发生故障时，考虑维护顺序，可以使系统遭受的损失最小；系统构建时，优化系统网络拓扑结构，可大大提高系统抗毁性。

本文针对工控系统特有属性，提出一种基于网络的社团结构划分、度值及K壳的方法。该方法综合了全局与局部及社团结构特点，可以挖掘工业控制系统中的重要节点。

1理论基础与各种方法

1.1网络模型与理论

(1)

式中:aij为节点i与节点j的连接。

节点的度值Ki等价于节点i与其邻接节点相连数目，度中心性(DC)认为度值越大，其重要性越大[5]。节点距离d指的是任意两节点直接的最短路径边数，假如两节点i、 j不相通，则dij→。

1.2重要节点评估方法

为提高系统可靠性和容错抗毁性，采取挖掘有影响力节点的方法。它提供了一个理解工控系统安全的新视角。节点评估的方法有很多种，主要是通过中心性衡量的，主要分节点邻接性、路径、特征向量等几种方式。

本文只考虑以下几种。度中心性是较简单、也较常用的方法，认为节点i连接边数越多就越重要,但是一个局部环境信息，没有考虑全局(更高阶邻接节点)。接近中心性(CC)[6]节点i与其他节点距离的平均值越小越重要，但其时间复杂度高。介数中心性(BC)[7]通过节点i的最短路径越多就越重要，但其时间复杂度也很高。K-壳分解法[8]由Kitsak等人提出，认为节点重要性与节点所处的位置有很大的关系，核心位置(即使度很多小)也可以拥有很大的影响力，但属粗粒度方法。

1.3挖掘社团结构方法

社团结构是复杂网络最重要和最具代表性的结构属性之一，网页主题、蛋白质网络、社交网络中有很多应用，同时工业控制系统也含有大量社团结构，它对分析复杂网络各种特性起着很重要作用。社团内部连接比较紧密，共享一些特有属性，而各社团之间连接比较稀疏[9]。

整体对于社团结构的挖掘方法主要有基于模块度指标和层次分析及重叠性法[10]。前者是通过不断合并结点的方式，直接优化模块度Q值来获得网络的社团结构划分。

(2)

目前，学术界对于模块度指标可采用自底向上的聚合思想、自上向下的分裂思想、直接寻优的方法。而层次分析及重叠性指网络可能具有不同层次的组织结构，社团中包含社团，可用凝聚算法，其能够很好地区分层次结构，但计算量过于复杂。

2算法提出

2.1总体思想

工业控制系统构成的拓扑图节点分散，呈现很大稀疏性，为完成不同的任务会有不同结构分布，例如现场网络层 (fieldnetwork)、控制网络层 (controlnetwork)、监控网络层 (supervisionnetwork) 和管理网络层 (managementnetwork)等组成工控系统网络。所以，不能简单、直接地引用普通的节点评估，这样不能体现系统节点多样性；但是也不能挖掘网络社团结构，直接将系统网络分割开来分析，这会严重破坏系统完整性，对节点评估会产生严重误差。因此，本算法采用社团结构和节点评估有机结合的方式。

2.2社团算法思想

本文不直接采用社团结构属性，而是利用节点社团扩展性[11](communitydegree,CD)，即每个节点的邻接节点所属不同型数目的社团，以表现连接社团多样性。其值越大越好。

社团挖掘算法有很多，但是要符合工业控制系统拓扑要求，即不仅能处理层次化社团结构，而且也能精确高效地处理大型工业控制系统(大型复杂网络)，故综合选择知名的凝聚算法BGLL[12]。该算法是由VincentD.Blondel提出的。

该算法分成两个阶段反复迭代。第一阶段把每个节点当作一个社团，把任意节点i移出自己所在社团，并放置在其邻接节点的社团。根据式(2)计算其邻接节点对应的模块度增量ΔQ为:

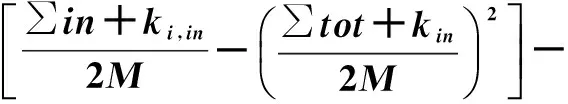
(3)

式中：∑in为社团C内部度值之和；∑tot为与社团C内部所有节点有链接度值和；ki为节点i的度值；ki,in为节点i与C社团内所有度之和；M为邻接矩阵度和。若ΔQ为正值，应选择对应邻接点最大ΔQ值的社团，把节点i放置其中；反之ΔQ值都为负数，选择将节点i依旧放在原来社团。这个过程节点不停转移、重复，直至所有节点位置不发生变化，此过程结束。

第二阶段是建立一个新的网络。依据第一阶段挖掘的社团，新节点连接等于原各社团之间所有节点之间边权和，在构造好新网络后可采用第一阶段再次挖掘社团，得到第二层社团。依次类推，直到不能产生大模块，算法结束。这样获得每个节点所在社团位置，再利用邻接矩阵可获得每个节点的社团扩展性。美国高级研究计划署(advancedresearchprojectagency,ARPA)网络拓扑图如图1所示，含21个节点、26条边。网络中节点19、节点12、节点3都连接三个不同的社团，但不能由此细分以上三个节点的重要性，需要结合一般节点的评估方法来判断。

图1　ARPA网络示意图Fig.1　ARPA network

2.3社团结构与节点评估方法有机结合

考虑到网络社团扩展性CD算法不够精确，引入了度中心性DC、K-壳Ks，主要考虑度中心性DC直观描述节点局部性，该方法计算度低；K-壳Ks描述节点位置在网络核心还是边界[8]，具体分解是移除网络存在度1的节点和边,再检查网络中是否还含有度1的点和边并去除，直到网络中没有度1的节点，这些去除节点为Ks=1，依次类推可获得其他Ks；另一方面，由于三者的相关性不是很大[13-14]，故可以有机结合。

由于三者会有不同量纲，所以须作归一化处理。对取得的归一化数值采用欧拉公式处理，获得全局参数的计算式为AD：

(4)

AD越大越好。为了使结果更加精确，可以再次利用节点邻接性，获得最终的节点评估结果ER+。

(5)

(6)

式中:AD(S)为节点i的邻接点的全局参数AD。

2.4算法描述

下面给出节点重要度评估方法的简单算法步骤。

输出：节点关键度ER+(i)。

①计算所有节点的度值Ki、K-壳Ksi;

②利用BGLL方法挖掘网络所有节点的社团，即式(2)、式(3)，通过邻接矩阵获得社团扩展性CDi；

③分别归一化以上三种节点属性，利用欧拉公式计算所有节点的全局参数ADi，即式(4)。

④通过节点邻接性，利用式(5)、式(6)，得出节点重要度评价结果ER+(i)。

3试验及分析

3.1数据

为了评估算法有效性，引入真实开放的数据。考虑到现实世界网络复杂性多样性，特采用两组数据：一组小数据，即美国ARPA网络，它代表小型、连通、均匀的网络；另一组数据采用美国西部电力网络数据，包含4 941个节点、6 594条边，其代表大型复杂、分布广泛、非全连通、非均匀的网络。

3.2SIR评估试验数据

在试验中采用了在复杂网络中验证节点影响力常用的方法SIR，来提高试验结果可信度。SIR模型是作为疾病或信息传播模型，每个节点处在以下三个状态中的一个：S易感染状态、I感染状态、R移除状态。在每个时间步长内，感染的节点以β的概率去感染它的邻接邻居中的易感染者，同时感染节点再以γ的概率移除(死亡或产生免疫)。

为减小时间计算复杂度，令γ=1，而β通常比其邻接矩阵的最大特征值倒数稍大(过大所有节点信息传播面大都体现不了算法优越性，过小会使传播体现在极小局部范围)。只要β/γ值不变，则结果不会发生变化。

为提高计算精确度，采用完全基于邻接矩阵的SIR模型[14]，具体公式如下：

(7)

(8)

(9)

式中：NJ为节点i的邻接节点集；β为感染率；r为恢复率。

开始将目标节点作为感染状态，其他节点为易感染状态，目标节点向周围节点传播信息，直至网络所有节点状态变化趋于稳定，没有感染状态，此动态过程停止。最终信息传播覆盖面积(R状态数目)表现为节点影响力大小，其面积越大，则表示节点影响力越大；反之亦然。

先对美国ARPA网络进行分析，对度中心性DC、介数中心性BC、K-壳分解法、接近中心性CC作比较，以SIR为参考标准，表1是其各种方法运算的节点重要度排名(K-壳运算都是4壳，无法排名)。从表1中可以明显看出，本文ER+算法与SIR信息传播近似度最大。同时也可看出CC、BC全局性算法结果也不错，DC算法也取得不错效果。美国西部电力网络比较均匀且是全连通图，所有节点的各种属性几近相同，对各种方法不是很敏感。相关分析表明，节点3度值为4，且社团扩展性为3处在所有节点最大值，故排名高。而节点14、2的度值为4，社团扩展性为2，所以排名紧靠节点3。故该算法明显优于其他只考虑节点某一方面的算法。

表1　PA网络节点重要度前10排名Tab.1　Ranking of the top10 vertices of the ARPA network

对美国西部电力网络进行分析，由于节点过多，不可能对所有节点都进行SIR信息传播，这样既费时，又体现不了对比方法的优越性，所以只考虑对各种方法节点重要度排名前20名、50名及100名与ER+前20名、50名及100名的不同节点作SIR分析。例如度中心性与本方法前5名分别为{100、2、4、67、23}、{3、100、23、78、9}，只分析度中心性{2、4、67}和本方法{3、9、78}，F(t)代表移除状态和感染状态与节点总数的比随时间的变化曲线。图2分别为ER+与介数中心性BC、接近度中心性CC、度中心性DC、K-壳Ks分解法获得前L排名节点，通过SIR分析的对比结果。由图2可以发现：ER+与其他各种方法相比，具有特别好的效果；同时看出全局性方法表现最差，也证实了式[8]中介数中心性、接近中心性在一些特殊网络中表现较差；度中心性也没有衡量节点位置，表现也较差；K-壳虽然考虑位置，表现强于以上三种方法，但是忽略邻接节点及社团结构，与ER+相比还是存在一定差距。

图2　ER+与BC、CC、DC、Ks前排名L节点的F(t)曲线Fig.2　F(t) for top-L ranked nodes by ER+,BC,CC,DC,Ks

综上分析可知：ER+能很好地处理小型、大型，连通、非连通网络，均匀网络、非均匀网络。因此，ER+方法可以处理这种节点多分布广泛且含有社团结构的大型工业控制系统网络。

4结束语

本文首次提出利用系统拓扑图快速寻找工控系统有效重要节点，以提高系统快速修复能力和容错抗毁性。通过借鉴复杂网络理论并结合工控系统实际情况，提出了ER+重要节点评估法。通过SIR信息传播，证明该方法的可行性，该方法优于其他局部方法或全局方法，适用于大型社团化、分布广泛的工控系统。

参考文献：

[1] 卢慧康.工业控制系统信息安全风险评估量化研究[J].自动仪表,2014,35(10): 21-25.

[2] 陈维刚,费敏锐.工业控制系统的网络化发展[J].工业仪表与自动化装置,2004,1(1):10-13.

[3] 韩晓波．企业工业控制网络安全技术探讨及实现[J]．化工自动化及仪表,2012,39 (4)：498-499．

[4] ALBERT R.Error and attack tolerance of complex networks [J].Nature,2000,406(6967):378-382.

[5] BONACICH P.Factoring and weighting approaches to status scores and clique identification[J].Math SOCIOL,1972,2(1): 113-120.

[6] FREEMAN L C.Centrality in social networks conceptual clarification[J].SocNetw,1979,1(3): 215-239.

[7] FREEMAN L C.A set of measures of centrality based on betweenness[J].Sociometry,1977,40(1): 35-41.

[8] KITSAK M,GALLOS L K,HAVLIN S,et al.Identification of influential spreaders in complex networks[J].NAT PHYS,2010,6(10): 888-893.

[9] NEWMAN M.The structure and function of complex networks[J].Siam Review,2003,45(2):167-256.

[10]COSCIA M.A classication for community discovery methods in complex networks[J],Statistical Analysis,2011,4 (5) :512-546.

[11]赵之莹.基于网络社团结构的节点传播影响力分析[J].计算机学报,2014,37(4):753-766.

[12]BLONDEL V D.Fast unfolding of community hierarchies in large networks[J].Journal of Statistical Mechanics: Theory andexeriment,2008(10): 10008.

[13]HUA B.Identifying all-around nodes for spreading dynamics in complex networks [J].Physica ,2013,391(15):4012-4017.

[14]YOUSSEF M.Anindividual-based approach to SIR epidemics in contact networks[J].Journal of Theoretical Biology,2011,283(1):136-144.

中图分类号：TH-39;TP274+.5

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201607018

Fast Identifying Important Nodes in the Industrial Control System

Abstract：Industrial control system reliability,stability,survivability is a primary security issues of the industrial control system.In order to improve system security,the method of fast identifying important nodes in the industrial control systems is introduced.Depth integration of industrialization and informationization of large and complex industrial control systems,the evaluation important nodes method is proposed based on the complex network theory.In the view of the uneven and community distribution of industrial systems,and blending organically the degree centrality,the K-shell and the community diffusion,tactfully put forward ER+ methods and analysis the actual mining samples.The experimental results of SIR dynamics suggest that the ER+ method is more accurate,effective,stable.

Keywords:Industrial control systemER+SIRReliabilitySecurityIndustrializationInformatizationInformation safety

修改稿收到日期： 2015-05-29。

第一作者张醒(1989—)，男，现为华东理工大学控制科学与工程专业在读硕士研究生；主要从事工业控制系统、复杂网络方向的研究。