微陀螺仪检测控制系统设计与实现

王晓雷　赵向阳　刘玉翠　李宏生　张吉涛　曹玲芝

(郑州轻工业学院电气信息工程学院1，河南 郑州　450002；河南机电高等专科学校汽车工程系2，河南 新乡　453003；东南大学仪器科学与工程学院3，江苏 南京　210096)



微陀螺仪检测控制系统设计与实现

王晓雷1赵向阳2刘玉翠1李宏生3张吉涛1曹玲芝1

(郑州轻工业学院电气信息工程学院1，河南 郑州450002；河南机电高等专科学校汽车工程系2，河南 新乡453003；东南大学仪器科学与工程学院3，江苏 南京210096)

摘要：针对微陀螺仪开环检测的不足，在电容平衡梳齿微结构的基础上，提出了基于FPGA的微陀螺仪闭环检测控制方案。设计了电容电压变换及调理电路，得到了反映梳齿电容振动情况的电压信号。以FPGA为数字信号处理平台，设计了信号生成电路、自适应正交解调电路和校正电路，实现了对微陀螺仪信号的解调和处理。结合A/D和D/A变换，构建了微陀螺仪闭环检测系统。试验结果表明，在设计的闭环检测平衡回路控制下，微陀螺仪的标度因数线性度和对称性较开环检测时均有较大程度的提高，测量范围、阈值和分辨率等性能指标也得到了不同程度的改善。

关键词：微陀螺仪FPGAMEMS控制系统现场可编程门阵列平衡回路数字信号处理闭环检测模数转换

0引言

微陀螺仪是利用MEMS技术加工而成的角速度传感器。由于其具有体积小、质量轻、功耗小、成本低和易集成等特点，被广泛应用于飞行器姿态控制、地质勘探与大地测量、汽车安全行驶与导航等众多领域[1]。

由于没有高速旋转的转子，振动式微陀螺仪具有寿命长和稳定性高等[2]特点，是当前微陀螺仪发展的主流。微陀螺仪在驱动力的作用下沿驱动方向作受迫运动。根据哥氏效应，当垂直于驱动和检测模态的平面有角速度输入时，检测模态将产生振动，其振动幅值与输入角速度有关。驱动模态振动是检测模态测量的前提，通过测量检测模态的振动幅值，即可求得输入角速度。国内外关于驱动模态控制的研究很多，主要集中在驱动振动的频率控制[3]和幅度控制[4]，均已获得较好的控制效果；对于检测模态，通常采用开环检测[5]直接实现，而对闭环控制检测研究较少，目前还停留在理论研究阶段[6-7]。

闭环检测是一种间接检测方法，将哥氏振动幅值经校正补偿后作为控制量，作用在微结构上产生静电力平衡哥氏力，从而抑制哥氏振动。本文采用闭环控制技术，设计了一种基于FPGA的微陀螺仪检测模态控制电路，实现对哥氏振动幅值的间接求解。该方法原理简单、容易实现，同时对微陀螺仪的标度因数线性度、对称性等关键性能指标的改进具有积极意义。

1微陀螺仪振动闭环检测控制技术

1.1微陀螺仪原理

微陀螺仪是一种测量旋转角速度的惯性传感器，根据哥氏效应原理工作。以线振动梳齿电容式微陀螺仪为例，其原理如图1所示。x轴方向为驱动模态，当一定频率的外力作用在驱动梳齿时，微陀螺仪质量块沿x轴作机械振动，驱动检测梳齿可对振动情况进行监测和控制；当沿z轴有角速度输入时，质量块将产生沿y轴方向的哥氏振动，振动幅值与输入角速度有关，检测质量块的振动幅值可求解输入角速度。为了优化性能，通过一组检测平衡梳齿平衡哥氏力，抑制哥氏振动，实现对输入角速度的闭环检测。

图1　微陀螺仪原理示意图Fig.1　Schematic diagram of micro-gyroscope

1.2微陀螺仪闭环检测控制方案

微陀螺仪驱动模态的振动为检测模态提供动力基础，因此必须对其振动频率和振动幅值进行控制，常采用自激[8]或锁相环[9]方式保持振动频率跟踪谐振频率变化，以AGC方式[10]稳定振动幅值。检测模态主要由检测梳齿、电容电压转换、A/D转换、数字控制振荡器(digital controlled oscillator,DCO)、FPGA数字信号处理、D/A转换、信号放大和检测平衡梳齿振动等部分组成，如图2所示。

图2　微陀螺仪闭环检测电路框图Fig.2　Block diagram of the closed-loop detection circuit of micro-gyroscope

当有角速度输入时，微陀螺仪检测模态梳齿产生振动，带动梳齿电容变化，经电容电压转换和信号调理，得到表征梳齿振动的电压。为了能够灵活高效地处理信号，特使用FPGA数字处理器。通过正交解调和滤波求取哥氏振动幅值，以振幅校正结果作为控制量，调制到同频率振动信号上输出作用于检测平衡梳齿，以产生平衡反作用力，抑制哥氏振动。A/D转换芯片采用24位高精度转换器，D/A采用16位精度转换器。数字处理部分包含信号产生、解调、滤波、校正网络以及乘法电路等。

2检测闭环控制电路设计

按照图2所示的微陀螺仪闭环检测系统框架，设计检测模态闭环控制电路。前端微结构信号转换部分采用模拟电路实现，包括微陀螺仪检测模态接口电路、电容电压变换和调理电路；后端信号处理部分采用FPGA数字算法实现；模拟和数字电路之间由A/D和D/A转换电路相连接。

2.1前端模拟部分

微陀螺仪的检测模态信号是被载波调制过的高频信号，载波频率通常为2～10 MHz。电容电压转换电路不仅对高频信号进行一次解调，而且通过转换得到易于处理的电压信号。通常解调电路可采用环形二极管解调电路和双路积分解调电路[11]等。双路积分解调电路采用多个运算放大器形成积分和放大电路，结构复杂；而环形二极管解调电路采用四个参数完全一致的二极管构成环形电路，结构简单、精度高且易于实现，如图3所示。

图3　电容电压转换电路Fig.3　Capacitance-voltage converting circuit

图3中：载波为方波，幅值Uc；C1、C2为微陀螺仪差分检测电容，静态时电容值均为C0，变化量为ΔC；D1～D4为四个高频检波二极管，导通压降均为Ud；C3和C4为两个充放电电容，输出差分电压；差动运算放大器A，增益为Ka，输出单路转换电压U0，可采用精密仪表放大器。

根据充放电原理，可得到环形二极管解的表达式为：

(1)

可见，输出电压U0的大小与差分放大器增益Ka、载波幅值Uc成正比，与微陀螺仪的静态梳齿电容C0成反比。

2.2A/D和D/A转换

A/D和D/A转换器是模拟信号和数字信号之间的桥梁。A/D转换器对微陀螺仪检测信号进行采集；D/A转换器完成数字信号到模拟信号的转换，用于静电力驱动和哥氏力平衡。

A/D转换器采用ADI公司的24位高性能过采样逐次逼近型模数转换芯片AD776x。该芯片具有较宽的动态范围和输入带宽，总谐波失真为-118dB，功耗为15mW，温漂低，最高采样频率可达128kHz。AD776x为全差分输入，正负输入端信号范围均在0～Uref之间，且以Uref/2为中心上下波动。电路连接简单，主要通过CS、MCLK、SCLK、SDO和DRDY等信号，实现模拟信号采样。

D/A转换器采用TI公司的16位超低功耗电压输出数字模拟转换芯片DAC883x。该芯片功耗低，以3V供电时，功率仅为15μW；线性度好，准确性高，线性误差为1LSB；工作频率高，可达50MHz；具备快速SPI接口总线，连接方便；可实现双极性电压输出。

2.3数字部分

系统数字部分采用Altera公司的EP3C系列FPGA芯片，便于后续集成和移植。该芯片性价比高、片上资源丰富、逻辑单元和硬件乘法器多、存储空间大、运算速度快，可满足微陀螺仪信号处理的要求。

①DCO正交信号生成。

在数字化测量与控制中，采用数字算法进行信号处理。为实现数字解调，需要两路正交信号作为激励微陀螺仪振动的驱动信号，同时用于检测信号解调。常用的数字信号生成方法主要有查找表法、CORDIC方法、复数乘法等。查找表法采用预设的表格存储正余弦值。当精度较高时，要占用大量的存储空间。CORDIC方法通过坐标旋转一系列微小角度、逐次迭代计算产生正余弦三角函数，其精度取决于迭代次数；复数乘法[12]基于幅度相乘、相角相加的原理实现，无需大量迭代，方法简单、运算速度快。

假设复数a=ra(cosα+jsinα)，b=rb(cosβ+jsinβ)，则有：

ab=rarb[cos(α+β)+jsin(α+β)]

(2)

如果b固定，a和b的乘积作为下一次的乘数与b相乘，这样乘积的相角在单位圆中以β为增量旋转。相角增量决定向量旋转的角速度，最终决定生成的输出信号频率，可表示为：

(3)

式中:fclk为系统时钟频率。

采用复数乘法算法，按照一定的角度增量，存储2π范围内的值，通过查表可以生成一定频率范围内相互正交的正余弦函数。

②LMSD解调电路。

受到微机械加工工艺限制，微陀螺仪的驱动模态和检测模态存在一定的耦合。当有角速度输入时，在检测模态产生哥氏振动，同时还存在部分驱动模态耦合引起的正交振动，因此，检测模态的振动是哥氏运动和正交运动的合运动。哥氏运动来源于驱动振动速度，正交运动来源于振动位移，两者相互正交。为了求取哥氏振动位移，须进行正交解调。常用的解调方法有乘法解调和LMSD最小均方误差解调方法。乘法解调原理简单，但是会产生较大的二倍频信号；LMSD解调方法是一种自适应控制滤波器，使解调结果在均方误差最小意义上达到最优。

假设检测梳齿哥氏振动为xc=Accos(ωdk)，正交振动为xq=Aqsin(ωdk)，那么检测振动输出为：

x(k)=Accos(ωdk)+Aqsin(ωdk)

(4)

预测矩阵为W(k)=[Wc(k)Wq(k)]，则预测矩阵与单位矩阵R(k)=[cos(ωdk)sin(ωdk)]相乘，可得到一个估计信号，即y(k)=R(k)TW(k)，于是误差信号为:

e(k)=x(k)-y(k)

(5)

为了使误差e(k)在均方意义上最小，构造性能函数J(k) = E[e2(k)]，并对W(k)求梯度，得到最优预测矩阵为:

Wop(k)=R(k)-1x(k)

(6)

采用最速下降法寻找极值，得到预测矩阵的迭代公式为:

W(k+1)=W(k)+2μe(k)R(k)

(7)

式中:μ为收敛因子。试验证明，当μ=1/16时，收敛效果最优。

最小均方误差算法的迭代流程如图4所示。

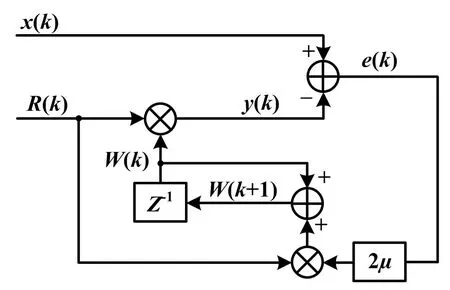
图4　最小均方误差解调算法流程图Fig.4　Flowchart of LMSD algorithm

③校正网络。

为了减小系统误差、提高系统开环增益、改善系统稳定性能，在系统中串联带有比例和积分环节的滞后网络G1(k)。然而，滞后网络的引入限制了系统的带宽。为了拓展带宽、提高系统的动态性能，必须串联超前网络G2(k)，因此G1(k)和G2(k)串联构成了滞后超前校正网络，即：

(8)

式中:Kp为增益;T1、T2、T3、T4为校正参数，其大小为T2>T1>T3>T4。通过调整校正参数，使闭环系统既能满足稳态性能，又可兼顾动态性能，以实现较好的控制效果。

3试验及分析

根据提出的检测方案，设计电路并制作PCB板，将真空封装的线振动MEMS微陀螺仪安装在PCB板上，调试至最佳状态。分别在开环和闭环下对标度因数、测量范围、阈值和分辨率等指标进行测试，具体测试数据如表1所示。由表1可见，与直接开环检测相比，采用闭环检测控制方案的微陀螺仪，哥氏力被控制力所平衡，质量块在y轴方向的哥氏振动被抑制，仅在平衡位置附近作微小振动，从而有利于抑制外界干扰；标度因数线性度和对称性分别提高5倍和13倍，测量范围、阈值和分辨率等指标均有不同程度的改善。

表1　性能指标比较Tab.1　Comparison of part of the performance indexes

4结束语

基于微陀螺仪电容梳齿微结构，提出了抑制哥氏振动的闭环检测方案；设计了闭环检测平衡电路，包括模拟部分、A/D和D/A转换器、数字部分。电容检测电路采用环形二极管电路进行电容电压转换和信号放大调理；数据转换采用高精度的A/D转换器和D/A转换器实现；数字处理采用FPGA数字处理器进行信号生成、信号解调、滤波、校正和闭环控制，提高了控制

系统的稳定性和动态性能。试验表明，微陀螺仪采用该闭环检测方案，可明显提高标度因数的线性度和对称性，并有效改善测量范围、阈值和分辨率等性能指标，进一步验证了该检测方案的有效性。

参考文献：

[1] 顾睿风,苏岩,朱欣华.微型惯性测量组合数据采集系统[J].自动化仪表,2011,32(2): 69-73.

[2] 王寿荣,黄丽斌,杨波.微惯性仪表与微系统[M].北京: 兵器工业出版社,2011.

[3]TATARE,MUKHERJEET,FEDDERGK.On-chipcharacterizationofstresseffectsongyroscopezerorateoutputandscalefactor[C]// 28thIEEEInternationalConferenceonMicroElectroMechanicalSystems(MEMS),2015: 813-816.

[4] 谭晓昀,雷龙刚,王冠石.电容式微机械陀螺双环路闭环驱动电路研究[J].传感技术学报,2010,23(10): 1449-1453.

[5] 贾方秀,裘安萍,施芹,等.硅微振动陀螺仪设计与性能测试[J].光学精密工程,2013,21(5): 1272-1281.

[6]SUNGS,YUNS,SUNGWT,etal.Anovelcontrolloopdesignanditsapplicationtotheforcebalanceofvibratoryratesensor[J].InternationalJournalofControl,AutomationandSystems,2009,7(4): 545-552.

[7]CUIJ,GUOZ,ZHAOQ,etal.Forcerebalancecontrollersynthesisforamicromachinedvibratorygyroscopebasedonsensitivitymarginspecifications[J].JournalofMicroelectromechanicalSystems,2011,20(6): 1382-1394.

[8] 王存超,苏岩,王寿荣.硅微振动陀螺仪驱动器自激驱动研究[J].传感技术学报,2006,19(2): 364-366.

[9] 王晓雷,张印强,杨成,等.基于数字锁相环控制的硅微陀螺仪驱动模态分析与实验[J].东南大学学报：自然科学版,2013,43(4):747-752.

[10]CHENF,YUANW,CHANGH,etal.Designandimplementationofanoptimizeddoubleclosed-loopcontrolsystemforMEMSvibratorygyroscope[J].IEEESensorsJournal,2014,14(1): 184-196.

[11]高雅彪,毛伟玲,李醒飞.石英挠性摆式加速度计闭环检测电路设计[J].电子技术应用,2012,38(2): 70-72.

[12]PALOMAKIK,NIITTYLAHTIJ,RENFORSM.Numericalsineandcosinesynthesisusingacomplexmultiplier[C]//IEEEInternationalSymposiumonCircuitsandSystems,1999: 356-359.

中图分类号：TH-3;TP271

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201607013

DesignandRealizationoftheDetectionandControlSystemforMicro-gyroscope

Abstract：Aiming at the deficiency of open-loop detection for micro-gyroscope,on the basis of the micro-structure of capacitance balance comb teeth,the closed-loop detection and control scheme based on FPGA is put forward.The capacitance/voltage transformation and conditioning circuit are designed,and the voltage signal reflecting the capacitance vibration of comb teeth is acquired.With the FPGA as the digital signal processing platform,the signal generating circuit,adaptive orthogonal demodulation circuit and correction circuit are designed,and the demodulation and processing of the signals of micro-gyroscope are implemented. Combining with A/D and D/A conversion,the closed loop detection system of micro gyroscope is constructed.The experimental results show that under the control of closed loop detection balance loop,the linearity and symmetry of the scale factors of micro gyroscope are better than those of open loop detection.The performance indexes,including measurement range,threshold and resolution have been improved at some extent.

Keywords:Micro-gyroscopeFPGAMicro-electromechanical systemsControl systemField programmable gate arrayBalance loopDigital signal processingClosed-loop detectionAnalog digital conversion

郑州轻工业学院博士科研基金资助项目(编号：2014BSJJ046)。

修改稿收到日期：2016-01-07。

第一作者王晓雷(1980—)，男，2014年毕业于东南大学仪器科学与技术专业，获博士学位，讲师；主要从事传感器技术与测控系统方向的研究。