投影与视图常见错误分析

文/汪国刚



投影与视图常见错误分析

文/汪国刚

责任编辑：王二喜

投影与视图是图形变化中的新内容，在中考中多以选择题、填空题的形式出现，偶尔以解答题的形式出现.现以2015年中考题为例，把常见的错误剖析如下，供你学习时参考.

一、平面展开图与立体图的互换

例1（2015年广安卷）在市委、市政府的领导下，全市人民齐心协力，将广安成功创建“全国文明城市”，为此，小红特制了一个正方体玩具，其展开图如图1所示，原正方体中与“文”字相对面上标的字应是（）.

A.全B.明C.城D.国

错解：A或B或D.

错因分析：没有掌握立体图形与展开图的转化关系.在展开图中，相对面之间没有公共点，有交点的两个面一定相邻.

正解：选C.

例2（2015年无锡卷）如图2的正方体盒子的外表面上画有3条粗黑线，将这个正方体盒子的表面展开（外表面朝上），展开图可能是（）.

图1

图2

错解：A或B或C.

错因分析：从立体图形可以知道，有黑线的面与无黑线的面是相对面，因此选项A错误；将展开图折叠，三条黑线段要构成一个封闭图形，这样可以排除B、C.

正解：利用排除法或动手操作，即可得到正确答案.选D.

温馨小提示：正方体的展开图，从相对面没有公共点入手，分析面与面之间的关系，或模拟图形进行操作，可以避免错误，从而迅速解题.

二、确定几何体三视图时，观察方向或理解题意出错

例3（2015年河南卷）如图3所示的几何体的俯视图是（）.

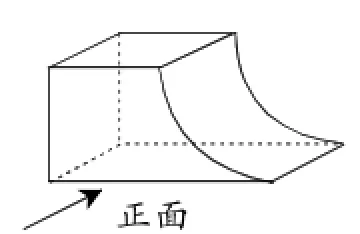
图3

错解：A或D.

错因分析：混淆视图概念，联想平面图形出错.

正解：从上往下观察几何体，得到的平面图形为选项B.选B.

例4（2015年张家界卷）下列立体图形中，它们各自的三视图有两个相同，而另一个不相同的是（）.

A.①②B.②③C.②④D.③④

错解：A或B或C.

错因分析：没有认真审题而出错.

正解：选D.

温馨小提示：要熟悉常见几何体（如球、正方体、长方体、圆柱体、圆锥等）的三视图，了解它们的区别与联系.

三、漏画轮廓线，混淆虚线与实线的区别

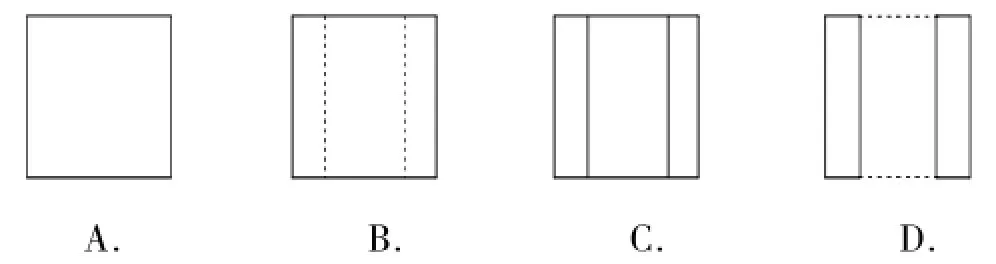
例5（2015年贵阳卷）如图4，一个空心圆柱体，其左视图正确的是（）.

错解：A或C或D.

错因分析：选A，忽略圆柱体空心部分用虚线表示；选C，看不到的轮廓线要用虚线表示；选D，观察几何体出现错误.

正解：画视图时，看得见的轮廓线画成实线，看不见的画成虚线,因为中间有两条看不见的线，所以有两条虚线.选B.

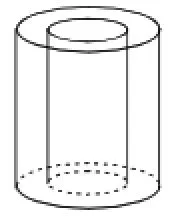
图4

温馨小提示：在画三视图时，要注意实线和虚线的区别.

四、由三视图判断几何体

例6（2015年日照卷）小红在观察一些小立方块搭成的几何体时，发现它的主视图、俯视图、左视图均如图5，则构成几何体的小立方块的个数有（）.

A.3个B.4个C.5个D.6个

错解：A或D.

错因分析：选A，认为组合体的三视图都一样，就是三个小立方块搭成；选D，误认为从三个不同方向观察都一样，于是小立方块的个数有3×2＝6个.

正解：解法一：从俯视图发现有3个小立方块，从左视图发现第二层最多有1个小立方块，则构成该几何体的小立方块有4个.选B.

解法二：如图6，在俯视图上标记数字，主视图有2列，每列正方形的个数分别为2和1，在俯视图中，第1列两个正方形都标上2，第2列的正方形标上1.左视图有2列，每列正方形的个数分别为2和1，在俯视图第一行的正方形上标上2，第二行的正方形上标上1.最后，按“就小不就大”取数，小立方块的个数有2+1+1＝4（个）.选B.

例7（2015年怀化卷）如图7，甲、乙、丙图形都是由大小相同的小正方体搭成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是（）.

A．仅有甲和乙相同

B．仅有甲和丙相同

C．仅有乙和丙相同

D．甲、乙、丙都相同

错解：D.

错因分析：只看到俯视图中小正方体的个数和相等，没有考虑位置不同.

正解：甲的主视图有2列，每列小正方形数分别是2、2；乙的主视图有2列，每列小正方形数分别是2、1；丙的主视图有2列，每列小正方形数分别是2、2.主视图相同的是甲、丙.选B.

图5

图6

图7

温馨小提示：主视图的列数与俯视图的列数相同，且每列小正方形数为俯视图该列小正方形的最大数；左视图的列数与俯视图的行数相同，且每列小正方形数为俯视图相应行正方形的最大数.

五、利用三视图进行计算，忽略“长对正，高平齐，宽相等”致错

例8（2015年呼和浩特卷）图8是某几何体的三视图，根据所标的数据求得该几何体的体积为（）.

A.236πB.136π

C.132πD.120π

错解：A或C或D.

错因分析：没有理解几何体的形状和数据的对立关系，导致计算错误.

正解：由三视图可知，该几何体由两个圆柱体组成.

其体积为：π×22×2+π×42×8＝8π+128π＝136π.选B.

温馨小提示：由三视图还原几何体时，要有想象力，根据三视图计算几何体的体积或表面积时，需要把主视图、左视图、俯视图一同联系起来确定几何体形状，明确数据的对应关系，从而根据公式求体积或表面积.

图8

六、混淆平行投影与中心投影性质致错

例9在同一时刻的阳光下，小明的影子比小强的影子长，那么在同一路灯下（）.

A．小明的影子比小强的影子长B．小明的影子比小强的影子短

C．小明的影子和小强的影子一样长D．无法判断谁的影子长

错解：A.

错因分析：中心投影与平行投影不同，中心投影中物体的影长与物体到光源的远近、高低有关，平行投影中物长与影长成正比例关系.

正解：在同一时刻的阳光下，小明的影子比小强的影子长，则小明比小强高，但在同一路灯下，离路灯的远近不同，则影子长短不同，故无法判断谁的影子长.选D.

温馨小提示：在平行投影中，物与影对应点的连线是平行的，因此物高与影长成比例；在中心投影中，物与影对应点的连线交与一点，因此物体与光源的远近、高低不同，物体的影长就不同.