在体验中探寻 在尝试中思考——有关“一笔画”的教学设计

汪松浩

在体验中探寻在尝试中思考
——有关“一笔画”的教学设计

汪松浩

“一笔画”这个经典的数学素材源于数学家欧拉提出的“七桥问题”。从数学教学素材的开发角度来看，“一笔画”一直是小学数学课堂中用以引导孩子发现规律的上佳素材。常见的课堂探索方法是，引导孩子研究一定数量的图形，并对其中的奇点与偶点个数进行观察与统计，通过列表发现一笔画的规律：奇点个数是0或2时，这个图形是能够一笔画的。然后就是对这个规律的运用，对各种难度的图形能否一笔画进行判断甚至尝试画出。这一类设计无疑是参考了欧拉研究该问题时的数学方法，但是很难回答这样几个问题：

1.孩子是如何将研究的对象自主确定到奇点、偶点上的？

2.获取一笔画蕴含的数学规律之后，用于进行判断或绘画，对思维训练究竟有多大的意义？

3.规律虽然找到，为何这么奇怪偏偏是“0”或“2”个奇点数？背后的数理是什么？

由此看来，这一类设计虽然精彩，但显然对训练孩子的数学思维在若干细节上尚未得到落实，孩子在训练过程中的探索还算不上是真探索。训练素材要落实其训练意义，必须是从孩子的原生认识出发，选择适合孩子的认知方式，通过一个重过程、轻结果的探索过程来实现。正是基于以上考量，笔者将“一笔画”引入了小学二年级的课堂，通过低学段孩子在课堂中的表现，反思利用这类素材训练学生思维究竟该如何细化，才能真正发挥出其应有的作用，使思维训练落到实处。

【教学过程】

一、“一笔画”初步认知

教师徒手在黑板上画了一幅“一笔画”图案（图1），然后提问：你看到了什么？你们发现这幅图的画法有什么特别之处吗？你知道“一笔画”有什么要求吗？

学生回答后，教师让学生自由创作，初次体验一笔画。教师收集部分优秀作品进行展示、点评。

接着教师出示图2，让学生尝试一笔画。学生尝试之后，发现这个图形不能一笔画。教师提问：究竟什么样的图形能一笔画？（板书课题：一笔画）

图1

图2

设计意图：教者以画开课，以“绘”相承，意在调动学生的学习兴趣及参与热情。在此基础上出示图2，让学生从动手绘图的体验转向数学规律的探索，进而明确本堂课的学习目标。

二、“一笔画”规律探索

1.体验像一根绳子一样的一笔画

教师手绘一组图形（如图3所示）。

图3

学生一眼看出能一笔画，还说出：不但能画，而且都有两种画法，不仅可以从这端画到那一端，也可以从那端画到这一端。

教师要求学生讨论两个问题：

（1）这样的简单图形一笔能画是显而易见的，那图形能不能一笔画一定与什么无关？

教师通过将线条画得更长或擦掉一小节，或是将一部分改画得歪斜一点，并在展示台放大（缩小）图形，让孩子体会这些变化都不会改变这个图形关于一笔画的相关性质。（板书：有关，无关）

（2）手拿学生的鞋带，提问：借助这根鞋带，你能解释这些图形都有两种画法背后的理由吗？

引导孩子用绳子类比一笔画，一根绳子有两个绳头，所以有两种画法。或者说无论怎么画都必须以某个绳头为起点，不能从绳子的中间画起。（板书：绳头）

设计意图：通过具体的图形或实物，帮助学生在体验中思考，体会在对规律的探索中什么是相关因素，什么是无关因素。尤其是借用鞋带帮助孩子理解一笔画，给了学生思维的“拐杖”。

2.寻找绳头

教师手绘第二组图形（如图4所示），提问：孩子们，你们能找到这一组图形的绳头，并且成功地将它们一笔画成吗？

图4

学生进行尝试与体验。接着教师让学生挑战第三组图形（如图5所示），提问：孩子们，你们觉得一笔画能否成功，最关键的是什么？（板书：关键，寻找绳头）

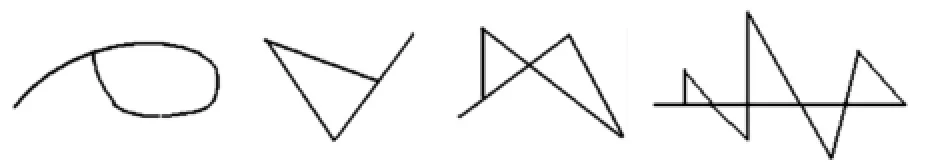
图5

3.什么样的点才是绳头呢？

教师提出体验要求：孩子们，我们已经找到了画一笔画的关键是寻找绳头。现在老师画一个一笔画图形，请仔细观察绳子不断变长的时候，绳头所在的点会有什么变化。

教师演示（如图6所示）。

图6

学生讨论并回答：绳头在三岔路口，其他点是十字路口或者拐弯路口。

教师追问：绳头一定是在三岔路口吗？还有别的情形吗？

教师在原图上继续画（如图7所示），带孩子体会“奇点”与“偶点”之间的转化。

图7

引导孩子体会点周围相连的线条数量，由“三岔路口”提升认识到“单岔路口”，再总结到“单点”。（板书：单点）

教师继续追问：绳头有可能藏起来吗？这个时候又是什么情形呢？

教师将刚才的图形完成首尾相连的状态（如图8所示），让孩子在体验中提升认识：能一笔画的图形有一类是能找到2个单点，还有一类是没有单点。

图8

教师再次拿出鞋带做道具，提问：你们知道绳头哪去了吗？你能用鞋带说明吗？

带孩子体验两个绳头相接的情况，体会单点是如何消失的，以及在这种情况下的起点和终点，即从任意一个点开始都可以一笔画成。

设计意图：继续借助有梯度的画图体验，让孩子在画图的过程中体会什么是关键因素，关键因素具有什么特征，在不断升级的体验中，提升对问题的认识，形成准确的概念。

三、“一笔画”游戏大挑战

教师展示网络游戏“一笔画”，请孩子上台挑战。学生相继上台挑战“一笔画”。

四、课堂小结及作业

教师引导学生回顾这节课所学的内容，然后布置作业：请你画一个有而且只有3个单点的图形。如果你认为不能画出，请说出理由。如果你认为能画出，请提供画好的图形。

设计意图：作业的设计意图是引导学生从另一个角度反思刚才研究的问题，达到对新知的更深刻、全面的认识。孩子对数理关系的理解是有孩子的视角和方式的，必须要尊重这种状态，才能领着孩子进入到数学的花园，体会到数学的美与趣味。

（作者单位：湖南一师一附小）

点评：“一笔画”是一个叫图论的数学分支中的问题。图论以图为研究对象。当然，由数学的抽象性不难知道，这里的图不是通常意义上（比如美术、工程等）的图，而是一个抽象的数学结构。图中有两种对象，一个叫点，代表事物，一个叫边，代表事物之间的联系。这个数学分支起源于一个类似游戏的问题，即哥尼斯堡七桥问题：一个散步者怎样才能够一次不重复地走遍如图9所示的七座桥？这个问题可以抽象成能否一笔画成如图10所示的图形，即所谓一笔画问题。欧拉漂亮而彻底地解决了这个问题。

图9

图10

欧拉的结论是：一个图（严格地说，应该说一个连通图）能一笔画成的充分必要条件是：这个图有0个或2个奇点。结论如此简洁，以至于问题的各种复杂性立刻烟消云散，一个图能否一笔画成几乎是显而易见的。

拿一笔画来教学，通常有两个价值追求：一是培养学生的抽象能力，主要关注从“能否不重复地走完七座桥”到“能否一笔画一个图”的转化；二是培养学生归纳概括的能力，主要关注如何得出一个连通图能否一笔画成的判断方法。

汪老师的课另辟蹊径，创造性地提出了“一根绳子一样的一笔画”，“寻找绳头”。这种思路的重要价值在于，它解决了一个问题：如何将能否一笔画的问题与图中点上的连线的奇偶性联系起来。事实上，这个问题的解决是非常困难的。天才如欧拉才有可能把这两个看起来无关的问题联系起来。这个问题也是很重要的，尤其是对于低年级的孩子而言。因为他们基本无法体会将“能否不重复地走完七座桥”抽象成“能否一笔画一个图”的过程及其意义，也难以完成对一笔画充要条件的归纳。若不解决这个问题，剩下能做的就只有教结论然后巩固结论了，而这里的结论本身恰恰是很简单且教育价值有限的。

“一根绳子一样的一笔画”“寻找绳头”，这些是很高明的处理手段。对低年级的学生而言，点、线、奇、偶之类稍显抽象，难以调动他们已有的经验，而绳子、绳头及其个数则直观，也与他们的某些生活经验相关。另外，若细想一下，一个图能否一笔画，不就是看它能否拉直成一根绳子吗？如何拉直呢？不就是寻找绳头（即确定从哪下手）吗？

这种手段其实也暗合了欧拉最原始的思考方式。欧拉在1736年提交给彼得堡科学院一篇题为“问题解决与位置几何”的论文（汉译可见姜伯驹先生《一笔画和邮递路线问题》一书），就是解决七桥问题的。在欧拉的论文中并没有画出我们通常见到的图10，而是画出了下面的图（图11、图12）。在这两幅图中，我们不难发现绳子的影子。

图11

图12

（长沙市教育科学研究院张新春）