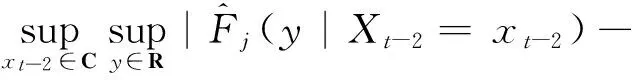二阶部分线性自回归模型的稳健估计
刘常胜,宋红伟
(1. 河南城建学院数理系,中国 平顶山 467044;2. 河南科技大学数学与统计学院,中国 洛阳 471023)
二阶部分线性自回归模型的稳健估计
刘常胜1,宋红伟2
(1. 河南城建学院数理系,中国 平顶山467044;2. 河南科技大学数学与统计学院,中国 洛阳471023)
本文将稳健估计程序思想运用到二阶部分线性自回归模型中, 得到了未知参数β和非参数函数g(·)的稳健估计. 在一定的条件下, 证明了未知参数和非参数函数估计的相合性. 并通过时间序列的数据模拟验证相合性结果.
自回归模型;相合性;稳健估计
对于部分线性模型,Bianco[1]运用一定的稳健估计程序, 得到了该模型参数和非参数函数的稳健估计. Tong[2]提到, 一些非线性时间序列模型不能通过线性进行拟合, 因此必须通过非线性方法来处理. 但是在某些情况下, 完全的非线性自回归函数失去了序列前后期关系的重要信息, 比如忽略了前后期之间存在的线性依赖关系. 拟合非线性时间序列之间关系的一个合理方法是使用部分线性自回归模型.

(1)
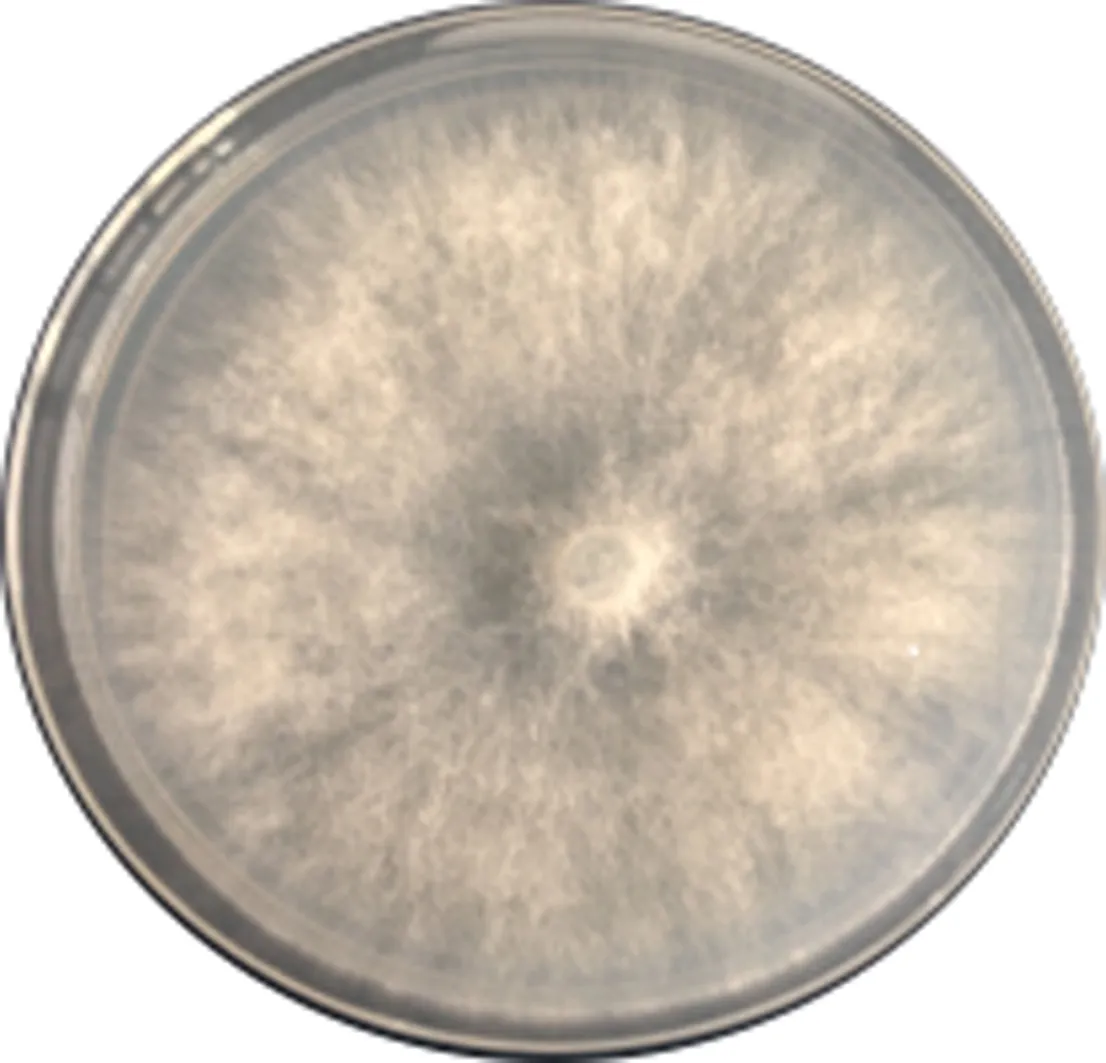
这里t>max(cp,dq), 1≤c1 下述模型是模型(1) 的简化模型, 它是二阶部分线性自回归模型. Xt=βXt-1+g(Xt-2)+et,3≤t≤T, (2) 关于模型(1)和(2),Robinson[3]首次引入并展开讨论, Chen等人[4]用光滑样条方法估计非参数函数, 获得最小二乘估计,Gao和Liang[5]利用权函数方法确立了参数β的最小二乘估计的渐进正态性, Gao[6]和Liang[7]确立了该最小二乘估计的其他一些重要结论. 部分线性自回归模型是部分线性模型与自回归模型的有机结合, 文献[8-11] 将部分线性模型讨论引向深入. 文献[12] 讨论了分歧泊松自回归模型的马尔可夫性. 众所周知, 线性模型和非线性模型极容易受异常值的影响, 部分线性模型也存在同样的问题. 本文的目的是针对二阶部分线性时间序列模型(2), 提出一个类似于文献[1] 的稳健估计方法, 得出一个稳健估计, 并研究该估计的相合性. 通过蒙特卡洛方法, 在正常数据和异常数据两种情况下, 对该稳健估计与经典的最小二乘估计进行比较. 1.1传统的最小二乘估计方法 对于二阶部分线性时间序列模型(2), 通过下列程序进行, 首先 g(Xt-2)=E{(Xt-βXt-1)|Xt-2}=E(Xt|Xt-2)-βE(Xt-1|Xt-2)=φ2(Xt-2)-βφ1(Xt-2). 自然,φi(i=1, 2) 和g的估计通常被定义为: (3) 这里Kh(·)=h-1K(·/h),K:R→R是一个核函数. (4) 1.2稳健估计方法的提出 对于二阶部分线性时间序列模型(2), 可以按照下面的步骤获得稳健估计: (5) (6) 第三步:定义非参数分量g(·) 为 1.3相合性 为了推导一些稳健估计相合性的结论,需要构造以下条件. A1. ψ:R→R是一个奇函数, 同时又是严格增、有界且具有连续的导数, 满足uψ′(u) ≤ψ(u). A2.F1(u|Xt-2=xt-2) 和F2(v|Xt-2=xt-2) 分别关于φ1(xt-2) 和φ2(xt-2) 是对称的. A4.F1(u|Xt-2=xt-2) 和F2(v|Xt-2=xt-2) 都是xt-2的连续函数,而且对任意紧集C⊂R,它们满足下面的等度连续条件:∀ε>0,∃δ>0:|ω1-ω2|<δ, 满足 A5. 核函数K:R→R 是有界的非负函数,满足∫K(u)du=1,∫ |u|K(u)du<∞, |u|K(u)→0(u→∞) 和一阶Lipschitz条件. A6. 序列h=hT满足当T→∞ 时,hT→0,ThT→∞ 和ThT/logT→∞. 假定条件A1~A6可以分成三类,第一类确立了得分函数ψ满足的标准条件;第二类阐述了Xt-2的密度函数及条件分布F1(u|Xt-2=xt-2) 和F2(v|Xt-2=xt-2) 所满足的正则条件,这意味着,对任意紧集C,0 本文主要得到以下两个定理,即参数β和非参数函数g(·) 的稳健估计的相合性. 定理1设(xt,xt-1,xt-2)′, 3 ≤t≤T满足二阶部分线性自回归模型(2), 记P为(r2,t,r1,t)′=(xt.-φ2(xt-2),xt-1-φ1(xt-2))′ 的概率分布. 令β(H) 为模型v=βu+ε的回归函数, 这里(v,u)′ ~H,ε和u相互独立,假定β(H) 在P处连续. 误差ε1, ε2,…, εT相互独立,均服从N(0, 1), 这种情形相当于数据没有异常值. 表1 β 的LS估计的相合性 表2 g(·) 的LS估计的相合性 表3 β的中位数估计med 的相合性 表4 g(·) 的中位数估计的相合性 通过以上4个表的数据,可以看出传统的最小二乘估计方法与稳健估计方法得到的数据拟合吻合程度都比较好,本文提出的稳健方法适用于时间序列的建模、估计和预测,为进行统计推断提出了一个新的方法. 为了得到本文的主要结果, 需要引入以下两个引理. 引理1假定条件A3~A6成立, 那么对任意紧集C⊂R, (1) 在条件A1~A2下,有 (7) (2) 如果F1(u|Xt-2=xt-2) 和F2(v|Xt-2=xt-2) 分别有唯一的中位数φ1(xt-2) 和φ2(xt-2),有 (8) 证(1) 根据Boente 和Fraiman[13]的定理3.3 可以证明此结论. (2) 假定条件A4的等度连续条件和条件中位数的唯一性, 蕴含着φj(xt-2) 是一个连续函数, 因而对任何固定的a∈R, 函数ha(t)=Fj(a+φj(xt-2)|Xt-2=xt-2) 也是t的连续函数. 对任给的ε>0,∃0<δ<ε, 使得 (9) 则根据条件中位数的唯一性及式(9). 对j=1,2, (10) (11) (12) (1) 对任何有界连续函数f:R2→R, 有 |EQT(f)-EPT(f)|→a.s.0; (13) (2)Π(QT,P)→a.s.0, 其中Π为Prohorov距离. 从式(11) 和强大数定律,则存在N⊂Ω, 使得P(N)=0, 那么对任何ω∈Nc, 有 (14) (15) (3) 从以上证明自然得到此结论. 定理1的证明: 定理2的证明:由定理1和引理1知 [1]BIANCO A, BOENTE G. Robust estimators in semiparametric partly linear regression models[J]. J Stat Plan and Infer, 2004,122(1):229-252. [2]TONG H. Nonlinear time series: a dynamical system approach[M]. Oxford: Oxford University Press, 1990. [3]ROBINSON P M. Root-N-consistent semiparametric regression[J]. Econometrica, 1988,56(4):931-954. [4]CHEN H, CHEN K W. Selection of the splined variables and convergence rates in a partial spline model[J]. Can J Stat, 1991,19(3):323-339. [5]GAO J, LIANG H. Asymptotic normality of pseudo-LS estimator for partly linear autoregression models[J]. Stat Probab Lett, 1995,23(1):27-34. [6]GAO J. Semiparametric regression smoothing of non-linear time series[J]. Scand J Stat, 1998,25(3):521-539. [7]LIANG H. Asymptotically efficient estimators in a partly linear autoregressive model[J]. Syst Sci Math Sci, 1996,9(2):164-170. [8]BIANCO A, BOENTE G, MARTINEZ E. Robust tests in semiparametric partly linear models[J].Scand J Stat, 2006,33(3):435-450. [9]BIANCO A, BOENTE G. On the asymptotic behavior of one-step estimates in heteroscedastic regression models[J]. Stat Probab Lett, 2002,60(1):33-47. [10]洪圣岩. 一类半参数回归模型的估计理论[J]. 中国科学:A 辑, 1991,34(12):1258-1272. [11]HONG S Y, CHENG P. Bootstrap approximation of estimation for parametric in a semiparametric regression model[J]. Sci China Ser:A, 1993,36(3):239-251. [12]孙耀东. 分歧泊松自回归模型的马尔可夫性[J]. 湖南师范大学自然科学学报, 2011,34(4):18-20. [13]BOENTE G, FRAIMAN R. Strong uniform convergence rates for some robust equivariant nonparametric regression estimates for mixing processes[J]. Int Stat Rev,1991,59(3):355-372. (编辑HWJ) 重要启事 “优先数字出版”是以纸质版期刊录用稿件为出版内容,先于纸质期刊出版日期出版的数字期刊出版方式.我刊已于2012年起与中国学术期刊(光盘版)电子杂志社签订了优先数字出版协议.凡被我刊录用的稿件一经优先数字出版,读者即可在中国知网(CNKI)全文数据库进行检索和下载.凡向本刊投稿的作者,如无特别申明,均被视为作者授权本刊编辑部在纸质期刊出版前,可以在中国学术期刊(光盘版)电子杂志社主办的“中国知网”(www.cnki.net)上优先数字出版;也被视为作者同意并授权我刊与其他电子杂志社签订的协议,并许可其在全球范围内使用该文的信息网络传播权、数字化复制权、数字化汇编权、发行权及翻译权,并不再额外支付稿酬. 本刊编辑部 Robust Estimation of Two Order Partially Linear Autoregressive Model LIUChang-sheng1,SONGHong-wei2* (1.Department of Mathematics and Physics, He’nan University of Urban Construction, Pingdingshan 467044, China;2.School of Mathematics and Statistics, He’nan University of Science and Technology, Luoyang 471023, China) In this paper, by applying the robust estimation procedure to two order partially linear autoregressive model, the robust estimators of unknown parametericβand nonparametric functiong(·) were obtained. And the consistency of unknown parametric and nonparametric function estimators under certain conditions was confirmed. Time series simulation was employed to verify the consistency results. autoregressive model; consistency; robust estimation 图1 ZWC5菌株在PDA平板上的菌落形态(P.19)Fig.1 Colony morphology of fungus ZWC5 on the PDA culture medium(P.19) 图2 ZWC5-Pe对HepG2及SMMC-7721细胞形态的影响(P.20)Fig.2 Effects of ZWC5-Pe on cell morphology of HepG2 and SMMC-7721(P.20) 10.7612/j.issn.1000-2537.2016.04.015 2015-05-07 河南省科技计划项目支持(112300410191) ,E-mail:csliu@hncj.edu.cn O211.61, O212.1 A 1000-2537(2016)04-0089-06
1 稳健估计方法与主要结果







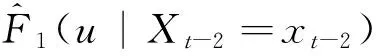


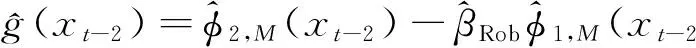







2 蒙特卡洛模拟
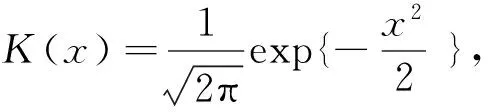
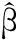



3 定理的证明