(p,q)型权投射线的凝聚层范畴上的倾斜丛

陈金晶,林玉娜

(厦门大学数学科学学院, 福建厦门361005)



(p,q)型权投射线的凝聚层范畴上的倾斜丛

陈金晶*,林玉娜

(厦门大学数学科学学院, 福建厦门361005)

摘要：考察(p,q)型权投射线的凝聚层范畴上的倾斜丛,证明了其上的canonical倾斜丛总是构成一个slice,进而详细刻画了(p,q)型权投射线的向量丛子范畴的结构;进一步从不可分解对象,slice,level,domain等方面,阐述向量丛之间的一些重要性质,完全分类了所有的倾斜丛,即倾斜丛与向量丛范畴的slice一一对应.

关键词：权投射线；倾斜丛；slice

权投射线的概念是由Geigle等[1]引入的, 他们引入权投射线的初衷是为了给出代数表示论中的 canonical 代数在几何上的实现. 简单地说, 一条权投射线可以看成是在射影曲线P1(k)上两两不同的点λ1,λ2,…,λt赋予权p1,p2,…,pt得到的. 同时, 倾斜对象在范畴中起到了举足轻重的作用, Geigle等[1]进一步证明了权投射线的凝聚层范畴上总是存在着 canonical 倾斜层. Chen等[2]研究了权型为 (2, 2,n)的权投射线上凝聚层范畴的倾斜丛, 本研究主要利用 slice 完全刻画 (p,q)型权投射线上的所有倾斜丛.

1预备知识

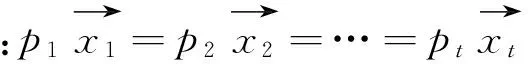
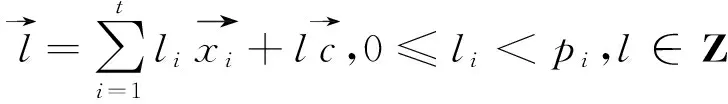
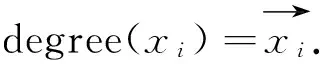
(s1,s2,…,st)(x1,x2,…,xt)=

(s1x1,s2x2,…,stxt)，

则F(p,λ)在G(p)作用下是稳定的.称F(p,λ)/G(p)是权型为P的权投射线,记为X.

X上的凝聚层范畴记为coh(X),这是一个Krull-Schmidt、态射有限、遗传的Abel范畴.coh(X) 中存在Serre对偶, 即给定任意的 F,G∈coh(X),存在如下同构映射

DExt1(F,G)→Hom(G,τF),

2(p,q)型权投射线凝聚层范畴上的倾斜丛

Geigle等[1]给出了权投射线的凝聚层范畴上的倾斜层的定义. 设T∈coh(X), 称 T 是一个倾斜层, 如果满足以下3条:

(i)Ext1(T,T)=0;

(ii) T生成Db(coh(X));

(iii)End(T)存在有限总体维数.

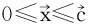
不失一般性,下面假设X是任意一条权型为(p,q)的权投射线.

对于任意范畴的Auslander-Reiten箭图,文献[4]给出了其上slice的定义. 特别地, 在vect(X)中给定任意的线丛X,存在从X出发以及到达X的两个slice,把它们分别记为S(X→) 和 S(→X).这两个slice具有如下的表达式:

S(X→)={F是线丛|Hom(X,F)≠0且

Hom(X,τiF)=0,任意的i∈N+};

S(→X)={F是线丛|Hom(F,X)≠0且

Hom(τ-iF,X)=0,任意的i∈N+}.

注意到给定两个线丛, 如果它们之间有非零态射, 那么有如下重要的观察.

引理1给定F, G 是任意的两个线丛. 若Hom(F,G)≠0, 则对于任意的n∈N,有

Hom(F,τ-nG)=Hom(τnF,G)≠0.

证明事实上, 对于任意的线丛 G,

因此,对于任意的线丛X,S(X→) 和S(→X) 的表达式可以简化为:

S(X→)={F是线丛|Hom(X,F)≠0且

Hom(X,τF)=0};

S(→X)={F是线丛|Hom(F,X)≠0且

Hom(τ-1F,X)=0}.

当权投射线X的权型为(p,q)时,知道其上的向量丛范畴vect(X)的不可分解对象均是线丛,通过观察发现canonical倾斜丛有如下性质．

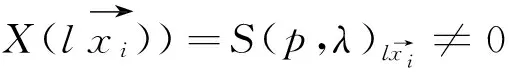
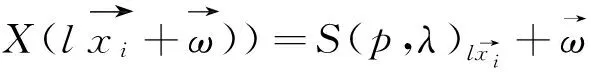
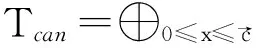
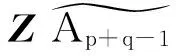
下面引入level及Domain的概念来得出主结论.

定义1给定任意的线丛F, 如下定义F的level, 记为 l(F):

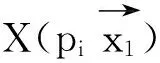
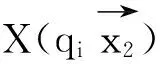
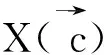
定义2给定任意的线丛F,称由F确定的Domain为

Dom(F)={G是线丛|存在m,n∈N使得τmG

∈S(→F),τ-nG∈S(F→)}.

为了找出凝聚层范畴coh(X)上的倾斜层,下面给出一个线丛之间无非零扩张的充要条件:

引理3给定任意的线丛F,G, F 和 G 之间无非零扩张当且仅当 G∈Dom(F).

证明假设G∈Dom(F), 根据定义, 存在 m,n∈N使得

Hom(τmG,F)≠0,Hom(F,τ-nG)≠0,

Hom(τm-1G,F)=0,Hom(F,τ-n+1G)=0.

根据引理1, 如果Hom(F,τG)≠0,则Hom(F,τ-n+1G)≠0, 与假设矛盾. 故Hom(F,τG)=0. 同理可得,Hom(G,τF)=0. 所以有Ext1(F,G)=Ext1(G,F)=0.

反之,已知F,G之间无非零扩张,若G∉Dom(F),则对于任意的m∈N,τmG∉S(→F)或者τ-mG∉S(F→).不妨设当m≥0时,τmG∉S(→F).根据vect(X)的结构可知,存在n∈N+使得τ-nG∈S(→F),进而Hom(τ-n+1G,F)≠0.当n=1时,τ-1G∈S(→F),即Hom(G,τF)≠0;当n>1时,Hom(G,τn-1F)≠0,根据引理1,Hom(G,τF)≠0.综上,根据Serre对偶,这表明了Ext1(F,G)≠0,与F,G之间无非零扩张矛盾.假设不成立,引理得证.

接下来,通过考察权投射线的凝聚层范畴上的任意倾斜丛,给出本文的主定理:

定理1给定T是coh(X)中的任意倾斜丛, 则T的不可分解直和项落在不同的τ-轨道上, 且直和项的个数为p+q. 进一步地, 在vect(X)的Auslander-Rieten箭图中,T和slice一一对应.

证明设L是任意的不可分解丛, 对任意的n∈N，根据Serre对偶,

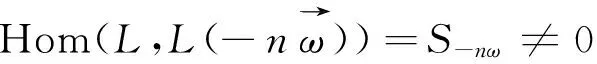
参考文献：

[1]GEIGLEW，LENZINGH.Aclassofweightedprojectivecurvesarisinginrepresentationtheoryoffinitedimensionalalgebras[J].Singularities,RepresentationsofAlgebras,andVectorBundles,SpringerLectNotesMath,1987,1273:265-297.

[2]CHENJ,LINY,RUANS.Tiltingbundlesandthemissingpartonaweightedprojectivelineoftype(2,2,n)[J].JPureApplAlgebra,2015,219(7):2538-2558.

[3]LENZINGH,REITENI.HereditarynoetheriancategoriesofpositiveEulercharacteristic[J].MathematischeZeitschrift,2006,254(1):133-171.

[4]RINGELCM.Tamealgebrasandintegralquadraticforms[M].Berlin:SpringerLect,1984:180.

doi：10.6043/j.issn.0438-0479.201507026

收稿日期：2015-07-20录用日期：2016-01-08

*通信作者：jinjingchenyu@126.com

中图分类号:O 154.1

文献标志码：A

文章编号：0438-0479(2016)04-0547-03

Tilting Bundles in the Category of Coherent Sheaves over Weighted Projective Lines with Weight Type (p,q)

CHEN Jinjing*,LIN Yuna

(School of Mathematical Sciences,Xiamen University,Xiamen 361005,China)

Abstract:In this paper we investigate the behavior of tilting bundles in the category of coherent sheaves over weighted projective lines with weight type (p,q). We prove that the canonical tilting bundle always forms a slice in the Auslander quiver, and then we describe the structure of the category of vector bundles. Furthermore we identify some properties of vector bundles from the aspects of indecomposable objects, slice, level, and domain among others. Finally it is shown that there is a bijection between all tilting bundles and slices.

Key words:weighted projective line;tilting bundle;slice

引文格式：陈金晶,林玉娜.(p,q)型权投射线的凝聚层范畴上的倾斜丛[J].厦门大学学报(自然科学版)，2016,55(4)：547-549.

Citation：CHEN J J,LIN Y N．Tilting bundles in the category of coherent sheaves over weighted projective lines with weight type (p,q)[J].Journal of Xiamen University(Natural Science)，2016,55(4)：547-549．(in Chinese)