峨眉黄山石灰石矿台阶边坡爆破振速安全阀值研究

余海兵， 胡　斌， 冉秀峰， 李　俊， 祝　凯

(中国地质大学 工程学院，武汉　430074)



峨眉黄山石灰石矿台阶边坡爆破振速安全阀值研究

余海兵， 胡斌， 冉秀峰， 李俊， 祝凯

(中国地质大学 工程学院，武汉430074)

摘要：爆破振速幅值的控制对边坡的稳定性起着重要的作用，以峨眉黄山石灰石矿山台阶边坡为例，采用拟静力法研究含软弱层边坡，倾角θ=15°～34°，临界高度H=5～14 m在安全系数为1.1情况下的安全阀值；采用应力判别法得出灰岩的安全阀值；采用FLAC3D有限差分法对边坡进行动力响应分析，对边坡关键监测点的位移，塑性区云图、剪应变增量云图、关键点的主振速度进行综合分析，得出边坡在临界状态下的安全阀值；通过对算例的研究分析得出，拟静力法得出的安全阀值和数值模拟动力分析的计算结果接近，互相印证了对安全阀值的取值比较合理。最后综合以上三种方法对爆破振速安全阀值进行合理取值。

关键词：爆破振动；安全阀值；拟静力法；应力判别法；有限差分法；台阶边坡

峨眉黄山石灰石矿山(见图1)历史上发生过多次大规模的顺层滑坡，其中爆破振动对边坡所造成的破坏作用是其中的很重要的一个诱因[1]。

爆破振速幅值的控制对边坡的稳定性起着重要的作用，目前国内外的行业规范多以质点的振速作为矿山爆破开挖的衡量标准，但是在阀值的选取上却并不一致，这主要是现场工程地质条件的千差万别，要制定一个具有普适性的标准是很困难的[2]。因此制定出适合实际情况的安全阀值显得非常重要。

目前，边坡动力稳定性的研究主要有拟静力法、应力判别法、室内试验法、数值模拟法。拟静力法将爆破荷载按等效静力来考虑进行极限平衡计算。给出直观判断边坡安全与否的定量性指标(安全系数)。不足之处是无法进行应力-变形分析，在简化过程也引入了一些不确定因素，使该法的可信度受影响。

近年来随着计算机技术的飞速发展，基于有限差分法的FLAC3D数值模拟软件以其程序特有的优势，很容易模拟动力问题，如振动、失稳、大变形等，而获得广泛应用。不足之处是前处理功能较弱，计算时步受网格尺寸影响较大和某些模式下计算时间过长。

本文尝试结合拟静力法、应力判别法、FLAC3D有限差分法三种方法对安全阀值的取值进行研究，综合得出矿山边坡的爆破振速安全阀值。

图1　峨眉黄山石灰石矿山图Fig. 1 Diagram of Emei mount Huangshan limestone mine

1工程地质概况

峨眉黄山石灰石矿区位于四川盆地边缘低中山地段，总体地形为南高、北低，单斜构造。海拔约500～1 229.1 m，矿山灰岩内不规律发育有多组软弱夹层，倾向与岩层一致，倾角上陡下缓，范围在15°～34°之间；历史上由于不规范的硐室爆破开挖，导致发生过多起滑坡。东滑坡、西滑坡均是沿软弱层滑动的。经现场测量倾角大约为21°～26°；矿山开采方式为：由东往西推进、先上后下开挖，台阶边坡角为70°，台阶高度15 m。 天然状态下岩体物理力学参数见表1。

表1　岩体物理力学参数

2拟静力法计算模型及参数选取

矿山岩体台阶边坡角α=70°，软弱层倾角选取θ=15°、22°、28°、34°(由上至下有代表性的不同高程倾角)，临界高度取H=5～14 m，计算模型及边坡参数见图2。

图2　边坡稳定性计算模型Fig.2 Model of the slope stability calculation

拟静力法计算边坡稳定性系数公式为：

(1)

由三角关系可得：

(2)

式中：γ为滑体的重度，H为临界高度，θ为软弱层倾角，α为台阶边坡角。

在考虑爆破振动的作用时，通常将爆破振动力等效为指向坡外的静力，其计算公式如下[3-4]：

FB=BbGa/g

(3)

式中：FB为等效的爆破振动力，Bb为爆破振动折减系数，一般在0.1～0.3之间取值，本文取0.2；G为滑体重量；a为爆破振动加速度；g为重力加速度。当质点作简谐运动时，a与v的关系为：

a=2πfv

(4)

式中：f为主振频率，通过现场爆破(逐孔微差爆破)实测，主要范围10～30 Hz，计算时取平均值20 Hz，v(cm/s)为质点主振速度。

拟静力法将爆破荷载按等效静力来考虑进行极限平衡计算，而没有考虑相位差等因素，从这个角度来看的话计算结果偏安全，所以安全系数可以适当的降低，但考虑到矿山爆破开挖作业频繁并且时间长达30年之久，会对岩体产生累计损伤的作用，弱化岩体力学参数。因此安全系数必须留有一定的安全储备。

综合考虑相关规范规程和标准，确定台阶边坡在爆破振动作用下的安全系数取值为1.1，根据拟静力法反算求得临界高度H、岩层倾角θ不同时对应的爆破振速安全阀值，计算结果见图3。

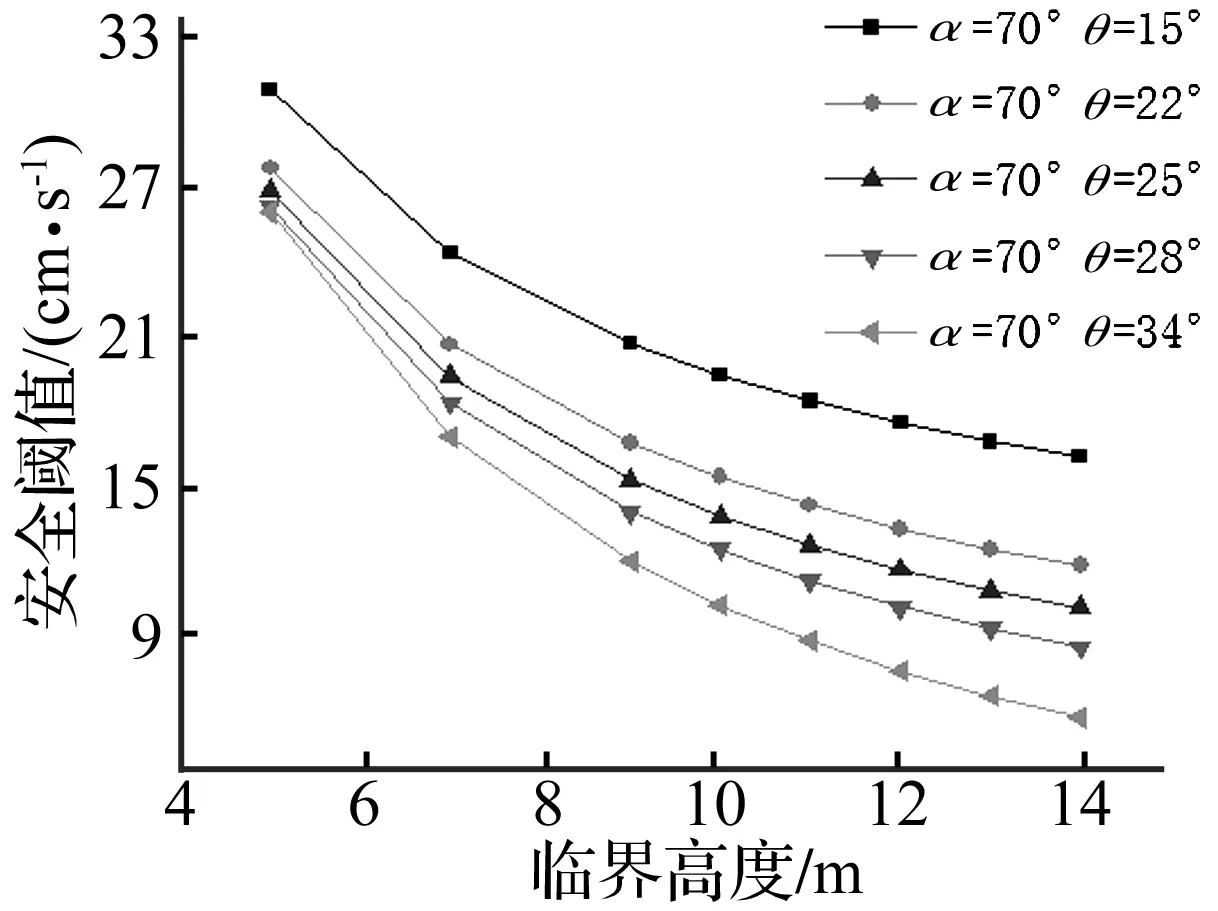
图3　临界高度与安全阀值的关系Fig.3 Relationship between security threshold and critical height

由图3可以看出：① 当临界高度相同时，岩层越陡对应的安全阀值越小；② 当岩层角度相同时，临界高度越大对应的安全阀值越小。

3应力判别法

依据一维应力波理论，爆破振动引起的动应力为：

σ=ρCpV

(5)

式中：ρ为岩体密度，kg/m；Cp为纵波速度，m/s;V为质点水平振动速度，cm/s。将岩体内质点动应力与岩体的抗拉强度进行比较，如果质点动应力超过了岩体的抗拉强度，则岩体因为爆破振动而破坏。由于爆破时间非常短，因此近似以静抗拉强度等效动抗拉强度，求得，灰岩的爆破振速安全阀值约为22 cm/s。

综合拟静力法和应力判别法可知：① 根据应力判别法求出的灰岩的爆破振速的安全阀值为22 cm/s，而根据拟静力法求得的安全阀值部分大于22 cm/s，由于拟静力法没有考虑应力应变的因素，可能导致部分安全阀值取值不合理，而根据应力判别法求得的安全阀值也是一种近似值，因此本文拟将再结合FLAC3D有限差分法进行动力分析研究，综合对矿山爆破振速安全阀值进行优化；② 由计算得出的规律可知矿山边坡的安全阀值并不是固定不变的，对于峨眉黄山石灰石矿台阶边坡，由于石灰岩内发育有软弱层，岩层倾角有变化，其控制着边坡的稳定，所以安全阀值的选取应针对软弱层倾角的变化取对应的值比较符合实际情况。研究得出的规律为数值模拟提供借鉴。

4数值模拟计算模型及参数选取

4.1模型概述

岩质边坡，岩质边坡软弱层厚度为0.5 m，其他参数见图4所示，边界范围满足静力和动力条件下的计算精度[5]。灰岩网格尺寸最大为2.5 m，满足大于输入波波长的1/8～1/10的要求[6-7]。

图4　边坡动力分析数值模型和监测点位置分布 (m)Fig.4 Dynamic numerical simulation model of the slope and location distribution of monitoring points(m)

4.2计算载荷及边界条件

岩体为弹塑性材料，采用摩尔库伦强度准则。局部阻尼为0.15，动力计算时，爆破波施加在模型左边界，输入的波形为现场实测的水平方向和竖直方向代表性波形(主频约为20 Hz，持续时间为0.85 s)，由于爆破振动波频率范围较广，输入前对振动波进行了滤波与基线校正处理，处理后的波形见图5，计算时根据需求按比例调整振幅大小。

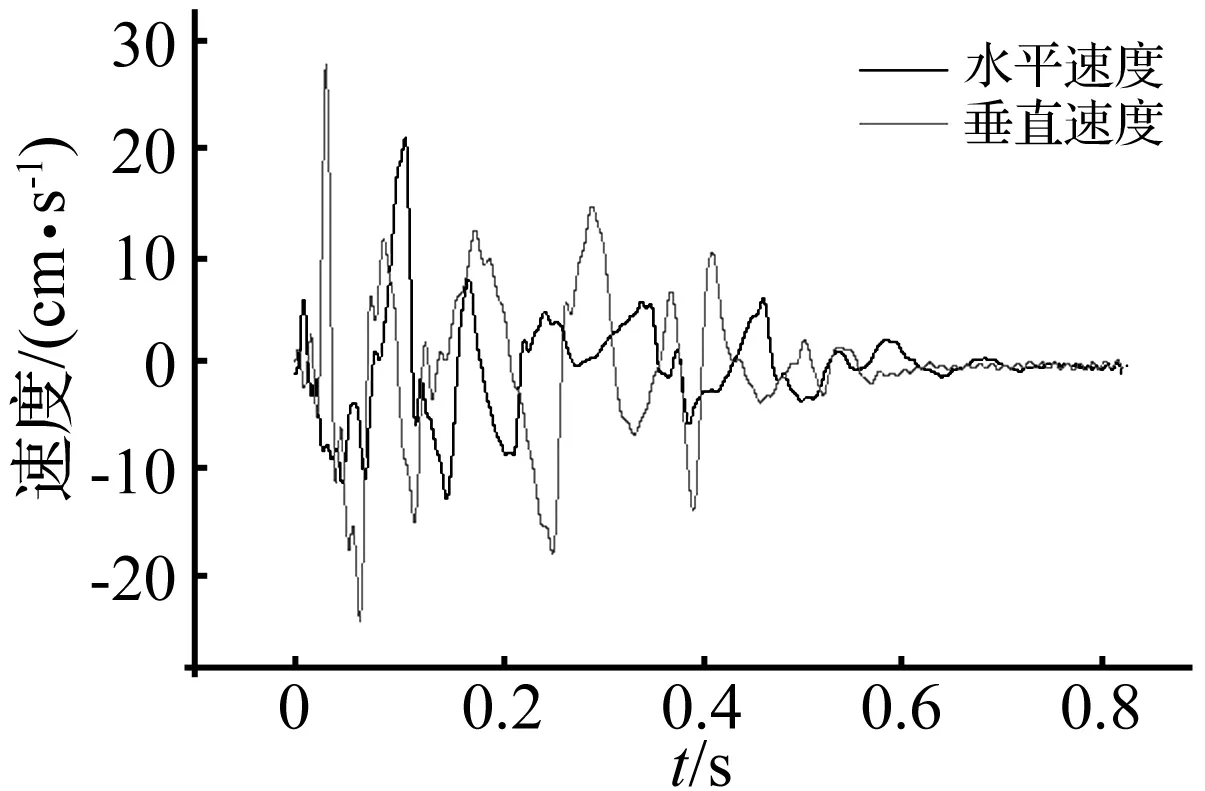
图5　爆破振动速度时程曲线Fig.5 Time history of velocity obtained by site monitoring

为了减小边界反射波的影响，设置为黏滞边界，将速度时程波转化为应力时程波[8]，施加于左边界；先进行静力计算得到重力作用下的初始应力场，再初始化位移进行动力计算[9-10](岩石物理力学参数见表1)。

为了研究岩体在爆破荷载作用下的稳定性，在具有代表性的部位设置了7个监测点(点1～点7)，见图4；动力计算时将点1的速度时程与输入波的时程图对比，发现吻合很好。说明波形的输入方式是准确的[11]。

4.3数值模拟计算结果

根据拟静力法的计算结果可知，临界高度H=14 m时，各软弱层倾角对应下的安全阀值最小，此种情况下的边坡最危险，下面主要以H=14 m，软弱层倾角θ=15°为例建立数值模型进行动力分析。 调整输入波的振幅，进行试算，现将计算结果进行分析和阐述。

4.3.1监测点(点2～点5)水平位移分布

图6为四个监测点的位移时程图，从图可以看出：软弱层上的灰岩和软弱层下的灰岩位移方向不一致，结构面控制着边坡的动力响应，软弱层之上岩体并未产生整体性的移动，位移表现为坡底>坡腰>坡顶，位移较小，数量级为10-3m，计算收敛，说明潜在滑体最终稳定。

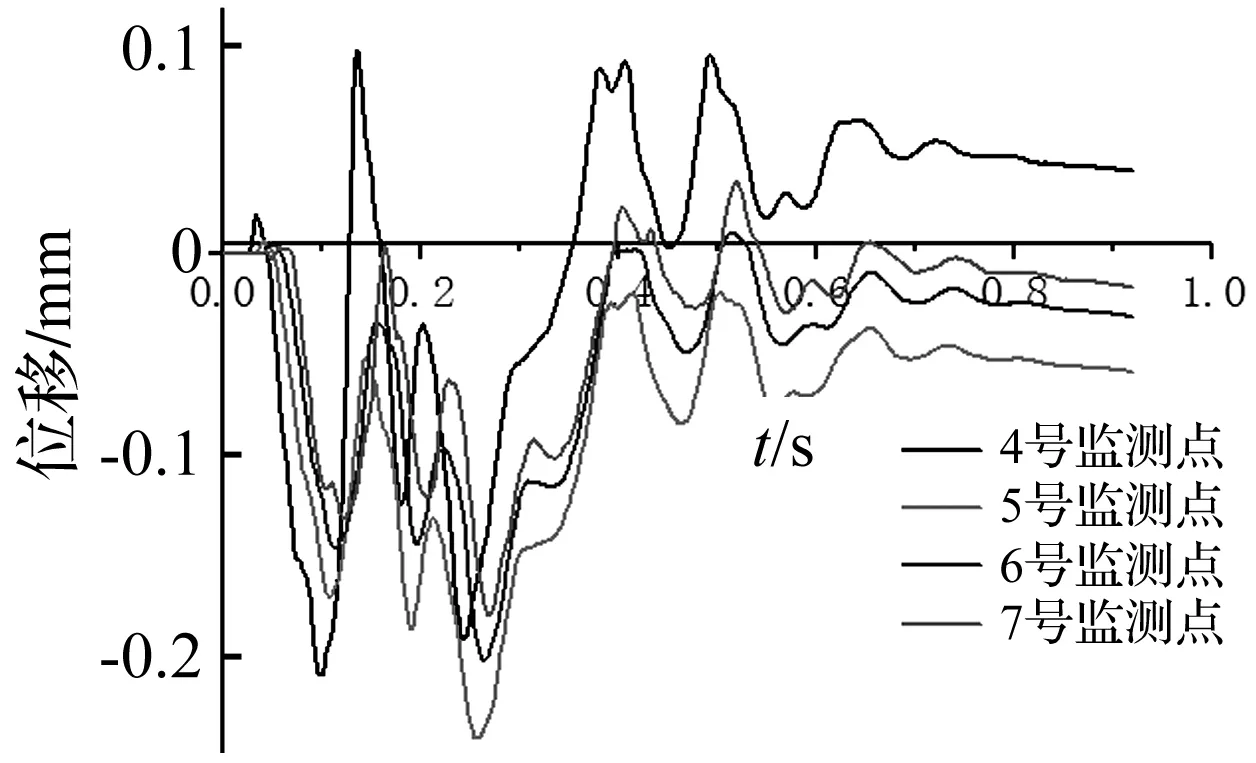
图6　监测点水平向位移时程曲线Fig.6 The time-dependent curve of horizontal displacement of monitoring points

4.3.2边坡塑性区分布

由图7可以看出：下部台阶靠近爆源处有较大范围受拉应力屈服状态，说明在此输入爆破荷载作用下，爆源附近边坡岩体会产生一定的爆破损伤，可能会发生局部垮塌；通过对监测点提取数据，得到：2号监测点的最大速度为50 cm/s，3号监测点的最大速度为25 cm/s，4号监测点的速度为19 cm/s，3号监测点至4号监测点之间基本无塑性区，说明利用应力判别法得出灰岩的安全阀值22 cm/s比较安全；软弱层岩体剪切屈服和受拉应力屈服，塑性区贯通，表明爆破振动波已对软弱夹层产生了一定的不利影响，结合图6可知软弱层上部岩体在振动波的作用下会产生反复错动，并最终向坡外产生了较小的永久位移，因此原本岩性比较软弱的软弱夹层就会因上部岩层的反复错动而开裂，造成结构面的增加和扩展，从而降低软弱夹层的抗剪和抗拉强度。

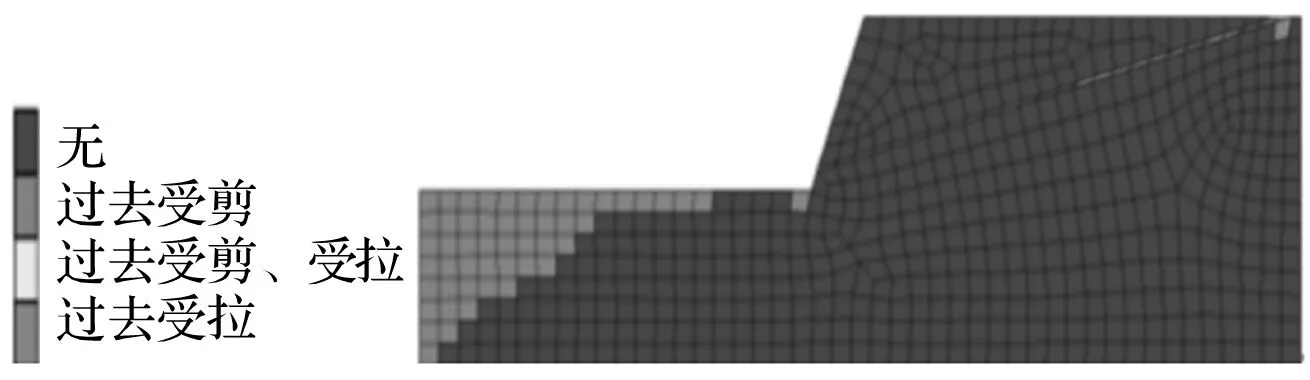
图7　爆后边坡体内塑形区分布图Fig.7 Plastic zones of rock slope after blasting

4.3.3剪应变增量分布图

从图8可以看出：剪应变增量带主要出现在爆源附近岩体和软弱层上，软弱层出现了剪应变增量最大为1.54E-003的区域，主要集中在软弱层内，剪应变集中带即将贯通，说明边坡即将可能发生整体性的错动，处于一种相对稳定的临界状态。

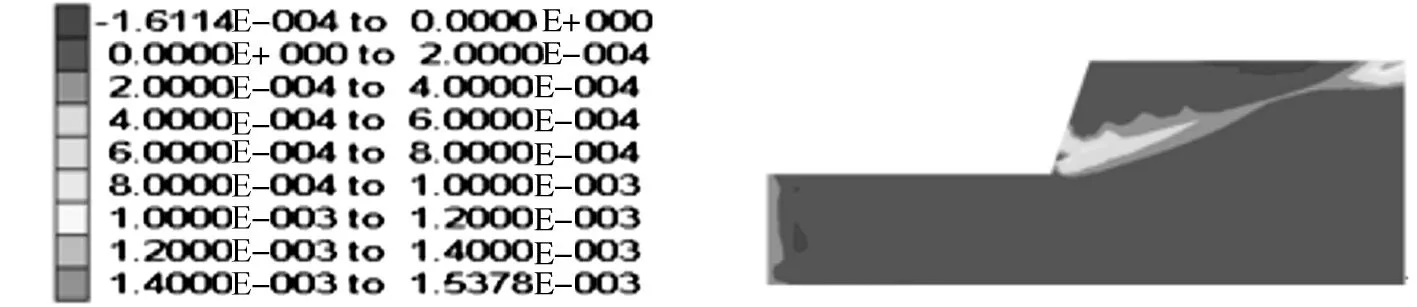
图8　爆破后坡体内剪应变增量云图Fig.8 Nephogram of the shear strain increment after blasting

4.3.4监测点(点4～点7)速度时程图

从图9可以看出：软弱层之上的岩体和软弱层之下的岩体速度差别较大，结构面控制着边坡的动力响应，软弱层之上岩体的振速，坡底<坡腰<坡顶，表现出了高程放大效应[12-13]。计算结果收敛，边坡稳定。

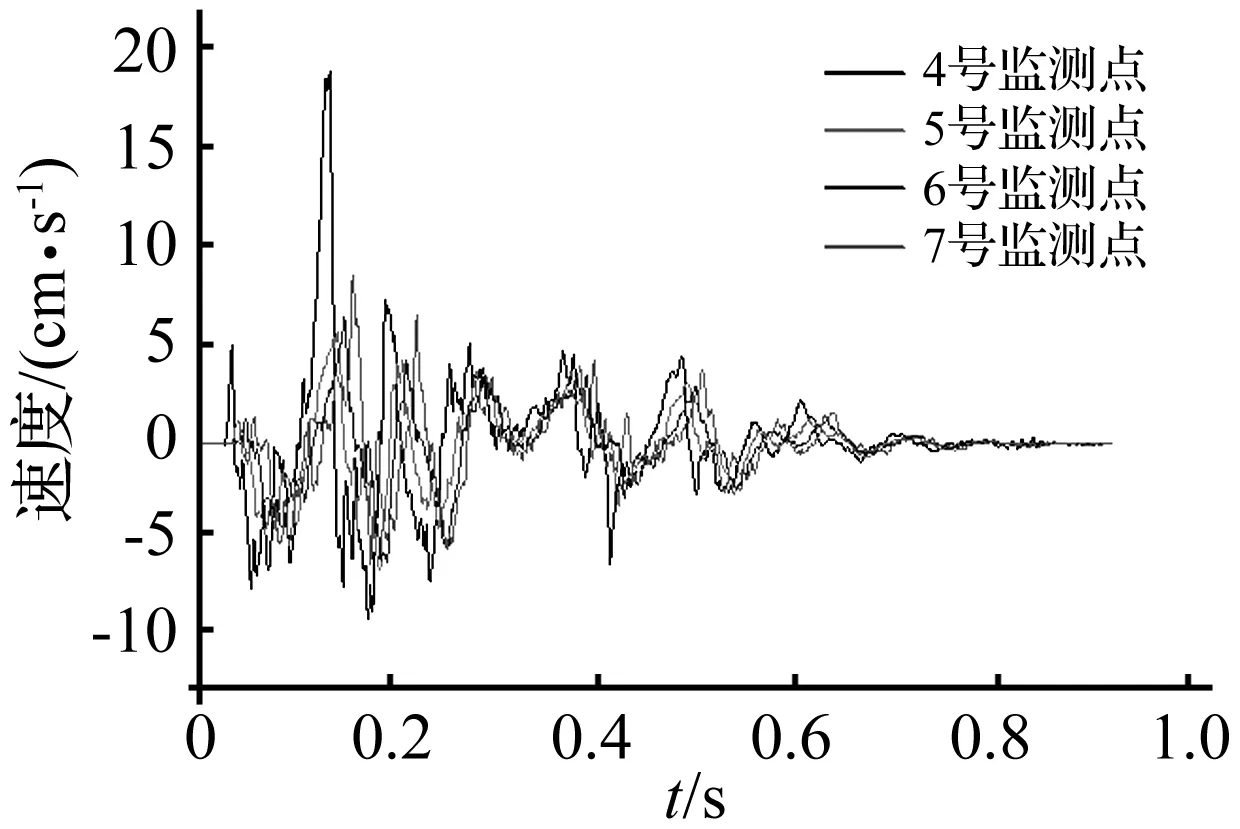
图9　监测点水平向速度时程曲线Fig.9 The time-dependent curve of horizontal velocity of monitoring points

综合图6～图9可知，在此输入的爆破荷载作用下，靠近爆源处边坡很可能会发生拉伸破坏，发生垮塌，坡脚部位极小塑性区，坡脚稳定；对边坡内的软弱层有一定的爆破损伤，边坡处于即将滑动的相对稳定的临界状态。由于在数值模拟的计算过程中并没有将爆破累计损伤的影响考虑进去，因此在静力情况下是稳定的话，一般对于动力计算，如果没有将岩体力学参数的劣化更新进去，计算是偏安全的，计算结束后，潜在滑体的速度和位移是收敛的，只是会产生一定的永久位移，按照动力失稳的判据来说，边坡最终是稳定的。

由于矿山爆破作业频繁，年限长久，如果振速安全阀值没有控制好，特别是对于终了边坡，频繁的爆破振动就会导致潜在滑体永久位移的累积，而岩层的错动也必导致岩体结构面的扩展和贯通，雨水顺着结构面错动后的通道渗入后对软弱层的软化和泥化作用，将导致其岩体力学参数持续的降低，综合因素的作用下，最终就极有可能导致边坡的失稳破坏，这也是峨眉黄山石灰石矿山边坡曾经发生多起滑坡的重要原因之一，因此对于安全阀值的取值必须严格控制。

根据以上分析结果，考虑到安全生产的需要，安全阀值的取值应小于潜在滑体底部(4号监测点)的速度振幅19 cm比较合理。由拟静力法反算求得在满足安全系数1.1情况下的安全阀值为16.3 cm/s，两者较为接近，互相印证。综合取安全阀值为17 cm/s。

分析过程同上，求得H=14 m，θ=22°、θ=28°的安全阀值分别为14 cm/s、 8.5 cm/s。并试算了部分其它情况，发现数值模拟的计算结果和拟静力法的计算结果相差不大，起到了互相印证的效果，拟静力法的计算结果较为可靠，其余部分可参考拟静力法的研究结果，并结合一维应力波的应力判别法，来快速确定安全阀值。经过综合研究，得出矿山边坡的安全阀值，见图10。

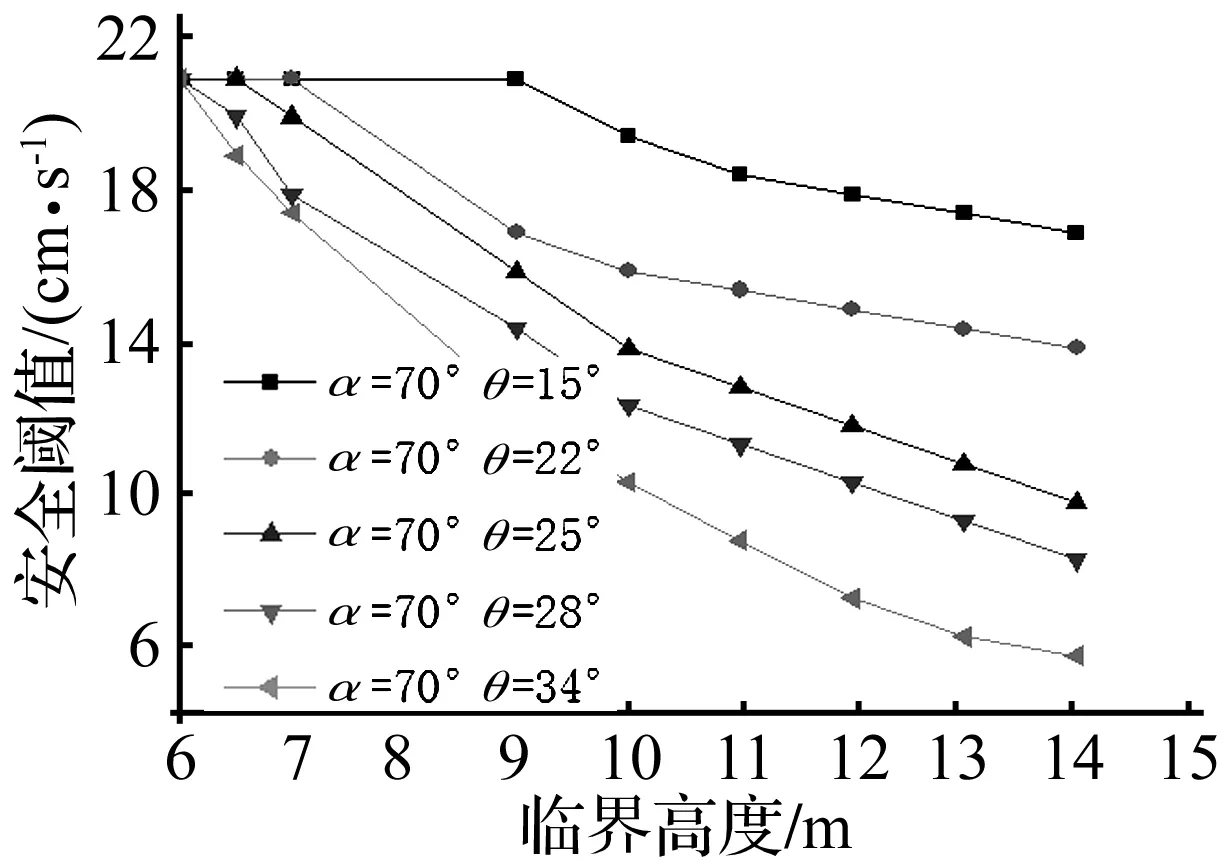
图10　临界高度与安全阀值的关系Fig.10 Relationship between security threshold and critical height

根据现场爆破实测得出的撒道夫斯基回归公式，即可得出单段最大药量和安全距离的关系，用于指导矿山安全生产。

5结论

(1) 矿山边坡的爆破振速安全阀值并不是一个固定值，对于含软弱层的边坡，它跟软弱层的倾角和临界高度相关，应该根据其倾角和临界高度的变化，制定相应的安全阀值；软弱层控制着边坡的动力响应，对于含软弱层的边坡以坡脚的振速为标准，确定安全阀值。

(2) 拟静力法由于不能进行应力-变形分析，在简化过程也引入了一些不确定因素，导致部分安全阀值取值不合理，可以结合应力判别法和数值模拟的分析结果，进行综合取值。在此经验基础上，确定类似情况下的安全阀值，避免了多次重复建模试算，提高了效率。

(3) 数值模拟法分析得出的爆破振速安全阀值可以根据边坡关键监测点的位移、塑性区云图、剪应变增量云图、关键点的主振速度综合确定。

(4) 尽量避免雨天作业，并作好排水措施、安全措施，当爆破开挖时，若有软弱层出露，条件允许时建议先将含软弱层的岩体开挖，使安全阀值增大到21 cm/s，从而增大爆破规模，并有利于矿山的生产安全。

参 考 文 献

[1] 唐剑.露天深孔台阶爆破地震效应试验研究与数值模拟[D].成都：西南交通大学,2006.

[2] 许红涛.岩石高边坡爆破动力稳定性研究[D].武汉：武汉大学，2006.

[3] 李祥龙，庙延钢，杨溢，等. 爆破震动对边坡稳定性影响分析[J].爆破,2006,23(4):15-19.

LI Xiang-long, MIAO Yan-gang,YANG Yi, et al. Slope stability analysis under influence of blasting vibration[J].Blasting,2006,23(4):15-19.

[4] 林大能，唐业茂，范金国，等.爆破震动作用下高陡边坡稳定性分析[J].矿业工程研究,2009, 24(1)：25-28.

LIN Da-neng, TANG Ye-mao, FAN Jin-guo, et al. Slope stability under the action of vibration induced by blasting [J].Mineral Engineering Research, 2009, 24(1):25-28.

[5] 徐光兴，姚令侃，李朝红，等.边坡地震动力响应规律及地震动参数影响研究[J].岩土工程学报，2008，30(6)：918-923.

XU Guang-xing, YAO Ling-kan, LI Zhao-hong,et al. Dynamic response of slopes under earthquakes and influence of ground motion parameters[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(6): 918-923.

[6] Itasca Consulting Group Inc.FLAC-2D.Version 5.00.Users Manual(Volume V)[R].USA：Itasca Consulting Group Inc,2005.

[7] 陈建平，高文学，陶连金.爆破工程地质控制论[J].工程地质学报，2006,15(5)：616-619.

CHEN Jian-ping,GAO Wen-xue,TAO Lian-jin.Theory of rock blasting control in geology engineering[J].Journal of Engineering Geology,2006,15(5):616-619.

[8] 夏详，李俊如，李海波,等.爆破荷载作用下岩体振动特征的数值模拟[J] .岩土力学，2005,26(1)：50-56.

XIA Xiang, LI Jun-ru, LI Hai-bo, et al. Udec modeling of vibration characteristics of jointed rock mass under explosion[J]. Rock and Soil Mechanics, 2005,26(1)：50-56.

[9] 郑颖人，叶海林，黄润秋.地震边坡破坏机制及其破裂面的分析探讨[J].岩石力学与工程学报，2009,28(8):1714-1723.

ZHENG Ying-ren,YE Hai-lin, HUANG Run-qiu.Analysis and discussion of failure mechanism and fracture surface of slope under earthquake[J].Chinese Journal of Rock Mechanics and Engineering, 2009,28(8):1714-1723.

[10] 赵宝云, 刘保县, 万贻平. 爆破震动对某边坡稳定性影响的数值模拟[J]. 工程地质学报, 2008, 16(1): 59-62.

ZHAO Bao-yun, LIU Bao-xian, WAN Yi-ping. Numerical simulation of blasting vibrationon slope stability[J]. Journal of Engineering Geology, 2008, 16(1):59-62.

[11] 言志信,张森,张学东,等.顺层岩质边坡地震动力响应及地震动参数影响研究[J].岩石力学与工程学报，2011(增刊2):3522-3528.

YAN Zhi-xin, ZHANG sen, ZHANG Xue-dong, et al. Study of dynamic response of bedding rock slope under earthquake and influence of ground motion parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2011(Sup2):3522-3528.

[12] 付波,胡英国,卢文波,等.岩石高边坡爆破振动局部放大效应分析[J].爆破,2014,31(2):2-7.

FU Bo, HU Ying-guo, LU Wen-bo, et al. Local amplification effect of blasting vibration in high rock slope[J].Blasting, 2014, 31(2): 2-7.

[13] 蒋楠,周传波,平雯,等.岩质边坡爆破振动速度高程效应[J].中南大学学报:自然科学版, 2014(1): 238-243.

JIANG Nan, ZHOU Chuan-bo, PING Wen, et al. Altitude effect of blasting vibration velocity in rock slopes[J]. Journal of Central South University:Science and Technology, 2014(1): 238-243.

基金项目：国家自然科学基金项目资助(4117281);国家科技部973项目资助(2011CB710604)；中央高校基本基金业务费专项资金项目资助 (摇篮人才计划CUGL100413);特色学科团队(CUG090104)

收稿日期：2015-06-10修改稿收到日期：2015-07-27

通信作者胡斌 男，博士，教授，博士生导师，1974年生

中图分类号:TU457

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.020

Safety threshold of blasting vibration velocity on the slope of Ermei mount Huangshan limestone stairs

YU Hai-bing, HU Bin, RAN Xiu-feng, LI Jun, ZHU Kai

(Faculty of Engineering, China University of Geosciences, WuHan 430074, China)

Abstract:For the slope stability, the amplitude of blasting vibration velocity plays an important role. A case study on the safety threshold of Ermei mount Huangshan limestone bench slope was carried out, which uses the pseudo-static method in the analysis of the slope with weak layer under the condition of dip θ=15°～34°, critical height H=5～14 m and safety factor=1.1. In addition, the safety thershold of limestone was also determined according to the stress criterion. Then, the FLAC3Dfinite difference method was adopted to analyse the dynamic response of the slope, displacement of the slope at key monitoring points, plastic area cloud, shear strain increment cloud and main vibration velocities at key points, and the slope safety threshold in the critical state was achieved. Based on the results of the case study, the safety thresholds, calculated respectively by the pseudo-static method and the dynamic numerical simulation are in good agreement, and the values of the safety threshold are mutually verified to be reasonable. Finally, the above three methods were summarized to get a reasonable value of the safety threshold of blasting vibration velocity.

Key words:blast vibration; safety threshold; quasi-static method; stress criterion; finite difference method; bench slope

第一作者 余海兵 男，硕士，1987年生