轴向运动变截面黏弹性梁的振动与稳定性分析

李成澄, 赵凤群

(西安理工大学 理学院,西安　710054)



轴向运动变截面黏弹性梁的振动与稳定性分析

李成澄, 赵凤群

(西安理工大学 理学院,西安710054)

摘要：由D’Alembert 原理，建立了轴向运动黏弹性变截面梁的运动微分方程，给出了一种重心有理插值DQ法的数值求解方法。对于简支黏弹性变截面梁，用该方法得到了特征方程，获得了变截面梁前两阶无量纲复频率与无量纲轴向运动速度的变化关系。分析了梯形截面梁和抛物形截面梁随轴向运动速度变化的失稳形式，并与等截面梁进行了比较，同时分析了变截面梁的高度比和黏弹性系数对梁动力稳定性的影响。

关键词：变截面梁；黏弹性；轴向运动；稳定性；DQ法；复频率

近年来，学者们对轴向运动梁、板等结构的稳定性问题进行了大量研究，Mote等[1-5]研究表明，物质的轴向运动将引发横向振动，且振动强度与初始轴力、运动速度等有着密切的关系，当运动速度超过临界速度时，会导致模态失稳。Lee等[6]用谱分析方法研究了均匀张力作用下轴向运动Timoshenko梁的横向振动特性。赵凤群等[7]建立了轴向运动FGM Timoshenko梁的运动微分方程组，采用WDQ法，获得了简支FGM梁的复频率，分析了轴向运动FGM Timoshenko梁在不同长高比和梯度指标下的振动特性。Mergen等[8-9]研究了轴向运动梁在变速运动下的横向振动稳态响应，他们还研究了在屈曲状态下轴向运动黏弹性梁的非线性动力特性。梁是结构工程中的基本构件，随着科技的发展，变截面梁的优势日益突出，在机械、航空、建筑等领域有着广泛的应用前景。针对变截面梁的振动特性，已经有不少的研究成果。Caruntu[10]研究了高度沿轴线方向，截面呈抛物型矩形变截面梁的非线性振动问题；Mehmet等[11]研究了梁的截面宽度沿轴线方向，截面为指定幂指数函数的变截面梁的振动特性。徐腾飞等[12]利用Frobenius 级数求解振动方程的近似解，获得了变截面梁振动问题的求解方法，但此方法不具有普遍通用性。但是对于轴向运动变截面梁的振动特性研究较少。

考虑到黏弹性材料的广泛使用，本文由D’Alembert原理，研究了轴向运动变截面黏弹性梁的振动与稳定性问题，以重心有理插值函数为基函数，采用DQ法求解，克服了传统DQ法节点增多即出现数值不稳定的缺点。

1控制微分方程的建立

考虑轴向运动变截面黏弹性梁，以轴向为x轴建立坐标系，单位长度密度为ρ(x)，截面面积为A(x)，梁长度为L，轴向运动速度为V。当梁垂直于x轴的截面为矩形，宽度为b，高度为h(x),x∈[0,L]时，截面面积A(x)=bh(x)。如当梁在xoz面上的截面是梯形，如图1(a)所示，这时

(1)

当梁在xoz面上的截面是抛物型，如图1(b)所示，这时

(2)

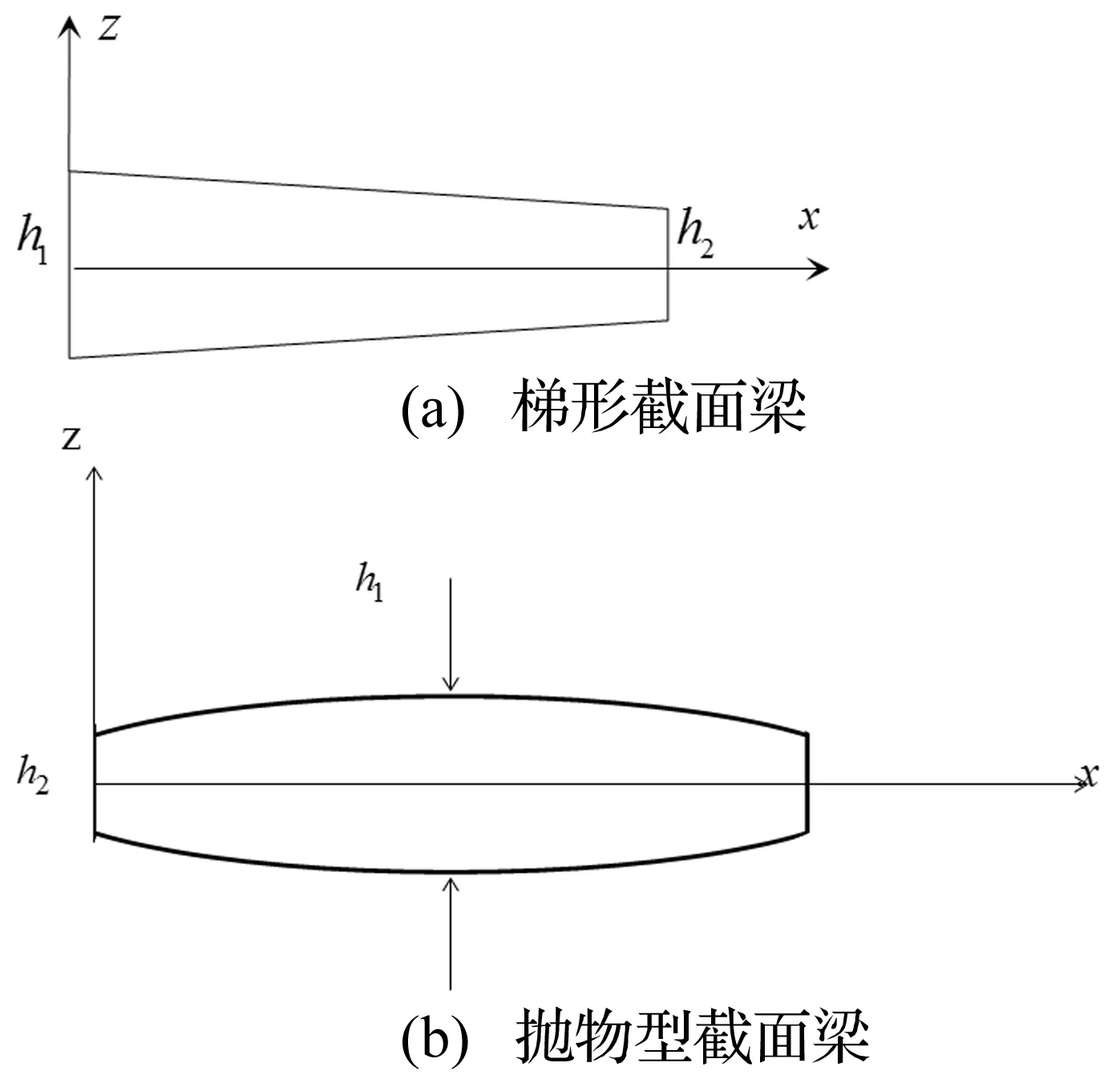
图1　变截面轴向运动梁Fig.1 Axially moving beam with varying section

假设黏弹性模型为Kelvin-Voigt 模型，即

(3)

式中:ε为轴向应力，E为材料的弹性常数，γ为黏弹性系数。对于小变形，应力-位移关系为

(4)

式中：w=w(x,t)是梁的横向位移。

梁的截面弯矩M为

(5)

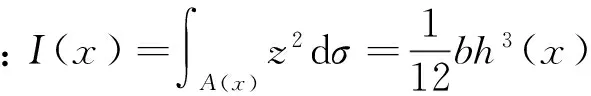
梁沿z轴方向的速度可以表示成

(6)

因此z轴方向的加速度为

(7)

由D’Alembert原理，我们可以获得轴向运动黏弹性梁的运动微分方程为

(8)

式中:P0为梁的初始张力。

将式(5)代入式(8)，可获得Kelvin-Voigt模型黏弹性变截面轴向运动梁的运动控制微分方程

(9)

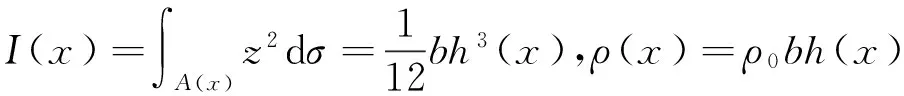
(10)

假设梁的两端是简支的，则边界条件为

w(0,t)=w(L,t)=0,

(11)

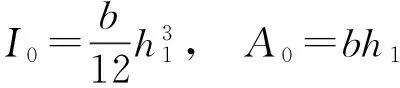
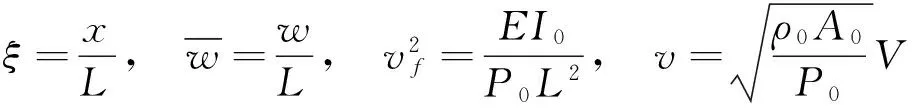
则式(10)可化成如下无量纲形式

(12)

边界条件为

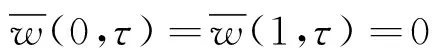
(13)

2稳定性分析

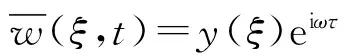
(14)

边界条件为

y(0)=y(1)=0,y″(0)=y″(1)=0

(15)

对于式(14)～(15)，本文选取重心有理插值基函数作为插值基函数，采用DQ法求解。

取重心有理插值基函数[13]

(16)

式中：wk为权重，且I={1,2,…,N}为一指标集。

计算格式如下

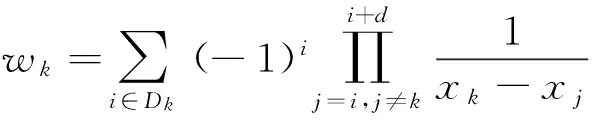
Dk={i∈I:0≤k-d≤i≤N-d}

(k=0,1,…N)

(17)

可见wk只依赖于节点。则一阶权系数可以表示如下

(18)

则由各阶导数的权系数之间的递推关系

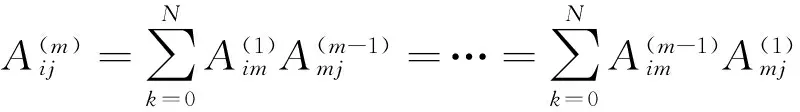
(i,j=0,1,…N)

(19)

将式(14)、(15)用微分求积法离散，得

(20)

令式(20)的行列式等于0，得到式(14)、(15)的特征方程，由特征方程可以求得无量纲复频率ω与无量纲速度v之间的关系，进而讨论轴向运动黏弹性梁的动力稳定性。

3数值结果及分析

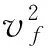
应用DQ法计算时，选取Gauss-Lobatto点，取N=20，局部结点个数d=5。

表1　等截面简支梁前二阶固有频率(v=2,　α=0)

3.1变截面轴向运动弹性梁稳定性分析

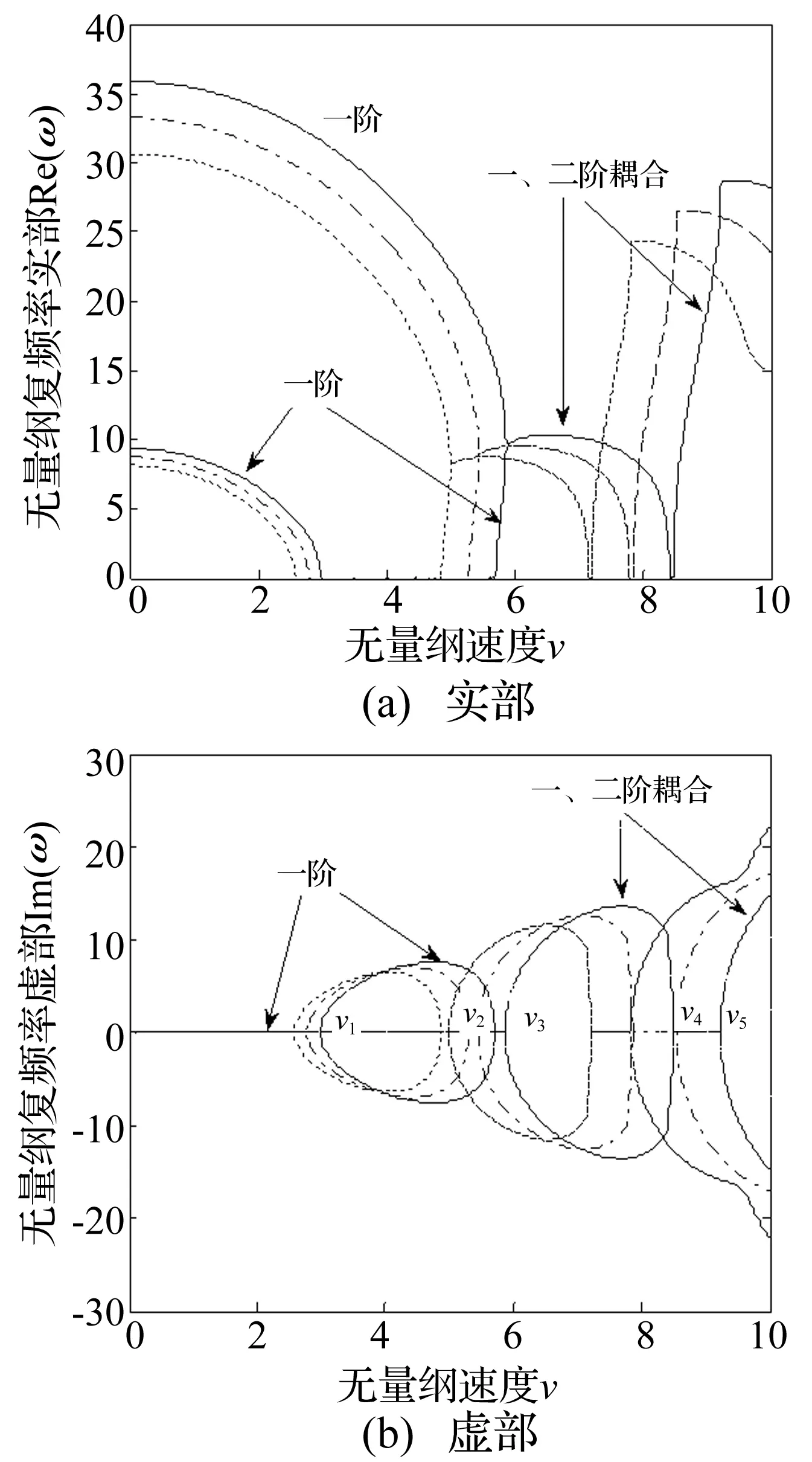
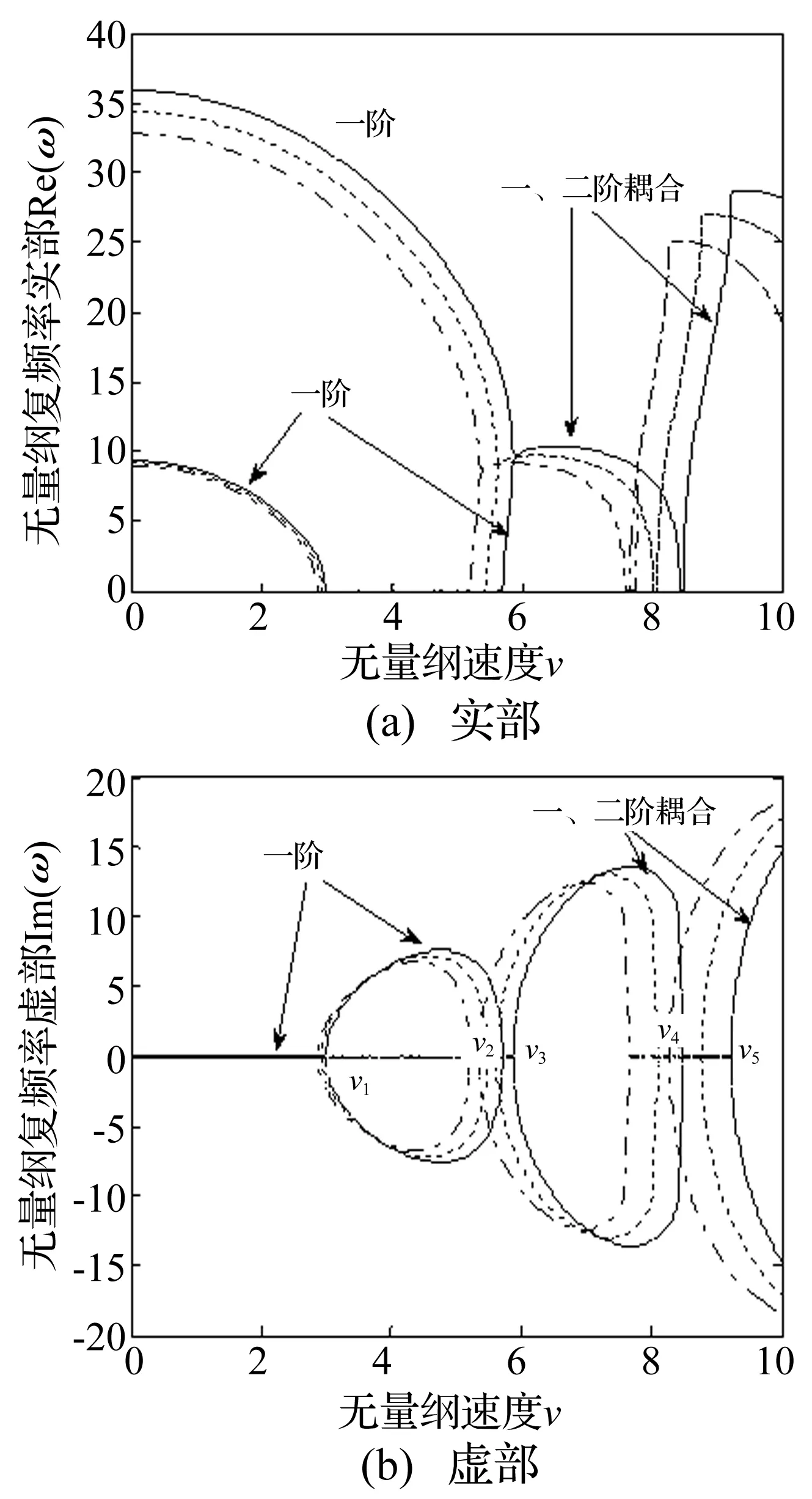
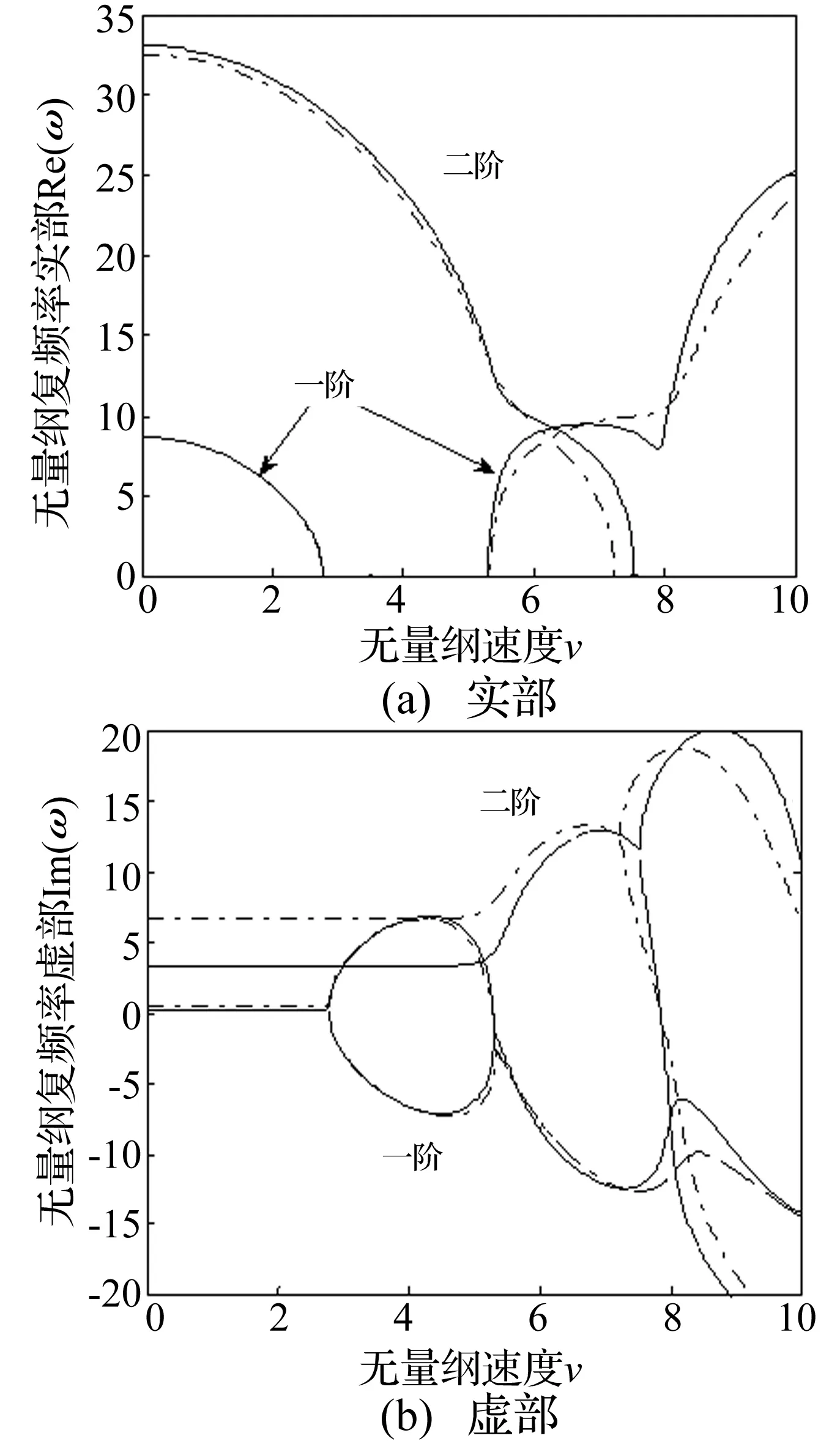
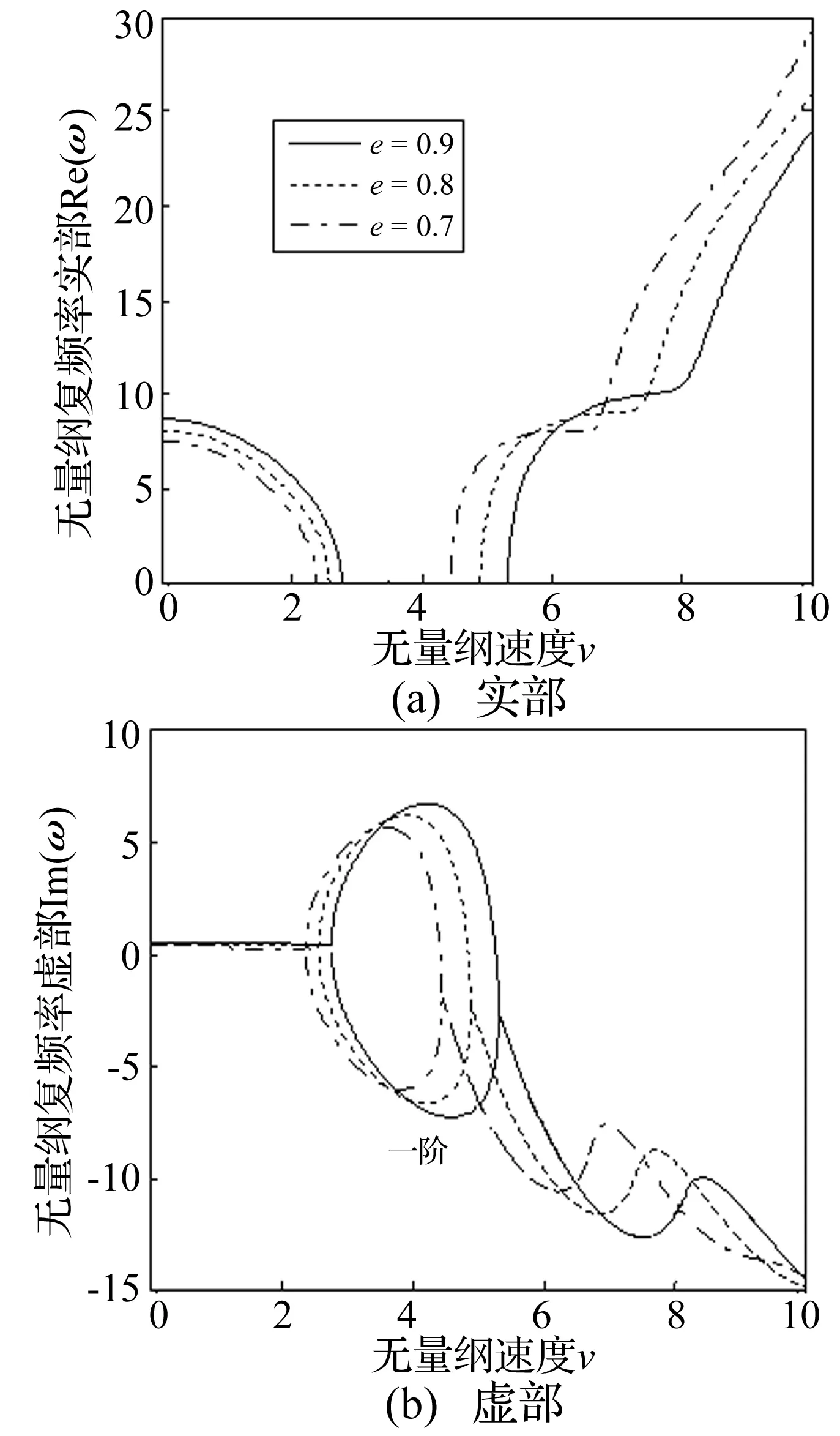
图2为轴向运动梯形截面简支弹性(α=0)梁在不同厚度比e=h2/h1下前二阶无量纲复频率随无量纲轴向运动速度的变化关系。对于等截面梁(e=1，图中实线表示)，当无量纲速度v

(—表示e=1；-·表示e=0.9；……表示e=0.8)图2　梯形截面梁前两阶复频率随轴向运动速度的变化曲线(e=1,0.9,0.8)Fig.2 Curves of the first two order complex frequencies of beam with trapezoid cross section vs. the moving speed(e=1,0.9,0.8)

当v3v5时，梁发生前两阶模态耦合颤振失稳，v5为颤振失稳临界速度。对于梯形截面梁(e=0.9,0.8)，其稳定性与等截面梁类似，但随着厚度比的减小，各阶失稳临界速度也在减小。

图3为轴向运动抛物形截面简支弹性梁在不同厚度比下前二阶无量纲复频率随无量纲轴向运动速度的变化关系。可以看出抛物形截面梁的振动稳定性与梯形截面梁类似，故以下只讨论以梯形截面梁。

(—表示e=1；-·表示e=0.9；……表示e=0.8)图3　抛物形截面梁前两阶复频率随轴向运动速度的变化曲线(e=1,0.9,0.8)Fig.3 Curves of the first two order complex frequencies of beam with parabolic cross section vs. the moving speed (e=1,0.9,0.8)

3.2变截面轴向运动黏弹性梁稳定性分析

图4为e=0.9时梯形截面梁在不同黏性系数α=0.005,0.01下前二阶无量纲复频率随无量纲轴向运动速度的变化关系。可以看出，对于黏弹性梁，已经不出现前两阶模态耦合现象。在一阶模态上，当无量纲速度v0，Im(ω1)>0，表明梁做衰减周期振动，处于稳定状态；当v1v2时，Re(ω1)≠0，Im(ω1)<0，表明梁出现颤振失稳，v2为颤振失稳临界速度。在二阶模态上，当无量纲速度v0，Im(ω1)>0，表明梁做衰减周期振动，处于稳定状态；当v>v1时，Re(ω1)=0，Im(ω1)≠0，表明梁出现二阶模态发散失稳。

(—表示α=0.005；-·表示α=0.01)图4　梯形截面梁前两阶复频率随轴向运动速度的变化曲线(e=0.9)Fig.4 Curves of the first two order complex frequencies of beam with trapezoid cross section vs. the moving speed(e=0.9)

图5　不同厚度比下梯形截面梁一阶复频率随轴向运动速度的变化曲线(α=0.01,e=0.9,0.8,0.7)Fig.5 Curves of the first order complex frequency of beam with trapezoid cross section vs. the moving speed(α=0.01,e=0.9,0.8,0.7)

可见黏弹性系数的大小基本不影响梁的一阶发散失稳临界流速值，但一阶颤振失稳临界流速值随着黏性系数的增大而增大，而二阶发散失稳临界流速值随着黏性系数的增大而减小。

图5为α=0.01时梯形截面梁在厚度比e=0.9,0.8,0.7下一阶无量纲复频率随无量纲轴向运动速度的变化关系。可见对同一黏性系数，随着厚度比的减小，一阶失稳临界流速值也在减小。

4结论

本文建立了轴向运动变截面黏弹性梁的运动微分方程，分析了简支梯形和抛物形黏弹性梁随轴向运动速度变化的振动特性和失稳形式，结论如下：

(1) 对轴向运动弹性梁，随着运动速度的增大，梁经历了稳定(等幅周期振动)-一阶发散失稳-再稳定-一、二阶模态耦合颤振失稳-再稳定-前两阶模态耦合颤振失稳的过程。梯形截面和抛物形截面梁的稳定性与等截面梁类似，随着厚度比的减小，失稳临界速度值也在减小。

(2) 对轴向运动黏弹性梁，随着运动速度的增大，梁经历了稳定(衰减周期振动)-一阶发散失稳-一阶模态颤振失稳的过程，没有一、二阶模态耦合现象。对同一种截面梁，黏性系数的大小基本不影响一阶发散失稳临界流速值，但一阶颤振失稳临界流速值随着黏性系数的增大而增大，而二阶发散失稳临界流速值随着黏性系数的增大而减小。对同一黏性系数的变截面梁，随着厚度比的减小，一阶失稳临界流速值也在减小。

参 考 文 献

[1] Mote C D. A study of band saw vibration[J]．Journal of the Franklin Institute，1965，279(6)：430-444.

[2] Mote C D. On the non-linear oscillation of an axially moving string[J]．Journal of Applied Mechanics，1966，33(2)：463-464.

[3] Mote C D. Dynamic stability of axially moving materials[J]．Shock and Vibration Digest，1972，4(4)：2-11.

[4] Chen L Q, Yang X D. Vibration and stability of an axially moving viscoelastic beam with hybrid supports[J]. European Journal of Mechanics A/Solids, 2006, 25(6): 996-1008.

[5] Yang X D, Chen L Q. Non-linear forced vibration of axially moving viscoelastic beams[J]. Acta Mechanic Solida Sinica, 2006, 19(4): 365-373.

[6] Lee U, Kim J, Oh H. Spectral analysis for the transverse vibration of an axially moving Timoshenko beam[J]. Journal of Sound and Vibration, 2004, 271(3/4/5): 685-703.

[7] 赵凤群，王忠民，陆小平. 轴向运动功能梯度Timoshenko梁的稳定性分析[J]. 振动与冲击，2014，33(2): 14-19.

ZHAO Feng-qun,WANG Zhong-min,LU Xiao-ping.Stability analysis of axially moving Timoshenko beam made of functionally graded material[J]. Journal of Vibration and Shock, 2014,33(2):14-19.

[8] Mergen H G, Marco A. Steady-state transverse response of an axially moving beam with time-dependent axial speed[J]. International Journal of Non-Linear Mechanics,2013,49:40-49.

[9] Mergen H G, Marco A. Nonlinear dynamics of axially moving viscoelastic beams over the buckled state[J]. Computers and Structures, 2012, 112/113:406-421.

[10] Caruntu D. On nonlinear vibration of non-uniform beam with rectangular cross-section and parabolic thickness variation[M]. Berlin:Springer, 2000:109-118.

[11] Mehmet C E, Metin A, Vedat T. Vibration of a variable cross-section beam [J]．Mechanics Research Communica-tions, 2007, 34(1): 78-84.

[12] 徐腾飞, 向天宇, 赵人达. 变截面Euler-Bernoulli 梁在轴力作用下固有振动的级数解[J]. 振动与冲击,2007,26(11): 99-101.

XU Teng-fei, XIANG Tian-yu, ZHAO Ren-da. Natural vibration series solution of variable cross-section Euler Bernoulli beam under the action of axial force[J]. Journal of Vibration and Shock, 2007,26(11): 99-101.

[13] Floater M S,Hormann K.Barycentric rational interpolation with no poles and high rates of approximation[J]. Numerische Mathematik, 2007, 107(2): 315-331.

[14] 王波, 陈立群. 微分求积法处理轴向变速黏弹性梁混杂边界条件[J]. 振动与冲击, 2012, 31(5): 87-91.

WANG Bo, CHEN Li-qun. Treating hybrid boundary condition of an axially accelerating viscoelastic beam via a differential quadrature scheme[J].Journal of Vibration and Shock,2012,31(5):87-91.

基金项目：陕西省教育厅科学研究计划(11JK0524);陕西省自然科学资金资助项目(2011JM1013)

收稿日期：2015-01-13修改稿收到日期：2015-08-04

通信作者赵凤群 女，硕士生导师，1963年2月生

中图分类号:O317

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.017

Vibration and stability analysis of axially moving viscoelastic beam with varying section

LI Cheng-cheng, ZHAO Feng-qun

(School of Sciences, Xi’an University of Technology, Xi’an 710054, China)

Abstract:The governing differential equation of an axially moving viscoelastic beam with varying section was derived according to the D’Alembert principle, and a numerical method by the name of local differential quadrature method based on gravity interpolation was provided. The characteristic equation of a simply supported viscoelastic beam with varying section was obtained and the first two orders non-dimensional complex frequencies of the beam changing along with the non-dimensional axial moving speed were calculated. The form of instability of the viscoelastic beam with trapezoid cross section and parabolic cross section under different axial moving speed was analyzed in detail and compared with that of a uniform beam. The effects of height ratio and viscoelastic coefficient on the dynamic stability of the beam were discussed.

Key words:variable cross-section beam; viscoelasticity; axially moving; stability; differential quadrature method; complex frequency

第一作者 李成澄 女，硕士生，1988年12月生