正交各向异性矩形薄板振动的一种半解析方法

王　淼， 陈永强， 李志敏

(1.上海交通大学 船舶海洋与建筑工程学院，上海　200240；2. 中国运载火箭技术研究院，北京　100076; 3.上海交通大学 机械与动力工程学院，上海　200240)



正交各向异性矩形薄板振动的一种半解析方法

王淼1， 陈永强2， 李志敏3

(1.上海交通大学 船舶海洋与建筑工程学院，上海200240；2. 中国运载火箭技术研究院，北京100076; 3.上海交通大学 机械与动力工程学院，上海200240)

摘要：使用半解析的多项康氏法分析对边简支、对边固定和对边固定-简支的正交各向异性矩形薄板振动问题。选择多个梁特征函数作为试函数，精确满足对边所有边界条件。通过Gakerkin积分将偏微分振动方程转化为常微分方程组并整理为状态方程形式。强迫满足另一对边的边界条件，获得频率方程，确定固有频率。文献结果比较不仅证实了该方法的有效性，而且揭示通过该方法获得的对边简支板的解是精确解。最后，研究了不同长宽比下试函数项数对无量纲固有频率的影响。

关键词：正交各向异性矩形薄板；多项康氏法；梁特征函数；正交性条件；半解析解

矩形薄板是土木、航空航天等常用的结构形式，其振动一直受到广泛关注。对于经典的固定、简支和自由边界条件，矩形板总共有21种边界条件组合。其中，对边简支的6种边界组合存在精确解；其它的15种边界组合，受限于偏微分方程的内部耦合，通常认为精确解不存在。多年来，国内外学者使用各种方法对非对边简支板展开研究，试图获得较好的振动解，这些方法主要有解析法(例如叠加法[1]和辛方法[2])、数值法(例如瑞利-里兹法[3]和有限元法)和半解析法(例如康氏法[4]和延展康氏法[5])。一般说来，解析法过程复杂但结果精确，数值法形式简单但计算工作量大，而半解析法可以在精度和计算量之间取得很好的平衡。

康氏法(Kantorovich Method)[4]将变量表示为一个方向上满足几何边界条件的试函数和另一方向未知函数的乘积，通过变分或Galerkin积分求未知函数的精确解。康氏法的计算精度通常高于瑞利-里兹法，缺点在于计算精度依赖试函数。为进一步提高计算精度，延展康氏法(Extended Kantorovich Method)[5]将康氏法中未知函数的精确解用作新的试函数，轮换变量，通过反复迭代求解。其优点在于初始试函数可选择随意，不需满足任何边界条件，因为迭代会强制满足边界条件。

目前，采用单个试函数的康氏法和延展康氏法被用于矩形板的弯曲[6]、屈曲[7]和振动[8]等问题。以振动问题为例，Jones等[8]采用单项延展康氏法确定四边固定各向同性薄板的固有频率；Laura等[9]使用单项康氏法计算三边弹性支承一边自由的变厚度矩形薄板的基频；梁枢平[10]取梁挠函数为试函数，利用单项康氏法求解不同边界条件和长宽比下各项同性矩形薄板的固有频率；Bhat等[11]采用单项延展康氏法推导各向同性薄板的特征函数；Lee等[12]取单个Timoshenko梁函数为试函数，利用延展康氏法分析各向同性矩形厚板的振动特性；Sakata等[13]利用单项延展康氏法计算不同边界条件、材料模量比和长宽比下正交各向异性薄板的固有频率；Dalaei等[14]和Bercin[15]分别利用单项延展康氏法计算四边固定正交各向异性薄板的固有频率；Rajalingham等[16]利用单项延展康氏法确定四边固定各向同性薄板的特征函数；钟阳等[17]利用单项延展康氏法推导出弹性地基上四边自由矩形薄板振动的迭代表达式。

Yuan等指出，采用单项试函数，康氏法和延展康氏法的精度会受到限制，且不能求解剪切屈曲问题。但是，采用多项试函数会产生耦合微分方程组的求解困难问题，因此多项康氏法和多项延展康氏法在矩形板振动分析中应用很少。据作者所知，Ashour[18]采用多项康氏法研究对边简支和对边固定的单向厚度变化的正交各向异性矩形板振动问题；Shufrin等[19-20]以多项式幂级数为试函数，采用延展康氏法研究均匀中厚板以及双向厚度线性变化板的振动问题；Pairod等[21]同样以多项式幂级数为试函数，采用延展康氏法计算正交各向异性阶梯矩形薄板的固有频率。

本文选择梁特征函数作为试函数，使用多项康氏法分析对边简支、对边固定和对边固定-简支的正交各向异性矩形薄板的自由振动。利用梁特征函数的正交性，对位移和内力作正交分解，引入状态向量，通过传递矩阵法求解耦合微分方程组。在此基础上，计算了15种边界组合下矩形薄板的前六阶无量纲固有频率，并分析了梁特征函数的数目对计算结果的影响。

1正交各向异性矩形薄板的振动微分方程与边界条件

正交各向异性矩形薄板的振动微分方程可表达如下

(1)

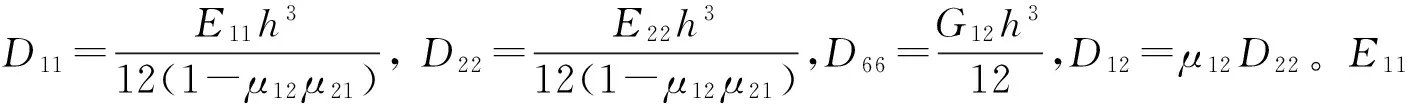
在x=0和x=a处的边界条件可表达为

(2)

而y=0和y=b处的边界条件可表达为

(3)

式中下标,x和,y分别代表对x和y的一阶偏导数。a和b分别为板的长度和宽度。Vx(x,y,t)，Mx(x,y,t)，Vy(x,y,t)和My(x,y,t)为内力分量，且

(4)

2特定边界条件下正交各向异性矩形薄板的半解析解

假设振动为简谐振动，那么

(5)

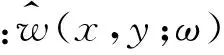
将式(5)代入式(1)可得

(6)

借助康氏法[18]，频域位移可表示为以下无限级数形式

(7)

式中:Yr(y)为y方向的试函数，而Wr(x;ω)为x方向的未知函数。在本文中，试函数取为欧拉-伯努利梁的特征函数，原因在于：对于对边简支、对边固定以及一边固定一边简支这些特定边界组合，梁特征函数能同时精确满足y=0和y=b处的板的几何和自然边界条件。

梁特征函数满足振动方程如下[22]

(8)

式中:βk代表梁的频率参数。对边简支、对边固定以及一边固定一边简支的梁特征函数表达、频率特征方程和频率参数见文献[3]。

梁特征函数还满足正交性条件如下[22]

(9)

式中：b代表梁长，即板宽。

将式(7)代入式(6)可得

D22WrYr,yyyy-ρhω2WrYr]=0

(10)

将式(18)乘以Yk(y)，对y在(0,b)范围内积分，应用正交性条件式(9)并整理可得

(D22Pk-ρhω2)Wk=0(k=1,2…∞)

(11)

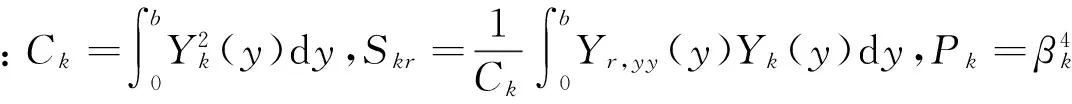
将式(5)和式(7)代入式(4)可得

(12)

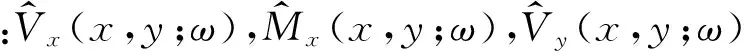
对式(12)中的第一式和第二式乘以Yk(y)，对y积分并应用正交性条件可得

仅取前N项梁特征函数作为试函数。相应地，式(11)整理为矩形形式如下

D11W,xxxx+2(D12+2D66)SW,xx+

(D22P-ρhω2I)W=0

(14)

式中：W={W1(x;ω),…,WN(x;ω)}T。S=[Skr],(k,r=1,2,…,N)， P=diag(P1,…,PN)。 I 和 0 分别为N×N的单位对角阵和N×1的零矩阵。

此外，式(13)整理为矩形形式如下

(15)

式中：V(x;ω)={V1(x;ω),…,VN(x;ω)}T，M(x;ω)={M1(x;ω),…,MN(x;ω)}T。

Z,x(x;ω)=A(ω)Z(x;ω)

(16)

式中

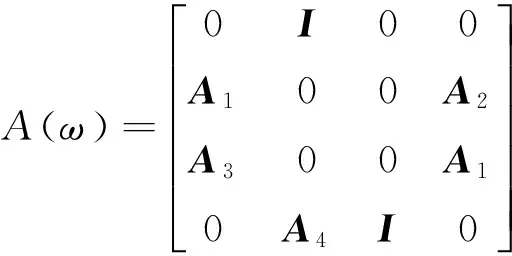
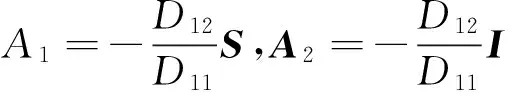
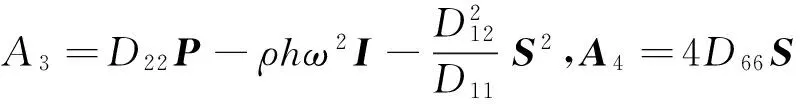
由式(16)，状态向量Z(0;ω)和Z(a;ω)的关系如下

Z(a;ω)=eA(ω)aZ(0;ω)

(17)

式中：eA(ω)a即为传递矩阵，它是一个8×8的分块矩阵。

由式(2)和式(15)可得，x=0和x=a处板的边界条件为

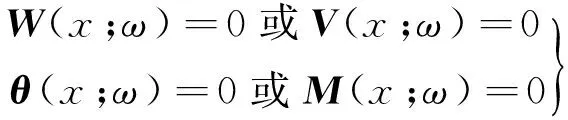
(18)

将板的边界条件式(18)代入式(17)，容易获得关于频率特征方程。考虑到频率特征方程为超越方程，可借助Newton-Raphson算法确定各阶固有频率。

3数值算例分析

表2将15种不同边界条件下各向同性方板的前六阶无量纲固有频率与文献[23]进行了比较。文献[23]使用Levy法确定对边简支板的固有频率，使用36项梁特征函数组合的瑞利-里兹法计算其它边界条件板的固有频率。在本文计算时，如无特别说明，取梁函数项数为6。比较发现，本文结果与文献结果吻合得非常好。尤其需要说明的是，对边简支情况下，本文结果与Levy法的结果完全相同，意味着使用S-S梁特征函数的多项康氏法获得的对边简支板固有频率是精确解。

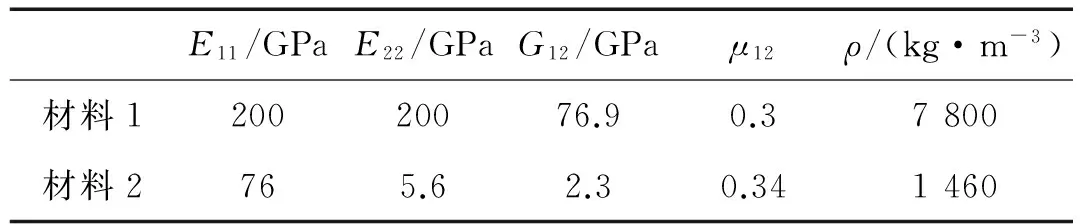
表1　材料参数

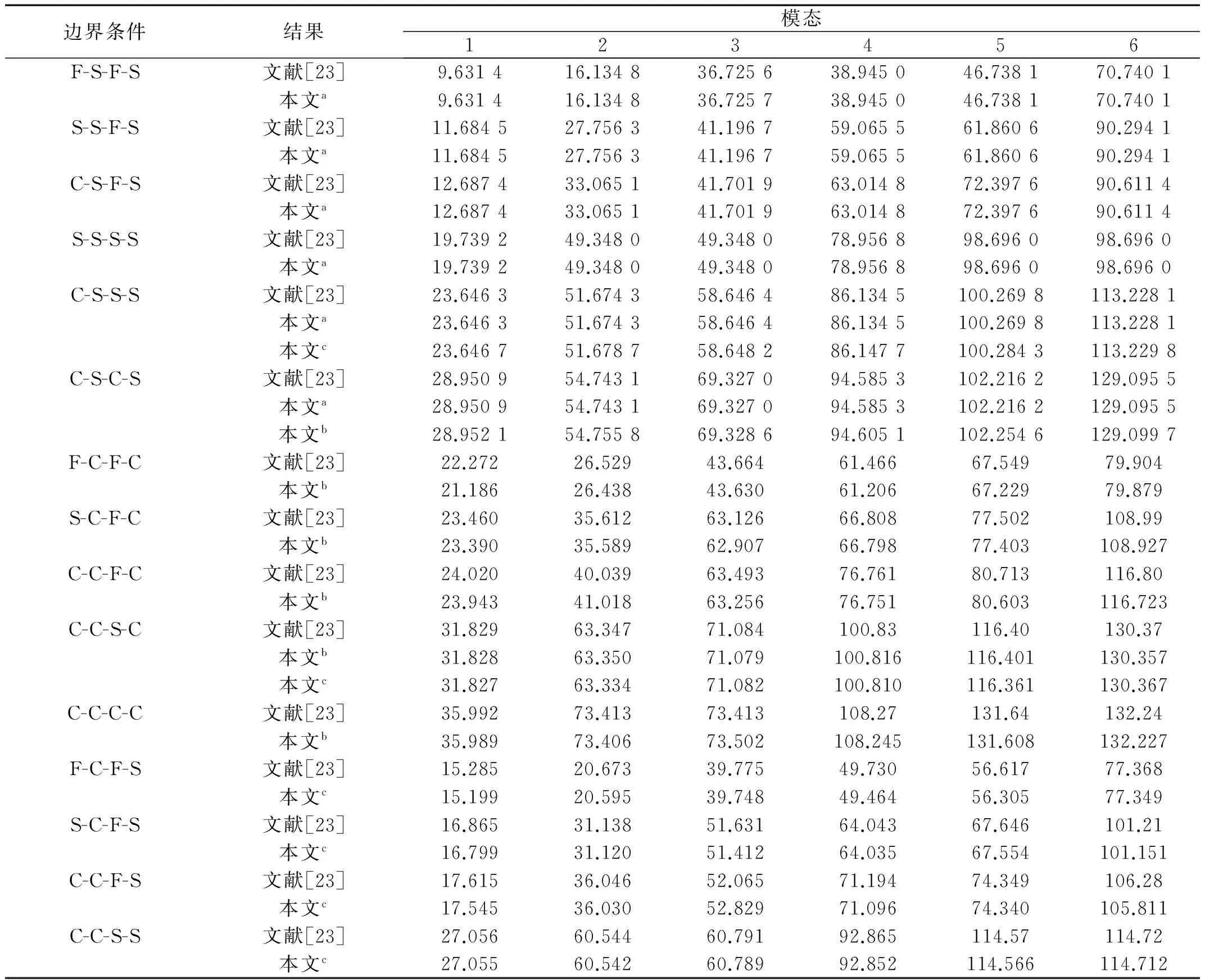
表2　不同边界条件的各项同性方板的无量纲频率(材料1)

注：a使用S-S梁函数；b使用C-C梁函数；c使用C-S梁函数。

为研究长宽比和梁函数项数对正交各向异性S-C-S-C板和S-C-S-S板的前六阶无量纲固有频率影响：表3将长宽比分别为1.0和2.0，梁函数项数分别为1～6时使用C-C梁函数获得的S-C-S-C板无量纲频率与精确解进行了比较；表4将长宽比分别为1.0和2.0，梁函数项数分别为1～6时使用C-S梁函数获得的S-C-S-S板无量纲频率与精确解进行了比较。其中，S-C-S-C板和S-C-S-S板的精确解分别由使用S-S梁特征函数的多项康氏法获得。比较发现：梁函数项数取1，即可获得非常高精度的基频；梁函数项数取为1～3时，会出现“漏频”现象；随梁函数项数的增加，使用C-C梁函数和C-S梁函数的多项康氏法求解结果不断从上逼近精确解；梁函数项数取6时，使用C-C梁函数和C-S梁函数的多项康氏法求解结果几乎与精确解完全相同。

表3　截断项取值对正交各向异性S-C-S-C板的无量纲频率的影响(材料2)

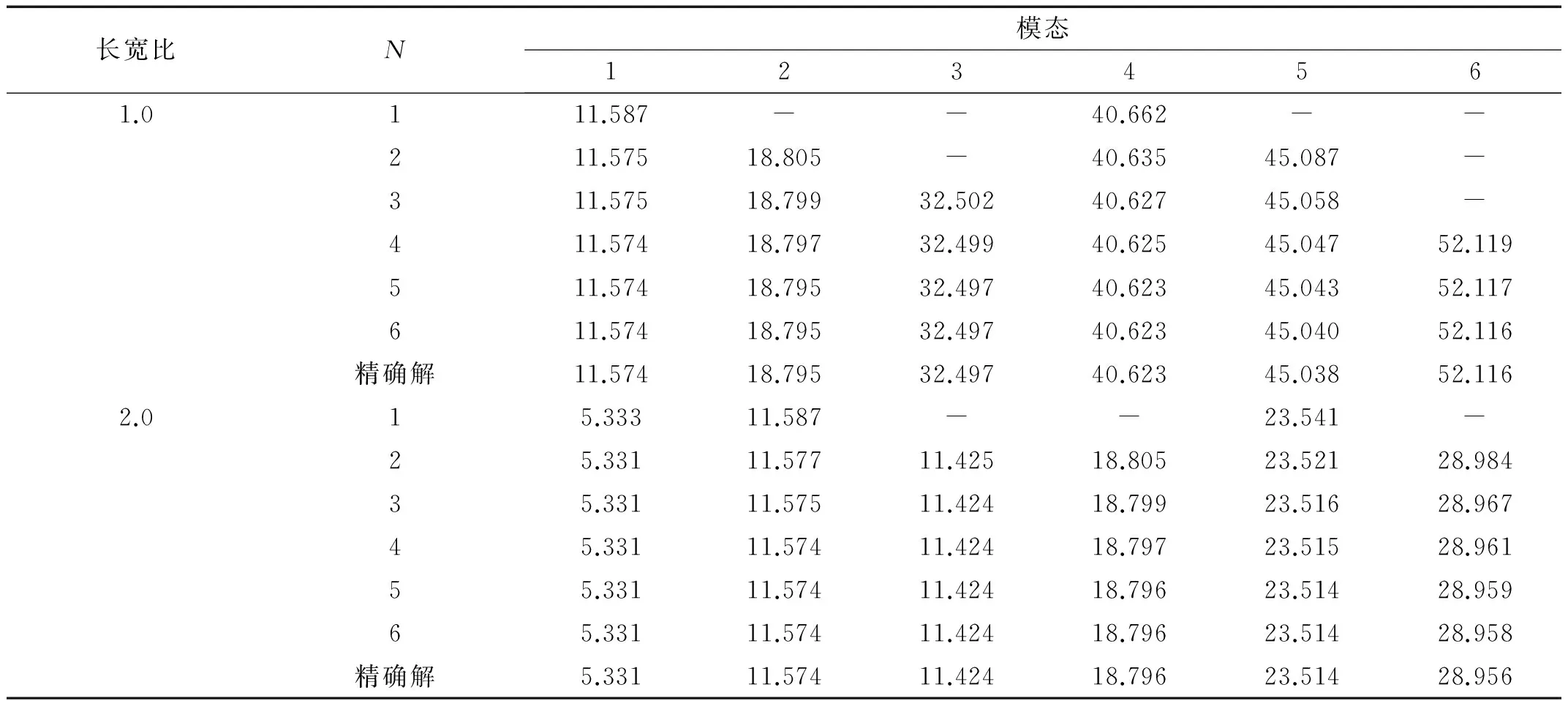
表4　截断项取值对正交各向异性S-C-S-S板的无量纲频率的影响(材料2)

4结论

针对对边简支、对边固定和对边固定-简支的正交各向异性矩形薄板振动问题，本文提出一种半解析方法，即多项康氏法。该方法使用梁特征函数为试函数，严格满足一对对边的所有边界条件。在此基础上，通过Galerkin积分将偏微分振动方程转化为常微分方程组。对位移和内力进行正交分解，借助传递矩阵和边界条件获得频率方程，确定固有频率。研究表明：对于对边简支的矩形薄板，由本文方法可获得精确解；对于对边固定和对边固定-简支的矩形薄板，依据本文方法可获得高精度的半解析解。考虑到振动微分方程和边界条件的相似性，该方法不仅仅适用于各项同性和正交各向异性矩形薄板的振动分析，而且可扩展用于交叉叠层复合材料矩形薄板。

参 考 文 献

[1] Gorman D J. Free vibration analysis of rectangular plates [M]. New York: Elsevier North Holland Inc, 1982.

[2] 钟阳, 张永山. 弹性地基上四边自由矩形薄板的解析解[J]. 应用数学和力学, 2006, 27(6): 735-740.

ZHONG Yang, ZHANG Yong-shan. Theoretic solution of rectangular thin plate on foundation with four edges free by symplectic geometry method [J]. Applied Mathematics and Mechanics, 2006, 27(6): 735-740.

[3] Leissa A W. Vibration of plates [R]. NASA SP-160. Washington DC: US Government Office, 1969.

[4] Kantorovich L V, Krylov V I. Approximate methods of higher analysis [M]. New York: Interscience Publisher, 1958.

[5] Kerr A D. An extended Kantorovich method for the stress analysis of a clamped rectangular plate[J]. Acta Mechanica, 1968, 6(2):180-186.

[6] Yuan S, Jin Y, Williams F W. Bending analysis of Mindlin plates by the extended Kantorovich method [J]. ASCE Journal of Engineering Mechanics, 1998,124(12): 1339-1345.

[7] Yuan S, Jin Y. Computation of elastic buckling loads of rectangular thin plates using the extended Kantorovich method [J]. Computers and Structures, 1998, 66(6): 861-867.

[8] Jones R, Milne B J.Application of the extended Kantorovich method to the vibration of clamped rectangular plates [J]. Journal of Sound and Vibration, 1976, 45(3): 309-316.

[9] Laura P A A, Grossi R O, Soni S R.Free vibrations of a rectangular plate of variable thickness elastically restrained against rotation along three edges and free on the fourth edge [J]. Journal of Sound and Vibration, 1979, 62(4): 493-503.

[10] 梁枢平. 求矩形薄板自振频率的一种近似解[J].振动与冲击, 1990, 9(4): 35-39.

LIANG Shu-ping. An approximate method for free vibration frequencies of rectangular thin plates [J]. Journal of Vibration and Shock, 1990, 9(4): 35-39.

[11] Bhat R B, Singh J, Mundkur G. Plate characteristic functions and natural frequencies of vibration of plates by iterative reduction of partial differential equation[J]. ASME Journal of Vibration and Acoustics, 1993,115(2):177-181.

[12] Lee J M, Kim K C.Vibration analysis of rectangular isotropic thick plates using Mindlin plate characteristic functions [J]. Journal of Sound and Vibration, 1995, 187(5): 865-867.

[13] Sakata T, Takahashi K, Bhat R B.Natural frequencies of orthotropic rectangular plates obtained by iterative reduction of the partial differential equation [J]. Journal of Sound and Vibration, 1996, 189(1): 89-101.

[14] Dalaei M, Kerr A D.Natural vibration analysis of clamped rectangular orthotropic plates [J]. Journal of Sound and Vibration, 1996, 189(3): 399-406.

[15] Bercin A N. Free vibration solution for clamped orthotropic plates using the Kantorovich method [J]. Journal of Sound and Vibration, 1996, 196(2): 243-247.

[16] Rajalingham C, Bhat R B, Xistris G D. Vibration of rectangular plates by reduction of the plate partial differential equation into simultaneous ordinary differential equations[J]. Journal of Sound and Vibration, 1997, 203(1): 169-180.

[17] 钟阳, 周福霖，张永山. 弹性地基上四边自由矩形薄板振动分析的Kantorovich法[J]. 振动与冲击, 2007, 26(3): 33-36.

ZHONG Yang, ZHOU Fu-lin,ZHANG Yong-shan. Vibration analysis of a thin plate on Winkler foundation with completely free boundary by Kantorovich method [J]. Journal of Vibration and Shock, 2007, 26(3): 33-36.

[18] Ashour A S. A semi-analytical solution of the flexural vibration of orthotropic plates of variable thickness [J]. Journal of Sound and Vibration, 2001, 240(3): 431-445.

[19] Shufrin I, Eisenberger M. Stability and vibration of shear deformable plates—first-order and higher-order analyses [J]. International Journal of Solids and Structures, 2005, 42(3/4): 1225-1251.

[20] Shufrin I, Eisenberger M. Vibration of shear deformable plates with variable thickness—first-order and higher-order analyses [J].Journal of Sound and Vibration, 2006, 290(1/2): 465-489.

[21] Pairod S, Parunya T.Vibration analysis of stepped rectangular plates using the extended Kantorovich method[J]. Mechanics of Advanced Materials and Structures, 2016,23(2):201-215.

[22] Leissa A W, Qatu M S. Vibration of continuous systems [M]. New York: McGraw-Hill, 2011.

[23] Leissa A W. The free vibration of rectangular plates [J]. Journal of Sound and Vibration, 1973, 31(3): 257-293.

基金项目：国家自然科学基金(10802047;51279222)；国家留学基金(201206235020)

收稿日期：2015-05-25修改稿收到日期：2015-09-29

通信作者李志敏 男，博士，副研究员，1974年9月生

中图分类号:TU33

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.14.003

Semi-analytical approach for the vibration analysis of orthotropic thin rectangular plates

WANG Miao1, CHEN Yong-qiang2, LI Zhi-min3

(1.School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240,China;2.China Academy of Launch Vehicle Technology, Beijing 100076,China;3.School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

Abstract:The semi-analytical multi-term Kantorovich method (MTKM) was adopted for the vibration analysis of orthotropic thin rectangular plates with two opposite edges both simply-supported, both clamped and one clamped the other simply-supported. Multiple beam characteristic functions were used as trial functions, which can satisfy the boundary conditions on two opposite edges exactly. With the Galerkin integral, the partial differential equation of motion was turned into several ordinary differential equations, which were then rewritten in the form of a space-state equation. Being enforced to satisfy the boundary conditions on the other two opposite edges, the transcendent frequency equation was derived and the non-dimensional frequencies were determined. Good agreements are shown between the present results and those from the references. It is revealed that the results from present method are exact for thin plates with two opposite edges both simply-supported. Moreover, the effect of the term number of trail functions on the non-dimensional frequencies under different aspect ratios was also investigated.

Key words:orthotropic thin rectangular plate; multi-term Kantorovich method; beam characteristic function; orthogonal condition; semi-analytical solution

第一作者 王淼 男，博士，助理研究员，1978年9月生

E-mail：zmli@sjtu.edu.cn