中空轴系多模态纵向减振研究

赵　帅， 陈　前， 黄志伟， 姚　冰

(1.南京航空航天大学 机械结构力学及控制国家重点实验室, 南京　210016；2.中国舰船研究设计中心，武汉　430064)

中空轴系多模态纵向减振研究

赵帅1， 陈前1， 黄志伟2， 姚冰1

(1.南京航空航天大学 机械结构力学及控制国家重点实验室, 南京210016；2.中国舰船研究设计中心，武汉430064)

采用阻尼动力吸振器对中空轴系纵向多阶模态进行振动控制，结合子结构综合法和传递矩阵法，建立了多个阻尼动力吸振器-轴系耦合系统的动力学模型，并进行了动力学特性分析。考虑到各阶阻尼动力吸振器间的相互影响，以极小化目标频段范围内轴系位移响应的均方值为目标函数，对各阶阻尼动力吸振器的参数进行了联合优化;针对轴系中空特点，设计了阻尼动力吸振器的具体结构形式，利用有限元仿真对理论计算进行了验证。研究表明：轴系多模态控制时，在多阶阻尼动力吸振器作用下，目标频段范围内的轴系纵向共振峰得到抑制，频响曲线趋于平缓；对多阶吸振器进行联合优化后，吸振器的吸振效果得到进一步提升；提出的多阶吸振器设计方法能为连续系统多模态振动控制提供参考。

中空轴系；纵向振动；传递矩阵法；阻尼动力吸振器

随着船舶动力系统的功率越来越大，推进轴系的纵向振动固有频率也随之越来越低，螺旋桨在船体尾部产生的不均匀伴流会使船舶推进轴系产生纵向共振。推进轴系的纵向振动不仅影响到推进轴系的工作寿命，而且会影响到船员的作息生活。对于军事舰艇来说，推进轴系振动还会通过轴承基座传递到船体，引起船体的振动，进而在船体周围形成辐射声场，严重影响舰艇的声隐身性。

动力吸振器结构简单，减振效果好，可以作为船舶推进轴系纵向振动控制的有效手段[1]。利用动力吸振器减振的措施是在推进轴系上添加一个子结构，通过优化设计子结构的参数可以显著减小轴系特定频段上的振动响应[2]。Goodwin[3]率先提出采用共振转换器调谐吸振来减小推进轴系的纵向振动，不过其需要安装在轴系和推力轴承之间，而且具体结构形式还尚未真正形成。Dylejko等[4-7]在Goodwin基础上，对共振转换器的结构参数进行了优化，并研究了其对推进轴系纵振引起的水下辐射噪声的控制效果。近年来，国内一些学者也开始了利用共振转换器进行轴系纵向减振的研究。刘耀宗等[8]用功率流法分析了推进轴系纵振传递到船体的能量以及动力吸振器对纵向的减振效果，分析表明纵向动力吸振器能够有效地衰减一定频率范围内的共振峰值。李良伟等[9]采用优化算法得到了吸振器参数的最优值。

事实上，随着船舶推进轴系结构的大型化，利用吸振器对轴系的一阶纵振模态进行控制已逐渐不能满足轴系减振要求。所以针对船舶推进轴系多模态纵向振动控制的研究显得很有必要。目前，针对此方面的研究尚不多见。此外，上述的动力吸振器由于需要安装在推力轴承基座上，对结构变动较大。实际上，由于中空轴在保证结构强度的前提下能大量减轻重量，早已广泛应用于船舶领域。基于这一特点，本文提出将吸振器安置在轴系空腔内，避免对轴系结构进行改动，可以作为船舶推进轴系振动控制的一种在工程上可行的方式。

本文针对中空轴系纵向振动多阶模态，采用阻尼动力吸振器对轴系进行纵向减振，运用子结构综合法以及传递矩阵法建立了附加多个阻尼动力吸振器的轴系动力学模型，结合轴系的中空特点，设计了阻尼吸振器的具体结构形式。考虑到各阶吸振器间的相互耦合，以轴系目标频段范围内的位移响应的均方值为目标函数，对吸振器的参数进行了联合优化，从而获得最优的减振效果。

1附加多个阻尼动力吸振器轴系的动力学模型

在研究阻尼动力吸振器的减振效果时，需要对主振系-吸振器系统进行动力学建模，通常将主振系简化为单自由度系统，但对于连续弹性体的推进轴系而言，为了计算出更接近实际情况的减振效果，不能简单地将主振系简化为单自由度系统。而且采用多个吸振器对轴系多个模态进行振动控制时，要求对多个吸振器的总体减振效果进行综合评估，因此需要建立较复杂的轴系模型。

对于连续弹性体的轴系，一般都采用传递矩阵法计算轴系的动力学响应，但对于局部含有多个并联结构的耦合系统则无法直接采用传递矩阵法进行响应计算。本文结合子结构综合法和传递矩阵法，将轴系离散成若干个轴段单元，把吸振器作为子结构，先将并联子结构的轴段单元化为二自由度系统单独考虑，得到子系统与其所依附的单元在对接点处的关系，再利用传递矩阵法得到含有子结构的轴段单元与余下各轴段单元之间的关系，进而建立子系统与轴系各个单元之间的联系。最后将子系统对轴系的作用等效为轴段单元在对接点处的外力，整个耦合系统进而等效为受到若干外力作用下的链式结构，再结合传递矩阵法计算耦合系统的动力学特性。

图1为并联多个阻尼动力吸振器轴系的复杂系统，轴系离散为p个轴段单元，吸振器的位置分别在第iP1,…,iPj,…,iPn个单元，数量为n。同时，轴系还在第t个轴段单元处受到简谐外力F0sinωt的作用。对于轴系主系统而言，吸振器质量块运动产生的反作用力会传递到轴系，相当于轴系在第iP1,…,iPj,…,iPn个单元处会产生附加的外激励力P1sin(ωt),…,Pjsin(ωt),…,Pnsin(ωt)，这些激励力方向与轴系在单元iP1,…,iPj,…,iPn处的运动方向相反，频率相同。故先将n个附加阻尼动力吸振器的轴段单元单独考虑，根据基础简谐激励受迫振动理论，对接点处各吸振器产生的作用反力Pk可表示为：

Pk=Dk(ω)AiPk

(1)

图1　附加多个阻尼吸振器轴系的简化模型Fig.1 Simplified model of a shafting with multiple damped DVAs

对于单元iPj处的第j个吸振器而言，其对接点处的基础位移与外激励力和n个吸振器产生的对接力有关，即

(2)

式中：uiPj,F0为外力F0作用下单元iPj处所产生的位移；uiPj,Pk为对接力Pk作用下单元iPj处所产生的位移。求解uiPj,Pk需要得到n个对接力Pk(k=1,2,…,n)，而由式(1)知Pk为AiPk的函数，从而需要经过推导得到对接力Pk的表达式。

对于轴系纵向振动，定义各轴段单元的状态矢量为z=[X,N,1]T，式中X,N分别表示位移和力。假设仅在第iPj个单元的对接点处施加单位力，该单元的传递矩阵则表示为

UPj,iPj=

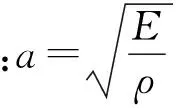
此时，余下的p-1个单元的传递矩阵表示为

(k=1,2,…,iPj-1,iPj+1,…,p)

(4)

同样，仅当第t个单元上受到外力F0作用时，该单元的传递矩阵表示为

(5)

此时，余下p-1单元的传递矩阵可以表示为

(k=1,2,…,t-1,t+1,…,p)

(6)

为了简化后续的推导，令

(7)

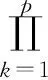
(k=1,2,…,p)

(8)

从而根据式(3)和式(4)可以得到，仅在轴系第iPj个单元施加单位力时，轴系总传递矩阵为

(9)

同样，根据式(5)和式(6)可知，仅在轴系第t个单元施加外力F0时，轴系总传递矩阵为

(10)

再令

(k=1,2,…,iPj)

(11)

根据传递矩阵关系可得，当轴系仅在第iPj个单元受到对接力Pj作用时，使得第iPj个单元对接点处产生的位移为

(12)

同样，当轴系仅在第t个单元受到外力F0作用时，使得第iPj个单元对接点处产生的位移为

(13)

将式(12)和(13)代入式(2)可知第j个吸振器的对接点处的纵向位移幅值为

等式两边同乘以Dk，并将n个对接力展开成矩阵形式，则得到

(15)

令

(16)

(17)

(18)

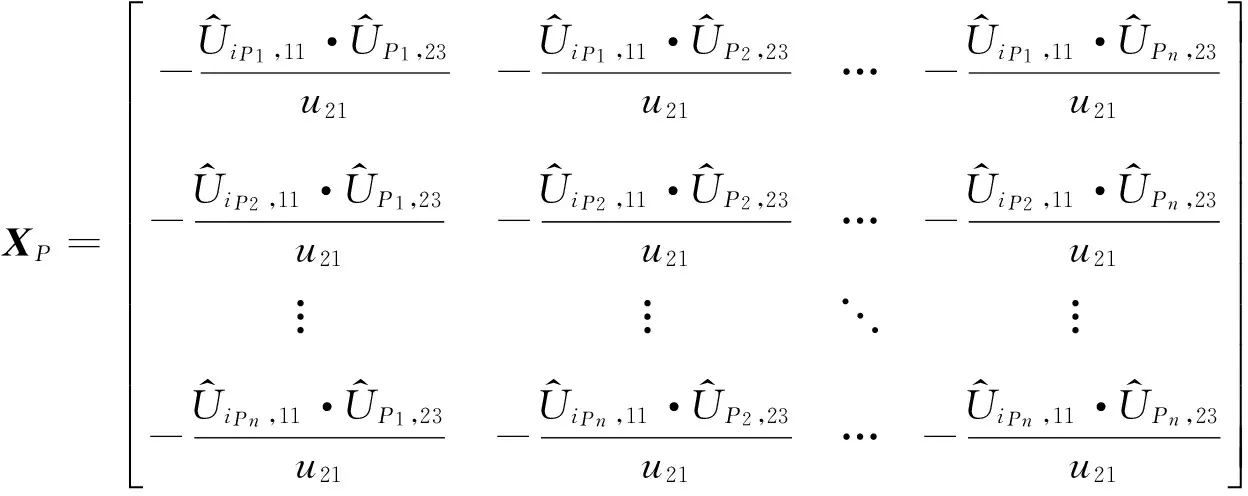
此时，式(15)可表示为

P=D[XPP-XF]

(20)

从而得到

P=[XP-D-1]-1XF

(21)

至此，可得到n个吸振器产生的对接力，进而可知轴系在iP1,…,iPj,…,iPn单元处受到n个对接力作用下的总传递矩阵表示为

(22)

其中第iP1,…,iPj,…,iPn个单元的传递矩阵表示为

UP,iPk=

(k=1,2,…,n)

(23)

余下p-n个单元的传递矩阵表示为

(k=1,2,…,p且k≠iP1,iP2,…,iPn)

(24)

根据式(22)可得轴系在n个吸振器的作用下任意单元位置处的位移，再通过式(10)可得轴系在外力作用下任意单元位置处的位移，根据叠加原理，可以得到轴系在n个阻尼动力吸振器和外力共同作用下任意位置处的响应。对于两端自由的边界条件，即X0≠0，N0=0，Xp≠0，Np=0，可求得轴系左端点的位移响应为:

(25)

轴系右端点的位移响应为

Xn=xF0,n-xP,n=

(26)

2吸振器设计

对于图2所示的两端自由的船舶推进轴系，轴段材料为45号钢，密度为7 850 kg/m3，各轴段具体尺寸见图2。针对推进轴系的前三阶纵振模态，在轴系内部空间分别布置三个阻尼动力吸振器对其进行纵向减振。

图2　推进轴系尺寸参数Fig.2 Parameters of the shafting

2.1吸振器结构形式

考虑到轴系的中空特点，吸振器设计见图3,其由芯棒和黏弹性材料组成。吸振器的质量由芯棒提供，芯棒材料为45号钢。黏弹性材料提供吸振器所需的刚度和阻尼。图3中R1和R2分别为芯棒和黏弹性材料的外半径，l为黏弹性材料长度。

图3　吸振器结构示意图Fig.3 Schematic diagram of the DVA

对于圆柱形黏弹性材料，其受到剪切力时的纵向刚度可近似表示为[10]

(27)

式中：G为黏弹性材料的剪切模量，R1、R2和l分别为圆柱形黏弹性材料的内、外半径和长度。

2.2吸振器参数设计

根据轴系纵向振动前三阶振型(见图4)可知，前三阶阻尼动力吸振器均可安放在轴系左端部。吸振器安装顺序从左到右依次为三阶、二阶和一阶，从而尽可

能地避开各阶节点。

对各阶阻尼动力吸振器进行设计时，需要将轴系等效为各阶纵振频率下的单自由度系统，从而获得轴系在吸振器各安装位置处的等效质量。根据等效原理可以得到轴系的前三阶纵振等效质量，并设定各阶阻尼动力吸振器的质量比u，具体参数见表1。根据吸振器最佳调谐频率比

(28)

可得各阶吸振器的固有频率f，再结合吸振器的最优阻尼比

(29)

图4　轴系前三阶纵振振型Fig.4 First three modes of longitudinal vibration of the shafting

求得各阶吸振器的阻尼，综上可得各阶吸振器的参数，见表2。

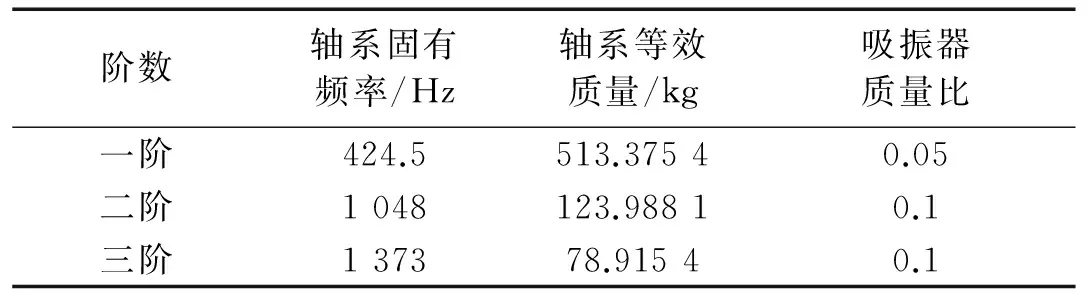
表1　吸振器质量比

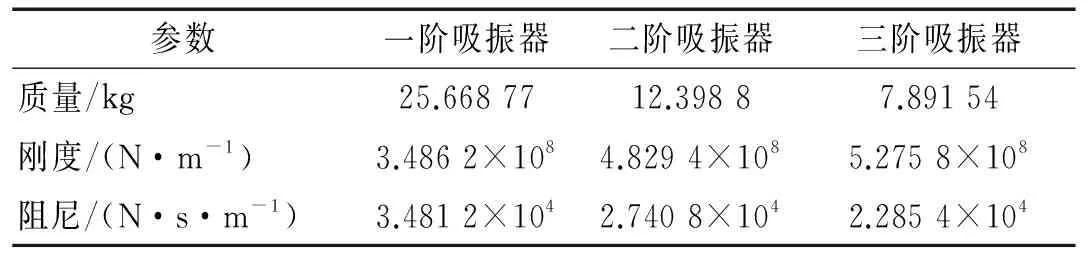
表2　吸振器参数

2.3吸振器参数优化

对于附加多个吸振器的轴系，各阶动力吸振器之间会相互影响，对于单个吸振器的优化设计方法不能完全适用于多吸振器的优化设计，为了达到最优的减振效果，有必要对各阶吸振器的参数进行整体的优化设计。

2.3.1优化方法

由于各阶动力吸振器的质量已经确定，将吸振器的刚度和阻尼作为设计变量，优化选用的目标函数为极小化目标频段范围内系统位移响应的均方值y：

(30)

式中：ω1为目标频段的起始角频率，ω2为终止角频率，X(ω)为位移响应。

对于多阶阻尼动力吸振器的优化属于多变量、非线性约束最优化问题，针对这一问题的求解方法有很多，本文采用Matlab工具箱中提供的fimncon求解函数。

2.3.2优化结果

由于本文考察多阶纵向振动的宽频减振效果，故选取极小化300～1 700 Hz范围内轴系右端点的均方响应为目标函数对各阶吸振器的刚度和阻尼进行联合优化，优化后的结果见表3。表4给出了吸振器联合优化前后轴系右端点的位移插入损失，结果表明吸振器联合优化后插入损失进一步增大。

表3　优化后吸振器参数

表4　优化后插入损失

3减振效果分析

根据联合优化后的吸振器参数，可以计算得到附加三个阻尼动力吸振器后轴系的动力学响应，计算时，在轴系的最右端施加单位纵向激励力。图5为吸振器加入前后轴系右端点的位移频响函数曲线，从图5可知,阻尼动力吸振器加入前的轴系在前三阶纵向共振频率(424.5 Hz，1 048 Hz，1 373 Hz)处出现很尖锐的共振峰。在加入三个吸振器后，轴系的前三阶纵向共振峰均得到抑制，频响函数曲线趋于平缓，结果表明所设计的前三阶阻尼动力吸振器对轴系纵向振动具有明显的减振效果。

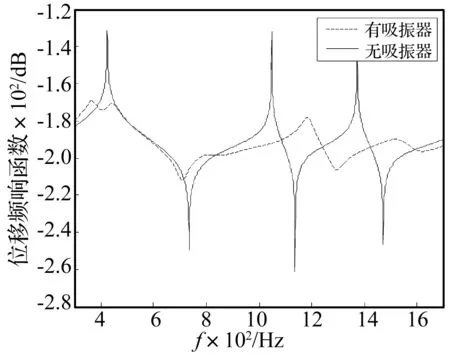
图5　吸振器加入前后轴系右端点的位移频响曲线Fig.5 Calculated results of FRF of displacement of the shafting

为了验证理论计算结果，利用有限元软件对附加阻尼动力吸振器的轴系进行仿真计算，有限元仿真计算时吸振器的建模采用实体单元建模，根据优化参数所确定的吸振器的具体结构参数见表5。将有限元软件仿真结果同传递矩阵法计算结果进行对比，结果见图6，从图6可知,理论和仿真结果吻合良好，只是共振峰大小有些差异，但对应的频率基本没有偏差，从而也进一步验证了理论建模的准确性。值得说明的是，对于轴系这样的大型结构而言，传递矩阵法计算相比于有限元软件仿真可以节省大量的时间。

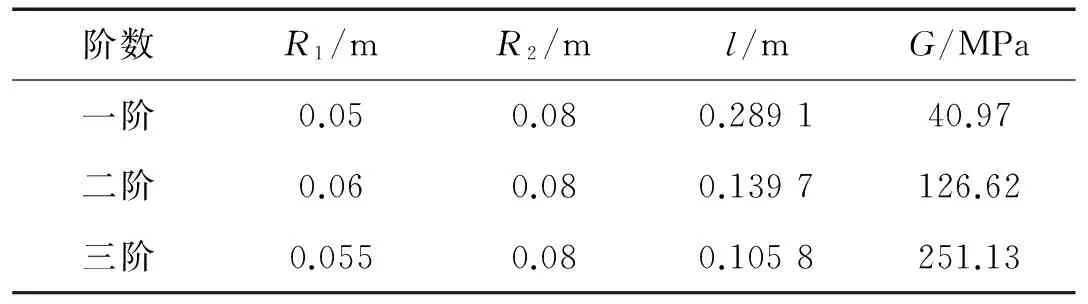
表5　吸振器结构参数

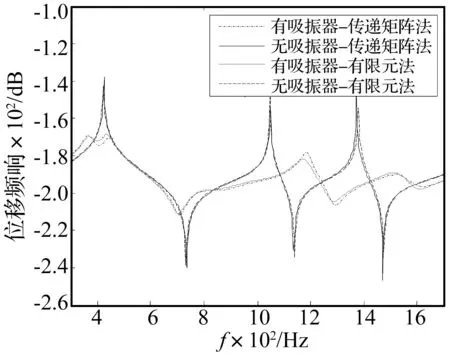
图6　理论计算与仿真结果对比Fig.6 Comparison between calculated and stimulated results of FRF of displacement of the shafting

4结论

(1) 对于附加多个阻尼动力吸振器轴系的耦合系统，将各个阻尼动力吸振器对轴系的作用等效成反作用力，进而结合子结构综合法和传递矩阵法得到系统的动力学特性，此方法可以作为连续系统吸振器设计的一种参考方法。

(2) 采用多阶吸振器对轴系进行多模态振动控制时，各阶吸振器之间会通过轴系相互影响，不能孤立地进行各阶吸振器的设计，需要对各阶吸振器进行整体优化，进而获得最优的减振效果。

(3) 轴系加入多阶阻尼动力吸振器后，理论和仿真结果都表明轴系的纵向共振峰得到抑制，能够在相当宽的频带范围内衰减振动，减振效果非常明显。考虑到大型船舶推进轴系的中空特点，本文采用的芯棒式阻尼动力吸振器，能在不增加安装空间的前提下，拥有好的减振效果，具有一定的工程应用前景。

[1] 杨志荣，秦春云，饶柱石，等.船舶推进轴系纵振动力吸振器设计及参数影响规律研究[J].振动与冲击, 2012,31(16):48-51．

YANG Zhi-rong,QIN Chun-yun,RAO Zhu-shi,et al.Design and analysis of a dynamic absorber for reducing axial vibration of ship shafting [J].Journal of Vibration and Shock,2012,31(16):48-51．

[2] 刘耀宗,郁殿龙,赵宏刚,等.被动式动力吸振技术研究进展[J].机械工程学报, 2007, 43(3): 14-21.

LIU Yao-zong，YU Dian-long，ZHAO Hong-gang，et al.Review of passive dynamic vibration absorbers[J]. Chinese Journal of Mechanical Engineering, 2007, 43(3): 14-21.

[3] Goodwin A J H.The design of a resonance changer to overcome excessive axial vibration of propeller shafting[J].Institute of Marine Engineers Transactions,1960,72:37-63．

[4] Dylejko P G,Kessissoglou N.Minimization of the vibration transmission through the propeller-shafting system in a submarine[J].Journal of the Acoustical Society of America,2004,116(4):25-69．

[5] Dylejko P G,Kessissoglou N,Tso Y,et al.Optimization of a resonance changer to minimize the vibration transmission in marine vessels[J].Journal of Sound and Vibration,2007,300:101-116．

[6] Dylejko P G.Optimum resonance changer for submerged vessel signature reduction[D].Sydney:University of New South Wales,2007．

[7] Merz S, Kessissoglou N,Kinns R,et al.Minimization of the sound power radiated by a submarine through optimization of its resonance changer[J].Journal of Sound and Vibration,2010,329:980-993．

[8] 刘耀宗,王宁,孟浩,等.基于动力吸振器的潜艇推进轴系轴向减振研究[J].振动与冲击, 2009,28(5):184-187.

LIU Yao-zong, WANG Ning, MENG Hao，et al.Design of dynamic vibration absorbers to reduce axial vibration of propelling shafts of submarines[J]. Journal of Vibration and Shock,2009,28(5):184-187．

[9] 李良伟,赵耀,陆坡,等.减小船舶轴系纵向振动的动力减振器参数优化[J].中国造船,2010,51(2):139-148．

LI Liang-wei,ZHAO Yao,LU Po，et al.Optimization of dynamic absorber parameters for reducing axial vibration of ship shafting[J]. Shipbuilding of China,2010,51(2):139-148．

[10] Ernst F G. Rubber Springs Design[M]. London: Newnes-Butterworths, Wiley, 1974.

Research on reduction of multi-mode longitudinal vibration of hollow shafting

ZHAO Shuai1， CHEN Qian1， HUANG Zhi-wei2， YAO Bing1

(1.State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China; 2. China Ship Development and Design Center, Wuhan 430064, China)

Damped dynamic vibration absorbers are adopted to attenuate the multi-mode longitudinal vibration of the hollow shafting. A dynamic model of the shafting with multiple dynamic vibration absorbers is established using the transfer matrix method combined with the substructure synthetic method. The dynamic behavior of the shafting under harmonic excitation is then analyzed. Considering the coupling behavior of the dynamic vibration absorbers, the parameters of the dynamic vibration absorbers are optimized, specifically relating to the mean square of the displacement response in a targeted frequency range as an object function. Based on the hollow characteristic of the shafting, a specific structure of the dynamic vibration absorber is designed, and finite element stimulation is used to verify the theoretical calculation. The research results showed that the resonance peak is strongly attenuated and that the frequency response function curve turned smooth when multiple dynamic vibration absorbers were attached to the shafting. Furthermore, the absorption effect is improved after an optimization of the dynamic vibration absorbers.

hollow shafting；longitudinal vibration；transfer matrix method; dynamic vibration absorber

10.13465/j.cnki.jvs.2016.12.015

江苏高校优势学科建设工程资助项目；中央高校基本科研业务费专项资金资助；江苏省普通高校研究生科研创新计划资助项目(KYLX_0242)

2015-05-20修改稿收到日期：2015-07-08

赵帅 男，博士生，1990年生

陈前 男，教授，博士生导师，1951年生

TB532

A