基于径向基函数的局部近似特解法求解二维薛定谔方程

洪永兴　陈　文　林　继

(河海大学 力学与材料学院， 南京　211100)



基于径向基函数的局部近似特解法求解二维薛定谔方程

洪永兴陈文林继

(河海大学 力学与材料学院， 南京211100)

摘要：基于径向基函数的局部近似特解法具有形式简单、易编程、精度高、收敛速度快等优点，是一种纯无网格配点方法．它通过将计算域划分为若干子区域并利用各个区域内的节点构造局部低阶矩阵，然后再将该矩阵拓展为全局形式，从而构造一个全局稀疏矩阵，以便于快速计算．本文采用局部近似特解法数值模拟二维薛定谔方程，首先采用隐式欧拉差分格式对时间项进行离散，并利用基于Multiquadric(MQ)函数的局部近似特解法对空间项进行离散．数值实验表明，局部近似特解法求解精度高、收敛速度快且计算耗时少，具有较好的工程应用前景．

关键词：隐式欧拉差分；二维薛定谔方程；Multiquadric函数；局部近似特解法；全局近似特解法

薛定谔方程是重要的波动方程之一，广泛存在于光学、生物学、海洋学等领域[1-3]．国内外许多学者对薛定谔方程进行了深入的研究[4-7]．但是因为薛定谔方程形式的复杂性，解析求解变得相当困难，所以寻找一个简单、快速、有效的数值方法具有重要的理论意义和应用价值．

径向基函数配点法作为一种重要的无网格方法，被广泛用于研究科学和工程问题[8-12]．该方法具有精度高，编程容易，思路简单等优点．但是，采用全局的径向基函数配点方法在求解过程中可能产生病态稠密矩阵，影响计算结果，并且计算耗时长阻碍了其在大规模科学和工程问题中的应用．为了克服该缺点，学者们提出了局部化的径向基函数方法，此类方法能快速高效地处理大规模科学和工程问题．目前，基于径向基函数的局部方法有以下几种：局部紧支径向基函数方法[13]、局部径向基函数配点法[14]、基于径向基函数的局部微分求积法[15]和局部近似特别解法[16]等．其中局部近似特别解法最早由Chen和Yao提出，用于心血管内钙元素动力学行为模拟[17]等大规模物理力学问题．随后局部近似特解法得到学者们的关注，被用于波和热传导问题的数值模拟[18-20]．

本文采用局部近似特解法数值模拟二维薛定谔方程，首先采用隐式欧拉差分法对时间项进行离散，然后采用基于MQ函数的局部近似特解法对空间项进行离散，从而离散整个薛定谔方程．通过与全局近似特解法进行系统的比较发现，局部近似特解法求解精度高、收敛速度快且计算耗时少．

1薛定谔方程及时间项离散

1.1二维薛定谔方程

本文考虑如下简单形式的二维薛定谔方程：

(1)

考虑如下初始条件和边界条件：

(2)

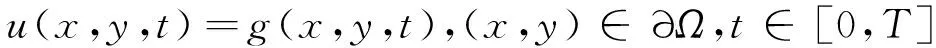
(3)

1.2时间项离散

首先采用隐式欧拉差分格式对式(1)时间项进行离散，可得

(4)

其中dt为时间步长dt=tn+1-tn，tn=n·dt，以及un=(x，y，tn)，Δun=∂2u(x，y，tn)/∂x2+∂2u(x，y，tn)/∂y2．

将包含un+1和un的项分别整理到等号的左边和右边，可得

(5)

2近似特解法与局部近似特解法

2.1近似特解法

不失一般性，考虑如下的偏微分方程：

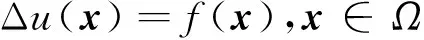
(6)

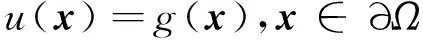
(7)

其中未知数x=(x1，x2)，u(x)为待求的函数，Ω为问题的求解区域，∂Ω为区域边界满足Dirichlet边界条件，f(x)和g(x)为已知函数．那么未知函数u(x)可以表示为径向基函数的线性组合，如下：

(8)

(9)

(10)

其中，φ=ΔΦ，ni为内部点数，nb=n-ni为边界点数，n为总点数．由此可以计算出式(8)的未知系数{αj}．

近似特解法和Kansa方法的主要区别在于：近似特解法是对径向基函数φ积分求得Φ的表达式，而Kansa方法是对Φ进行求导得到φ的具体表达式[21]．本文采用MQ函数作为径向基函数，分别采用特解法和Kansa方法推导得到如下Φ和φ：

Kansa方法：

特解法：

其中c为形状参数．需要指出的是，采用全局的近似特解法(Globalmethodofapproximateparticularsolution，GMAPS)将可能产生病态稠密矩阵，会增加计算耗时并影响计算精度，难以处理大规模科学和工程问题[8]．

2.2局部近似特解法

局部近似特解法(Localizedmethodofapproximateparticularsolution，LMAPS)可以从一定程度上减少病态稠密矩阵对结果的影响．它将全局空间划分成若干子区域，对每个区域利用径向基函数进行插值．一般构造影响区域的方式是以某一插值点为中心寻找该插值点邻近的ns个点作为它影响区域，称ns为区域值．下面简单介绍局部近似特解法的基本步骤，由式(8)可得

(11)

由式(9)～(11)可得

(12)

其中uhI=[f(x1) f(x2) … f(xni)]T，uhB=[g(xni+1) g(xni+2) … g(xn)]T，AI=[φij]ni×n，AB=[Φij]nb×n．那么

(13)

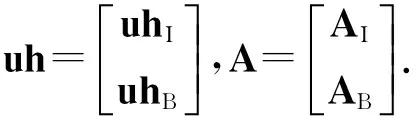
接着在每个子区域Ωc内，采用近似特解法构造低阶矩阵：

(14)

其中Ωc，Ac分别表示以xc为中心的影响区域和该区域的满秩矩阵．

由式(14)和(13)可得

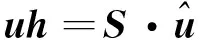
(15)

(16)

其中

此外局部近似特解法中的形状参数不是常数，而是与距离相关的变量

(17)

其中dr是区域中心点到各点的最大距离，c为常数．

3数值结果和讨论

本节采用局部近似特解法求解二维薛定谔方程．为了验证该方法的有效性，本文求解两种区域问题：规则和不规则区域．误差分析采用标准误差(Rootmeansquareerror， RMS)，相对误差(Relativeerror， RE)和最大相对误差(Maximumrelativeerror， MRE)，定义如下：

MRE=max(RE(xk))k=1，2，…，M

式中，M为测试点总数．其中RMSr表示实部标准误差，RMSi表示虚部标准误差，REr表示实部相对误差，REi表示虚部相对误差．

考虑如下二维薛定谔方程：

(18)

初始条件u(x，y，0)和边界条件u(x，y，t)分别为：

(19)

(20)

用于比较的解析解为：

(21)

3.1算例1：规则区域

首先考虑如图 1所示的规则区域，其中边界点数nb=108，内部点数ni=415，总点数n=523．

图1　规则区域及配点示意图

图2给出了局部近似特解法和全局近似特解法的误差，其中dt=0.01，ns=13，c=15(LMAPS)，c=0.1(GMAPS)．数值结果表明两者均能较好地模拟二维薛定谔方程，并且LMAPS方法的数值精度在某些时刻较GMAPS高．

由文献可知，局部近似特解法采用与节点距离有关的形状参数可以有效地降低形状参数c对精度的影响[20]．图3显示了误差与形状参数c之间的关系．从图3可以看出，局部近似特解法形状参数c的有效取值范围比全局近似特解法的大得多，该结果验证了上述结论．

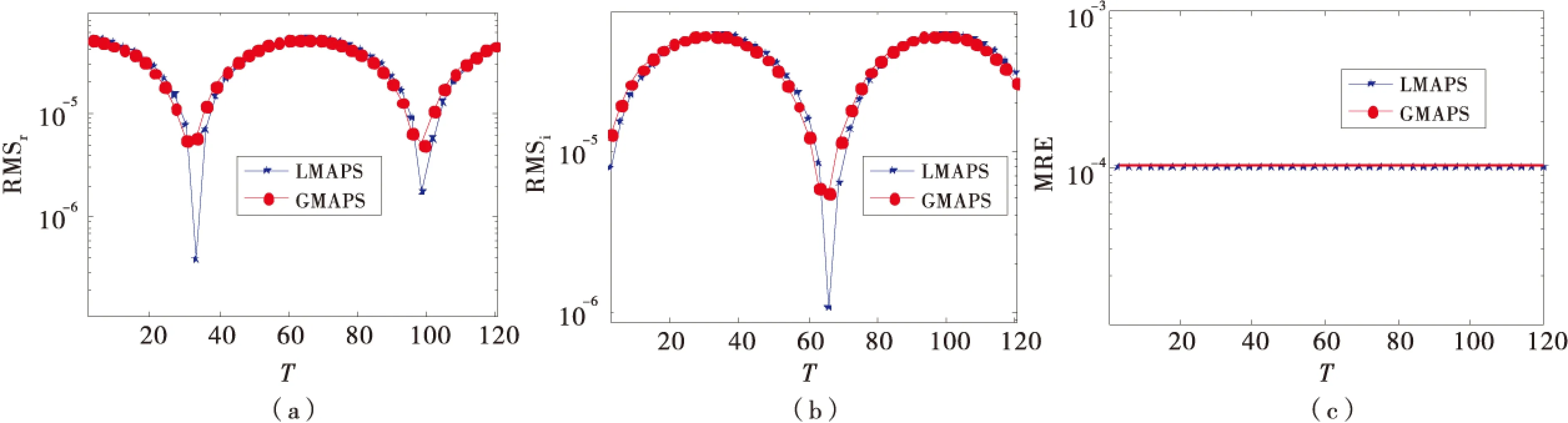
图2　LMAPS和GMAPS误差比较

图3　误差与形状参数c的关系，dt=0.01，T=40，ns=13

图4给出了局部近似特解法的误差随着ns的变化曲线．从图中可以看出，适当增加影响区域的插值点数可以提高精度．这是因为增加影响区域的插值点数可以提高控制方程的条件数[22]．虽然此时同时增加计算量，但是由于区域插值点数总小于总点数，该方法的计算量总比全局近似特解法的小．当ns增大到总点数时，两者的计算量相同．

图4　误差随ns的变化曲线dt=0.01，c=13

其次，分别减小空间步长dx，dy和时间步长dt，分析局部近似特解法和全局近似特解法的稳定性．图5表明局部近似特解法的收敛速度快，且可以通过采用较少的配点，保证同等的精度要求，因此可以进一步提高计算效率．图6表明随着时间步长dt的减小，局部近似特解法可收敛到一个更高的精度．图5和图6同时说明，局部近似特解法具有更高的稳定性．

图5　误差随dx，dy的变化曲线dt=0.01，c和ns取dx，dy对应的最优值

图6　误差随dt变化趋势ns=13，c=13

下面简要分析局部近似特解法和全局近似特解法的计算耗时．将计算分为两个阶段，零时刻的赋值阶段和时间方向的离散阶段．首先第一阶段，后者的矩阵需要赋值数为ni·ni+nb，前者的为ns·ni+nb，由于ns≪ni，因此前者的计算耗时比后者的少；其次是第二阶段，由于前者采用稀疏矩阵，在时间方向上每一步的计算耗时均比后者少．因此，局部近似特解法的计算耗时比全局近似特解法的少，图7验证了上述结论．

图7　计算耗时ns=13

3.2算例2：不规则区域

为进一步验证该方法的有效性，考虑如图8的不规则区域，其中边界点nb=136，内部点ni=625，总点数n=761．图9给出了对应不同时刻的相对误差曲面图(c=22，ns=13，dt=0.001)，图10～12显示了三个随机配点处模拟值与真实值的吻合程度，图13显示了布点数增加到10万时的计算耗时，数值结果表明局部近似特解法具有较高的精度和时间稳定性，且计算耗时少，可以有效地求解此类二维薛定谔方程．

图8　不规则区域及配点示意图

图9　不同时间T对应的相对误差曲面图

图10　随机配点(0.175，0.720)

图11　随机配点(0.130，0.275)

图12　随机配点(0.945，0.570)

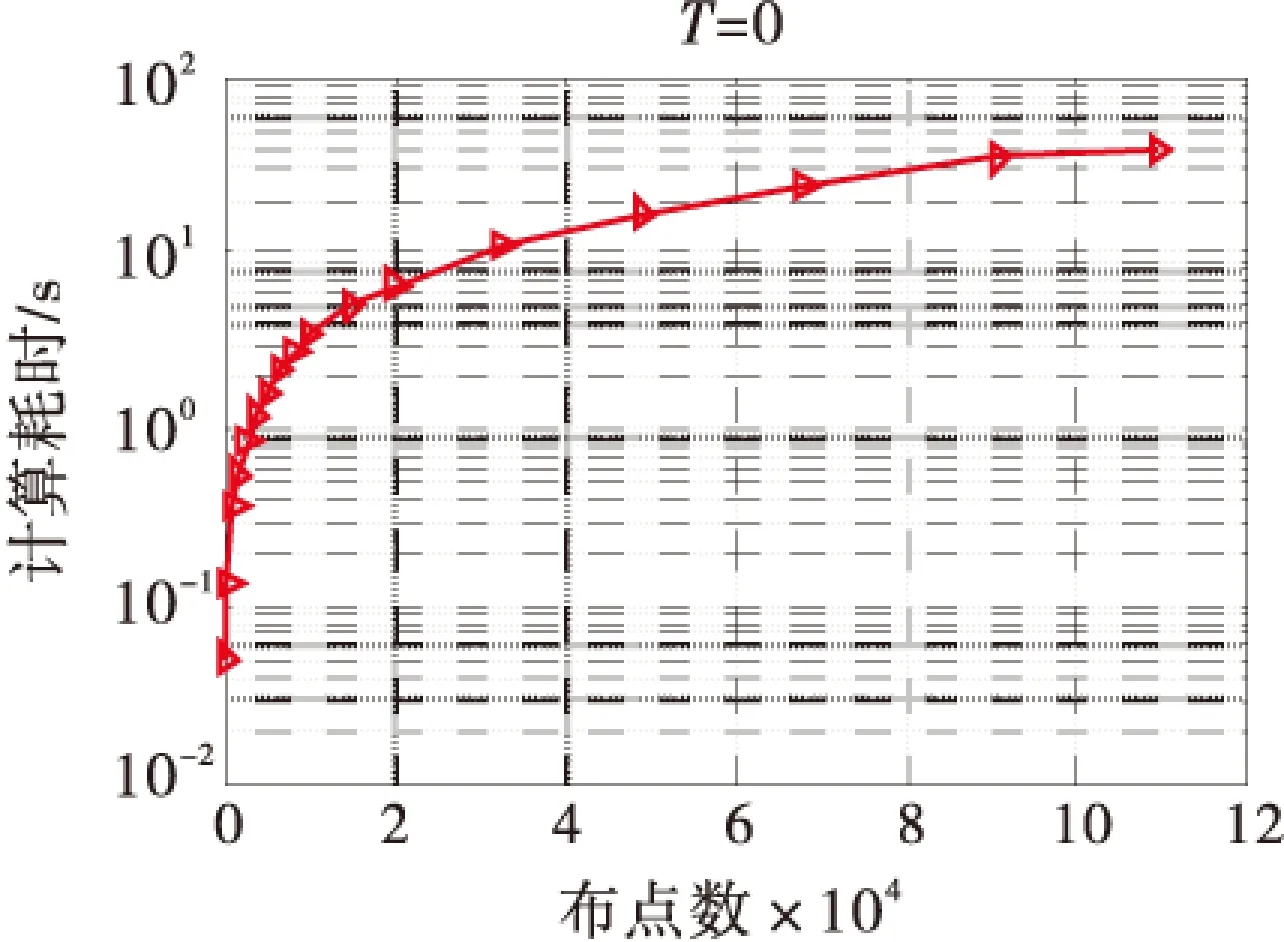
图13　计算耗时ns=13

4结语

本文采用基于MQ函数的局部近似特解法，模拟二维薛定谔方程．上文的算例表明，该方法能很好地解决这类问题，并且克服了全局方法对形状参数的敏感性和稠密矩阵带来的求解困难等问题．同时利用稀疏矩阵，大幅度提高了求解时域问题的计算效率．总之，该方法很好地继承了全局近似特解法的优点，同时改善了它的部分缺点，并在一定程度上提高了它的稳定性．鉴于该方法无网格的优点，可以将它推广到三维和大规模工程问题上[23]．对于三维问题，其矩阵将更加稠密．因此，需要对本文所提方法进行改进，如引进更有效的形状参数c，引入多尺度径向基函数等．

参考文献：

[1]宋祥，李画眉．变系数耦合非线性薛定谔方程的矢量孤子解：暗-亮孤子解[J]．浙江师范大学学报：自然科学版，2013(3)：294-298．

[2]宋诗艳，王晶，孟俊敏，等．深海内波非线性薛定谔方程的研究[J]．物理学报，2010(2)：1123-1129．

[3]李宏，孟祥东，张斯淇，等．用薛定谔方程和路径积分方法研究中子双缝衍射[J]．南开大学学报：自然科学版，2014(3)：68-73．

[4]刘登云，王剑波．用因式分解法求解薛定愕方程[J]．大学物理，1990(7)：13-15．

[5]宫建平．有限差分法求解薛定谔方程[J]．晋中学院学报，2014，31(3)：1-6．

[6]Tang D J． Generalized Matrix Numerov Solutions to the Schrödinger equation[D]． Singapore：National University of Singapore，2014．

[7]Filiz A，Ekici M，Sonmezoglu A． F-Expansion Method and New Exact Solutions of the Schrödinger-KdV Equation [J]．The Scientific World Journal，2014：1-14．

[8]王婵媛，石记松，陈文．基于径向基函数的Hermite配点法的薄膜自振分析[A]．中国土木工程学会教育工作委员会．第六届全国土木工程研究生学术论坛论文集[C]．中国土木工程学会教育工作委员会，2008：1．

[9]Kansa E J． Multiquadrics-A Scattered Data Approximation Scheme with Applications to Computational Fluid-dynamics-I Surface Approximations and Partial Derivative Estimates[J]．Computers & Mathematics with Applications，1990，19(8-9)：147-161．

[10] Duan Y，Hon Y C，Zhao W． Stability Estimate on Meshless Unsymmetric Collocation Method for Solving Boundary Value Problems [J]．Engineering Analysis with Boundary Elements，2013，37：666-672．

[11] Hardy R L． Multiquadric Equations of Topography and Other Irregular Surfaces[J]．Journal of Geophysical Research，1971，8 (76)：1905 -1915．

[12] Pang G F，Chen W，Fu Z J． Space-fractional Advection-dispersion Equations by the Kansa Method[J]．Journal of Computational Physics，2015，293：80-96．

[13] Yao G M． Local Radial Basis Function Methods for Solving Partial Differential Equations[D]． Hattiesburg： University of Southern Mississippi，2010．

[14] Islam S U，Vertnik R，Sarlera B． Local Radial Basis Function Collocation Method Along with Explicit Time Stepping for Hyperbolic Partial Differential Equations[J]．Applied Numerical Mathematics， 2013， 67：136-151．

[15] Khoshfetrat A，Abedini M J． Numerical Modeling of Long Waves in Shallow Water Using LRBF-DQ and Hybrid DQ/LRBF-DQ[J]．Ocean Modeling，2013，65：1-10．

[16] Yao G M，Kolibal J，Chen C S． A Localized Approach for the Method of Approximate Particular Solusions[J]．Computers and Mathematics with Applications，2011，61：2376-2387．

[17] Omohundro S M． Efficient Algorithms with Neural Network Behaviour [J]．Journal of Complex Systems， 1987，1：273-347．

[18] Su J B，Zhu F，Geng Y，et al． Numerical Study of Wave Overtopping Based on Local Method of Approximate Particular Solution Method [J]．Advanced in Mechanical Engineering，2014：1-9．

[19] Lin C Y，Gu M H，Young D L，et al． Localized Method of Approximate Particular Solutions with Cole-Hopf Transformation for Multi-dimensional Burgers Equations[J]．Engineering Analysis with Boundary Elements，2014，40：78-92．

[20] Zhang X Y，Tian H Y，Chen W． Local Method of Approximate Particular Solutions for Two-dimensional Unsteady Burgers' Equations[J]．Computers and Mathematics with Applications，2014，66：2425-2432．

[21] Fu Z J，Chen W，Ling L． Method of Approximate Particular Solutions for Constant-and Variable-order Fractional Diffusion Models[J]．Engineering Analysis with Boundary Elements，2015，57：37-46．

[22] Lin J，Chen W，Sze K Y． A New Radial Basis Function for Helmholtz Problems[J]．Engineering Analysis with Boundary Elements，2012，36(12)：1923-1930．

[23] 刘从建，陈文，王海涛，等．自适应快速多极正则化无网格法求解大规模三维位势问题[J]．应用数学和力学，2013，3(3)：259-271．

[责任编辑王康平]

收稿日期：2015-09-08

基金项目：国家杰出青年基金资助项目(11125208)；国家自然科学基金(11302069,11372097)；江苏省自然科学基金项目(BK20150795)；中央高校基本科研业务费专项资金资助(2015B11914)

通信作者：陈文(1967-)，男，教授，博士，主要研究方向为计算力学算法和软件．E-mail：chenwen@hhu.edu.cn

DOI：10.13393/j.cnki.issn.1672-948X.2016.01.011

中图分类号：O413.1

文献标识码：A

文章编号：1672-948X(2016)01-0051-06

Numerical Simulation of 2D Schrödinger Equation by Localized Method of Approximate Particular Solution Based on Radial Basis Functions

Hong YongxingChen WenLin Ji

(College of Mechanics & Materials, Hohai Univ., Nanjing 211100, China)

AbstractThe localized method of approximate particular solution (LMAPS) is a truly meshless collocation method with merits of high accuracy, rapid convergence and easy-to-program. In the LMAPS, the interest domain is divided into several subdomains; and in each subdomain, the localized low-rank matrix is formed based on the local nodes. And then a sparse system is constructed by reformulating the localized formulation into globalized form, which can be solved efficiently. In this paper, the LMAPS is applied to simulate 2D Schrödinger equation where the implicit-Euler scheme is used for time discretization; and the LMAPS is utilized for space discretization. Numerical experiments reveal the high accuracy, fast convergence and lower computational time of the LMAPS. And it has potential to engineering applications.

KeywordsImplicit-Euler;2D Schrödinger equation; Multiquadric function; localized method of approximate particular solution;global method of approximate particular solution