考虑均布侧压载荷的复合材料格栅加筋圆柱壳

袁军李叙华（ 海军装备部，陕西 西安，7005； 航天科技集团第四研究院，陕西 西安，7005）

考虑均布侧压载荷的复合材料格栅加筋圆柱壳

袁军1李叙华2
（1 海军装备部，陕西 西安，710025； 2 航天科技集团第四研究院，陕西 西安，710025）

本文基于特征值屈曲分析与多岛遗传优化方法，对均布侧压载荷作用下的复合材料格栅加筋圆柱壳的轴压承载性能进行优化设计。先对不考虑均布侧压载荷的复合材料格栅加筋圆柱壳轴压承载性能进行优化设计，得到结构最大轴压承载性能与质量设计空间之间的关系，然后再设计一系列不同大小的均布侧压载荷，包括内压及外压载荷，预先施加于复合材料格栅加筋圆柱壳，继而对其轴压承载性能进行优化设计，对比分析最大轴压承载性能与侧压载荷的关系，最后得出复杂载荷下复合材料格栅加筋圆柱壳的优化设计思路，为航空航天等领域中的相关优化设计提供参考。

侧压载荷；复合材料格栅；轴压承载性能；特征值屈曲分析

纤维增强树脂基复合材料具有比强度高、比刚度大、阻尼特性好、疲劳寿命长、结构可设计性等优点，故可广泛应用于航空航天等的工程结构中。采用加筋结构形式是提高复合材料构件承载能力的有效形式之一，而格栅加筋结构作为一种特殊的加筋结构，以较强的可设计性和多种优良性能备受关注。

先进复合材料格栅加筋结构（AGS）作为一种新型加筋结构形式，主要应用于航空航天器等的圆柱壳结构中，常见格栅加筋圆柱壳结构形式包括正交格栅构型圆柱壳、等格栅构型圆柱壳等，见图 1所示。吴德财、廖英强等［1-2］针对复合材料典型网格加筋结构稳定性进行研究，分析了不同网格形状对复合材料格栅加筋结构承载性能影响。龙连春等［3-4］对轴压或外压载荷下网格加筋承载性能进行了分析及优化，给出承载性能更优的结构设计方案。由于格栅加筋结构所承受的外载复杂多样，单一轴、内外压承载性能与复杂载荷下承载性能并不吻合，为满足其承载的要求，需要对复杂载荷下AGS圆柱壳结构进行优化，以充分发挥该结构卓越的承载能力。

目前，对于AGS圆柱壳结构的优化设计主要面临以下问题：1）求解AGS圆柱壳结构极限承载能力时，可选用不同的有限元数值计算方法，但不同的计算方法会使得计算结果的准确性、计算效率等各不相同，从中筛选出效率、准确性高的求解方法十分关键；2）不同载荷形式下，AGS圆柱壳优化设计参数与承载性能不同，如何高效优化复杂载荷下AGS圆柱壳承载性能是另一个关键问题。

本文基于特征值屈曲分析及多岛遗传优化算法，针对均布侧压载荷下正交格栅构型的AGS圆柱壳轴压承载能力进行了优化设计，通过对比不同均布侧压载荷下AGS圆柱壳优化设计方案以及轴压承载性能，给出了复杂载荷下AGS圆柱壳优化设计思路，为航空航天等领域中承载复杂载荷的复合材料格栅加筋圆柱壳优化设计提供了参考。

图1 不同格栅加筋构型圆柱壳（隐藏蒙皮）

1 基于特征值屈曲分析的AGS圆柱体承载性能研究

屈曲分析是一种用于确定结构出现不稳定时的屈曲临界载荷和屈曲模态（结构发生屈曲响应时的特征形状）的技术，其中，最低屈曲临界载荷即为本研究所涉及的承载能力；屈曲问题分析方法可分为特征值屈曲分析和非线性后屈曲分析。

特征值屈曲分析又称线性屈曲分析，在线性屈曲情况下，令结构刚度矩阵为 ，某参考载荷对应的初应力刚度阵为［K］，结构屈曲形状的特征向量为［S］；令屈曲临界载荷为［u］，则为应力刚度矩阵偏离结构刚度矩阵的比例因子（特征值）。由此，特征值屈曲的控制方程可表示为：

非线性后屈曲分析的常用方法为牛顿-拉普森法，简称N-R法。基于增量加载的N-R法迭代能够较好地模拟结构的屈曲失稳演化历程。根据最小势能原理，可得AGS圆柱壳分析的有限元控制平衡增量形式的方程［5］：

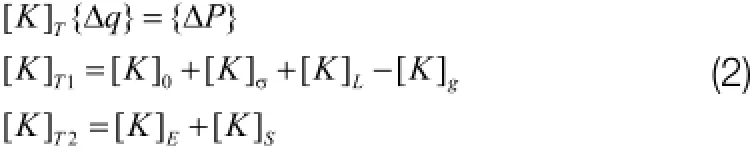
这种迭代方法虽然可以使每个载荷增量的末端解达到收敛，从而有效减少累积误差，但每次迭代都需重新计算结构的切线刚度和不平衡力，并不断校正平衡解，导致计算工作量较大。考虑到特征值屈曲分析的高效性，本文选用特征值屈曲分析方法对AGS圆柱壳轴压承载能力进行研究。

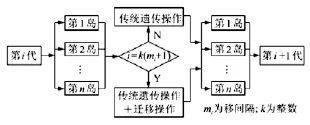
图 2 多岛遗传算法框图

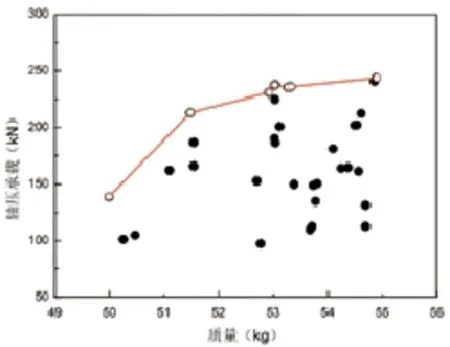
图3 无均布外压载荷作用的AGS圆柱壳轴压承载与质量设计空间

表1 材料性能

2 多岛遗传算法

AGS圆柱壳的轴压承载性能优化问题较为复杂，其目标函数具有多峰性、非线性等特点，采用多岛遗传算法能有效地搜索出该类问题的全局优化解。

遗传算法（TGA）于60年代由Holland 首次提出，主要借助生物进化过程中“适者生存”的规律，模仿生物进化过程中的遗传繁殖机制，对优化问题解空间的个体进行编码，然后对编码后的个体进行遗传操作，通过迭代从新种群中寻找含有最优解或较优解的组合［6］。

多岛遗传算法（MIGA）建立在传统遗传算法基础上。多岛遗传算法不同于传统遗传算法的特点是每个种群的个体被分成几个子群，这些子群称为“岛”。多岛遗传算法在优化过程中，首先利用初始值进行优化操作，初步达到收敛后，由于变异和迁移作用，在一个新的初值点开始重新进行遗传操作，如此重复操作，因此尽可能避免局部最优解，从而抑制了早熟现象的发生。图 2为多岛遗传算法的分析流程框图［7］。

3 均布侧压载荷下AGS圆柱壳轴压承载性能优化

为了进一步指导AGS的结构设计，本文对不同均布外压与均布内压载荷下AGS圆柱壳轴压承载能力进行优化。

以复合材料正交格栅加筋圆柱壳为例，其长度与内半径分别为3m、1.5m；蒙皮及筋条材料参数为：蒙皮层数为8，单层厚度为0.12mm，铺层设计为纵筋数量为30，环筋数量为9，筋条宽度为纵、环筋厚度分别为、。根据工艺需要各变量设计范围，如表 1所示。

3.1 均布外压载荷

1）当均布外压为零时，复合材料正交格栅加筋圆柱壳轴压承载与质量设计空间关系，如图 3所示。

对图 3所示设计空间的所有样本点进行筛选，将设计空间上边界样本点用空心圆进行表征并连接，从而得到复合材料正交格栅加筋圆柱壳最大轴压承载-质量曲线。

由该曲线分析可知：质量偏低时，其轴压承载性能随优化历程提升较快；而当质量偏高时，轴压承载性能提升较慢。其原因是：当质量偏低时，结构轴压承载表现为由光筒结构承载转变为格栅加筋结构承载，失稳模式发生本质变化，因此轴压承载提升效果明显；当质量偏高时，结构轴压承载表现为弱格栅承载与强格栅承载，失稳模式并无本质区别，因而承载能力提升效果较慢。

2）施加一系列不同数值大小的均布外压载荷时，复合材料正交格栅加筋圆柱壳最大轴压承载与质量曲线，如图 4所示。

由图 4可知：对于不同均布外压载荷，复合材料正交格栅加筋圆柱壳最大轴压承载与质量曲线有所区别。随外压载荷增大，最大轴压承载与质量曲线整体水平降低，结构最小质量明显提高。原因在于随外压载荷增大，格栅加筋圆柱壳内凹变形增大，相当于引入的缺陷程度加重，从而降低了结构轴压承载性能。

3.2 均布内压载荷

施加一系列不同均布内压载荷时，复合材料正交格栅加筋圆柱壳最大轴压承载与质量曲线，如图 5所示。

由图 5可知：对于不同均布内压载荷，复合材料正交格栅加筋圆柱壳最大轴压承载与质量曲线有所区别。在相同质量下，随内压载荷增大，最大轴压承载性能有所提高。原因在于随外压载荷增大，格栅加筋圆柱壳外凸变形逐渐增大，这在一定程度上提高了结构的抗弯刚度，从而提高其轴压承载性能。

另外，考虑到内压载荷较大时，格栅加筋圆柱壳将产生过大外凸变形，导致结构可能在较低的轴压载荷下发生失稳，因此可继续提高内压载荷，对复合材料格栅加筋圆柱轴压承载性能进行优化。在考虑质量约束前提下，结构最大轴压承载性能与内压载荷曲线图，如图 6所示。

由图 6可知：随均布内压载荷升高，复合材料正交格栅加筋圆柱壳轴压承载性能呈上升趋势。原因在于结构外凸在一定程度上提高了结构抗弯刚度等性能。当内压升高至某较高水平（0.78MPa）时，结构外凸变形较大，内压工况难以收敛，因而未得到其后续曲线。

图4 不同均布外压载荷作用下的AGS圆柱壳轴压承载与质量设计空间

图5 不同均布内压载荷作用下的AGS圆柱壳轴压承载与质量设计空间

图6 AGS圆柱壳轴压承载性能与均布内压载荷关系曲线图

4 结论

1）本文基于特征值屈曲分析及多岛遗传优化算法，针对均布侧压载荷作用下正交格栅构型的AGS

下转P25页

袁军，毕业于海军航空工程学院导弹武器系统工程专业，从事固体火箭发动机研制。