高阶容积卡尔曼滤波及其在目标跟踪中的应用
张龙, 崔乃刚, 杨峰,路菲,卢宝刚
(1.哈尔滨工业大学 航天工程系, 黑龙江 哈尔滨 150001; 2.北京航天长征飞行器研究所, 北京 100076)
高阶容积卡尔曼滤波及其在目标跟踪中的应用
张龙1, 崔乃刚1, 杨峰1,路菲1,卢宝刚2
(1.哈尔滨工业大学 航天工程系, 黑龙江 哈尔滨 150001; 2.北京航天长征飞行器研究所, 北京 100076)
摘要:针对传统的容积卡尔曼滤波(CKF)估计精度有限的问题,提出了一种基于任意阶容积规则的高阶容积卡尔曼滤波(HCKF)方法并应用于机动目标跟踪问题。传统的CKF采用三阶球面-相径容积规则,可获得优于其他非线性滤波如不敏卡尔曼滤波(UKF)的估计精度和数值稳定性 。为了进一步提高CKF的估计精度,在基于点的高斯近似滤波框架下,分别使用Genz积分方法和矩匹配法推导出任意阶的球面规则和相径规则,以此构造高阶球面-相径容积规则来计算高斯型积分,并建立高阶容积卡尔曼滤波算法。将提出的HCKF算法应用于机动目标跟踪问题中并进行数值仿真。仿真结果表明,相对于传统容积卡尔曼滤波,高阶容积卡尔曼滤波对目标位置和速度估计的精度分别提高了11%和24%,可获得更高的估计精度。
关键词:高阶容积卡尔曼滤波;目标跟踪;非线性系统;贝叶斯估计;球面相径规则;容积规则
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20160127.1137.034.html

本文针对CKF估计精度有限的问题提出了高阶容积卡尔曼滤波,推导了五阶球面-相径容积规则来近似高斯权值积分,在五阶容积规则的基础上建立高阶容积卡尔曼滤波算法模型和计算流程,并应用于三维空间中的机动目标跟踪系统。
1高阶球面-相径容积规则
1.1高斯权值积分近似方法
考虑如下非线性离散时间动力学系统:
(1)
(2)
式中:状态向量xk∈Rn,测量向量yk∈Rm;vk-1和wk是相互独立的零均值系统高斯白噪声和测量高斯白噪声,方差分别为Qk-1和Rk。
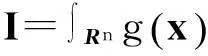
在容积规则中,考虑如下积分:
(3)
令x=rs,则式(3)可转换到球面-相径的坐标系统中,有
(4)
(5)
式中:ri和wr,i为计算相径积分的点和对应的权值,sj和ws,j为计算球面积分的点和对应的权值,Nr和Ns分别是相径积分和球面积分的点数。则高斯权值积分式可转换为
(6)
采用不同阶数的容积规则,并根据该规则选取不同容积点和权值,式(6)可得到不同的积分结果。目前,三阶球面-相径容积规则已经得到广泛的关注,下面给出五阶球面-相径容积规则。
1.2五阶球面-相径容积规则
文献[15-16]对球面规则进行了详细推导。由Genz积分方法[18-19],五阶球面规则满足:
(7)

(8)
(9)
(10)
(11)

(12)
选择r1为自由变量并令r1=0,解式(12),可得五阶相径规则的点和权值为
(13)
(14)
结合式(6)、(7)、(13)和(14),可以得到满足分布为x,~N(x;0,I)的五阶球面-相径容积规则
(15)

(16)
2高阶容积卡尔曼滤波
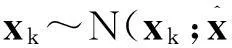
1)计算容积点
(17)

(18)

(19)
2)计算经状态方程传递后的容积点
建设单位作为投资主体,在组织招投标活动中,采取一系列手段来保护自身利益,有些明招暗定虚假招标,给参与投标活动的单位带来极大损失,主要表现在以下几个方面:
(20)
3)计算k+1时刻的状态预测值
(21)
其中权值wi分别为
(22)
4)估计k+1时刻的状态误差协方差阵
(23)
5)计算更新后的状态容积点
(24)

6)计算经过测量方程传递的容积点
(25)
7)计算k+1时刻的测量预测值
(26)
(27)
(28)
(29)
10)计算k+1时刻的状态估计值
(30)
11)估计k+1时刻的状态误差协方差阵
(31)
3数值仿真
为了表明高阶容积卡尔曼滤波算法的优越性能,将高阶容积滤波(五阶CKF)应用到三维空间中的目标跟踪系统中,并与不敏卡尔曼滤波(UKF)和传统容积滤波(三阶CKF)进行对比。
定义地面坐标系o-xyz的原点位于地面,ox指向东向,oy指向北向,oz与ox和oy成右手系,指向天向。假设目标在坐标系o-xyz中等高度机动飞行,目标跟踪系统动力学模型如下[9,16-17]:
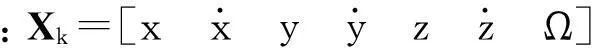
Q=diag(M1,M1,M1,M2)

假设测量雷达固定在地面坐标系原点,获取对目标的相对距离r、高低角η和方位角θ信息。假设目标的测量向量为y=[rθη]T,满足:
式中:w为测量噪声,其协方差阵R为
式中σr、σθ、σβ是雷达测量噪声的标准差。
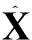
RMSEpos(k)=

图1为目标飞行的平面轨迹和雷达位置,“I”表示轨迹起点,“F”表示轨迹终点,“★”为雷达位置。图2~4分别给出了三种滤波方法对目标位置估计均方差、速度估计均方差和转速估计均方差的对比结果。由于0~40 s内三种滤波方法得到估计结果差别不大,故没有显示在图2~4中。由仿真结果可知,三阶CKF与UKF的估计精度较为接近并且三阶CKF精度稍高于UKF。五阶CKF的估计精度均高于UKF和三阶CKF,且数值稳定性更好。说明高阶球面-相径容积规则可以较大提高高斯权值积分的计算精度,进而提高滤波精度,体现了高阶球面-相径容积规则在估计精度方面的优越性。

表1 仿真参数设置

图1 目标飞行的平面轨迹和雷达位置Fig.1 The plane trajectory of the target and the radar's position

图2 目标位置的估计均方根误差Fig.2 The RMSE of the target position estimation
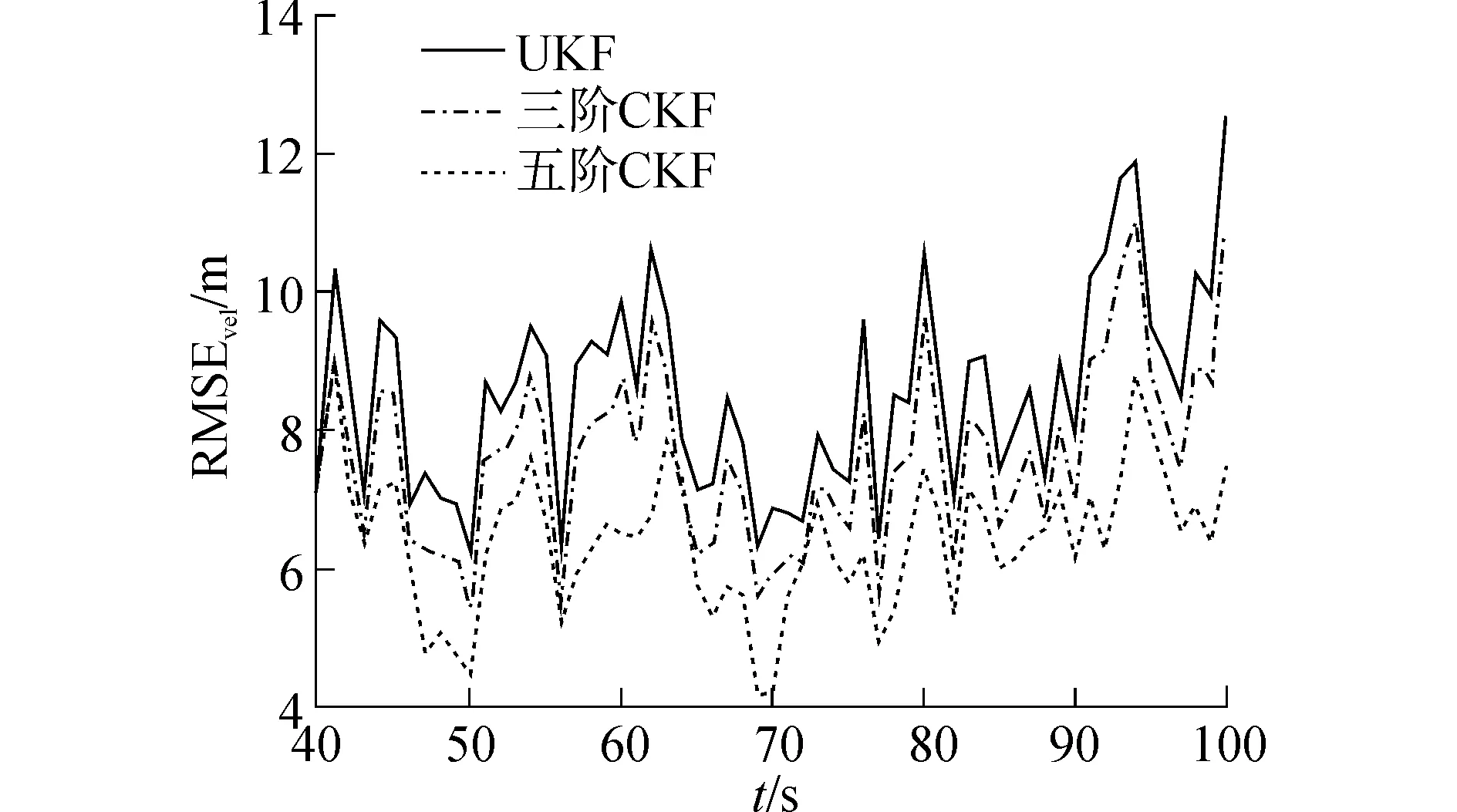
图3 目标速度的估计均方根误差Fig.3 The RMSE of the target velocity estimation
图5对比了10次随机打靶中各滤波方法计算所消耗的CPU时间。其中三阶CKF采用的容积点数最少,为14个容积点,因此算法计算量最小、运行时间最短。而基于高阶球面-相径容积规则的五阶CKF由于在时间更新和测量更新计算中采用99个容积点,提高了计算复杂度,因此算法运算时间最长。
表2给出了三种滤波方法对目标位置、速度、转速的均方根误差均值以及算法的容积点数和平均执行时间。

图4 目标转速的估计均方根误差Fig.4 The RMSE of the target turn rate estimation

图5 3种滤波方法的执行时间Fig.5 Execution time of the three methods
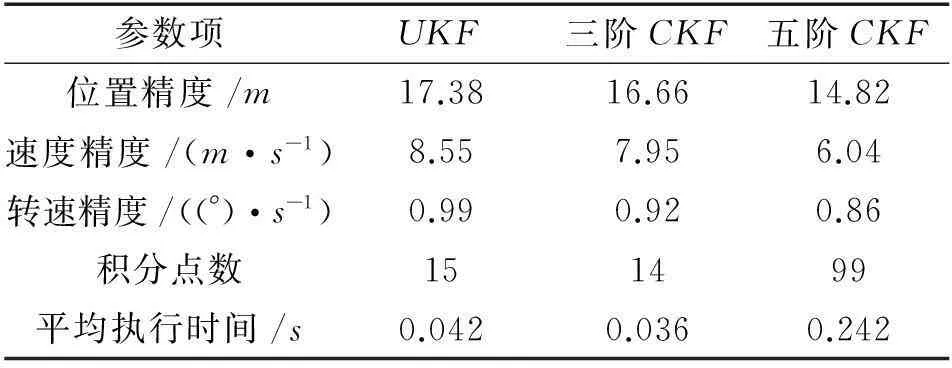
参数项UKF三阶CKF五阶CKF位置精度/m17.3816.6614.82速度精度/(m·s-1)8.557.956.04转速精度/((°)·s-1)0.990.920.86积分点数151499平均执行时间/s0.0420.0360.242
可以清楚看到,五阶CKF的估计精度明显优于其他两种滤波方法。但是相对于UKF和三阶CKF,五阶CKF采用的容积点数较多,运算时间较长。由此可知,五阶CKF在取得较高估计精度的同时,计算量的代价相对较大,特别是在系统状态向量维数n较高的情况下,其使用的容积点数几乎是三阶CKF的n倍。因此,五阶CKF适用于滤波时间间隔较长或对滤波实时性要求不高的高精度滤波系统中。此次仿真中五阶CKF算法的运算时间与滤波时间间隔相差较大,可以满足实时性需求。
4结论
本文针对传统容积卡尔曼滤波估计精度有限的问题,在基于点的高斯近似滤波框架下,提出高阶容积卡尔曼滤波算法HCKF。该算法采用Genz积分方法和矩匹配法分别推导出任意阶的球面规则和相径规则,以此构造高阶球面-相径容积规则。通过数学仿真可以得出以下结论:
1)对于三维空间中的机动目标跟踪问题,高阶CKF可获得优于UKF和传统CKF的估计精度和数值稳定性,表明高阶球面-相径容积规则可以较大提高高斯权值积分的计算精度,进而提高滤波精度,体现了高阶球面-相径容积规则在估计精度方面的优越性。
2)由于HCKF采用的容积点数量为2n2+1(n为状态向量维数),可知当状态向量维数较大时,采用的容积点较多,计算量相对CKF和UKF较大。因此,作者的下一个研究思路是通过降低状态向量维数或观测向量维数的方法在保持HCKF估计精度的同时明显减小算法计算量。
3)本文研究的HCKF是基于五阶球面-相径容积规则。实际上,采用不同阶数的球面规则和相径规则,就可以得到不同精度的容积规则。因此,一个可行的研究思路是设计更高阶的球面-相径容积滤波算法并对其分析。
参考文献:
[1]ITOK,XIONGKaiqi.Gaussianfiltersfornonlinearfilteringproblems[J].IEEEtransactionsonautomaticcontrol, 2000, 45(5): 910-927.
[2]FORBESJR.ExtendedKalmanfilterandsigmapointfilterapproachestoadaptivefiltering[C]//AIAAGuidance,Navigation,andControlConference.Toronto,Canada, 2010: 7748-7763.
[3]JULIERSJ,UHLMANNJK.Unscentedfilteringandnonlinearestimation[J].ProceedingsoftheIEEE, 2004, 92(3): 401-422.
[4]LIUXing,JIANGShoushan.ResearchontargettrackingbasedonunscentedKalmanfilter[J].Sensors&transducersjournal, 2013, 153(6): 13-21.
[5]王宏建, 徐金龙, 么洪飞, 等. 基于二阶差分滤波器的水下目标纯方位角跟踪[J]. 哈尔滨工程大学学报, 2014, 35(1): 87-92.
WANGHongjian,XUJinlong,YAOHongfei,etal.Researchonsecondorderdivideddifferencefilteralgorithmforunderwatertargetbearing-onlytracking[J].JournalofHarbinEngineeringUniversity, 2014, 35(1): 87-92.
[6]ARASARATNAMI,HAYKINS,ELLIOTTRJ,Discrete-timenonlinearfilteringalgorithmsusinggauss-hermitequadrature[J].ProceedingsoftheIEEE, 2007, 95(5): 953-977.
[7]JIABin,XINMing,CHENGYang.SparseGauss-Hermitequadraturefilterwithapplicationtospacecraftattitudeestimation[J].Journalofguidance,control,anddynamics, 2011, 34(2): 367-379.
[8]JIABin,XINMing,CHENGYang.Sparse-gridquadraturenonlinearfiltering[J].Automatica, 2012, 48(2): 327-341.
[9]ARASARATNAMI,HAYKINS.CubatureKalmanfilters[J].IEEEtransactionsonautomaticcontrol, 2009, 54(6): 1254-1269.
[10]ARASARATNAMI,HAYKINS,HURD,TR.CubatureKalmanfilteringforcontinuous-discretesystems:theoryandsimulations[J].IEEEtransactionsonsignalprocessing, 2010, 58(10): 4977-4993.
[11]FERNNDEZ-PRADESC,VIL-VALLSJ.Bayesiannonlinearfilteringusingquadratureandcubaturerulesappliedtosensordatafusionforpositioning[C]//IEEEInternationalConferenceonCommunications(ICC).CapeTown,SouthAfrica, 2010: 1-5.
[12]PESONENH,PICHÉR,Cubature-basedKalmanfiltersforpositioning[C]//7thWorkshoponPositioningNavigationandCommunication(WPNC).Dresden, 2010: 45-49.
[13]LIQiurong,SUNFeng.StrongtrackingcubatureKalmanfilteralgorithmforGPS/INSintegratednavigationsystem[C]//IEEEInternationalConferenceonMechatronicsandAutomation(ICMA).Takamatsu, 2013: 1113-1117.
[14]LIChao,GEQuanbo.SCKFforMAVattitudeestimation[C]//2011InternationalConferenceonMachineLearningandCybernetics.Guilin,China, 2011: 1313-1318.
[15]TAOSun,MINGXin.Hypersonicentryvehiclestateestimationusinghigh-degreecubatureKalmanfilter[C]//AIAAAtmosphericFlightMechanicsConference.Atlanta, 2014: 2383-2394.
[16]JIABin,XINMing,CHENGYang.Thehigh-degreecubatureKalmanfilter[C]//51stIEEEConferenceonDecisionandControl.Maui,USA, 2012: 4095-4100.
[17]JIABin,XINMing,CHENGYang.High-degreecubatureKalmanfilter[J].Automatica, 2013, 49(2): 510-518.
[18]GENZ,A.Fullysymmetricinterpolatoryrulesformultipleintegralsoverhyper-sphericalsurfaces[J].Journalofcomputationalandappliedmathematics, 2003, 157(1): 187-195.
[19]GENZA,MONAHANJ.AStochasticalgorithmforhigh-dimensionalintegralsoverunboundedregionswithGaussianweight[J].Journalofcomputationalandappliedmathematics, 1999, 112(1/2): 71-81.
收稿日期:2014-12-31.
基金项目:国家自然科学基金项目(61304236).
作者简介:张龙(1987-), 男,博士研究生; 通信作者:张龙, E-mail: zhanglong_hit@163.com.
doi:10.11990/jheu.201412079
中图分类号:V557
文献标志码:A
文章编号:1006-7043(2016)04-0573-06
High-degree cubature Kalman filter and its application in target tracking
ZHANG Long1,CUI Naigang1,YANG Feng1,LU Fei1,LU Baogang2
(1. Department of Astronautics Engineering, Harbin Institute of Technology, Harbin 150001, China; 2. Beijing Institute of Space Long March Vehicle, Beijing 100191, China)
Abstract:A high-order cubature Kalman filter (HCKF) based on the arbitrary-order cubature rule was proposed and applied to the maneuvering target tracking problem resulting from the limited precision of the conventional cubature Kalman filter (CKF). The conventional CKF, which employs the third-order spherical-radial cubature rule, can achieve better estimation precision and numerical stability than the other nonlinear filters, such as Unscented Kalman Filter(UKF). To further improve the estimation precision of CKF, in the framework of point-based Gaussian approximation filters, Genz's method and the moment-matching method were employed to deduce the arbitrary-order spherical rule and the radial rule, respectively. By combining the two rules, the high-order spherical-radial cubature rule was developed for computing Gaussian weighted integrals, and HCKF was proposed based on the high-order spherical-radial cubature rule. The proposed HCKF algorithm was applied to the maneuvering target tracking to test its performance. The simulation result shows that HCKF can achieve better estimation precision than conventional CKF, with the improvement of position and velocity estimates by 11% and 24% respectively.
Keywords:high-degree cubature Kalman filter; target tracking; nonlinear system; Bayesian filtering; spherical-radial rule; cubature rule
网络出版日期:2016-01-27.
崔乃刚(1965-), 男,教授,博士生导师.

