24种特征指标对轴承状态识别的性能研究*

程晓涵，　汪爱明，　花如祥，　孟国营

(中国矿业大学(北京)机电与信息工程学院　北京，100083)



24种特征指标对轴承状态识别的性能研究*

程晓涵，汪爱明，花如祥，孟国营

(中国矿业大学(北京)机电与信息工程学院北京，100083)

摘要要实现机械设备的故障诊断，关键是要找到对设备状态敏感性和聚类性强的特征指标。针对如何筛选出满足上述特点的指标，提出结合投影寻踪方法研究24种特征指标对轴承状态识别的敏感性和聚类性；以内圈故障为例，构造其故障振动的数学模型，计算得到24种特征指标并将其投影，提出最佳投射方向矩阵，研究在最佳投影方向矩阵下24种特征指标的投影分布特征；提出用极差系数、平均差系数、离散系数、主轴线相对系数和均值系数来研究24种特征指标对不同故障的敏感性和聚类性；借助美国西储大学轴承数据中心网站公开发布的轴承探伤测试数据集中的内圈故障进行验证。该方法能够为轴承的故障诊断筛选优质特征指标，保证故障识别的及时性和诊断准确性。

关键词24种特征指标； 投影寻踪； 最佳投影方向矩阵； 敏感性； 聚类性

引言

轴承故障从早期异常到功能故障是一个逐渐劣化的过程，利用时域特征指标进行故障识别存在严重的时间滞后性和应对被动性；频域信号对状态变化比较敏感，目前主要是借助典型频率分量来判断，但典型频率分量经常会有波动或偏差；信号的能量谱反映了信号中各频率成分的能量分布情况，也可以较好地描述信号频域特征的变化。因此，用于轴承故障识别的特征指标很多。

Vrabie等[1]将谱峭度用于轴承故障诊断，并定义其为一个过程距离高斯性的度量。Jack等[2]选用一定特征参量利用神经网络进行滚动轴承的故障识别。欧璐等[3]通过提取信号的时域和频域特征参数，并提取Hibert包络谱的频率特征参数和能量熵特征参数用于轴承的故障诊断。李少军[4]提出利用峭度指标、近似熵和功率谱熵三个特征指标，提出了融合多参数的滚动轴承故障特征提取方法。平鹏等[5]应用时域无量纲因子(峰值因子、脉冲因子、裕度因子、峭度因子、波形因子)和频域功率谱特征因子(均方频率、频率重心、频域方差、相关因子、谐波因子)诊断滚动轴承故障。国内外学者利用不同的特征参数采用不同的故障识别方法均取得了一定的成果，但针对目前丰富的特征指标对故障识别能力的影响方面的研究相对较少。周莹[6]结合BP神经网络和平均影响值(mean impact value,简称MIV)算法对常用的时域特征参数和频域特征参数做了特征筛选，根据仿真结果(即MIV值的大小)，得到8个敏感故障特征参量。

为实现轴承故障诊断功能，寻找一组能准确识别轴承运行状态并且对状态变化能快速反应的指标非常关键。笔者拟同时结合时域指标、频率指标和能量谱指标三方面的特征指标，借助投影寻踪方法研究特征指标对轴承不同故障类型和故障程度的聚类性和敏感性，从而为轴承的故障识别筛选出最佳的衡量指标。

124种特征指标的选取

用于轴承状态监测和故障诊断的特征指标很多，而且每个特征指标对轴承健康状态的规律性、敏感性和聚类性各不相同，为了选取优质特征指标以全面描述轴承运动状态，同时能够兼顾敏感性和稳定性，笔者搜集了常见的24种特征指标，涉及时域特征指标和频域特征指标，其中13个时域特征指标，有量纲特征指标6个，分别为：绝对均值、峰值、均方根值、方根幅值、方差、峰-峰值；无量纲特征指标最大的优点是受负载和转速等工况变化的影响小，特别适合实际应用的需要，可以从不同方面反映信号的变化，对故障表现出不同的敏感性。这里无量纲指标共有7个：偏斜度指标、峭度指标、峰值指标、波形指标、脉冲指标、裕度指标、变异系数；另外，一共采用11个频域特征指标：重心频率、均方频率、均方根频率、频率方差、频率标准差、谱峰稳定指数、5个频带相对功率谱能量(根据轴承频率范围，将频域平分成5个频带，每个频带带宽为Bf，分别计算每个频带的相对功率谱能量)。24个特征指标的定义表达式[7-8]如表1所示。

表1　时域与频域特征参数

Tab.1　Characteristic parameters of time domain and frequency domain

特征参数参数定义特征参数参数定义1.绝对均值xav=1N∑ni=1xi13.变异系数Kv=Dx/xav2.峰值xp=maxxi14.重心频率favg=∫∞0fpf()df∫∞0pf()df3.有效值xrms=1N∑ni=1x2i15.均方频率fb=∫∞0f2pf()df∫∞0pf()df4.方根幅值xr=1N∑Ni=1xi()216.均方根频率fbb=∑n2i=1f2i·Pfi()∑n2i=1Pfi()éëêêêêùûúúúú1/25.方差Dx=1N∑ni=1xi-xav()217.频率方差fv=∫∞0f-favg()2pf()df∫∞0pf()df6.峰-峰值xp-p=maxxi()-minxi()18.频率标准差frv=∫∞0f-favg()2pf()df∫∞0pf()dféëêêêùûúúú27.偏态指标α=16N∑Ni=1xi-xavDxæèçöø÷319.谱峰稳定指数S=∑n2i=1f2i·Pfi(){}∑n2i=1Pfi()∑n2i=1f4i·Pfi(){}∑n2i=1f2i·Pfi()8.峭度指标β=N24∑Ni=1xi-xavDxæèçöø÷4-3éëêêùûúú20.第1频带相对能量Er1=∫Bf0pf()df∫Fs0pf()df9.峰值指标Cf=xpxrms21.第2频带相对能量Er2=∫2BfBfpf()df∫Fs0pf()df10.波形指标Sf=xrmsxav22.第3频带相对能量Er3=∫3Bf2Bfpf()df∫Fs0pf()df11.脉冲指标If=xpxrms23.第4频带相对能量Er4=∫4Bf3Bfpf()df∫Fs0pf()df12.裕度指标CLf=xpxr24.第5频带相对能量Er5=∫5Bf4Bfpf()df∫Fs0pf()df

2基于投影寻踪的24种特征指标向量的建立

2.1振动数据预处理

对原始振动数据{ai,i=1,2,…,n}进行预处理，具体步骤为：

1) 对振动数据{ai,i=1,2,…,n}进行傅里叶变换得到{xi0,i=1,2,…,n}；

2) 按第1节中的各公式计算出能够描述轴承运行状态的24特征指标向量

2.2对24种特征指标向量进行投影处理

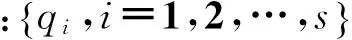
其中：p为训练样本的容量；n为特征指标的数量。

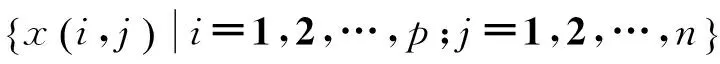
(1)

其中：a为单位长度向量。

3) 利用遗传算法建立最佳投影方向矩阵。传统的投影寻踪方法采用单一投影方向，投影值仅为一个投影值点，随着寻优过程的进行极有可能收敛到局部最优解，而且每次寻优得到的投影值偏差大，因此采用单一投影方向结果波动大、稳定性和可靠性差，给挖掘投影值潜藏的信息造成很大困难，甚至造成错误导向。因此，笔者提出采用最佳投影方向矩阵从多个有利方向进行投影观察，避免前述一系列问题，挖掘振动信号隐藏的设备信息。

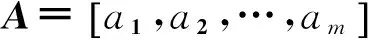
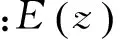
最大化目标函数

(4)

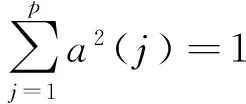
324种特征指标敏感度和聚类性衡量指标的确定

在筛选指标的过程中，好的特征指标应该同时具备两点基本要求：a.当描述轴承某一固定状态时，具有很好的稳定，即在最佳投影方向矩阵下的投影值应尽量聚集在某一主轴线附近并且要相对集中(理想状况下应该成一条直线)，离散度应尽可能小；b.当用其描述其他不同状态时，应具有良好的敏感性，即在最佳投影方向矩阵下的投影值主轴线和离散度应该变化较大。因此，笔者采用以下5种离散性指标来衡量各特征指标的优劣。

(5)

(6)

(7)

(8)

(9)

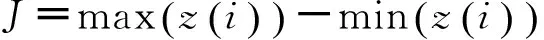
4仿真分析

轴承作为大型旋转机械设备的关键零部件，主要由滚子、内圈、外圈和保持架四部分组成，因此故障类型对应分为滚动体故障、内圈故障、外圈故障、保持架故障四大类。笔者以轴承内圈故障为例，研究24种特征指标对该故障状态的敏感度和聚类性，筛选出内圈故障的特征指标。

4.1内圈故障仿真信号的建立

当轴承某一元件出现损伤时，两个不平整的表面相互接触时会产生撞击，这种撞击会以一种冲击脉冲的形式传递出来，冲击脉冲信号的强弱可以直接体现撞击的强烈程度。笔者将建立型号为深沟球轴承6205的振动仿真数学模型，借助计算机仿真振动信号来进行分析，构建如下仿真信号来模拟轴承运动时的振动与撞击，以此来反映轴承的工作状态[1]

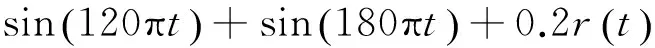
(10)

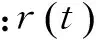
v(t)产生的振动可以分为两类：a.在旋转的过程中，元件表面损伤点与接触元件反复撞击产生的低频振动成分；b.整个轴承系统在故障撞击作用下产生的高频固有衰减振动成分。那么轴承内圈固有振动在故障撞击影响下而产生的信号，其形式如式(11)所示。内圈损伤为

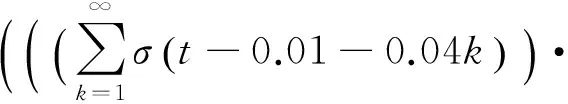
(11)

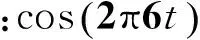
4.2投影分析

该例证中采用100个投影方向组成的最佳投影方向矩阵，按照上述第2节中的步骤计算轴承的24特征指标并投影，利用遗传算法搜索最佳投影方向矩阵100×24，输出内圈故障状态下24种特征指标在最佳投影方向矩阵下的投影值分布如图1所示。由图可以看出，在遗传算法寻优搜索的过程中投影值有可能出现浮动，如果采用单一投影方向极有可能发现不了投影值的分布特征，但是采用投影方向矩阵的话，在多个投影方向下统计分析投影值分布规律，能够得到可靠稳定的分析结果。

将图1中的投影值按照式(5)～(9)计算即可以得到内圈故障时的级差系数、平均差系数、离散系数、投影值主轴线相对系数和平均值系数，如表2所示。当内圈故障时，对表2计算结果进行总结：

1) 24个特征指标投影值的极差变化比较大的有：方差Dx>偏态指标α>峰值指标Cf>有效值xrms>裕度指标CLf>峰值xp；

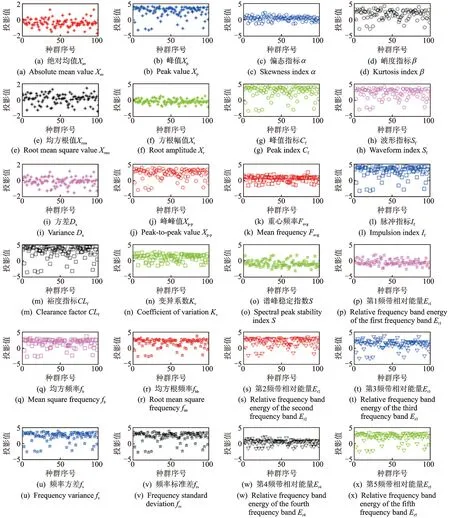
图1　内圈故障时24种特征指标在最佳投影方向矩阵下的投影值分布情况Fig.1　Projections distribution of 24 characteristic indexes under the best characteristic direction matrix when inner ring fault

2) 4个特征指标投影值的平均差变化比较大的有：有效值xrms>方差Dx>偏态指标α>峰值指标Cf>脉冲指标If>裕度指标CLf；

3) 24个特征指标投影值的离散度变化比较大的有：偏态指标α>峰值指标Cf>脉冲指标If>峰值xp>裕度指标CLf>有效值xrms；

4) 4个特征指标投影值的主轴线变化比较大的有：方差Dx>有效值xrms>偏态指标α>峰值指标Cf>裕度指标CLf>第一频带相对能量Er1；

5) 24个特征指标投影值的均值变化比较大的有：方差Dx>裕度指标CLf>脉冲指标If>偏态指标α>峰值指标Cf>有效值xrms。

表2　内圈故障相对于正常状态下的24种特征指标的4种系数

通过上述分析可知，相对于正常状态下，方差Dx、偏态指标α、峰值指标Cf、有效值xrms、裕度指标CLf、脉冲指标If和峰值xp这7个特征指标对内圈发生故障比较敏感，而且由相对离散系数可看出这些指标的聚类性也比较好，因此，这些指标可以用作监测和评估轴承运行状态是否良好的衡量指标。

5实验数据分析

文章借助美国西储大学轴承数据中心网站公开发布的轴承探伤测试数据集，针对深沟球轴承6205内圈故障尺寸为0.177 8 mm的监测数据进行分析和验证。按照2.1节和2.2节提出的方法进行投影，然后按照第3节中式(5)～(9)计算投影值分布的5个系数指标，当内圈产生故障时，总结计算结果：

1) 24个特征指标投影值的极差变化比较大的有：偏态指标α>裕度指标CLf>峰值指标Cf>脉冲指标If>峰值xp>有效值xrms；

2) 24个特征指标投影值的平均差变化比较大的有：偏态指标α>有效值xrms>方差Dx>裕度指标CLf>峰值指标Cf>脉冲指标If；

3) 24个特征指标投影值的离散度变化比较大的有：偏态指标α>裕度指标CLf>峰值指标Cf>脉冲指标If>峰值xp>有效值xrms；

4) 24个特征指标投影值的主轴线变化比较大的有：偏态指标α>方差Dx>有效值xrms>第1频带相对能量Er1>峰值指标Cf>裕度指标CLf；

5) 24个特征指标投影值的均值变化比较大的有：方差Dx>裕度指标CLf>有效值xrms>脉冲指标If>峰值指标Cf>偏态指标α。

因此，通过实验故障数据验证，方差Dx、偏态指标α、峰值指标Cf、有效值xrms、裕度指标CLf、脉冲指标If和峰值xp这7个特征指标对内圈发生故障比较敏感且聚类性较好，分析结果与模拟结果基本吻合，从而证明结合投影寻踪方法，利用最佳投影方向矩阵能够筛选出比较优质的特征指标用于轴承状态监测和故障识别。

6筛选出的特征指标提高轴承故障识别的能力

为了验证使用第4，5节筛选出的7个特征指标能够提高滚动轴承的故障识别能力，同样借用美国某网站公开发布的轴承探伤测试数据集，分别提取正常状态、内圈故障、滚动体故障和外圈故障下的监测数据并计算各状态下的24种特征指标，然后对各种状态下的24种特征指标进行投影，对其特点进行分析对比。图2(a)所示为采用24种特征指标进行投影的投影值分布特点，可以看出：正常状态下投影值(☆所示)聚集在纵坐标为1的轴线附近，滚动体故障状态下投影值(×所示)聚集在纵坐标为-1的轴线附近，但是内圈故障(△所示)和外圈故障(*所示)两种状态下的投影值发生了重叠，不利于故障识别，需要针对这两种状态进行单独的投影才能区分开来(如图2(b)所示)。由此可见，利用24种特征指标虽然具备一定的故障识别能力，但是一些敏感性和聚类性差的指标甚至起到干扰作用，容易出现投影值混叠现象，给故障识别造成困难。

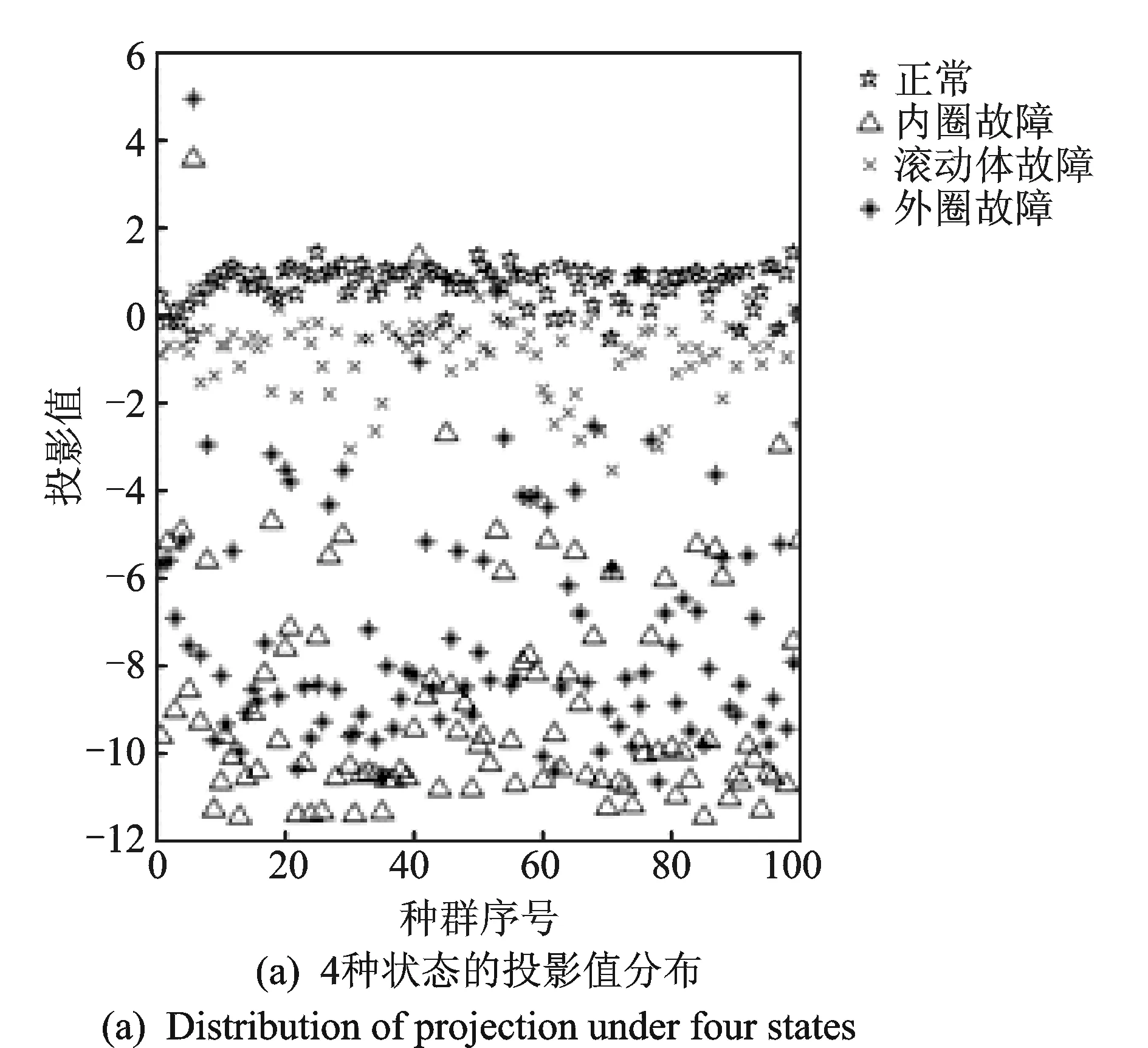
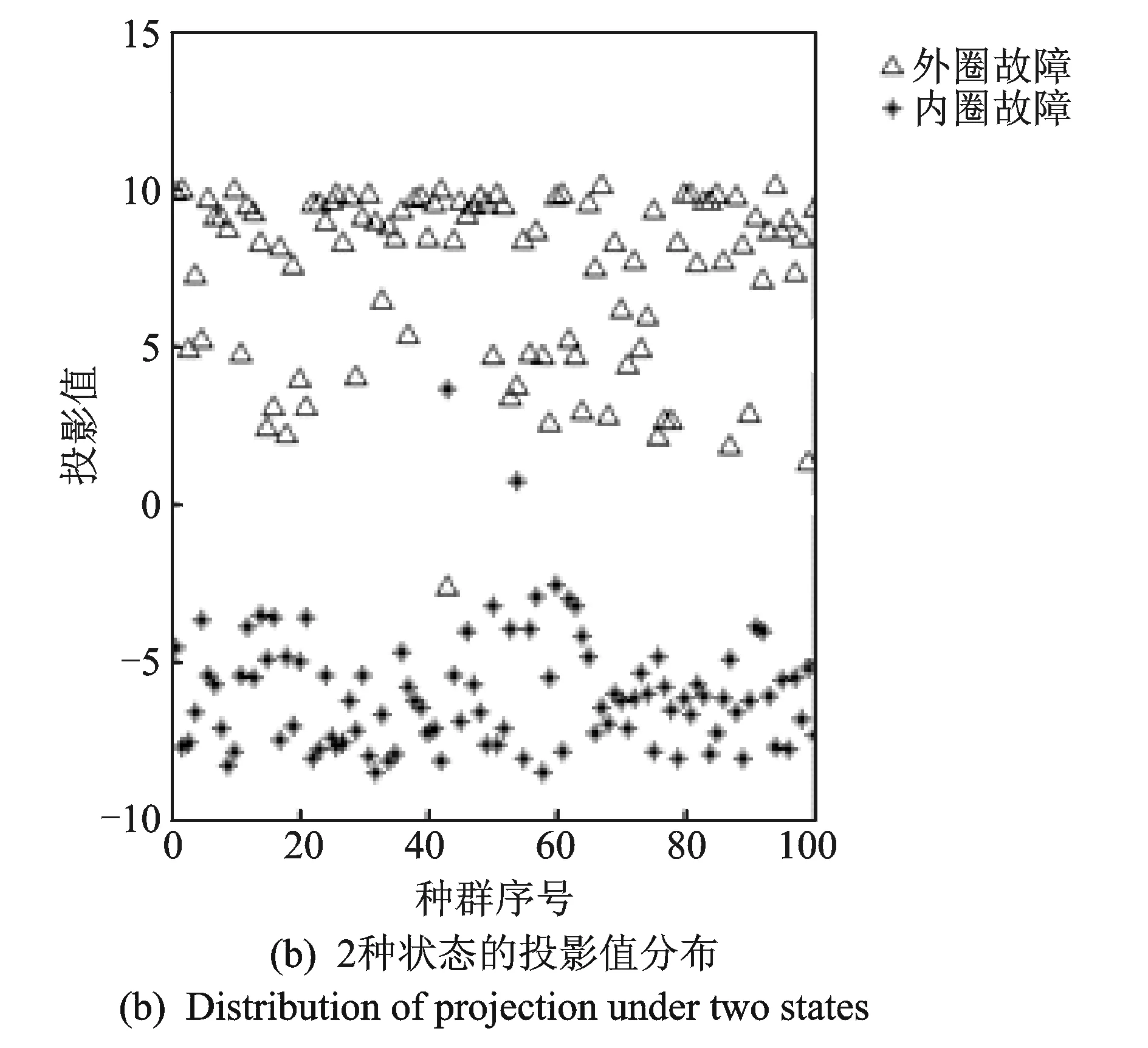
图2　采用24种特征指标进行故障识别时的投影值分布Fig.2　Distribution of projection when 24 characteristic indexes used for fault diagnosis

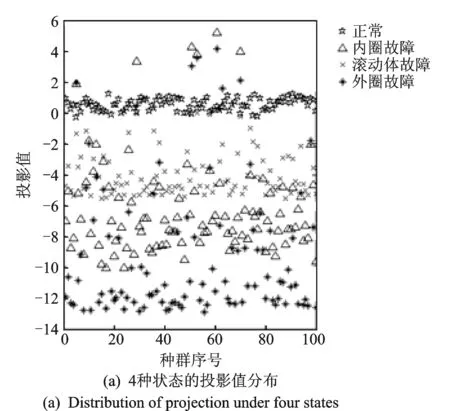
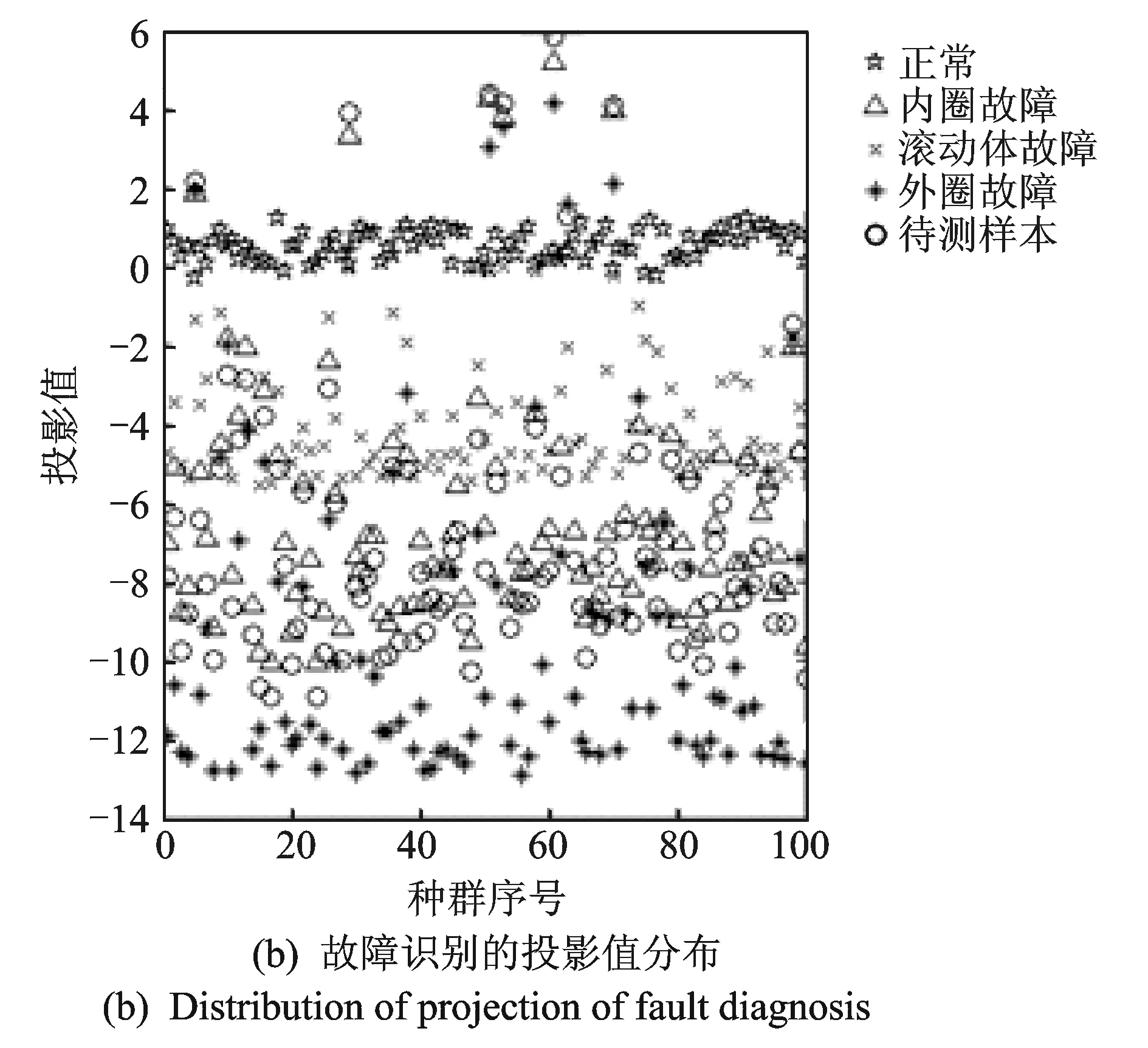
图3　采用7种特征指标进行故障识别时的投影值分布Fig.3　Distribution of projection when 7 characteristic indexes used for fault diagnosis

利用第4，5节筛选出的7个特征指标同样运用投影寻踪的方法进行投影，其投影值分布特点如图3(a)所示，正常状态下投影值(☆所示)聚集在纵坐标为0的轴线附近，滚动体故障状态下投影值(×所示)聚集在纵坐标为-4的轴线附近，内圈故障状态下投影值(△所示)聚集在纵坐标为-8的轴线附近，外圈故障状态下投影值(*所示)聚集在纵坐标为-12的轴线附近，没有发生明显的混叠现象，提高了轴承故障识别的能力。随机地提取某一时刻的一个待测样本数据，在同样的投影方向矩阵下进行投影，通过观察投影的分布区域实现故障识别。如图3(b)所示，待测样本投影值(○所示)基本与内圈故障重叠，因此可以判断待测样本处于内圈故障的状态。

7结束语

笔者以轴承内圈故障为例，通过建立相应的数学模型来模拟轴承故障信号，提出结合投影寻踪方法，研究24种常用特征指标对轴承故障状态的聚类性和敏感性，提出利用极差系数、平均差系数、离散度系数、主轴线相对系数和平均值系数来衡量各特征指标敏感性和聚类性。提出搜索最佳投射方向矩阵，有效地避免了单一投射方向下在寻优过程中对新空间的探索能力有限、容易收敛到局部最优解、结果稳定性可靠性差的缺点。最后结合西储大学的故障数据进行了验证，实验结果与理论分析结果基本一致，并且能够提高轴承的故障识别能力，从而证明了该方法的可行性和使用价值。

笔者提出的方法能够为轴承的安全运行监测和故障诊断筛选优质特征指标，保证轴承故障发现及时，故障诊断更加准确和可靠。

参考文献

[1]Vrabie V, Granjon P, Maroni C, et al. Application of spectral kurtosis to bearing fault detection in induction motors[J]. International Conference on Acoustical & Vibratory Surveillance Methods & Diagnostic Techniques, 2004,3(5):31-33.

[2]Jack L B, Nandi A K, Mccormick A C. Diagnosis of rolling element bearing faults using radial basis function networks [J]. Applied Signal Processing, 1999,6(1):25-32.

[3]欧璐,于德介,王翠亭. 拉普拉斯特征向量相关谱及其在滚动轴承故障诊断中的应用[J]. 振动工程学报,2014,27(5):748-754.

Ou Lu, Yu Dejie, Wang Cuiting. Correlation spectrum of laplacian eigenvectors and its applications to rolling bearing fault diagnosis.[J]. Journal of Vibration Engineering, 2014,27(5):748-754. (in Chinese)

[4]李少军. 滚动轴承故障诊断的多参数融合特征提取方法研究[D].北京：北京交通大学,2011.

[5]平鹏,张万斌,徐泽宁. 时域及功率谱特征因子诊断轴承故障的实验研究[J]. 振动、测试与诊断,1991,11(4):38-42.

Ping Peng, Zhang Wanbin, Xu Zening. Experimental research in diagnosis of bearing fault by time domain and power spectrum characteristic factors[J]. Journal of Vibration, Measurement & Diagnosis, 1991,11(4):38-42. (in Chinese)

[6]周莹. 基于MIV特征筛选和BP神经网络的滚动轴承故障诊断技术研究[D].北京：北京交通大学,2011.

[7]刘永斌. 基于非线性信号分析的滚动轴承状态监测诊断研究[D]. 合肥：中国科学技术大学,2011.

[8]李力,廖湘辉,张圆. 循环平稳度无量纲指标应用于滚动轴承状态分类[J]. 机械传动，2005,29(3): 21-23.

Li Li, Liao Xianghui, Zhang Yuan. Degree of cyclostation dimensionless index is applied to rolling bearing status classification[J]. Mechanical Drive，2005,29(3):21-23. (in Chinese)

[9]Maechler M, Mertin D, Schimert J. Projection pursuit learning networks for regression[C]∥Proceedings 2: International IEEE Conference Tools Artificial Intelligence. N.J： IEEE，1990:350-358.

[10]Miyoshi T. Near-fuzzy projection pursuit regression [C]∥IEEE International Conference Neural Networks. N.J.: IEEE, 1995:266-270.

[11]Hwang J N. The cascade-correlation learing: a projection pursuit learning perspective[C]∥IEEE Transaction Neural Networks. N.J.: IEEE, 1996:278-289.

[12]Fu Qiang, Lu Tieguang, Fu Hong. Applying PPE model based on raga to classify and evaluate soil grade[J]. Chinese Geographical Science, 2002, 12(2):136-141.

[13]Safavian S R，Rabiee H R，Fardanesh M. Projection pursuit image compression with variable block size segmentation[C]∥IEEE Signal Process Letters. N.J.: IEEE, 1997,4(5):117-120.

E-mail:chengxh212@163.com

doi:10.16450/j.cnki.issn.1004-6801.2016.02.024

收稿日期：2015-01-15；修回日期：2015-04-27

中图分类号TP277； TN911.7； TH165+.3

第一作者简介：程晓涵，女，1986年3月生，博士、讲师。主要研究方向为故障诊断与预知维护。曾发表《基于投影寻踪的旋转设备潜在故障识别方法》(《振动、测试与诊断》2015年第35卷第3期)等论文。

*国家自然科学基金资助项目(U1361127)；北京市教育委员会科学研究与研究生培养共建项目；中央高校基本科研业务费项目(2013QJ02)