压电式力传感器的低频补偿方法及实验验证①

陈江攀，　程　伟，　李　名

(北京航空航天大学航空科学与工程学院　北京，100191)



压电式力传感器的低频补偿方法及实验验证①

陈江攀，程伟，李名

(北京航空航天大学航空科学与工程学院北京，100191)

摘要提出了一种压电式力传感器低频响应特性的补偿方法,该方法是在频域上完成的。首先，对压电式力传感器的输出信号进行后处理，将输出信号与补偿函数相乘即可获得补偿后的输出信号，其中，补偿函数是压电式力传感器放电时间常数的函数；然后，以P5H压电陶瓷片为例，分别对其施加已知的阶跃外力和低频简谐外力，并分别将补偿前后的测试结果与已知外力进行对比，从而实现对该方法的实验验证。验证结果表明：该方法可以对压电式力传感器的低频响应特性进行有效的补偿。

关键词压电式力传感器； 低频补偿； 补偿函数； 频响函数； P5H压电陶瓷片

引言

航天器的活动部件在轨工作时所产生的微振动会对其成像质量和指向精度等关键性能产生较大的影响[1-4]，因此必须在地面开展对航天器活动部件微振动特性的测试。目前，国内外对航天器活动部件微振动特性的测试使用的都是微振动六分量测试平台。压电式力传感器由于具有高灵敏度、高分辨率、宽频响、宽测量范围等特点[5]，已成为微振动六分量测试平台最理想的传感器。然而，压电式力传感器存在一个较为明显的缺陷，即低频响应特性较差[6]，低频区的数据可信程度较低。因此，开展对该传感器低频响应特性补偿方法的研究十分必要。

压电式力传感器低频响应特性的补偿方法有：a.改变压电式力传感器的结构和设计参数；b.对压电式力传感器的输出信号进行后处理。通常情况下，第1种方法往往受到客观条件的限制，较难实现[7]。本研究采用第2种方法，提出了一种压电式力传感器低频响应特性的补偿方法，并以P5H压电陶瓷片为例对该方法进行了验证。结果表明，该方法可以对压电式力传感器的低频响应特性进行有效的补偿，为测试该平台的设计和改进提供了新思路。

1补偿方法的基本原理

压电式力传感器的等效电路及其实际运用电路参见文献[8-10]。压电式力传感器所受外力F(t)与放大器的输出电压U(t)的微分方程[5]为

(1)

其中：e为压电常数；A为压电元件的工作面积；R和C分别为等效电阻和等效电容。

将式(1)两端同时进行傅里叶变换[11]可得

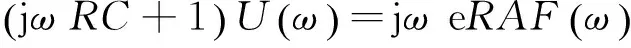
(2)

其中：j为虚数单位；ω为角频率。

由式(2)可得，压电式力传感器的输出电压U(ω)与所受外力F(ω)之间的关系为

(3)

其中：K=eA/C，为压电式力传感器的电压灵敏度；τ=RC，为压电式力传感器的放电时间常数。

通常情况下，将压电式力传感器的输出电压U(t)除以电压灵敏度K即可获得传感器对所受外力F(t)的测试结果Fc(t)，即

(4)

由于K为常数，将式(4)两端同时进行傅里叶变换,可得

(5)

将式(3)代入式(5)可得

(6)

由式(6)可得，压电式力传感器测试结果Fc(ω)与所受外力F(ω)之间的频响函数H(ω)为

(7)

由式(7)可得，该频响函数的幅值β(ω)和相位θ(ω)分别为

(8)

由式(8)得，当ω处于低频区时，压电式力传感器的响应特性较差，测试结果Fc(ω)与所受外力F(ω)在幅值和相位上均存在一定的偏差；而当ω处于高频区时，压电式力传感器的响应特性则较为理想。

理想的压电式力传感器在其测试范围内的频响函数应为

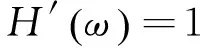
(9)

则将式(9)所示的频响函数H′(ω)除以式(7)所示的频响函数H(ω),可获得压电式力传感器的补偿函数B(ω)，即

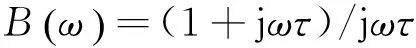
(10)

其中：补偿函数B(ω)为放电时间常数τ的函数。

将式(6)两端同时乘以补偿函数B(ω)，可得补偿后的测试结果Fb(ω)，即

(11)

由式(11)可得，将压电式力传感器的频域测试结果Fc(ω)乘以补偿函数B(ω)，即可获得补偿后压电式力传感器的频域测试结果Fb(ω)，该测试结果与压电式力传感器所受的外力一致。

2实验验证

本研究以P5H压电陶瓷片为例对该方法进行了实验验证。实验分为两部分：a.对P5H压电陶瓷片的电压灵敏度K和放电时间常数τ进行辨识，从而确定出补偿函数B(ω)；b.对P5H压电陶瓷片在已知的阶跃外力和简谐外力作用下的测试结果进行补偿，并将补偿结果与已知外力进行对比，从而验证本研究所提出的方法。

2.1参数辨识

由文献[6,12]可知，压电式力传感器在阶跃外力作用下的电压响应为

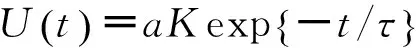
(12)

其中：a为阶跃外力的幅值；K为电压灵敏度；τ为放电时间常数。

由式(12)可得，若获得压电式力传感器在阶跃外力作用下的响应曲线，即可辨识出电压灵敏度K和放电时间常数τ。本研究就是通过测试压电陶瓷片在阶跃外力作用下的响应，然后对测试结果进行曲线拟合，从而进行参数辨识。

在实验中，通过特制的夹具将压电陶瓷片压紧并固定在大质量刚性实验台上。夹具由固定部分和受力部分组成，且在受力部分上固定有电磁铁。当电磁铁通电时，将标准砝码吸附在电磁铁上，待压电陶瓷片放电到零后，突然对电磁铁断电，在重力的作用下砝码将会脱离电磁铁，从而实现对压电陶瓷片施加正阶跃外力。为了提高辨识精度，本研究使用LMS数据采集系统分别对压电陶瓷片在9.8 N(1 kg砝码)、19.6 N(2 kg砝码)和29.4 N(3 kg砝码)阶跃外力作用下的电压时域响应进行了测试。实验装置实物照片见图1，测试结果见图2。

图1　实验装置实物照片Fig.1　Picture of experimental device

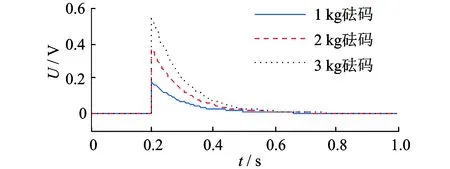
图2　压电陶瓷片响应曲线Fig.2　Response curve of piezoelectric ceramic piece

利用MATLAB曲线拟合工具对图2所示3条曲线的衰减部分进行拟合，拟合结果为

(13)

3条曲线的拟合优度见表1。

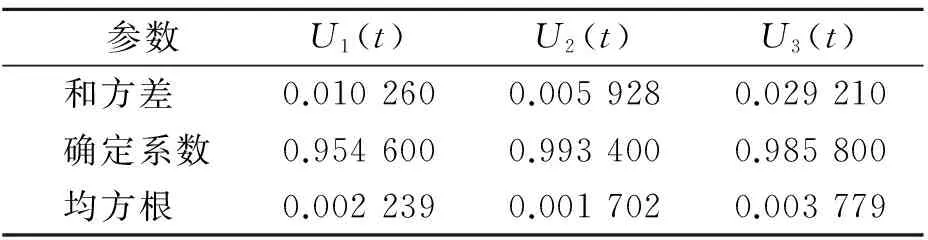
表1　曲线拟合优度

由表1可得，式(13)可以对图2所示的测试结果进行有效的拟合。由式(13)可得，压电陶瓷片的电压灵敏度K和放电时间常数τ分别为

(14)

因此可得P5H压电陶瓷片的补偿函数为

(15)

2.2方法验证

为了验证本研究所提出的方法，分别对P5H压电陶瓷片在已知阶跃外力和简谐外力作用下的测试结果进行了补偿。对于阶跃外力而言，其加载方式与图1所示一致，砝码的质量为1.5 kg，即阶跃外力的幅值为14.7 N。图3给出了P5H压电陶瓷片在阶跃外力作用F下补偿前后的测试结果。

图3　阶跃外力作用下补偿前后测试结果对比图Fig.3　Contrast figure of testing result before and after compensation under the action of step force

对于简谐外力而言，其加载方式为：在夹具的受力部分上悬挂一根软弹簧，在软弹簧的另一端悬挂一个质量块，当质量块在某初始条件的作用下上下运动时，将会对压电陶瓷片施加一个简谐外力，且该简谐外力的表达式为

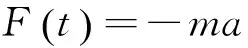
(16)

其中：m为质量块的质量；a为质量块的加速度。

由式(16)可得，该简谐外力的大小与质量块的加速度成正比，因此在质量块上粘贴有一个加速度传感器，用于测试质量块在振动过程中的加速度。本研究所使用的加速度传感器是电容式加速度传感器，其测试范围可达到0 Hz。实验装置照片见图4。

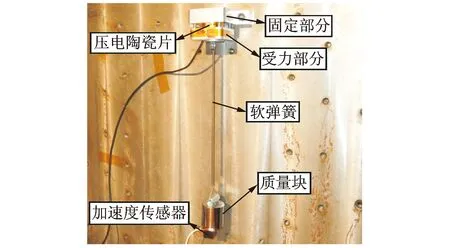
图4　简谐外力加载装置照片Fig.4　Picture of harmonic force loading device

在实验过程中，使用LMS数据采集系统分别对软弹簧-质量系统作简谐振动时质量块的加速度以及压电陶瓷片输出电压的时域响应进行了测试，测试结果参见图5和图6。

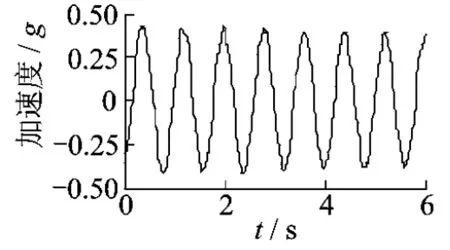
图5　加速度传感器时域测试结果Fig.5　Testing result of acceleration sensor in time domain

图6　输出电压时域测试结果　Fig.6　Testing result of out-put voltage in time domain

将图5所示的加速度经式(16)计算并进行傅里叶变换可得简谐外力的频域结果F(ω)；将图6所示的压电陶瓷片的输出电压经式(4)计算并进行傅里叶变换可得压电陶瓷片对简谐外力补偿前的频域测试结果Fc(ω)；图7和图8分别给出了简谐外力和补偿前测试结果的频域幅值曲线。

将补偿前的频域测试结果Fc(ω)与式(15)所示的补偿函数B(ω)相乘即可获得补偿后的频域测试结果Fb(ω)。图9为补偿后测试结果。

图7　简谐外力频域结果　　　　　　　　图8　补偿前频域测试结果　　　　　　图9　补偿后频域测试结果 Fig.7　Harmonic force in frequency domain 　Fig.8　Testing result before compensation in frequency domain　Fig.9　Testing result after compensation in frequency domain

2.3结论

由图2知，压电式力传感器的高频响应特性良好，但是其低频响应特性较差;由图3知，笔者的方法可以对压电式力传感器在阶跃外力作用下的低频响应特性进行有效补偿；由图7知，简谐外力的振动频率为1.25 Hz，振动幅值为3.812 N，处于低频区；由图8知，补偿前的测试结果为2.338 N，与简谐外力的振动幅值相差较大；由图9知，补偿后的测试结果为3.807 N，与简谐外力的振动幅值基本一致。

此外，经计算可得，简谐外力和补偿前后测试结果在1.25 Hz处的振动相位分别为0.57 π,0.83 π和0.54 π，即补偿前的振动相位与简谐外力的振动相位相差较大，而补偿后的振动相位与简谐外力的振动相位基本一致。

3结束语

本研究提出了一种压电式力传感器低频响应特性的补偿方法，并以P5H压电陶瓷片为例，通过实验测试对该方法进行了验证。结果表明：笔者提出的方法可以对压电式力传感器的低频响应特性进行有效的补偿。本研究所得的结论为用于航天器活动部件微振动特性测试的压电式微振动六分量测试平台的设计和改进提供了新思路。

参考文献

[1]张鹏飞,程伟,赵煜.考虑耦合效应的动量轮扰动测量[J].北京航空航天大学学报,2011,37(8):948-952.

Zhang Pengfei, Cheng Wei, Zhao Yu. Measure of reaction wheels disturbance considering coupling effect [J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(8):948-952. (in Chinese)

[2]徐赵东,翁沉卉,朱俊涛.航天器中反作用轮干扰力仿真研究[J].振动、测试与诊断,2013,33(5):881-885.

Xu Zhaodong, Weng Chenhui, Zhu Juntao. Method for reaction wheel assembly simulation on spacecraft [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(5):881-885. (in Chinese)

[3]Luo Qing, Li Dongxu, Zhou Weiyong, et al. Dynamic modelling and observation of micro-vibrations generated by a single gimbal control moment gyro [J]. Journal of Sound and Vibration, 2013, 332(19): 4496-4516.

[4]Chen Jiangpan, Cheng Wei, Han Wei. Analysis and simulation of stepper motor disturbance considering structural coupling [C]∥2013 International Conference on Mechanical Engineering and Instrumentation (ICMEI 2013). Brisbane, Australia, Switzerland: Trans Tech Publications, 2014(526):103-108.

[5]程啟华,李永新.压电传感器低频动态补偿数字滤波器设计[J].电子测量技术,2007,30(8):143-146.

Cheng Qihua, Li Yongxin. Design for low-frequency compensation of piezoelectric sensor based on digital filter [J]. Electronic Measurement Technology, 2007, 30(8): 143-146. (in Chinese)

[6]刘向阳,张平,韩振海.动态补偿法在压电传感器静态校准中的应用[J].仪器仪表学报,2004,25(4):9-10.

Liu Xiangyang, Zhang Ping, Han Zhenhai. Application of dynamic compensation method to static calibration of piezoelectric sensors [J]. Chinese Journal of Scientific Instrument, 2004, 25(4): 9-10. (in Chinese)

[7]高全芹.压电传感器动态特性数字化补偿方法应用研究[J].压电与声光,2012,34(4):557-560.

Gao Quanqin. Study on digital compensation method for the dynamics of piezoelectric sensors [J]. Piezoelectrics & Acoustooptics, 2012, 34(4): 557-560. (in Chinese)

[8]贾伯年,俞朴,宋爱国.传感器技术[M].南京:东南大学出版社,2007：144-148.

[9]朱蕴璞,孔德仁,王芳.传感器原理及应用[M].北京:国防工业出版社,2005：77-100.

[10]潘雪涛,温秀兰.传感器原理与检测技术[M].北京:国防工业出版社,2011：171-198.

[11]宋爱国,刘文波,王爱民.测试信号分析与处理[M].北京:机械工业出版社,2007：21-30.

[12]刘向阳,张平,韩振海,等.压电传感器时间常数辨识方法研究[J].仪器仪表学报,2006,27(6):1667-1668.

Liu Xiangyang, Zhang Ping, Han Zhenhai, et al. Research on the identification algorithm for time constant of piezoelectric sensor [J]. Chinese Journal of Scientific Instrument, 2006, 27(6): 1667-1668. (in Chinese)

doi:10.16450/j.cnki.issn.1004-6801.2016.02.019

收稿日期：①2014-03-30；修回日期：2014-07-23

中图分类号TB93； V416.8; TH86

第一作者简介：陈江攀，男，1988年4月生，博士生。主要研究方向为航天器活动部件的微振动特性、微振动信号测试与处理以及结构动力学。曾发表《一种应变式超低频微振动测试台》(《振动与冲击》 2014年第33卷第24期)等论文。E-mail:chenjiangpan@hotmail.com