变式教学美轮美奂

李云凤

变式教学研究是中学数学教学中的一种重要教学策略，变式教学在提高学生的数学学习兴趣、培养学生的数学思维和解题能力等方面有着不可忽视的作用.特别是在初中数学复习过程中，变式教学能使数学知识系统化、条理化，并能促进学生高效地完成数学知识的建构.现将我在教学实践中的几种主要方法展示如下.

一、一题多解，培养发散思维

一题多解就是从不同的角度分析同一问题中的已知条件，运用所学知识把条件和结论链接起来，用不同的解法得到相同结果的思维过程.在复习过程中安排多解题，既可以加深学生对所学各知识点的理解，还有利于学生把握知识点之间的内在联系，掌握各部分知识之间的相互转化方法.

一题多解可以拓宽学生的视野，激发学生的求知欲，满足不同层次学生的需求，从而提高课堂教学效率. 比如在复习利用直角三角形求线段长的时候，我设计了这样的问题，收到了良好的效果.

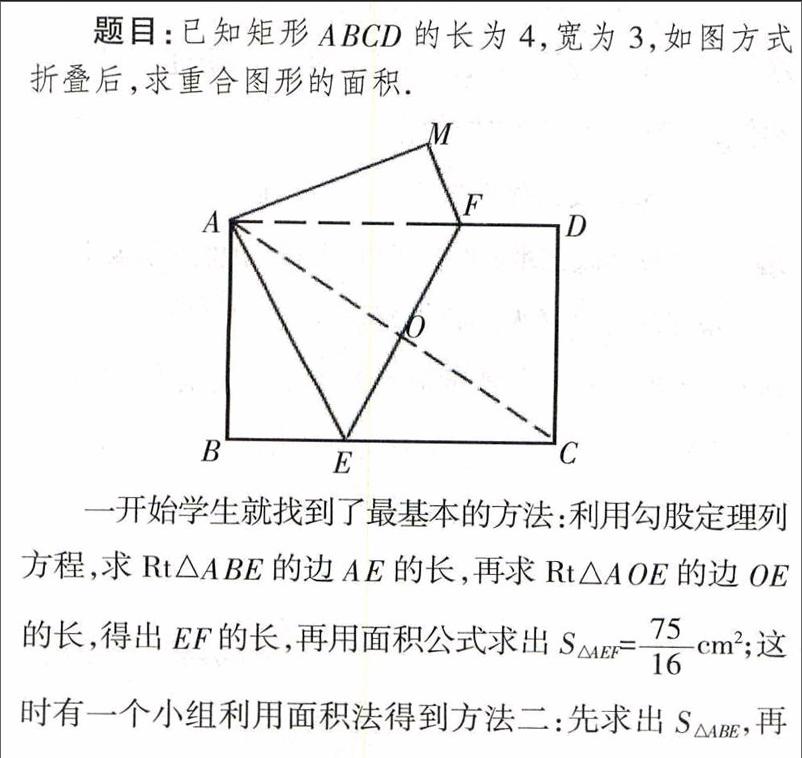
题目：已知矩形ABCD的长为4，宽为3，如图方式折叠后，求重合图形的面积.

一开始学生就找到了最基本的方法：利用勾股定理列方程，求Rt△ABE的边AE的长，再求Rt△AOE的边OE的长，得出EF的长，再用面积公式求出S△AEF=cm2；这时有一个小组利用面积法得到方法二：先求出S△ABE，再利用S△AEF=S矩形ABCD-S△ABE ，不需要求折痕，直接求面积. 至此，学生的思维陷入了僵局，再也没有新方法了. 这时我提出问题：折叠后的图形中，△AEF的面积选用的底和高还可以是谁？引发学生的思考.学生经过讨论发现，底和高还可以选择EF和AO，利用图中的相似形，可以列比例式求线段长.这就是方法三：用相似，即找到Rt△AFO∽Rt△CAB，利用对应边成比例求出OF的长，再根据EF=2OF得出EF的长，再求面积；类似于方法三求EF时，还有同学是这样做的：过F点作FM⊥BC于M，利用Rt△FEM∽Rt△CAB，利用对应边的比直接求出EF的长为，进而求出面积.

回顾这节课，学生的思维得到充分发散.在小结阶段，学生纷纷感慨：一题多解可以让他们从不同角度、不同侧面去分析问题、解决问题，对于利用勾股定理和相似求直角三角形的边长的方法有了更深刻的理解.

二、多题一法，渗透转化思想

初三复习时间短，内容多，怎样高效地整合知识点，使学生在头脑中尽快形成具有个性化的知识体系呢？在教学中，我们要善于以典型例题或习题为源头，将其变式成不同形态的同类型习题，并把它们集中在一起，从不同角度促使学生形成一个共同的认知体系，变单一的知识点考查为多角度多层次的考查，从而使学生对一题的解答能产生解决一类题的效果，即举一反三.

比如，在复习《不等式组的应用》的时候，我设计了这样一组习题：

原题：已知关于x的方程3x-3（a-1）=5x+（2a+1）的解是非负数，求a的取值范围.

变式1：已知关于x的方程3x-（2a-3）x=3的解是非正数，求a的取值范围.

变式2：已知关于x的不等式组6-4x>0， x-a>0的整数解共有4个，求a的取值范围.

题组中把方程和不等式的知识互相结合，既是对方程和不等式的解法的巩固，又通过进一步将知识内化，从而获得解决此类问题的方法：类比想象，学生将不等式的问题转化为解含字母系数的方程和不等式，再根据题意列不等式，进而求解.

再比如：利用尺规作图法解决已知两固定点A和B来寻找等腰三角形的第三个顶点C的方法：即分别以A、B为圆心，以AB长为半径做圆，与固定直线的交点为点C.或做AB的垂直平分线，与固定直线的交点为点C.这些方法是解决这一类问题时的通法.下面这个问题却是寻找菱形的第四个点，它和等腰三角形有什么关系呢？

题目：如上图所示：已知点M在直线BQ：y=-2x+12上，问：在平面直角坐标系中是否存在一点N，使以点M、D（4，0）、B（6，0）、N为顶点的四边形为菱形？若存在，请直接写出N点坐标，若不存在，请说明理由.

由于在菱形的四个点中，D、B为已知点，点M在直线BQ上，N随M的变化而变化，根据菱形四边相等的性质可以发现，三角形DBM必为等腰三角形，从而将问题化归为已知点B和点D，寻找等腰三角形第三个顶点M的问题，进而构造菱形，找到相应的N点.将菱形的存在性问题转化为等腰三角形的存在性问题，可使学生深刻认识到转化的重要意义.

三、一题多变，开拓思维

利用全等三角形证明线段相等和角相等是牡丹江中考数学压轴题.如何在复习的过程中让不同层次的学生有不同的收获呢？在教学中我发现：这类图形的证明基本是利用图形的三大运动变换进行的图形变式，虽然图形发生了变化，但解决问题的核心知识点却是一致的，即“图变法不变”.让不同层次的学生均能下手尝试，从而积极寻求解题的规律和方法.

下面我以2009年牡丹江市中考数学试卷第26题的第3个图为蓝本，阐述我在题目设计上的尝试：

以右上图为基本图形，我发现：若原题目图形不变，在等腰直角三角形内部作一个以AC为斜边的直角三角形，使点P恰好落在一条直角边上，那么图中以P为端点的三条线段PC、PD、PA有一定的和差关系.

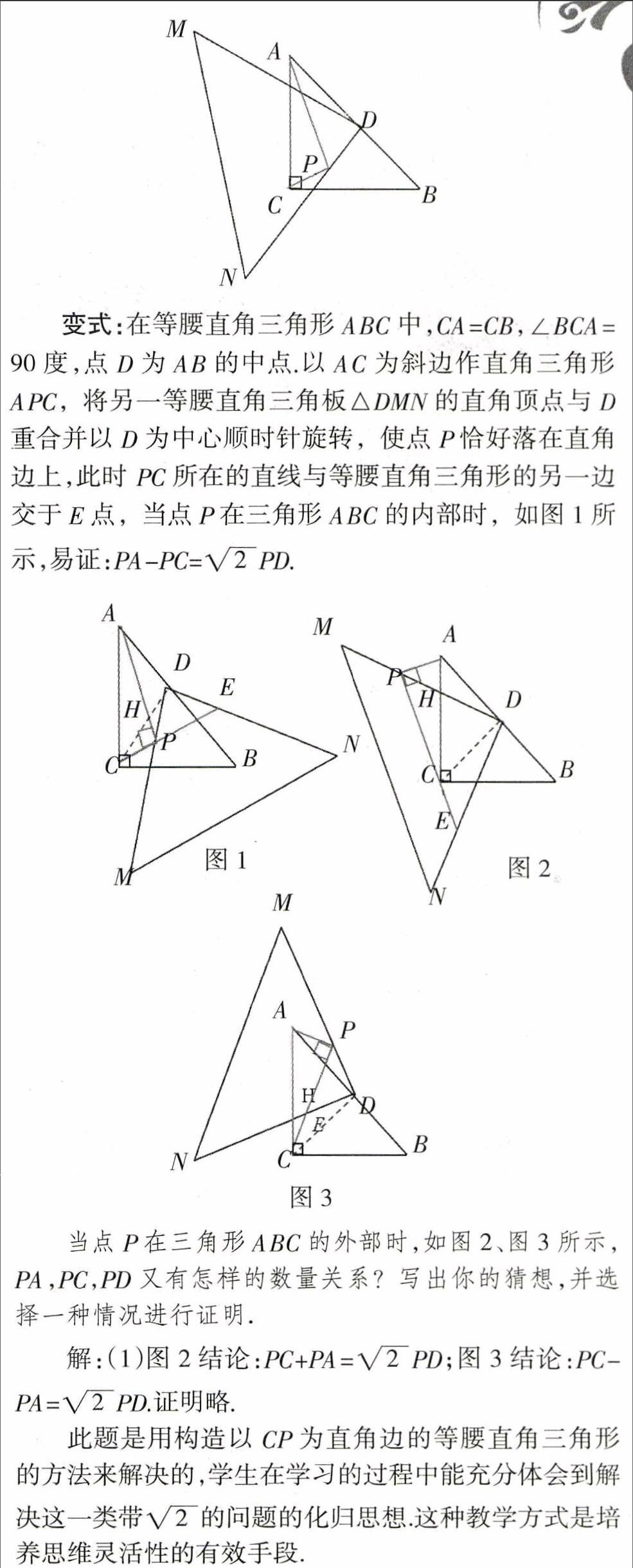
变式：在等腰直角三角形ABC中，CA=CB，∠BCA=90度，点D为AB的中点.以AC为斜边作直角三角形APC，将另一等腰直角三角板△DMN的直角顶点与D重合并以D为中心顺时针旋转，使点P恰好落在直角边上，此时 PC所在的直线与等腰直角三角形的另一边交于E点，当点P在三角形ABC的内部时，如图1所示，易证：PA-PC=PD.

当点P在三角形ABC的外部时，如图2、图3所示，PA，PC，PD又有怎样的数量关系？写出你的猜想，并选择一种情况进行证明.

此题是用构造以CP为直角边的等腰直角三角形的方法来解决的，学生在学习的过程中能充分体会到解决这一类带的问题的化归思想.这种教学方式是培养思维灵活性的有效手段.

变式教学的实施，极大地提高了我的教学水平和编题视野，我不必再沉浸于题海战术，而是利用深挖课本例题、中考题，并将其充分演变，促使学生通过问题的表象看到问题的本质，引领学生举一反三、触类旁通.