一种基于可学习快速回归量的稀疏编码算法

黄会群

（湖南财政经济学院信息管理系，湖南长沙　410205）



一种基于可学习快速回归量的稀疏编码算法

黄会群

（湖南财政经济学院信息管理系，湖南长沙410205）

摘要：针对现有的稀疏编码和建模算法计算量太大的问题，文章基于可学习快速回归量来精确近似稀疏码这一思路，提出了全面的结构性稀疏编码和建模算法.首先根据分块坐标算法的迭代，提出一种高效的前馈架构.该架构可以精确近似结构性稀疏码，且复杂性远远低于标准优化算法.其次证明了通过使用不同的训练目标函数，得出的可学习稀疏编码器不仅可以近似给定字典条件下的稀疏码，还可用作全功能稀疏编码器及建模工具.仿真实验结果表明，与当前最新的精确优化算法相比，文中算法的性能基本相当，但运行速度快出数个数量级，更加适用于实时和大规模应用领域.

关键词：稀疏编码；建模；快速回归量；算法

0　引言

稀疏编码［1］是指将信号表示为给定字典基本原子的一个稀疏线性组合.稀疏建模主要是根据数据本身对（非）参数字典进行学习.除了在理论层面引起人们大量研究兴趣外，该模型还对许多信号进行了有效描述，从多种应用领域中的大量最新应用成果［2-3］中可以看出这一点.

文献［4］提出了一种基于K近邻稀疏编码均值约束的人脸超分辨率算法.首先根据人脸块位置先验信息，基于聚类得到与输入人脸图像块位置一致的高、低分辨率稀疏表示字典对；然后在稀疏和K近邻稀疏编码均值的共同约束下通过系数映射实现图像块的精确重建.文献［5］将结构相似度引入到稀疏编码模型中，提出基于结构相似度的稀疏编码模型.基于该模型提取出图像的稀疏编码特征.实验结果表明，改进后的稀疏编码模型更好地保持了结构信息，更加符合人眼视觉系统特性.将文中提出的稀疏模型应用到特征提取中，可获得结构信息保持得更好的图像特征.文献［6］提出了稀疏字典编码的超分辨率模型，将高、低分辨率图像特征块统一进行稀疏编码，建立高、低分辨率图像的稀疏关联，同步实现匹配搜索和优化估计，突破了基于学习方法的限制.然后，应用形态分量分析法提取图像的特征数据，提高了特征匹配的精确性，并同步实现了超分辨率重建和降噪功能.最后的仿真实验结果表明，与其他基于学习的超分辨率算法相比，该模型重建得到的图像质量更优.

然而，所有基于优化的稀疏编码和建模算法，其主要问题是计算量太大.因此，人们投入大量精力研究高效的优化算法［7-8］.虽然许多文献取得了持续进步，但是当前最新算法仍然需要数千次的迭代才能收敛，因此无法用于实时或大规模应用场合.最近有人在研究中提出，通过学习在规定时间内可以有效近似稀疏码的非线性回归量，以牺牲稀疏表示的精度为代价来换取计算速度的提高［9］.文献［10］提出了一种新的算法，该算法的回归量为多层人工神经网络（NN），且神经网络的结构受到稀疏编码优化算法的启发.这些回归量经过训练后，可以实现给定训练集的预测码和精确码间MSE最小化.另外，由于该算法在推导过程中允许近似“解释”，所以可对真实稀疏码进行更精确的近似.本文对文献［10］的研究工作进行了扩展，考虑了更加普通的稀疏编码范例（分组和非重叠分组），底层字典/模型的在线更新，因此大大增加了快速编码算法的可用性.本文算法可用于预先明确的字典，也可以对供应给它的相同的数据向量进行在线学习，因此更加适用于实时和大规模应用领域.

本文的组织结构如下：第2节简要描述分层结构性稀疏码，第3节讨论用于编码器架构的优化算法，第4节给出新的稀疏编码器及训练时使用的新的目标函数，第5节给出基于真实音频和图像分析的实验结果，第6节做总结.

1　结构性稀疏模型

稀疏模型的底层假设是，输入向量可以被精确重构为带有少量非0系数的部分（往往是经过学习的）基本向量（因子或者是字典原子）的线性组合.结构性稀疏模型进一步假设，非0系数模式具有特定的先验结构.

设D∈ℜm×p为带有p个m维原子的字典.本文根据它们的索引来定义原子群组G⊆｛｝1，…，p.然后，我们将群结构ς定义为原子群组的集合，且.对输入向量x∈ℜm，与群结构ς相关的对应的结构性稀疏码z∈ℜp，可以通过求解凸规划获得：

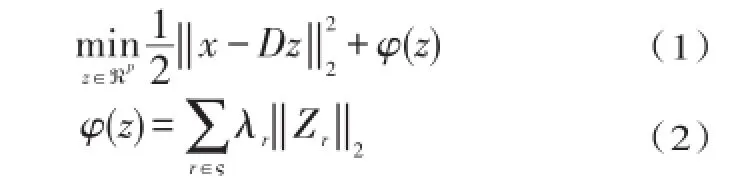
其中，向量 zr∈ℜ||Gr包括属于组r的z的系数，λr是控制稀疏度的标量权重.

式（1）中的正规化函数φ可以看成是标准稀疏编码使用的ℓ1正则器的泛化，而后者来自单群组且λr=1这一特殊情况.同样地，它对z群组的影响也是对通过标准稀疏编码获得的正则器的一种自然泛化：它根据ς施加的结构，“打开”或“关闭”群组中的原子.

几种重要的结构性稀疏设置可被看成是式（1）中的具体情况：（1）稀疏编码［11］，主要是指Lasso或基逼近（basis pursuit）；（2）群组稀疏编码，标准稀疏编码的一种泛化，此时字典被细分为同时处于活跃或非活跃状态的多个群组［12］，这种情况下的ς为｛｝1，…，p的一种分割；（3）分层稀疏编码，假设非0系数具有分层结构［13］.群组ς根据包含关系（树结构）形成一个层次；也就是说，如果两个群组重叠，则其中一个完全包含于另外一个；（4）协作式稀疏编码，通过推广系数矩阵非0元素的给定模式，将结构性稀疏编码概念提炼为输入向量集合［13］.

2　优化算法

当前求解式（1）的最新算法主要依赖近端分裂算法系列［14］.下面，我们简要介绍了近端分裂算法和分层稀疏编码问题的求解算法，该算法将被用于构建可训练稀疏编码器.

2.1正向-反向分割

正向-反向分裂算法主要用于求解无约束优化问题，其成本函数可被分裂为：-Lipschitz连续梯度；f2是凸、扩充、实值函数，可能为非平滑函数.考虑到

其中，f1是凸、可微函数，具有且f2（z）=φ（z），问题（1）显然属于这一类别.固定步骤的正向-反向分裂算法定义了一系列循环：

算法1：正向-反向分割算法

输入：数据x，字典D，正则器φ

输出：稀疏码z

4.until收敛为止

因为近端算子φ可以精确、高效地计算出来（比如利用标准或群组结构性稀疏编码），正向-反向算法变得非常有趣.当ς群组随机重叠时，没有一种方法可以直接高效地做到这一点.然而，也存在一些比较重要的例外情况，比如将在下文讨论的具有树结构群组的分层设置.文献［7］对加速近端算法进行了广泛研究，以提高它们的收敛速度.虽然目前从理论和实践角度来说，这些算法是可用的速度最快的精确求解算法，但是它们仍然需要上千次的迭代才能收敛.由于本文研究的目的是为稀疏编码器创建一个架构，所以将在下一节对算法标准版本展开详细讨论.

2.2近端算子

为了对标记法进行简化，我们将在下文中对双层稀疏编码时的推导过程加以阐述，并称为HiLasso模型［13］.引入HiLasso模型是为了同时促进群组和系数水平上的稀疏性.给定一种分割，群组结构ς可表示为两种分割的并集：p和单群组集合.因此，正则器φ为：

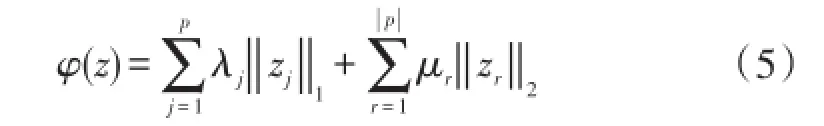
然后，φ近端算子可按封闭型计算出来.给定索引群组的一种分割p及阈值参数向量，当时，本文定义群组可分离算子（r=1，…，||p）为：

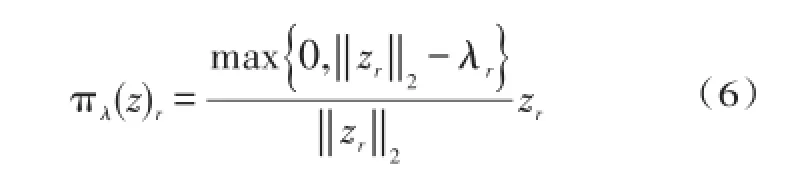
否则为0.注意，πλ为p中的每一个群组使用了一个向量软阈值约束.式（5）中的近邻算子可被表示为：

它合成了与ς中每种分割相关联的近端算子：p和单群组集合.Lasso问题是HiLassoμ=0且λ=λ1时的特殊情况，此时式（7）中的近端算子转化为标量软阈值算子，且算法1对应于常见的迭代收缩和阈值算法（ISTA）［7］.

2.3分块坐标正向-反向算法

算法1每次迭代时需要根据式（7）对分割p中的所有系数群组进行更新.我们可以选择分块坐标策略，每次只对一块进行更新.本文将这种算法称为分块坐标正向-反向算法（BCoFB）.BCoFB的迭代内容如下：

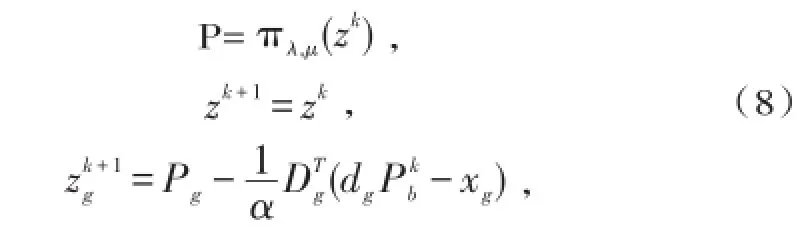
其中，1/α是拟合项的Lipshitz常数，g是第k次迭代将被更新的p中群组的索引.文献［15］为标准稀疏编码引入了坐标下降算法（CoD），受该算法启发，本文提出了一种探索式BCoFB算法，对群组进行更新：

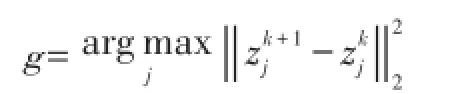
可以看出，该等式为所有可能的群组更新成本函数的下降提出了一个下限.具体步骤见算法2.

算法2：BCoFB算法

输入：数据x，结构性字典D，λ，μ

输出：结构性稀疏码z

3.初始化z=0，b=Wx

5.until收敛为止

3　快速结构性稀疏编码器

为了让实时环境可以应用稀疏编码，人们最近提出可以在规定时间内生成稀疏码精确近似的回归量［9］，其主要思路是创建带有某组参数（共同表示为Θ）的参数回归量h（x，Θ），以实现成本函数在训练集｛｝x1，…，xN上最小化：

正常情况下，除了学习之外，我们还可以简单地根据CoD算法设置参数S、W和t（算法2的特定情况），然后在少量次数的循环后终止.然而，这丝毫无法保证，修剪版的CoD算法在相同（较少）数量的层次后，生成的稀疏码近似最优.不经过学习，这一修剪版本的近似往往毫无用处.另外，即使是对参数进行学习，我们也无法期望神经网络回归量对任意输入数据均能生成高质量的稀疏码.但是，文献［10］证明了，如果输入向量的分布与训练集使用分布相同，则神经网络可以生成高质量的稀疏码近似.

ISTA和CoD稀疏编码器架构的另一个显著特性是：它们关于参数和输入殆遍连续（c1）.由于关于参数可微，所以可以使用（子）梯度下降算法进行训练；由于关于输入可微，因此支持梯度的反向传播，并可在更大规模的全局训练系统中将稀疏编码器作为一个模块加以应用.

损失函数τ（Θ）关于Θ的最小化需要计算（子）梯度dτ（Θ，xn）/dΘ，这可以通过反射传播步骤实现.反射传播首先用上一网络层的输出对τ（Θ，xn）求微分，然后将（子）梯度向下传播给输入层，将其与被穿越层的雅可比矩阵相乘.

3.1层稀疏编码器

本文将文献［10］的思想扩展到分层（结构性）稀疏码回归量中.我们考虑基于BCoFB的前馈架构，每层实施BCoFB近端算法（算法2）的一次循环.本质上每一层由非线性近端算子πs，t、群组选择器及与该组对应的线性操作Sg构成.网络参数根据算法2初始化. 当α=1且s=0时，可以获得CoD架构.

3.2另一种训练目标函数

迄今，我们根据文献［10］的思想，将神经网络用作回归量，其唯一作用就是尽可能精确地重建迭代稀疏编码算法（比如Lasso或HiLasso算法）生成的理想稀疏码.实现方法是对网络进行训练，以尽量减小

间的差ℓ2.我们没有把神经网络稀疏码（结构性和非结构性）看成近似某种迭代算法的回归量，而是根据它的特点将其看成全功能稀疏编码器（甚至是建模工具）.为了实现这种思路上的转变，我们丢弃理想的稀疏码，并引入另一种训练目标，具体内容在下文详细描述.

一般的稀疏编码问题都可看成是数据向量x和对应的稀疏码z间的映射，以实现拟合项和（可能情况下的结构性）正则器之和（即最小化.由于后一目标被认为是编码质量指示器，我们可以对网络进行训练，以尽量减小f在训练集上的总体均值，此时用z=h（x，Θ）替换z=argminf（x，z），获得的目标函数为：

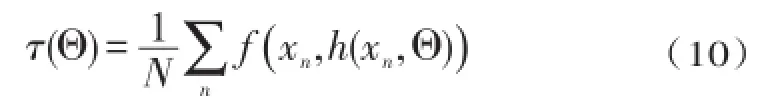
确定完应用领域后，我们需要选择一个目标函数，且正则器φ与问题结构相对应，稀疏编码器架构与该结构要匹配，然后对后者进行训练，以实现目标函数在代表性的一组数据向量上最小化.我们发现，选择的稀疏编码器的结构是否与训练目标及问题的内在结构相匹配，对能否生成高质量的稀疏码具有极其重要的作用.

因为基于神经网络的稀疏编码器是通过实现非凸函数在训练集上最小化来进行训练，因此容易出现局部收敛和过拟合问题，所以我们认为，在大部分实际问题中，根据代表性的数据分布求解非凸字典也可以确定字典D.因此，除非根据一些领域知识构建字典，否则使用神经网络稀疏编码器与使用迭代式稀疏建模算法在概念上没有区别.

此外，我们可以把字典看成是训练时的另一个优化参数，然后关于D及网络参数Θ对τ最小化，在网络训练和字典更新迭代间来回交替.这在本质上将本文高效的稀疏编码技术拓展到全功能稀疏建模领域，具体内容在下文详细讨论.

3.3在线学习

将神经网络看成是独立的稀疏编码器，然后抛弃精确的参考稀疏码，这会导致训练问题完全成为一个无监测训练问题.因此，我们可以使用稀疏编码时提供给它的相同的数据向量，对网络进行训练（也有可能对字典进行调整）.这允许我们在在线学习领域使用本文算法.一个完整的在线稀疏建模场景由以下要素组成：（1）字典初始化（比如根据初步观察到的训练数据向量构成的随机样本），（2）固定训练目标中的字典，利用在线学习算法根据新到的数据对网络参数进行调整（本文小批量使用在线随机梯度算法，具体内容见第5节），（3）固定稀疏码，根据在线字典学习算法来调整字典.请注意，以上所有步骤完全不需要循环稀疏编码，因此大大降低了延时和计算量，支持实时应用.

3.4有监督有差别学习

本文提出的稀疏建模技术可以自然地合并训练数据向量的次要信息，使得学习成为有监督学习.鉴于篇幅有限，我们不对此进行详细探讨，下面将简要描述几个例子.

（1）对群组或分层Lasso情况，我们可能知道我们希望获得的每个数据向量的活跃群组.将这一信息纳入训练目标可以通过如下方法实现：根据式（5）利用τ，为每个训练向量xn单独设置 μr，若要提高已经激活的群组r的活跃度则将其设为较小值，若要防止未激活群组被激活则将其设为较大值.

（2）在其他应用情况下，数据向量可按成对的已知类似或互异向量呈现，我们可能希望实现类似向量稀疏码自然距离最小化的同时，实现互异向量距离的最大化.这一情况在检索应用中非常有趣，此时由于它们对高效检索的支持性，人们非常希望获得稀疏数据表示.在指标学习时经常将这一相似度保存项纳入训练目标中，但是在稀疏编码时这一做法很有难度，原因如下：当迭代算法生成稀疏码时，我们将面临根据另一目标f对训练目标τ最小化这一问题.如果我们使用神经网络稀疏建模工具，则可以依托标准算法处理训练问题.

（3）最后，许多应用的数据没有欧几里德结构，我们可以使用有监督学习来构建最优区分性指标.比如，这可以通过如下方法实现：用Mahalanobis拟合项替换欧几里德拟合项，且，其中Q是区分性投影矩阵.此时，我们希望将稀疏建模与指标学习结合起来.这一问题在之前还未被考虑过，原因是当通过f最小化获得稀疏码时，考虑稀疏建模与指标学习的结合问题并不现实.

4　实验结果

实验环境设置为：所有神经网络部署在带有GPU加速组件的Matlab平台上，运行条件为最新的Intel Xeon E5620 CPUNVIDIA Tesla C2070 GPU.此时的稀疏码绝非最优，105个100维向量在10层结构性网络上基于本文BCoFB架构的传播，只需要3.6秒，相当于每层每个向量3.6微秒.这比运行于CPU上的极其优化的多线程SPAMS HiLasso码要快出数个数量级［16］.之所以取得这样的并行化效果，是因为固定了数据路径，神经网络编码器的复杂度低于迭代算法.

所有实验的训练均基于Armijo准则条件下的梯度下降算法.我们将通过文献［10］的目标函数（精确编码器输出的ℓ2误差）最小化获得的神经网络稀疏编码器称为NN G-L.

4.1分类

在实验中，我们以MNIST数码分类任务为依托，对非结构性神经网络稀疏编码器进行性能评估. MNIST图片被重新采样为17×17（289-维）区域.每个类别对一组10个字典进行训练.分类实验时，为每个字典的测试向量进行编码，然后根据完整的Lasso目标最小值来分配类别.

对以下稀疏编码器进行比较：精确稀疏码（精确Lasso码），非结构性NN G-L码，非结构性NN Lasso码（基于Lasso目标进行训练的CoD网络）.训练10个网络，每个类别1个网络，每个包括T=5个CoD层.设置Lasso目标的λ=0.1.使用的字典有100个（不完全）和289（完全）个原子.字典规模进一步增大并不能显著提升性能.

表1总结了每个稀疏编码器的错分率.当字典规模变大时，NN G-L稀疏编码器的性能将会下降，但与精确编码的差异也会下降.另一方面，Lasso目标函数的性能越好，正确分类率越高，因此更宜选择NN Lasso.NN Lasso编码器训练时对字典进行调整，只会轻微提升性能，且会随着字典规模的上升而下降.本文认为主要原因是数据的复杂度相对较低.

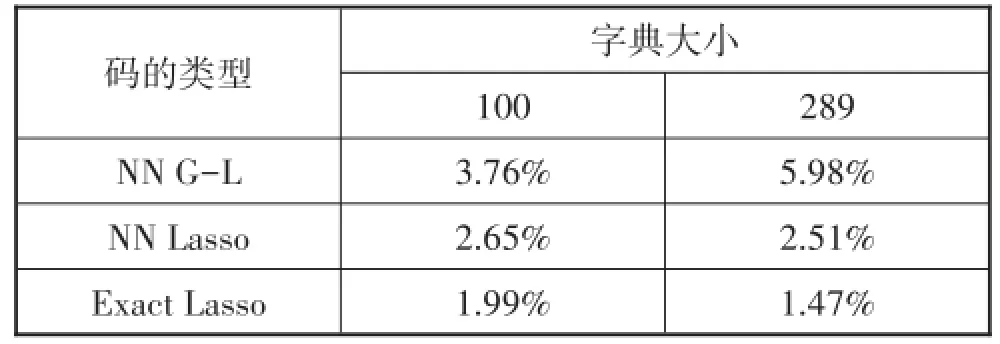
表1　MNIST数码的错分率

4.2结构性编码

本节根据文献［13］重现扬声器识别任务，进而评估结构性稀疏编码器的性能.在该应用中，文献［13］使用HiLasso及已知的固定信号来自动检测当前扬声器.本文则使用提出的结构性稀疏编码器来重复这一实验.

数据集包括5种不同扬声器录音，2位女性，3位男性.25%的样本用于训练，其余用于测试.对测试数据，创建两组波形：一组包含各个单独的扬声器，另一组包含2个扬声器各种可能的组合.信号被分解为一组重叠率为75%的带有512个样本的重叠局部时间帧，以便信号特性在每个帧中保持稳定.每个音频帧获得一个80维特征向量作为它的短时功率谱包络（见文献［13］）获得更多细节）.5个不完备字典（50个原子）基于单扬声器集合进行训练，以实现Lasso目标最小化且λ=0.2（每个扬声器一个字典），然后综合为包含250个原子的一个结构性字典.首先对结构性字典中的测试向量进行编码，然后对5个群组测量每个群组的ℓ2能量.500个时间样本的能量放在一起求和，进而选择排名最高的2个类别.

与以下结构性稀疏编码器做比较：μ=0.05的精确HiLasso码（Exact）编码器，基于精确HiLasso码进行训练的非结构性NN G-L（NN G-L unstructured）编码器，基于相同码进行训练的结构性NN G-L（NN G-L structured）编码器，支持区分性成本函数（带有正规化项）的结构性网络编码器，此时，对每个数据向量，权重μr独立设为-1或1，以根据扬声器的活跃或静止情况，促进或防止对应群组的激活（NN discriminative structured）.所有神经网络使用相同的信号结构性字典，且带有T=2层BCoFB架构.

表2总结了错分率情况.很显然，即使层次数量和字典相同，相对非结构性算法，结构性算法的性能可以提升2倍.使用区分性目标函数也可以提升性能.但是，使用只有两层的神经网络后，正确分类率只下降了1%.

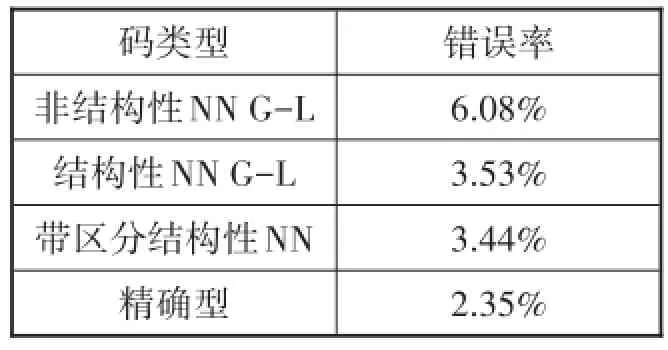
表2　音频数据集的错分率

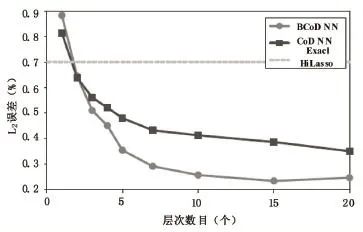
图1　基于结构性稀疏合成数据的结构性和非结构性神经网络性能（ℓ2误差）

结构性架构对生成精确的结构性稀疏码具有重要作用.本文现在验证，在普通情况下仍然可以观察到这一现象.我们按照前述条件重复了这一实验，但是使用了随机生成的合成数据，合成数据在给定字典（神经网络未知）后具有结构性稀疏表示，实验结果见图1.可以看到，随着层数的增加，除了精确HiLasso编码器的ℓ2误差保持不变外，另外两种方法的ℓ2误差都随着层数的增加而降低，其中BCoD NN的ℓ2误差最低.这也表明了本文提出的结构性稀疏编码器的有效性.

5　结论

本文利用了多层神经网络的凸优化思想，针对实时和大规模应用领域，提出了一种全面的稀疏编码及建模方法.内容包括不同的目标函数参与重建和分类，支持分层和群组相似度等不同的稀疏编码结构，同时可应用于在线学习领域.与当前其他最新算法相比，本文算法简单部署后虽然性能有轻微下降，但将速度提高了数个数量级，证明了稀疏建模可在多种应用中取得成功，为实用算法开辟了广阔的前景.我们下一步研究工作的重点是将文中提出的稀疏编码及其几建模方法应用到视频异常检测、图像特征提取等问题中.

［参考文献］

［1］亓晓振，王庆.一种基于稀疏编码的多核学习图像分类方法［J］.电子学报，2012，40（4）：773-779.

［2］杜馨瑜，李永杰，尧德中，等.基于图像导数框架和非负稀疏编码的颜色恒常计算方法［J］.电子学报，2012，40 （1）：179-183.

［3］宋长新，马克，秦川，等.结合稀疏编码和空间约束的红外图像聚类分割研究［J］.物理学报，2013，62（4）：40702-040702.

［4］黄克斌，胡瑞敏，韩镇，等.基于K近邻稀疏编码均值约束的人脸超分辨率算法［J］.计算机科学，2013，40（5）：271-273.

［5］李志清，施智平，李志欣，等.结构相似度稀疏编码及其图像特征提取［J］.模式识别与人工智能，2010，23（1）：12-19.

［6］李民，程建，乐翔，等.稀疏字典编码的超分辨率重建［J］.Journal of Software，2012，23（5）：1315-1324.

［7］Beck A，Teboulle M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems［J］.SIAM Journal on Imaging Sciences，2009，2（1）：183-202.

［8］Xiang Z J，Xu H，Ramadge P J.Learning sparse representations of high dimensional data on large scale dictionaries［C］. Advances in Neural Information Processing Systems.2011：900-908.

［9］Kavukcuoglu K，Ranzato M A，LeCun Y.Fast inference in sparse coding algorithms with applications to object recognition［J］.arXiv preprint arXiv：1010.3467，2010.

［10］Gregor K，LeCun Y.Learning fast approximations of sparse coding［C］.Proceedings of the 27th International Conference on Machine Learning（ICML-10）.2010：399-406.

［11］Mota J F C，Xavier J M F，Aguiar P M Q，et al.Distributed basis pursuit［J］.Signal Processing，IEEE Transactions on，2012，60（4）：1942-1956.

［12］Yuan M，Lin Y.Model selection and estimation in regression with grouped variables［J］.Journal of the Royal Statistical Society：Series B（Statistical Methodology），2006，68（1）：49-67.

［13］Sprechmann P，Ramirez I，Sapiro G，et al.C-HiLasso：A collaborative hierarchical sparse modeling framework［J］. Signal Processing，IEEE Transactions on，2011，59（9）：4183-4198.

［14］Bach F，Jenatton R，Mairal J，et al.Convex optimization with sparsity-inducing norms［J］.Optimization for Machine Learning，2011：19-53.

［15］Li Y，Osher S.Coordinate descent optimization for ℓ 1 minimization with application to compressed sensing；a greedy algorithm［J］.Inverse Probl.Imaging，2009，3（3）：487-503.

［16］Jenatton R.Mairal J.Obozinski G.and Bach F.Proximal methods for hierarchical sparse coding［J］.JMLR，2011，12 （5）：2297-2334.

（责任编辑：李洁坤）

中图分类号：TP391

文献标识码：A

文章编号：2096-2126（2016）03-0128-06

［收稿日期］2016-03-10

［基金项目］2015年湖南省十二五教学科学规划立项项目“慕课采纳影响因素及发展策略研究”（XJK015CGD008）和2015年湖南省普通高等学校教学改革研究立项项目“在线开放课程的使用影响因素及预测研究”（15XJT291-593）阶段性成果之一。

［作者简介］黄会群（1976—），男，湖南蓝山人，博士在读，讲师，研究方向：数据挖掘、综合评价及应用、教育技术采纳。

An Sparse Coding Algorithm Based on the Learnable Fast Regressors

HUANG Huiqun

（The Department of Information Management，Hunan University of Finance and Economics，Changsha，Hunan，410205 China）

Abstract:Aiming at the higher computation in existing sparse coding and modeling algorithms，we present a comprehensive frame⁃work for structured sparse coding and modeling extending the recent ideas of using learnable fast regressors to approximate exact sparse codes.First of all，we propose an efficient feed forward architecture derived from the iteration of the block-coordinate algorithm.This ar⁃chitecture approximates the exact structured sparse codes with a fraction of the complexity of the standard optimization methods.We also show that by using different training objective functions，the proposed learnable sparse encoders are not only restricted to be approximants of the exact sparse code for a pre-given dictionary，but can be rather used as full-featured sparse encoders or even modelers.The simula⁃tion results show that several orders of magnitude speedup compared to the state-of-the-art exact optimization algorithms at minimal per⁃formance degradation，making the proposed framework suitable for real time and large-scale applications.

Key words:sparse coding；modeling；fast regressors；algorithm