基于熵的应急物流网络稳定性研究

赵 静 娴

(天津科技大学 经济管理学院，天津 300222)



基于熵的应急物流网络稳定性研究

赵 静 娴

(天津科技大学 经济管理学院，天津 300222)

摘要：将熵的概念引入应急物流网络稳定性研究领域，提出了基于熵的应急物流网络节点稳定性度量指标，进而给出了应急物流网络整体抗毁性的计算公式，最后通过算例验证了方法的有效性与实用性。

关键词：应急物流；物流网络；网络稳定性；抗毁性；熵

应急物流是指为应对突发自然灾害、公共卫生事件、公共安全事件等而对物资、人员、资金的需求进行紧急保障的一种特殊物流活动。如2003年我国非典疫情引起的物资供应，2008年汶川大地震的救援工作，2011年日本福岛第一核电站因地震损毁严重引起核泄漏导致21万人紧急疏散，2015年天津8·12大爆炸后周边小区的人员紧急疏散及防化救援物资运送，以及战争时期的后勤保障等[1]。随着对应急突发事件管理研究的深入，应急物流也引起了学界的高度关注。应急物流系统是指在突发事件、灾害或战争中对物资、人员、资金、信息进行紧急流通保障的系统，相比于传统的物流系统有其自身突出的特点和特殊的要求，如弱经济性、强时效性、突发性、随机性等，因此，应急物流网络的组织、评价和管理与普通物流网络有较大区别，同时，对物资的载运方式、运输路径、配送方式、流通效率、网络容灾、协调指挥、信息共享等方面也提出了更高的要求。

应急物流网络是应急物流建设中的重要组成部分，目前有关应急物流网络的研究大多集中在多约束条件下的网络构建上[2-3]，然而在实际情况中，自然或人为的突发事件常常会使物流网络遭到局部的破坏，在这种情况下，物流网络能否依然连通确保物资送达受灾地区就显得尤为重要，因此，有必要对应急物流网络的抗毁性进行研究，找到网络中稳定性薄弱的节点加以改进。

一、应急物流网络的稳定性

(一)应急物流网络稳定性的定义

物流网络的建设是物流领域的重要问题，在灾害和战争等条件下，网络的中断就意味着物流体系的功能丧失。普通的物流网络设计和研究主要考虑物流网络的经济性，如流通的速度、流量和效率等，而应急物流网络设计必须将安全性即网络的稳定性放在首位。很多学者对应急物流网络的稳定性给出了定义和解释，如陈坚等[4]提出将应急连通可靠性定义为当自然灾害或突发因素导致系统中某些路段受损时，网络依旧保持连通状态，并仍能持续满足救援物资需求的概率，其中各节点受到灾害影响后依然相互连通的强度反映了网络的抗灾能力和可持续能力。孙君等[5]认为网络的稳定性主要指物流网络遇外界扰动后不受影响、不受破坏或抗干扰的能力，包括节点可靠能力和线路可靠能力两个方面，这两者决定了网络连通可靠性、网络容量可靠性、行程时间可靠性和网络成本可靠性。而网络的稳定性简单地说就是在相同的建网代价下网络抵抗破坏的能力或者说网络抵御破坏的冗余度，应急物流网络的设计就是使用最小的建网代价构建冗余度最高的网络。

(二)应急物流网络稳定性的度量

对于应急物流网络稳定性的度量是评价和设计应急物流网络的基础。孙君等[5]从拓扑角度分析了灾后对地面应急物流网络系统的干扰影响、应急物流网络的可靠能力及应急物流网络的组织办法，但是没有给出具体的网络稳定性度量指标。Bengang Gong等[6]利用模糊熵聚类方法建立了评估应急物流网络可靠性的方法。陈小可[7]同样利用聚类方法但从不同的角度讨论了应急物流网络遭受破坏前后的连通情况，构建了鲁棒性模型，并用实验验证了受到干扰和破坏后稳定鲁棒性和性能鲁棒性的统计变化规律。这些研究主要侧重于应急物流网络对干扰和破坏的变化规律描述。Zhao等[8]引入复杂网络理论，通过路网拓扑结构讨论高速公路的系统抗毁性。Peng等[9]研究了基于级联失效的无标度网络关键节点故障的抗毁性，并在BA网络框架下进行了数值模拟。陈坚等[4]考虑不同灾害程度对路段造成的破坏引入灾害影响系数，描述灾害大小及对路段通行能力的影响程度，但是灾害破坏程度需要专家评估，阈值的设计和指标体系的建立也可能受到人为因素的影响。吴六三等[10]认为应急网络的稳定性根据实际情况需要区分最大流量和最短路径哪个优先的情况，并定义了应急物流网络的最大流熵和最短路熵概念作为度量网络稳定性的指标。然而，在灾害发生时，往往首先需要考虑的是是否存在连接冗余的问题，即网络抵御破坏的能力，其次才是如何使流量最大、路径最短的问题。同时，对于同一问题往往存在最大流和最短路的同步需求，如战时应急后勤网络，迅速充分地满足前线需求是同等重要的要求，而是否在遭受破坏后仍然有补给通路是最基本的要求。因此，最大流熵与最短路熵在度量应急网络的稳定性上存在一定的不足。

二、基于熵的应急物流网络稳定性度量

为了简便准确地度量应急物流网络的稳定性，本文从应急物流网络的拓扑结构出发提出节点稳定性的概念，进而给出了基于熵的应急网络全网整体稳定性的度量指标。

(一)不重叠路径

不重叠路径的定义是：在无向网络图G(A，V)中，其中V=(v1，…，vn)，代表n个城市；A=(a1，…，am)，代表城市间的道路。对于G中的两条链，如果不含有任何相同的边，则称为不重叠路径。

图1为6节点8边网络，其中城市v1到城市v2之间共有4条通路：v1-v2；v1-v6-v3-v2；v1-v6-v5-v2；v1-v6-v5-v3-v2。但其中后3条通路中均含有道路v1-v6，如果该道路出现问题，3条通路将同时瘫痪，因此应将后3条路径视为同一条，城市v1到城市v2之间的不重叠路径数为2。

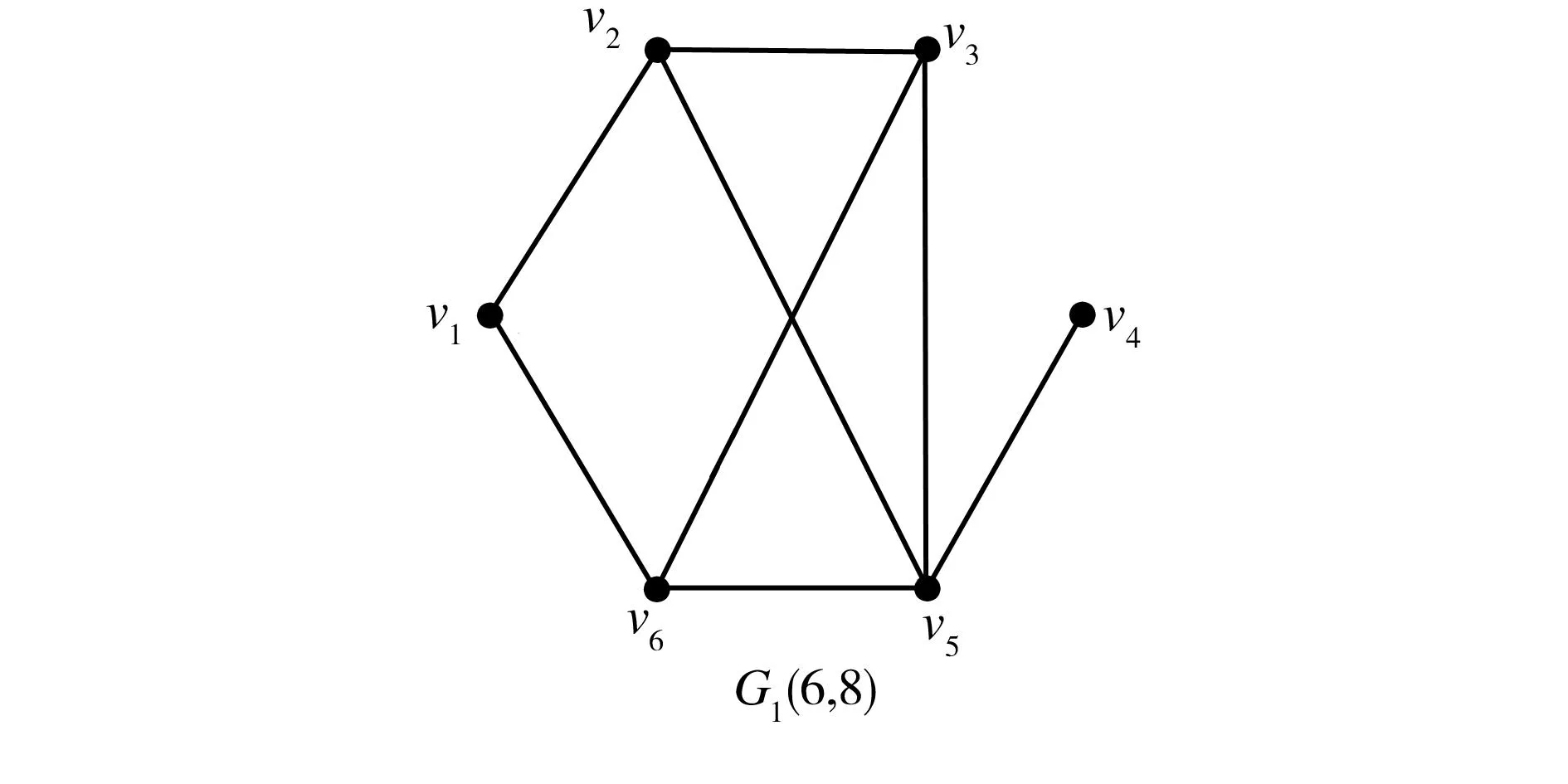
图1　6节点8边网络

(二)基于熵的应急物流网络稳定性评价

熵最早由德国物理学家鲁道夫·克劳修斯提出，用于描述能量在空间中分布的均匀程度，能量分布越均匀，熵就越大[11]。在物流传输过程中，城市间的不重叠路径越多，则各路径所担负的传输责任相对越少，城市间传输网络分布越均匀。当网络中某道路断裂时，传输任务能继续完成的概率越大，网络的抗毁性亦更强[12]。因此，本文引入熵的概念，用于度量城市间应急物流网络的抗毁性，同时由于全连通网是最为紧凑的网络结构，因此可以以全连通网为标准，研究一般网络的抗毁性[13]。

在N节点物流网络中，城市vi和城市vj之间的抗毁熵记为：

(1)

式中Kij为城市vi和城市vj之间的不重叠路径数。N-1为N节点全连通网任意节点对之间的不重叠路径数。

SE(vi,vj)在[0,1]之间取值，可用来评价节点间的连通抗毁性。SE(vi,vj)=0意味着网络中只要有1条边断裂，城市vi与城市vj即有可能失去联系。随着SE(vi,vj)取值的增加，两城市节点间的连通抗毁性逐渐增强。当网络为各节点间均有直达边的全连通网时，节点间抗毁性最强，SE(vi,vj)取到最大值1。

接下来我们提出一种当网络中某些道路断裂失效时，各城市在整个应急物流系统中与其他城市保持连通能力的节点稳定性度量指标为：

(2)

这里的节点稳定性不是很多文献中所提到的节点重要性评估指标，而是从考虑城市自身连通安全性角度提出的度量指标。SE(i)在[0,1]之间取值，SE(i)越大，说明节点i越稳定，某些链路断裂后，节点i被孤立的可能性越小。对SE(i)偏小的薄弱节点应增建与其他节点间的链路，以改善其稳定性。

最后，通过计算各节点的稳定熵均值，可以得到整个应急网络系统G的抗毁性指标：

(3)

SE(G)取值越大，说明网络结构越紧凑，当网络局部遭到破坏，全网保持连通的抗毁能力越强。反之SE(G)取值越小，网络的结构越疏松，抗毁性越弱。仅当N节点网络G为全连通网，n个节点的稳定熵SE(i)均取值为1时，网络的整体抗毁性SE(G)=1取最大值。

三、算例分析

(一)算例1

以图1中的6节点8边应急物流网络为例，分别计算各节点的稳定熵系数：

节点v4的稳定性最差，一旦v4与v5间的边断裂，v4即被孤立。

为了验证基于稳定熵的节点抗毁性评估方法的准确性，分别在随机破坏1、2、3条边的情况下，计算各节点被孤立的概率，结果如表1所示，与用本文方法计算得到的结果相一致。

表1　当边断裂时各节点被孤立的概率

为改善城市v4的连通稳定性，对图1中的网络结构进行微调，添加连接城市v3与城市v4的道路v3-v4,同时从成本的角度考虑，删除边v3-v5，保证网络所含边数不变。调整后网络如图2所示。

图2　调整后的6节点8边网络

重新计算各节点的稳定熵系数：

SE(v2)=SE(v3)=SE(v5)=SE(v6)=0.58

SE(v1)=SE(v4)=0.43

再利用公式(3)分别计算调整前后的网络抗毁熵：

SE(G2)≥SE(G1)，从整体抗毁性熵来说,调整后的网络G2(6,8)明显优于调整前，而且所有节点的稳定性均有提高，尤其是节点4的稳定性有了大幅度提升。且在8条道路中即使同时断裂3条边，仅有3.57%的节点被孤立，这个概率在现实中是完全可以接受的。

(二)算例2

假设某区域内含有8个节点，计划在节点间构建12条路径用于物流运输。经过抽象后的两个备选方案的拓扑结构如图3和图4所示。

图3　8节点12边算例网络(G3)

图4　8节点12边算例网络(G4)

在网络G3中，各节点相互对称，

在网络G4中，双数节点i=2,4,6,8时，

SE(G3)≥SE(G4)，网络G3整体抗毁性优于网络G4。同时给出边遭随机破坏时，各网络遭损毁不再连通的比例(见表2)，与基于稳定熵的节点抗毁性评估方法所得结果一致。

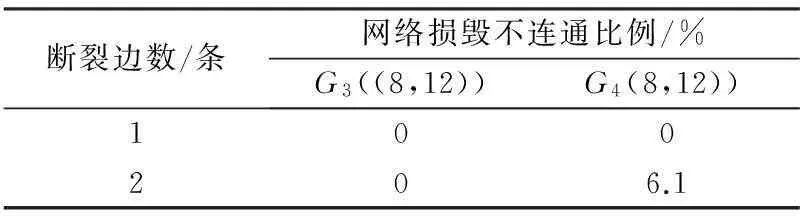
表2　边遭随机破坏后网络的损毁比例

四、结语

本文引入熵的概念，提出了基于熵的应急物流网络节点稳定性度量指标，进而得到网络整体抗毁性。该方法不仅可以对全网整体抗毁性进行度量，还可以对每个节点与外界连通的抗毁性能力进行评估,从而可以找出网络中的薄弱节点，更有针对性地改善网络结构，使网络具有更强的稳定性。

参考文献

[1]陈春霞.基于复杂网络的应急物流网络抗毁性研究[J].计算机应用研究.2012，29(4): 1260-1262.

[2]赵林度.城市重大危险源应急物流网络研究[J].东南大学学报：哲学社会科学版，2007，9(1)：27-29.

[3]周凌云，顾为东，周晶.区域应急物流服务网络动态组建与调度优化决策[J].统计与决策，2013(18):37-39.

[4]陈 坚，晏启鹏，霍娅敏，等.基于可靠性分析的区域灾害应急物流网络设计[J].西 南 交 通 大 学 学 报，2011，46(6)：1025-1031.

[5]孙 君，谭清美，张中华.应急物流网络系统干扰影响及应对能力研究[J].科技管理研究，2014(20)：218-225.

[6]Bengang Gong,Xiang Chen,Chaozhong Hu.Fuzzy entropy clustering approach to evaluate the reliability of emergency logistics system[J].Energy Procedia,2012(16)：278- 283.

[7]陈小可.应急物流网络鲁棒性问题研究[D].北京：北京工商大学，2010.

[8]Xinyong Zhao，Shi An，Haozhe Cong.Traffic incident situation evaluation based on road network reliability of invulnerability[J].Journal of Transportation Systems Engineering and Information Technology，2013，13(10)：79-85.

[9]Xingzhao Peng,Hong Yao,Jun Du,et al.Invulnerability of scale-free network against critical node failures based on a renewed cascading failure model[J].Statistical Mechanics and Its Applications,2015，421(3) ：69-77.

[10]吴六三，谭清美.基于网络熵的应急物流网络稳定性研究[J].当代财经，2012(7)：60-68.

[11]姜璐.熵——描写复杂系统结构的一个物理量[J].系统辩证学学报，1994(4)：50-55.

[12]赵静娴.基于熵的赋权网络抗毁性评估方法[J].计算机应用，2014，34(9)：2627-2629.

[13]赵静娴.基于不重叠路径熵的网络抗毁性评估方法[J].计算机应用研究，2015(3)：825-826，851.

[责任编辑彭国庆]

收稿日期：2015-12-29

基金项目：天津市哲学社会科学规划项目(编号：TJYYWT15-016、TJGL12-101).

作者简介：赵静娴，天津科技大学经济管理学院讲师，博士，主要从事物流管理、数据挖掘和金融工程研究.

中图分类号：TU984.11+6

文献标志码：A

文章编号：1009-3699(2016)04-0439-04