利用高阶累积量的数字调相信号识别

赵知劲，强芳芳，陈　颖

(杭州电子科技大学通信工程学院，浙江 杭州 310018)



利用高阶累积量的数字调相信号识别

赵知劲，强芳芳，陈颖

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

摘要：针对BPSK，QPSK，8PSK，16PSK，OQPSK和π/4-QPSK信号的识别，首先推导16PSK信号的高阶累积量理论值，利用四阶、八阶累积量特征解决四阶、六阶累积量特征参数无法识别16PSK信号的问题，并将6种信号分成4类.针对传统高阶累积量特征参数无法区分QPSK与OQPSK信号及π/4-QPSK与8PSK信号，利用差分累积量特征参数.用3种特征参数识别6种信号，实现了用较少的特征参数识别更多信号的目的.仿真结果表明，在低信噪比条件下能很好地抑制高斯白噪声，在信噪比大于6 dB时，所有信号识别率均达100%.

关键词：调制识别；高阶累积量；差分处理；特征参数

0引言

调制信号识别是军用和民用领域的重要技术，已引起国内外学者的广泛关注[1-2].利用高阶累积量识别调相信号的成果已有许多.文献[3-4]分别用四阶累积量和二阶、八阶累积量区分BPSK，QPSK，8PSK信号.由于OQPSK与QPSK信号累积量相同，π/4-QPSK与8PSK信号累积量相同，文献[5]提出采用相对欧氏距离法和统计相位差法分别识别这两组信号，但在低信噪比情况下识别率不高；文献[6]采用瞬时自相关处理方法识别8PSK，π/4-QPSK，π/4-DQPSK信号，计算方法复杂；文献[7]采用差分累积量方法有效识别了8PSK和π/4-QPSK信号.从目前的公开文献看，几乎没有对16PSK信号识别进行研究.本文研究了BPSK，QPSK，8PSK，16PSK，π/4-QPSK和OQPSK的类内识别，推导了16PSK信号的累积量和OQPSK与QPSK信号差分累积量，利用各类调制信号的八阶累积量和差分累积量，提出3个特征参数，实现了这6种调相信号的识别.

1数字调相信号模型

假设在接收端得到的复基带信号表达式为[4]：

(1)

式中：ak为码元序列，k=1,2,…,N，N表示码元长度，p(t)表示基带码元波形，Ts为码元宽度，A为信号能量，Δθc为相位抖动，n(t)为零均值的复高斯白噪声.

根据数字调相信号性质，对于MPSK信号式(1)中的ak，可以表示为：

ak∈{ej2π(m-1)/M,m=1,2,…M},

(2)

其中，M表示进制数，对应本文所采用的信号，M的取值为2，4，8和16.

OQPSK是QPSK的改进型，相位只能跳变0°，±90°，即若ak∈{ej2π(m-1)/4,m=1,2,3,4}，则ak∈{ej[2π(m-1)/4+Δθ],m=1,2,3,4,Δθ=0,±π/2}.π/4-QPSK信号相邻码元分别属于有π/4相位差的信号集[7]，即若ak∈{ej2π(m-1)/4,m=1,2,3,4}，则ak+1∈{ej[2π(m-1)/4+π/4],m=1,2,3,4}.

本文对每个码元采取1个样本，可得基带采样信号为：

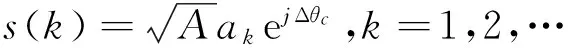
(3)

2特征提取与决策分类

2.1高阶矩与高阶累积量

设有1个均值为0的平稳复随机信号X(t)，定义其P阶混合矩为[8-9]：

Mpq=E[X(t)p-qX*(t)q].

(4)

可得其二阶、四阶、六阶、八阶累积量C20，C21，C40，C42，C60，C63和C80分别为：

C20=Cum(X,X)=M20,

(5)

C21=Cum(X,X*)=M21,

(6)

(7)

C41=Cum(X,X,X,X*)=M41-3M20M21,

(8)

(9)

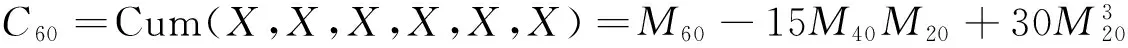
(10)

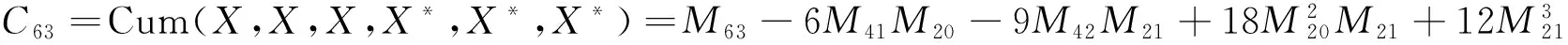
(11)

(12)

2.2MPSK，π/4-QPSK，OQPSK的分类识别

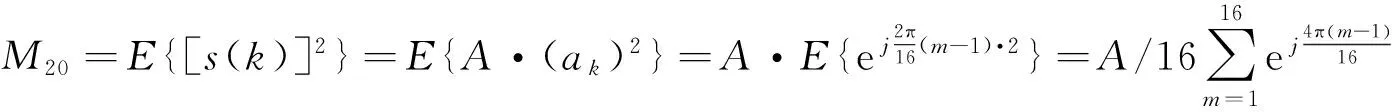
(13)

根据复正弦序列的正交特性可得M20=0.

类似可推得M21=A，M40=M41=M60=M61=M62=M80=0，M42=A2，M63=A3.根据式(5)-(12)，计算得到16PSK信号的各阶累积量理论值.将BPSK，QPSK，8PSK，16PSK，OQPSK，π/4-QPSK信号的累积量理论值一并列表，如表1所示.

表1　各调制信号累积量理论值

(14)

根据式(14)给定3个判决阈值：th1，th2和th3，用特征参数f1和决策分类法可识别4类信号：BPSK，16PSK，{QPSK,OQPSK}和{8PSK,π/4-QPSK}.

2.3QPSK与OQPSK的识别

从表1可以看出，QPSK与OQPSK的累积量完全相同，但QPSK与OQPSK信号的相位跳变规律不同，故可对采样序列式(3)作差分运算，得：

(15)

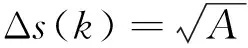
(16)

类似可推得M21=2A，M40=2A2，M41=0，M42=6A2.根据式(5)-(9)，可计算得QPSK差分信号的各阶累积量理论值如表2所示.

表2　QPSK与OQPSK差分信号四阶累积量理论值

对于OQPSK信号，ak+1和ak相关，相邻码元的相位差为Δθ=0,±π/2，概率分别为1/3.此时：

(17)

类似可推得M20=M41=0，M40=-8A2/3，M42=8A2/3.根据式(5)-(9)，可得OQPSK差分信号的各阶累积量理论值如表2所示.

(18)

给定判决阈值th4，利用特征参数f2可识别QPSK和OQPSK信号.

2.4π/4-QPSK与8PSK的识别

π/4-QPSK与8PSK差分信号星座图完全不同.类似求得其差分信号累积量如表3所示.

表3　π/4-QPSK与8PSK差分信号累积量理论值

(19)

给定判决阈值th5，利用特征参数f3可识别π/4-QPSK和8PSK信号.

2.5决策识别流程

分析可得BPSK，QPSK，8PSK，16PSK，π/4-QPSK和OQPSK的识别流程如图1所示.

图1　信号识别流程图

3算法仿真与性能分析

随机产生N个码元，噪声为零均值的高斯白噪声.

取N=3 000，分析每个特征参数的100次仿真平均值随信噪比变化曲线.由于特征参数f1的取值范围比较大，为便于观察，在图2中分(a)，(b)两张图呈现.

图2　不同信噪比下特征参数f1的值

由图2可见，BPSK，QPSK，8PSK与16PSK的特征参数f1的区分度明显，且当信噪比大于6 dB时，分别与理论值基本相同.文献[3]识别BPSK，QPSK和8PSK信号需2个特征参数，且不能识别16PSK信号，而本文只需1个特征参数即可明显区分这4种信号.

QPSK和OQPSK信号的特征参数f2随信噪比的变化曲线如图3所示，π/4-QPSK和8PSK信号的特征参数f3随信噪比的变化曲线如图4所示.

图3　QPSK与OQPSK

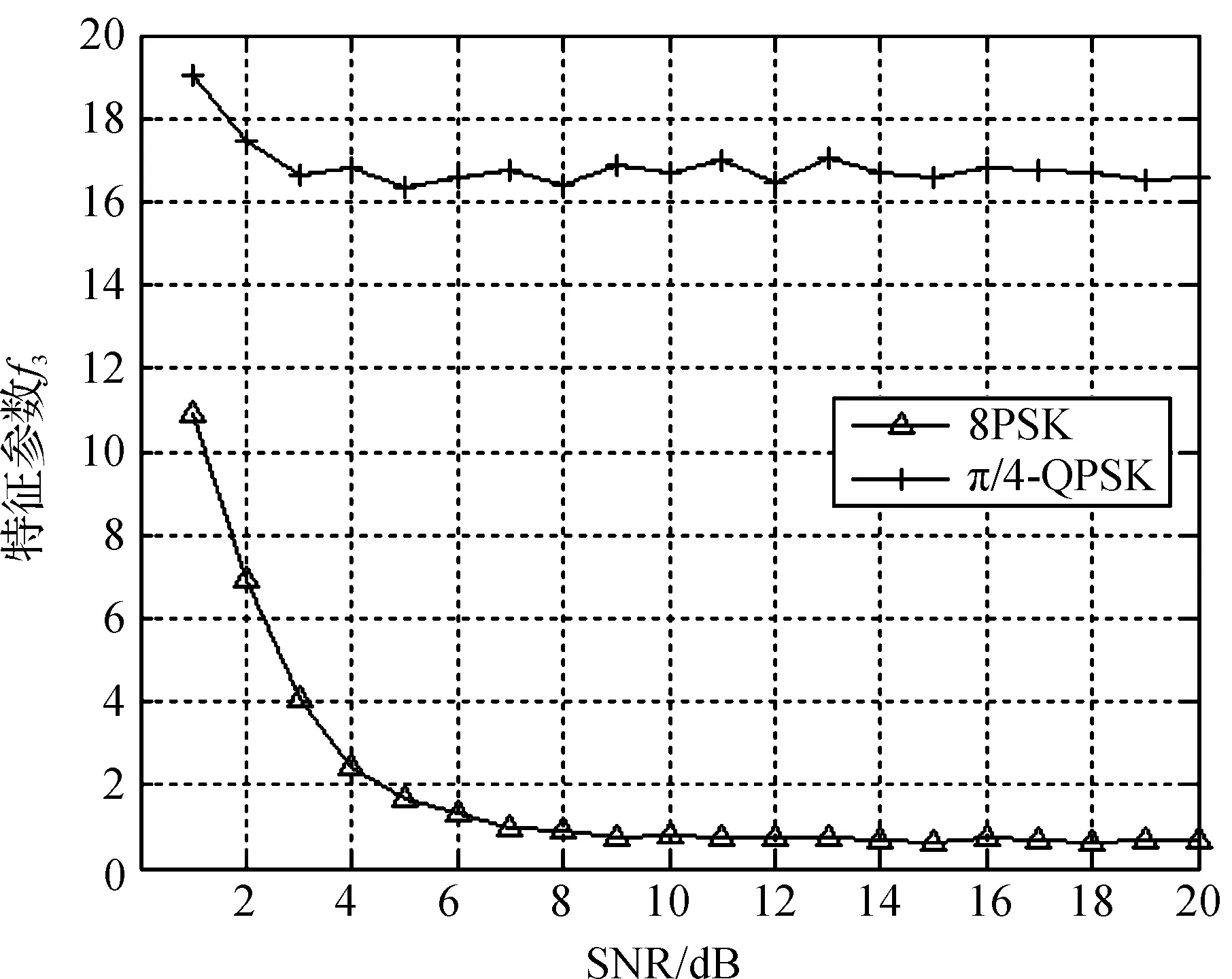
图4　π/4-QPSK与8PSK

由图3和图4可见，信噪比大于7 dB时估计得到的信号特征参数f2，f3与理论值基本相同，且都具有明显的区分度.表明了利用特征参数f2实现QPSK与OQPSK信号识别、利用f3实现π/4-QPSK与8PSK信号识别是可行的.

取N=3 000，理论上各阈值可取为相邻特征参数的中间值，即th1=51，th2=17.5，th3=0.5，th4=2和th5=8.8.由于噪声影响，发现th3和th5的取值对π/4-QPSK信号的识别率存在一定影响，所以微调2个阈值.最终选定为th3=0.4，th5=6.不同信噪比条件下对所有信号分别进行200次仿真，得到每种信号的正确识别率如图5所示.

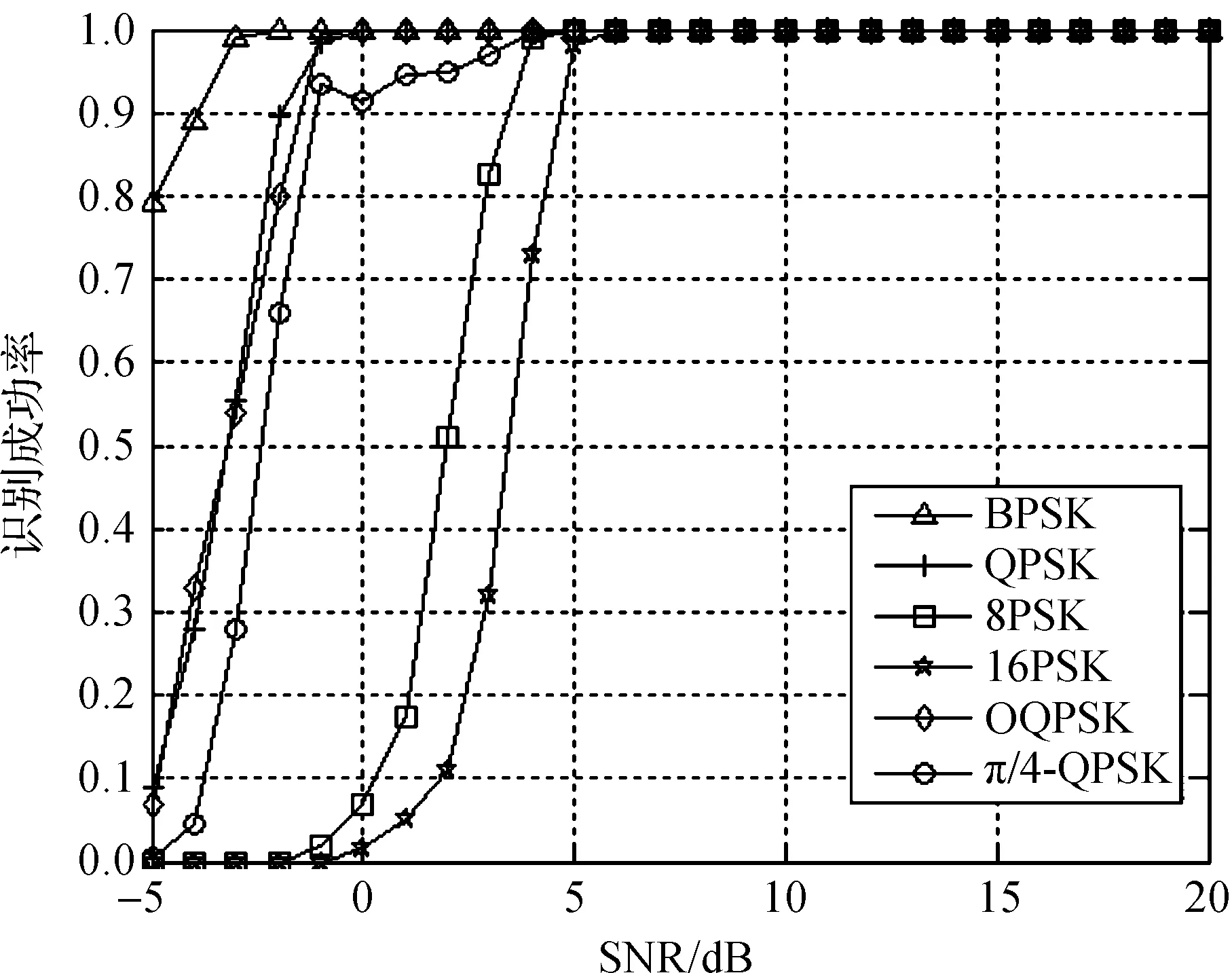
图5　不同信噪比下正确识别率

由图5可见，本文方法正确识别率达到100%时，BPSK，QPSK，OQPSK，8PSK，π/4-QPSK和16PSK分别需信噪比-2dB，0dB，0dB，5dB，5dB和6dB，而文献[4]方法对QPSK和8PSK信号识别率达到92%时需要信噪比为6dB以上；且本文提出的特征参数还能识别16PSK信号.文献[5]方法对QPSK和OQPSK信号的正确识别率达到100%时至少需要信噪比5dB；综合来看，本文只需构造3个特征参数就能在低信噪比条件下正确识别出这6种信号.

4结束语

本文推导了调相信号的累积量和差分信号累积量，用3种特征参数有效实现了6种数字调相信号的识别.本文选取的特征参数少，算法简单；特征参数受噪声的影响小，具有良好的抗相位抖动能力，提高了识别性能；解决了四阶、六阶累积量特征参数不能识别16PSK信号的问题.

参考文献

[1]AZZOUZEE,NANDIAK.Automaticidentificationofdigitalmodulationtypes[J].SignalProcessing, 1995, 47(95):55-69.

[2]SWAMIA,SADLERBM.Hierarchicaldigitalmodulationclassificationusingcumulants[J].Communications,IEEETransactionson, 2000, 48(3):416-429.

[3]杨薇,张晓宁,安洪海.基于高阶累积量的MPSK信号的类内识别[J].通信技术,2010,43(10):43-46.

[4]郭娟娟,尹洪东,姜璐,等.利用高阶累积量实现数字调制信号的识别[J].通信技术,2014,47(11):1255-1260.

[5]NAIKMV,BHATTACHARJEER,MAHANTAA,etal.BlindAdaptiveRecognitionofDifferentQPSKModulatedSignalsforSoftwareDefinedRadioApplications[C]//CommunicationSystemSoftwareandMiddleware, 2006.Comsware2006.FirstInternationalConferenceon.IEEE, 2006:1-6.

[6]薛源,孙小东,杨吉祥,等.利用四阶累积量实现数字调相信号子类识别[J].舰船电子工程,2014,34(11):55-59.

[7]陆凤波,黄知涛,姜文利,等.基于差分高阶累积量的pi/4-QPSK和8PSK调制样式识别算法[J].电子对抗,2007(3):1-5.

[8]张贤达.时间序列分析―高阶统计量方法[M].北京：清华大学出版社,1996：10-17.

[9]SHERMEHAE,GHAZALIANR.Recognitionofcommunicationsignaltypesusinggeneticalgorithmandsupportvectormachinesbasedonthehigherorderstatistics[J].DigitalSignalProcessing, 2010, 20(6):1748-1757.

DOI：10.13954/j.cnki.hdu.2016.03.001

收稿日期：2015-09-07

作者简介：赵知劲(1959-)，女，浙江宁波人，教授，信号处理、认知无线电.

中图分类号：TN911.7

文献标识码：A

文章编号：1001-9146(2016)03-0001-05

Modulation Recognition of MPSK Signals Using Higher Order Cumulants

ZHAO Zhijin, QIANG Fangfang, CHEN Ying

(SchoolofCommunicationEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Abstract：Aiming at the recognition of BPSK、QPSK、8PSK、16PSK、OQPSK and π/4-QPSK signals,higher cumulant theoretical value of 16PSK signal is derived firstly. Four-order and eight-order cumulants feature is used to solve the problem that four-order and six-order cumulants feature can not identify 16PSK signal, and then divide six signals into four classes. Difference cumulant feature parameters are used to recognize QPSK、OQPSK signal and π/4-QPSK、8PSK signal, whom have been not recognized by traditional higher order cumulants. Only three feature parameters are needed to identify all this six signals, and achieve the target of recognizing more signals with less feature parameters at the same time. Simulation results show that this method can suppress Gaussian white noise at low signal noise ratio(SNR) and the recognition rate of all signals reach 100% when SNR>6 dB.

Key words：modulation recognition; higher order cumulants; difference processing; feature parameters