弹丸空气阻力定律超音速段有理式经验公式*
刘 鹏,王雨时,闻 泉,张志彪
(南京理工大学机械工程学院,南京 210094)
弹丸空气阻力定律超音速段有理式经验公式*
刘鹏,王雨时,闻泉,张志彪
(南京理工大学机械工程学院,南京210094)
摘要:为了给低伸弹道方程近似解析解提供基础,应用Matlab软件对描述弹丸空气阻力特性的1943年阻力定律和西亚切阻力定律超音速段进行了有理式函数数值拟合,得到了具有较高精度的经验公式。应用这类经验公式,不但可以用于外弹道数值求解时表值阻力定律的编程处理,而且有助于获取低伸弹道方程的近似解析解。
关键词:弹道学;曲线拟合;经验公式;阻力定律;低伸弹道;数值计算
0引言
在外弹道工程计算时,空气阻力系数是重要参量。尽管现代弹丸外形较1943年阻力定律和西亚切阻力定律的标准弹外形有较大改变,弹丸长细比更大,弹形更为复杂,阻力特性变化规律与这两个阻力定律描述有较大不同,但文献[1]的研究表明,在数值计算和仿真、外弹道观测技术以及风洞试验技术飞速发展的今天,经典的弹丸空气阻力定律以其方便使用的特点和足够的准确度,仍能应用于多数弹药和引信工程研制实践。但1943年阻力定律和西亚切阻力定律却都是表值定律,为便于外弹道学数值计算程序编制,并作进一步的解析分析处理,需将表值定理进行曲线拟合,表达成解析形式。在实用中,引信和弹药总体设计与弹道环境估计都需要低伸弹道经验公式。文献[2]曾以三次抛物线分段拟合的方式给出了1943年阻力定律和高阻炸弹阻力定律的解析表达式。其精度虽然不大于4%,但分段过多(3~4段),应用仍不方便,而用于某些特定弹道(如低伸弹道)的近似解析求解,则已不可能了。文献[3]中所给出的1943年阻力定律的阻力函数经验公式,同样由于分段过多(4段)而不便应用。文献[4]以Logistic曲线拟合方式分别给出了1943年阻力定律亚音速段和超音速段的经验解析表达式,但这类表达式仍不适合低伸弹道的近似解析求解。身管武器系统可大致上分为弹丸亚音速和弹丸超音速两大类。跨音速段弹丸气动力特性难以稳定,故弹丸跨音速段武器系统较少。文中旨在寻找1943年阻力定律和西亚切阻力定律1~4 Ma段阻力系数新的简单直观的解析表达式,拟用于超音速段低伸弹道方程的近似解析求解。
11943年阻力定律超音速段曲线拟合
1943年阻力定律表值在超音速段(1~4 Ma)呈现先上升后下降的规律。若采用传统的多项式拟合,则拟合出的多项式幂次过高且对常系数的有效位数要求较高。而其它常见函数(如傅里叶函数、指数函数)的拟合系数过多,方程过于复杂不利于后续解析求解。利用Matlab软件自带的拟合工具箱可视化的优点[5-6],在对1943年阻力定律进行曲线拟合的过程中可直观的观察曲线符合情况。通过比较分析,Matlab拟合工具箱中的有理式(rational)函数能很好的实现拟合。
有理式函数的一般形式为:
(1)
式中:x为曲线的自变量;y为曲线的因变量;m为分母最高次数;n为分子最高次数;pi、qi为拟合曲线的待定系数。
有理式函数的主要优点是在处理复杂数据时具有很高的灵活性;缺点则是当分母处于0附近时存在不稳定性。
利用有理式函数对1943年阻力定律进行拟合时,幂次过低时拟合效果不好,幂次过高容易出现突变且不利于后续解析求解。经试验比较,最终使用的有理式分式的分子分母皆为二次多相式。如图1所示。
对1943年阻力定律采用的拟合方程为:
(2)
利用最小二乘法对曲线进行拟合,求得待定系数为:
p1=0.218 166 476 686 158;
p2=-0.245 838 817 803 349;
p3=0.073 813 571 190 993;
q1=-1.691 999 884 809 146;
q2=0.831 091 598 545 532。
其最大相对误差为2.553%,方差为8.353 5×10-4。

图1 1943年阻力定律曲线拟合
2待定系数有效数字位数的选取
为进一步探讨待定系数有效数字位数对曲线精度的影响,表1中给出了待定系数取不同的有效数字位数时拟合效果的比较结果,图2中给出了待定系数取不同的有效数字位数时的曲线图。
从表1和图2中可以看出,当待定系数有效数字位数为2位和3位时,其拟合效果有一定的偏差;当待定系数有效数字位数为4位时,其拟合效果与最优解的拟合效果已经很接近,应用中可取4位有效数字。

表1 不同的待定系数有效数字位数拟合效果比较
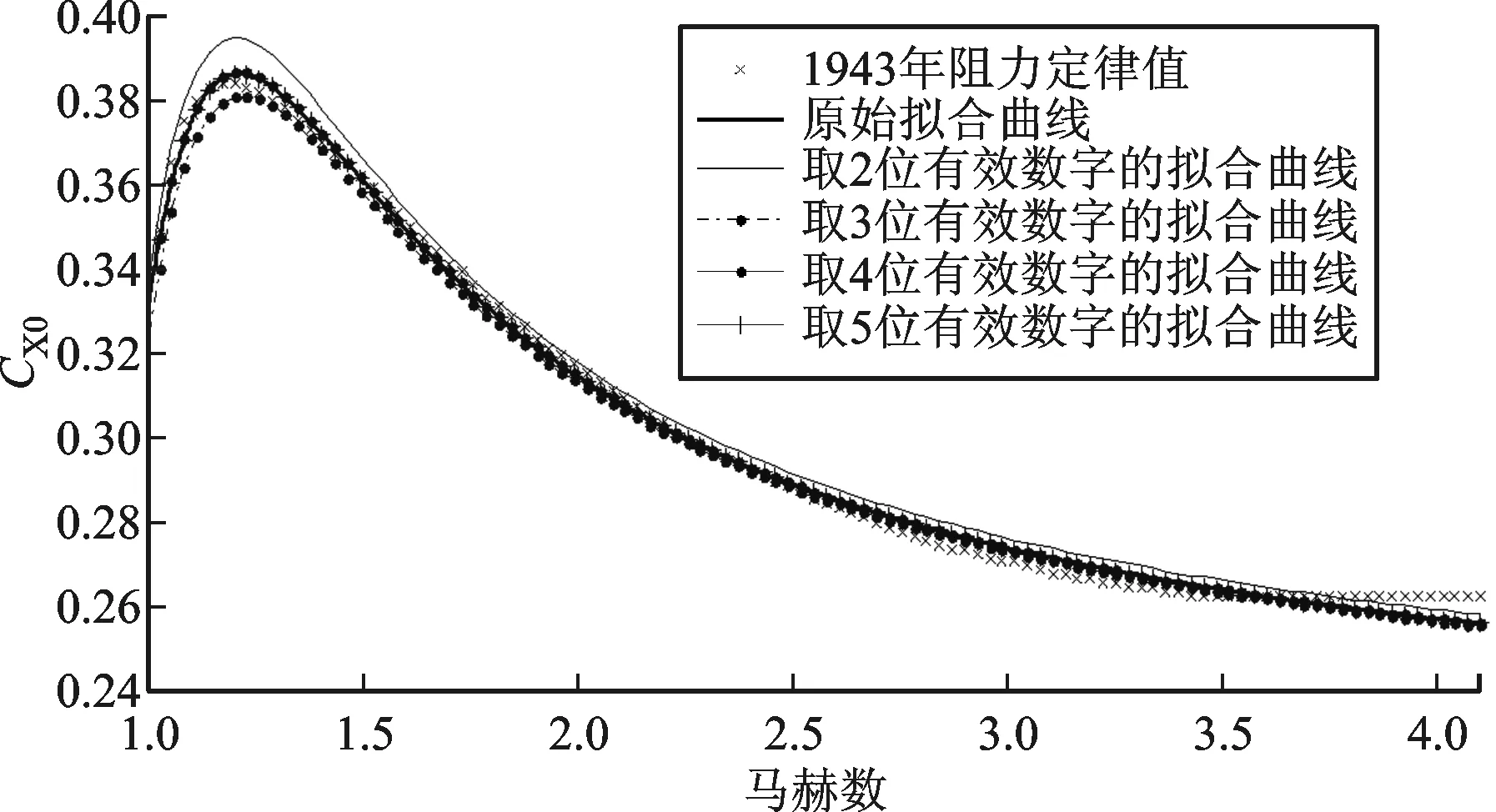
图2 不同的待定系数有效数字位数拟合曲线比较
3待定系数选取方法优化
最优解待定系数位数过多不便于实用,而取一定的有效数字位数又与最优解存在偏差。为解决此问题,可先选取影响因素较小的待定系数(如式中常数项系数p3或q2),对其它待定系数取一定的有效数字位数,确定新的拟合方程,然后再对曲线进行拟合求取待定系数,这样二次求解理论上能提高曲线的拟合效果。
图3给出了取4位有效数字时,不同待定系数选取方法的曲线比较图;表2给出了拟合效果的比较结果。
从图3和表2中看出各种待定系数选取方法的拟合结果基本相同。因此推荐1943年阻力定律在1~4 Ma范围内的经验公式为:

(3)

图3 不同的待定系数选取方法所得拟合曲线比较
4西亚切阻力定律超音速段曲线拟合
西亚切阻力定律已有解析式[3]但应用不便,利用上述方法可对西亚切阻力定律做相同处理,其结果如表3所示。表4给出了待定系数取不同的有效数字位数时拟合效果的比较结果。
从表4中可以看出,利用有理式函数对西亚切阻力定律进行拟合,同样可以取得很好的效果,且估取待定系数的4位有效数字就能满足工程计算需求。

表3 西亚切阻力定律有理式函数拟合方程
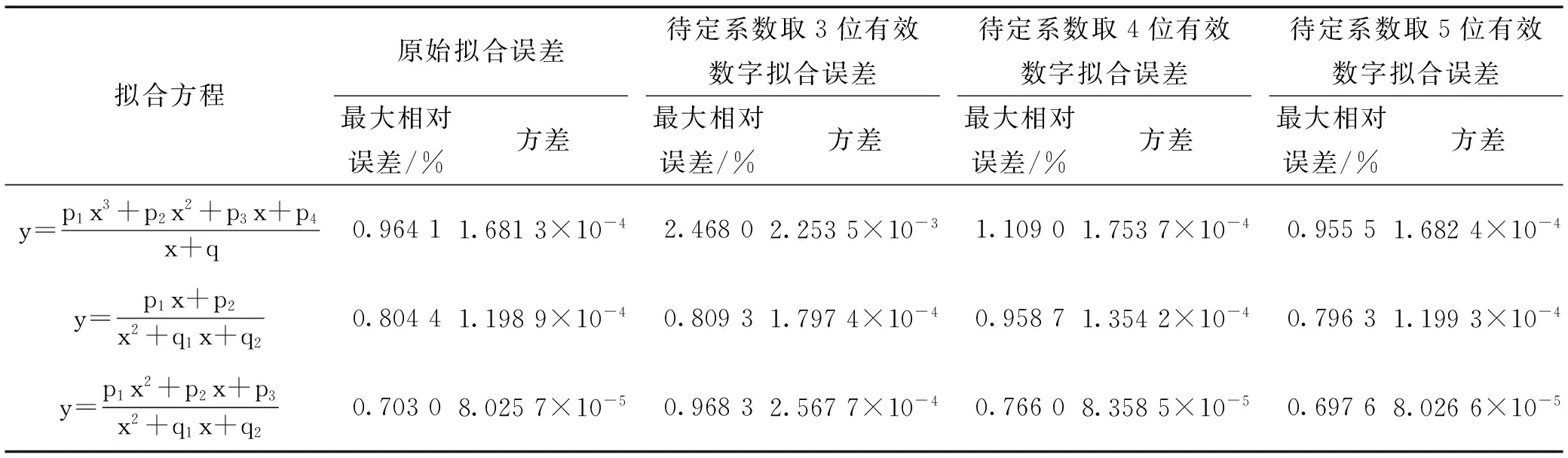
表4 各个拟合方程不同的待定系数有效数字位数拟合效果比较
5拟合曲线跨音速段延伸
为了研究拟合曲线在跨音速段的适应性,表5给出了1943年阻力定律和西亚切阻力定律拟合曲线(待定系数取4位有效数字)在0.85~1 Ma段的误差值。

表5 0.85~1 Ma段各个拟合方程的拟合误差

小。因此推荐西亚切阻力定律在1~4Ma范围内的阻力系数经验公式为:
(4)
6结束语
对于1943年阻力定律和西亚切阻力定律超音速段的曲线拟合,有理式函数都能取得很好的效果。相对于传统的经验公式,该拟合方程对待定系数有效数字位数要求较低,且结构简单,不但可以用于外弹道数值求解时表值阻力定律的编程处理,而且有助于获取超音速段低伸弹道方程的近似解析解。
参考文献:
[1]杨翔, 王雨时, 闻泉. 应用阻力系数拟合曲线解析式数值解算外弹道诸元 [J]. 弹箭与制导学报, 2014, 34(5): 151-155.
[2]王雨时, 焦志刚, 于世杰, 等. 外弹道学阻力定律的三次抛物线分段拟合 [C]∥辽宁省兵工学会第5届学术年会论文集, 1994.
[3]浦发, 芮筱亭. 外弹道学: 修订本 [M]. 北京: 国防工业出版社, 1989: 39-40.
[4]王雨时. 弹丸战斗部及其破片空气阻力系数的Logistic曲线分段拟合 [J]. 弹箭与制导学报, 2006, 26(1): 242-244.
[5]史立新, 聂信天, 季明. 基于Matlab曲线拟合工具箱的列表曲找拟合 [J]. 《新技术新工艺》·软件技术应用, 2007(7): 39-41.
[6]胡庆婉. 使用MATLAB曲线拟合工具箱做曲线拟合 [J]. 电脑知识与技术, 2010, 6(21): 5822-5823.
*收稿日期:2014-10-18
基金项目:江苏省自然科学基金青年基金(BK20140786)资助
作者简介:刘鹏(1991-),男,湖南长沙人,硕士研究生,研究方向:引信及弹药技术。
中图分类号:TJ012.3
文献标志码:A
RationalEmpiricalFormulasforAirResistanceLawofProjectileatSupersonicSection
LIUPeng,WANGYushi,WENQuan,ZHANGZhibiao
(SchoolofMechanicalEngineering,NUST,Nanjing210094,China)
Abstract:In order to lay foundation for approximate analytical expression of low trajectory equation, Matlab software was used to simulate 1943 resistance law and siacci resistance law which describe projectile’s air resistance characteristics by rational curve at supersonic section, the empirical formulas with higher accuracy were obtained. Application of this kind of experience formula can facilitate ballistic numerical solution when processing the table value resistance law programming, and possibly to solve approximate analytical expression of low trajectory equations.
Keywords:ballistics; curve fitting; empirical formula; resistance law; low trajectory; numerical calculation

