基于优化最佳逼近的火箭弹高速侵彻等效缩比方法*
张旭辉,虞跨海,徐红玉,梁 斌,康兴国
(1 河南科技大学工程力学系,河南洛阳 471023;2 西安机电信息研究所,西安 710065)
基于优化最佳逼近的火箭弹高速侵彻等效缩比方法*
张旭辉1,虞跨海1,徐红玉1,梁斌1,康兴国2
(1河南科技大学工程力学系,河南洛阳471023;2西安机电信息研究所,西安710065)
摘要:文中基于优化理论开展了火箭弹高速侵彻等效缩比方法研究。通过量纲分析、优化拉丁超立方方法确定弹长、弹径、弹体初速度及靶标厚度为设计变量的样本空间,高精度数值计算获取设计变量关于弹体过载和持续时间的目标响应,建立快速分析模型,以响应最佳逼近为优化目标,以最小缩比为约束,模拟退火算法实现等效缩比优化模型的求解。优化结果代入侵彻模型进行参数反演,结果表明,缩比模型与原模型的过载特性具有较高的一致性。
关键词:侵彻;优化设计;等效缩比;Kriging模型
0引言
高速火箭弹主要用于精确打击重要军事目标,研究人员不断加大弹体尺寸,通过提升动能提高其破坏能力。传统试验技术、发射条件难以满足大尺寸武器的设计要求,且大尺寸侵彻试验不仅难度大、成本昂贵,且设计周期长。
缩比技术是解决这类武器设计试验问题的有效手段[1],开展缩比试验成本低、规模小,已成为研究火箭弹的重要途径之一。近年来逐渐开展了高速侵彻等效缩比的研究[2-4],研究中主要以钢筋混凝土靶为研究对象开展,关于弹型等效缩比优化及过载特性方面的研究较少,主要采用量纲分析方法开展试验,但这种方法往往要求缩量统一且只能适用于静态或低速冲击问题,并不能满足高速侵彻问题的工程应用需求。
文中基于设计空间采样、代理模型建模、目标逼近优化等方法,探索这种高维、非线性、动力学响应条件下的等效试验方法,为高价值武器的有效试验技术难题提供解决方案。
1几何模型与量纲分析
高速侵彻涉及弹体、靶标的相关参数,其动力学性能指标函数可定义为:
(1)
式中:下标m代表弹体,下标t代表靶标;ρ为密度;E为弹性模量;μ为泊松比;Y为材料强度;H为靶标厚度;R为弹体半径;L为弹长;V为弹体着靶速度;Nrc是弹头形状参数。以ρt、Yt、Lm三个具有独立量纲的基本量表示其它各量,由量纲分析π定理,过载峰值及持续时间可表示为:
(2)
弹体和靶体材料、弹头形式不变条件下,上式可简化为:
(3)
表明动力学性能指标无量纲过载峰值及持续时间仅与无量纲靶标厚度、弹体半径、初始速度和弹体长度相关。图1所示为火箭弹高速侵彻二维截面示意图。
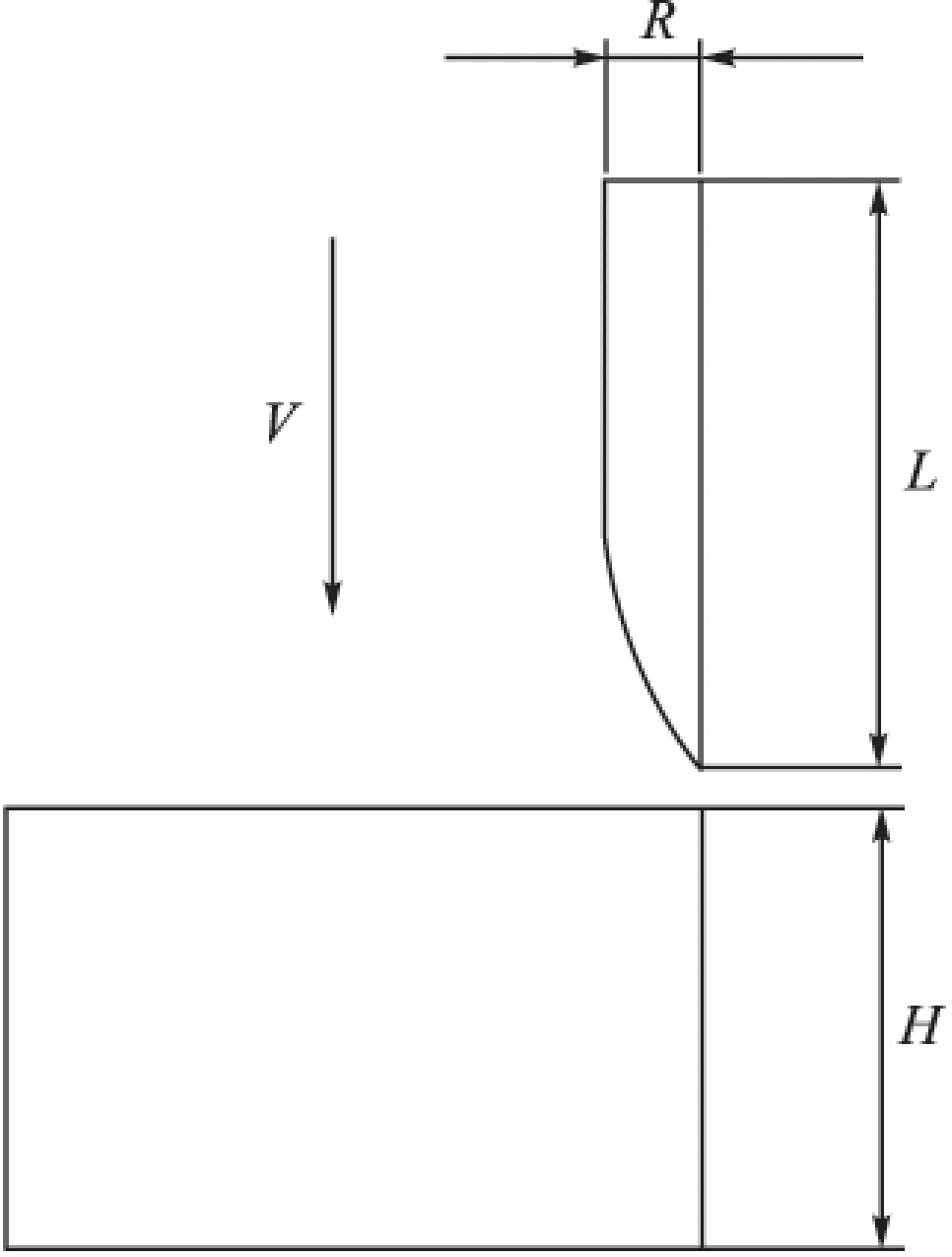
图1 高速侵彻二维截面示意图
2代理模型建模
基于设计变量初值,定义各设计变量取值范围如表1所示,采用拉丁超立方抽样方法设计空间生成初始样本点128个。网格划分为六面体单元,并对侵彻中心域网格进行加密,避免由于网格大变形产生的计算不稳定现象,如图2所示为侵彻几何模型及其网格划分。

表1 设计变量及其取值范围
弹体采用Johnson-Cook材料模型,混凝土采用经典HJC本构模型,模型材料参数如表2所示[5-6]。基于数值分析软件二次开发技术,实现几何模型、数值分析模型建模和计算,并自动保存各样本点弹体最大过载及持续时间。
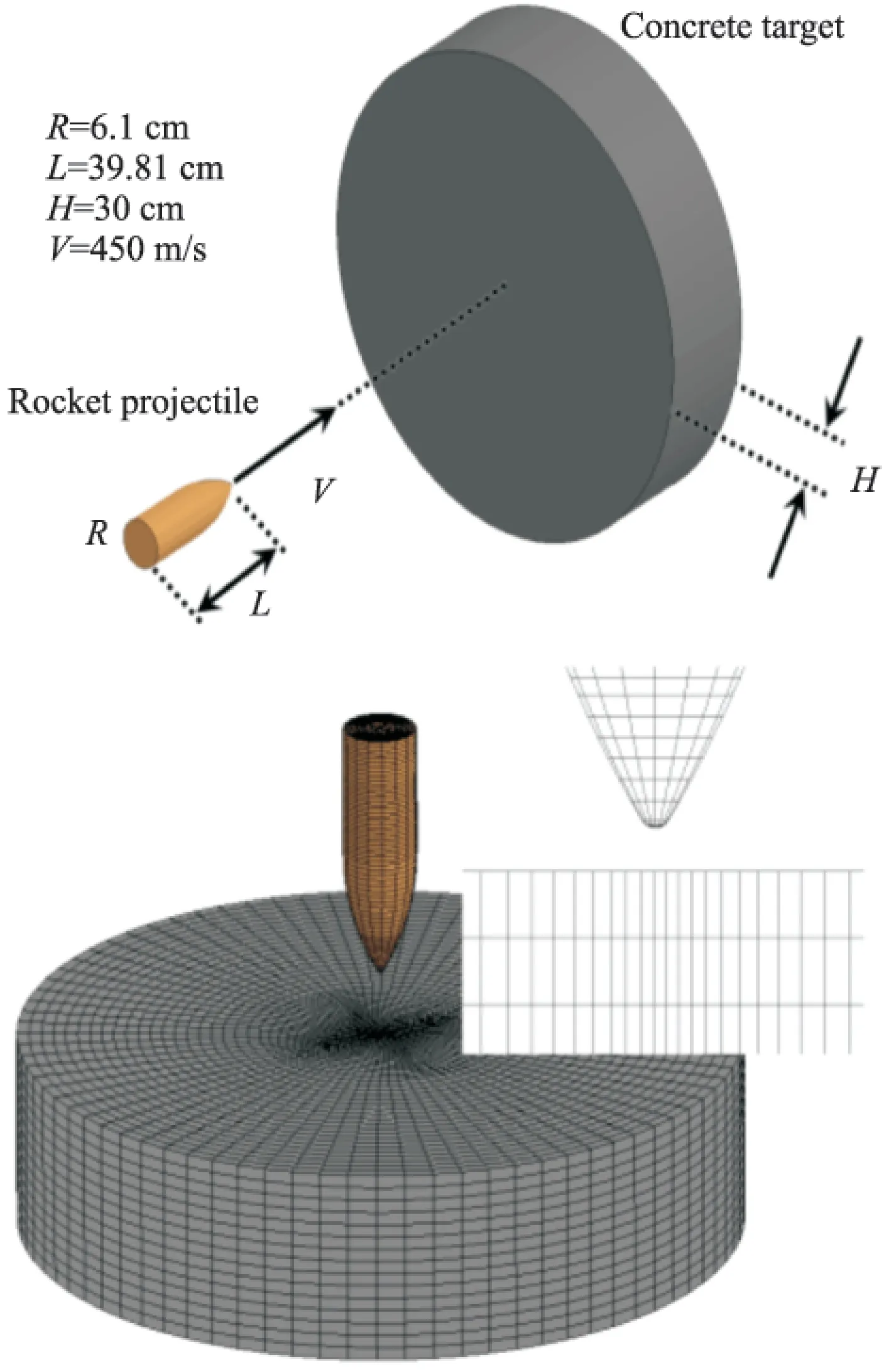
图2 侵彻模型及网格划分
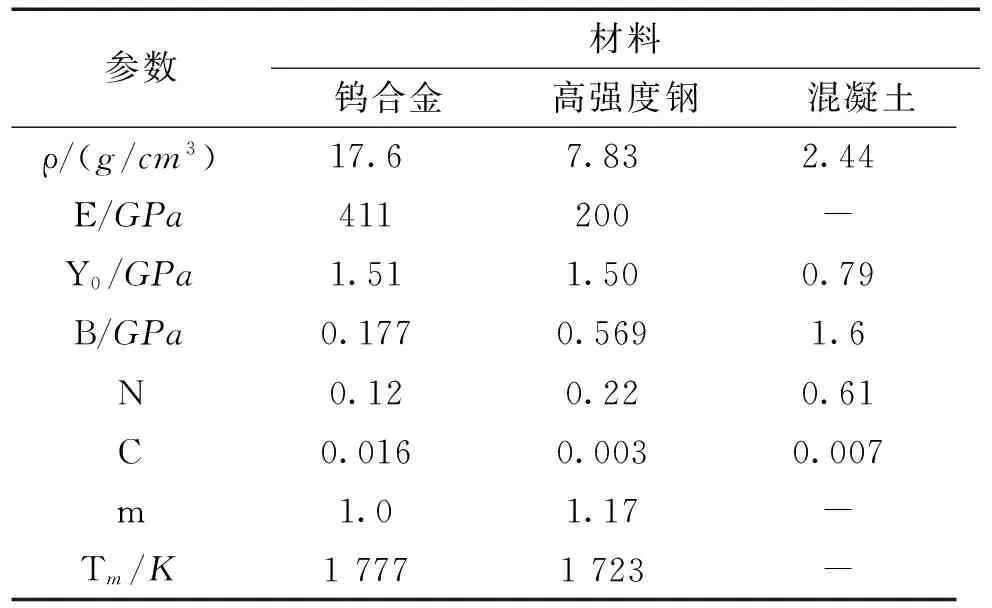
参数材料钨合金高强度钢混凝土ρ/(g/cm3)17.67.832.44E/GPa411200-Y0/GPa1.511.500.79B/GPa0.1770.5691.6N0.120.220.61C0.0160.0030.007m1.01.17-Tm/K17771723-
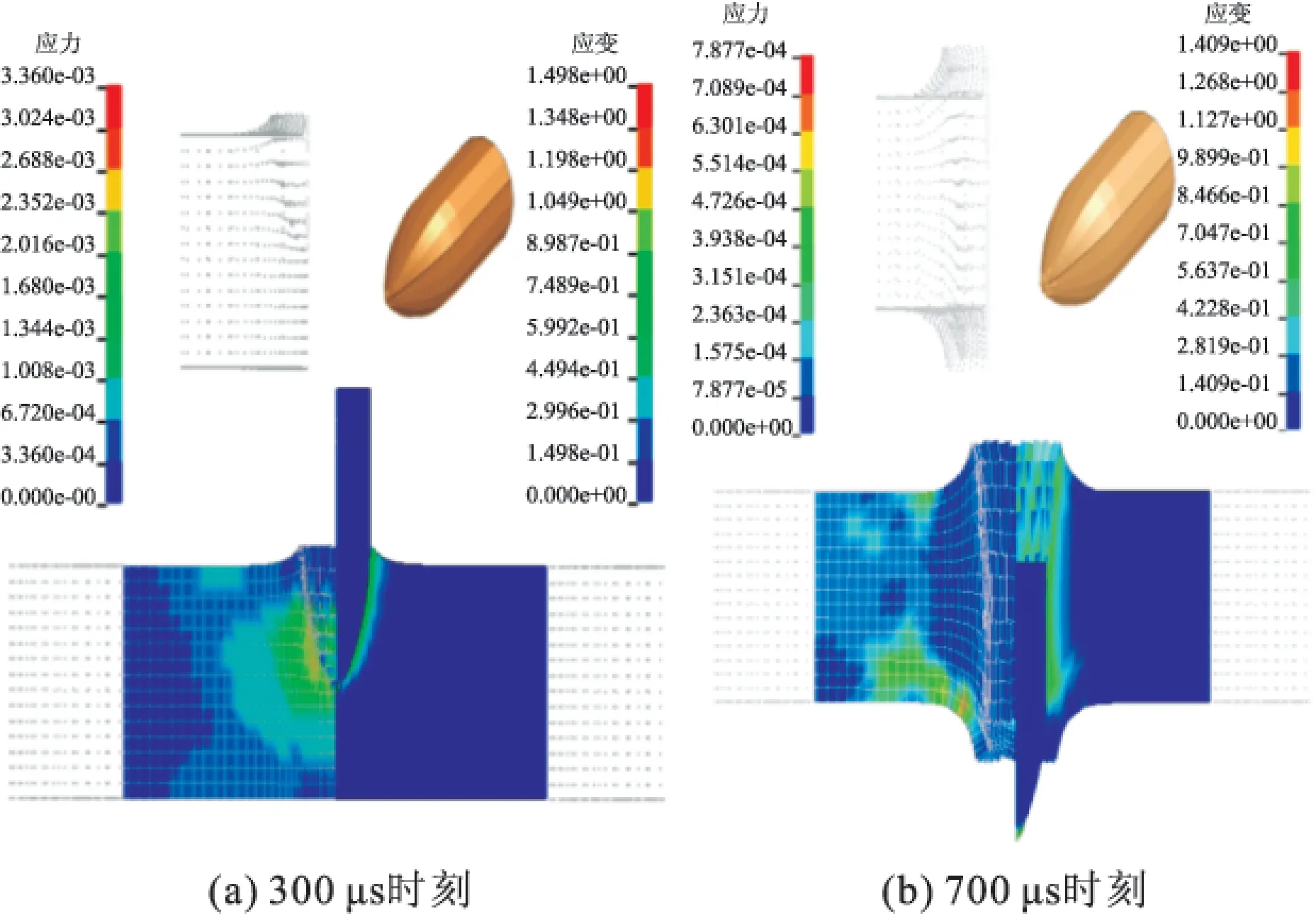
图3 不同侵彻时刻弹靶应力-应变
图3所示为不同侵彻时刻弹靶应力-应变。侵彻初始阶段,靶标形成漏斗状开坑,进入稳定侵彻阶段,靶标成柱形孔道,侵彻过程靶标正背面均出现碎块飞溅现象,形成漏斗状坑型,中间为柱形孔道的侵彻特征,弹坑约1.8倍弹径。
Kriging模型[8]拟合最大过载和持续时间对设计变量的响应函数,基于函数扩展提高代理模型精度,构造设计空间响应的近似模型。图4所示为拟合得到的弹长、弹径与最大过载的空间三维曲面。
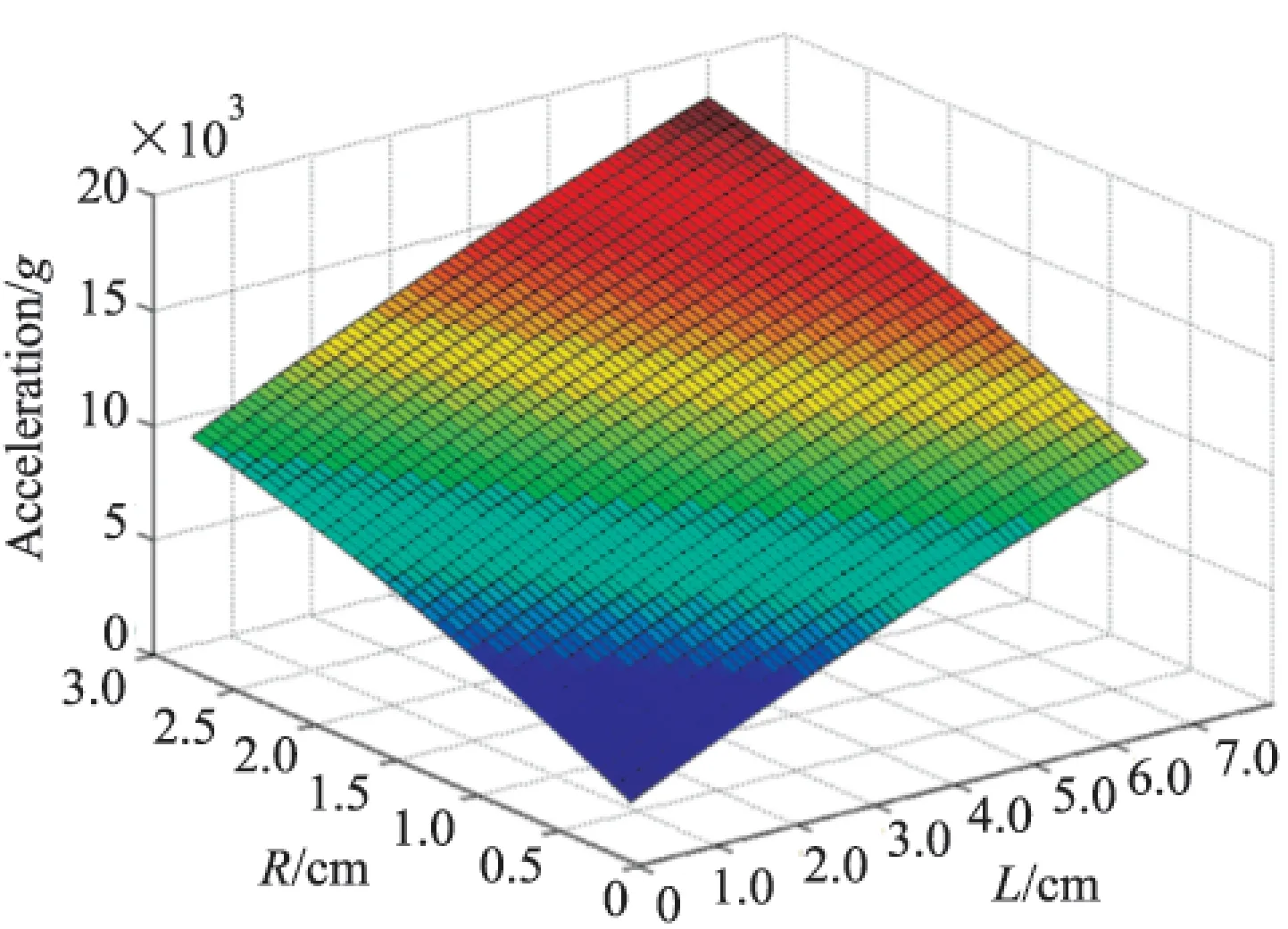
图4 弹长、弹径与最大过载响应曲面
3优化目标及优化策略
定义侵彻弹体最大过载初值amax0和持续时间tmax0,以缩比几何尺寸弹体侵彻最大过载和持续时间与初值最佳逼近为目标函数,建立优化模型。
Minimize:F(X)=(|f1(x)-amax0|,|f2(x)-tmax0|)
其中:xk为设计变量取值,取值范围同表1;f1(x)为最大侵彻过载;f2(x)为侵彻持续时间。采用加权法构造目标函数,为了消除目标变量之间的数值差异,采用无量纲化处理,加权法构造目标函数为:
其中λ1、λ2分别为加权系数,并且有λ1+λ2=1,文中取λ1=λ2=0.5。
图5所示为高速侵彻等效缩比优化流程,以弹长、靶厚、侵彻初速度为优化变量开展优化计算,采用模拟退火算法进行寻优,收敛标准为目标函数或设计变量前后迭代相差小于10-3。

图5 高速侵彻等效缩比优化流程
4优化计算与结果
依据优化流程获取额定弹径下弹体侵彻最大过载和持续时间的最优解,不依赖全尺寸弹试验条件下得到火箭弹侵彻特性参数。表3为高速火箭弹等效缩比各变量优化结果,结果参数代入原侵彻模型进行参数反演,其误差低于10%。
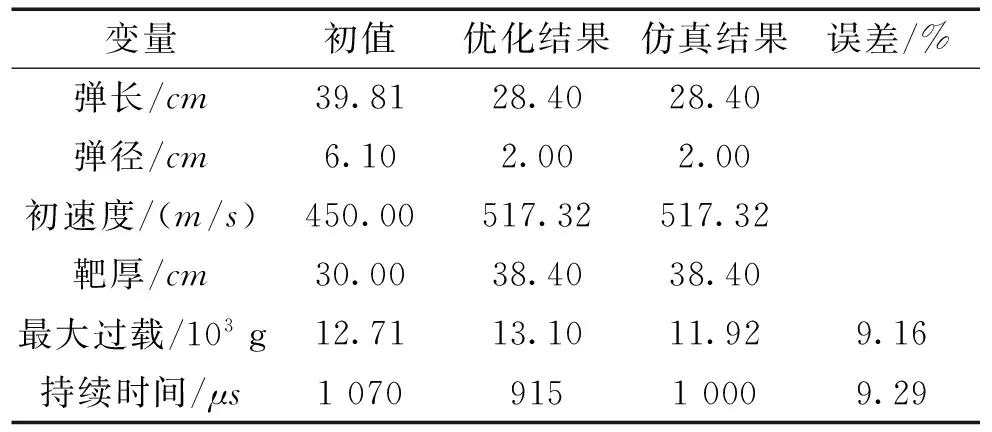
表3 优化设计变量与优化目标
图6所示为初值与优化后参数弹体模型过载曲线,过载峰值和持续时间两项指标表明,缩比后弹体与原尺寸弹侵彻过程动力学响应基本一致,表明文中建立的高速火箭弹侵彻等效缩比模型具有较高的精度,兼顾效率和精度在较低成本条件下实现了侵彻弹的等效缩比,为火箭弹的研制提供理论指导。
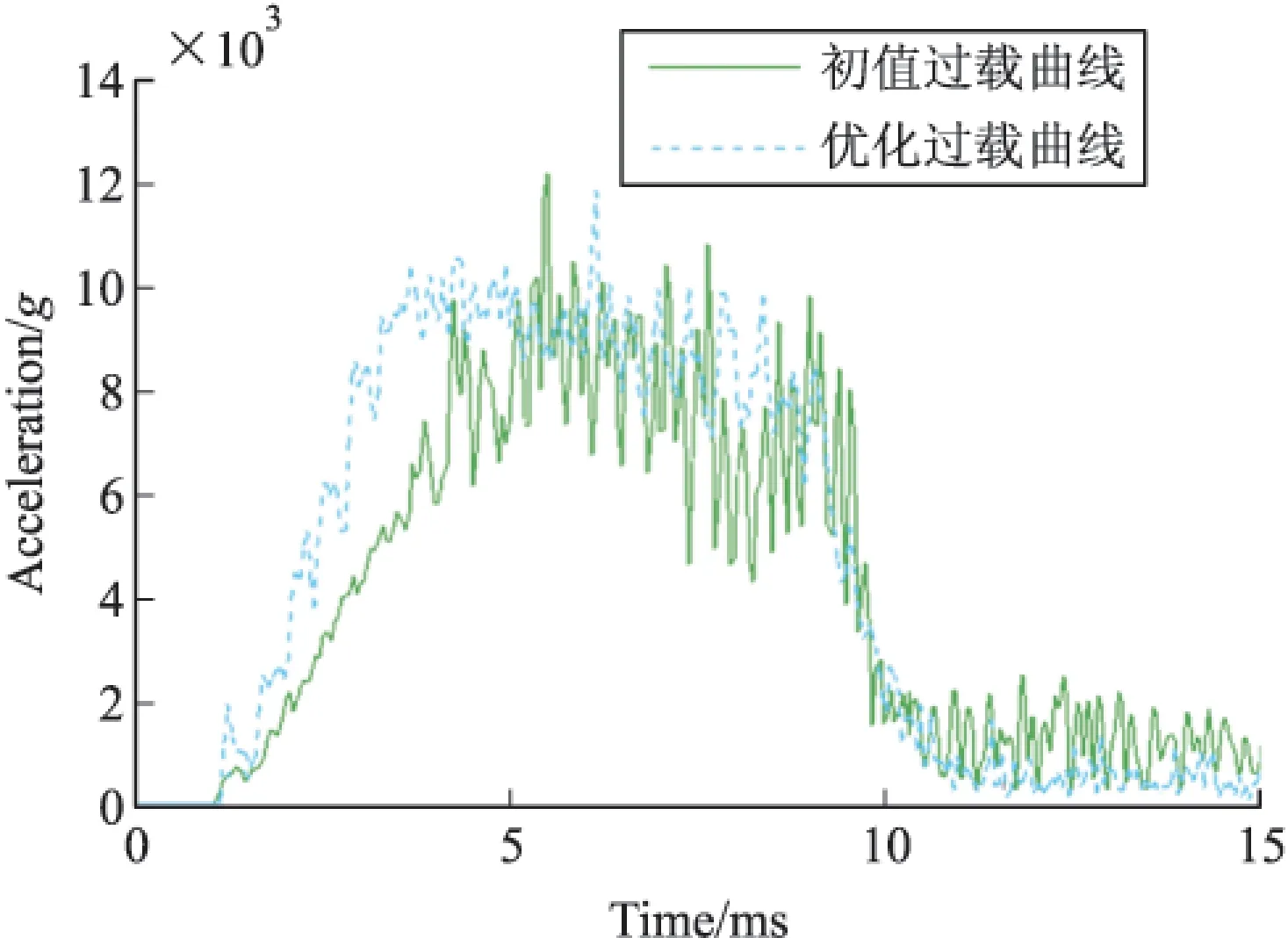
图6 初值与优化后过载曲线
5结论
文中提出了基于数值优化最佳逼近方法获得弹体侵彻缩比尺寸设计的新思路,通过实例的数值建模与仿真计算,得到以下结论:
1)直接基于量纲分析方法的等效缩比模型并不能直接应用于高速火箭弹试验设计;
2)提出的基于设计空间采样、数值仿真计算、代理模型建模和目标函数最佳优化逼近方法的等效缩比试验建模方法可行有效;
3)等效试验几何尺寸可采用非统一缩量比例,以满足试验过程中各项测试的需求,如为便于安装引信结构而保持弹径不变。
参考文献:
[1]程栋, 何国强, 沈百梁, 等. 某型发射动力系统缩比试验方法研究 [J]. 弹箭与制导学报, 2011, 31(2): 60-62.
[2]陈小伟, 张方举, 杨世全, 等. 动能深侵彻弹的力学设计(Ⅲ): 缩比实验分析 [J]. 爆炸与冲击, 2006, 26(2): 105-114.
[3]武海军, 黄风雷, 陈利, 等. 动能弹侵彻钢筋混凝土相似性分析 [J]. 兵工学报, 2007, 28(3): 276-280.
[4]杨超, 赵宝荣, 付克勤, 等. 缩比件弹体侵彻混凝土过程相似律研究 [J]. 兵器材料科学与工程, 2003, 26(5): 3-7.
[5]JOHNSONGR,COOKWH.Aconstitutivemodelanddataformetalssubjectedtolargestrains,highstrainratesandhightemperatures[C]∥ProceedingsoftheSeventhInternationalSymposiumonBallisticstheHague, 1983.
[6]LIUY,MAA,HUANGFL.Numericalsimulationsofoblique-anglepenetrationbydeformableprojectileintoconcretetargets[J].InternationalJournalofImpactEngineering, 2009, 36(3): 438-446.
[7]李靖, 廖瑛, 杨雅君. 基于Kriging模型的QPSO算法在固体运载火箭弹道优化中的应用 [J]. 弹箭与制导学报, 2014, 34(3): 141-145.
[8]YINH.Krigingmodelapproachtomodelingstudyonrelationshipbetweenmolecularquantitativestructuresandchemicalproperties[D].HongKong:HongKongBaptistUniversity, 2005.
*收稿日期:2015-04-01
基金项目:国家自然科学基金(51105132);总装预研基金(9140A0506312BQ4201);河南科技大学研究生创新基金(CXJJ-ZR11)资助
作者简介:张旭辉(1990-),男,陕西渭南人,硕士研究生,研究方向:计算力学及其工程应用。
中图分类号:TJ760;TJ714
文献标志码:A
EquivalentScalingMethodofHigh-speedRocketProjectilePenetrationBasedonOptimizationofOptimalApproximation
ZHANGXuhui1,YUKuahai1,XUHongyu1,LIANGBin1,KANGXingguo2
(1DepartmentofEngineeringMechanics,HenanUniversityofSinceandTechnology,HenanLuoyang471023,China;2Xi’anInstituteofElectromechanicalInformationTechnology,Xi’an710065,China)
Abstract:Based on optimization theory, equivalent scaling method of high-speed penetration projectile was carried out in this paper. Four designed variables were length, radius, initial velocity of projectile and thickness of target, which were determined according to dimensional analysis and Latin Hypercube sampling optimization methods. The designed variables on acceleration and duration of projectile response were obtained through high-precision numerical simulation, the designed variables and objective response were achieved and a rapid analysis model was established, the optimization was to find out approximation to the best response, and the minimum reduction ratio was regarded as constraints, and equivalent scaled optimization was solved by simulated annealing algorithm. Parameter inversion was carried out through the penetration model with optimization results, and the results showed that there was high consistency between the acceleration characteristics of the scaling model and that of the original model.
Keywords:penetration; optimization design; equivalent scaling; Kriging model

