时间约束的异构分布式系统工作流能耗优化算法

蒋军强　林亚平　谢国琪　张世文

1(湖南大学信息科学与工程学院　长沙　410082)2　　　(可信系统与网络湖南省重点实验室(湖南大学)　长沙　410082)



时间约束的异构分布式系统工作流能耗优化算法

蒋军强1,2林亚平1,2谢国琪1张世文1,2

1(湖南大学信息科学与工程学院长沙410082)2(可信系统与网络湖南省重点实验室(湖南大学)长沙410082)

(jjq@hnu.edu.cn)

摘要针对现有异构分布式可变电压频率(dynamic voltagefrequency scaling, DVFS)计算系统下具有时间约束的工作流能耗优化算法易陷入局部最优的问题，提出了一种新的全局能耗优化算法：反向蛙跳全局能耗感知算法,该算法利用工作流下界完成时间和约束时间之间存在的盈余，逐步从约束时间开始，以不同的跃度值向下界完成时间反向蛙跳，在此过程中基于局部最优解的判断不断调整跃度值直至蛙跳终点，同时保留该过程中工作流满足时间约束且任务运行能耗最小的调度序列.在此基础上利用处理器松弛时间回收技术，在保持任务间依赖关系和满足工作流时间约束的前提下，调整处理器运行电压频率至更低的合适级别上，从而进一步降低工作流运行能耗.实验表明：该算法能显著降低工作流整体能耗，节能优势明显.

关键词异构分布式系统；能耗优化；时间约束；工作流；松弛时间回收

自世界上第1台电子计算机“ENIAC”诞生至今，计算机已进化成各种形状、尺寸和规模的机器，成为人们日常生活中随处可见的物品(如手机).与此相对应，计算系统也由最初的单一同构式发展到今天的异构分布式[1]，其体系结构表现越来越灵活.异构分布式计算系统是将物理上分散的多台计算机通过通信网络相互联结组成逻辑上集中的系统对外提供计算服务，系统中各计算机硬件、软件以及组成该系统的网络间的通信协议不尽相同[2].近年来，新的异构分布式计算模式和技术不断被提出，如对等网络(peer-to-peer computing)[3]、网格计算(grid computing)[4]和云计算(cloud computing)等[5].尤其是后者的提出，使得异构分布式计算系统的发展呈现风起云涌之势.时至今日，云计算已经成为一种成熟的技术被各大IT公司和科研机构所广泛采用，应用在大数据处理、科学研究分析、复杂工作流处理等多个场景.同时，各大IT公司纷纷推出自己的云计算产品对公众提供服务，如Amazon的EC2[6]、Google的App Engine[7].这些产品使用Hadoop[8],Spark[9]等软件，组织起数量众多、位置分散、性能各异的物理计算节点来构成庞大的计算资源平台，因此，云计算是一种典型的异构分布式计算系统.此外，伴随信息爆炸式增长而产生的大数据[10]，其存储中心通常意义上也属于异构分布式计算系统[11-12].

庞大的系统必然对应着巨大的能量需求.有研究表明：一个拥有5万个计算节点的数据中心一年所耗费的电量约为1×108kW·h，这相当于一个10万人口规模城市一年的耗电量[13].谷歌数据中心一年的耗电量高达1.12×109kW·h，随之而来是其每年高达6 700万美元的电费支出[12].此外，大型系统必不可少的辅助设施(如风冷系统)使得这些系统耗能越发巨大.高耗能也意味着大量的二氧化碳排放，有文献指出，在美国每消耗1度电平均产生500 g的二氧化碳排放[14]，进一步加剧了地球的温室效应以及对环境的破坏，在倡导“绿色计算”的今天，这无疑受人诟病.另外，高耗能通常与高电压对应，高电压更容易使电子元器件产生高温，如果计算节点长期处于高温状态下，无形中增加了计算节点出现潜在故障的几率[15].因此，考虑异构分布式计算系统下的能耗问题具有重要的应用意义.

1相关工作

科学研究、电子商务等领域的许多应用均可看做是工作流——一种面向过程建模和管理的核心技术，常可用有向无环图(directed acyclic graph, DAG)表示[20-21].用户将工作流提交到计算系统后，一般会有附加的服务质量(quality of service, QoS)要求，如费用、执行时间、可靠性等.用户期望工作流在执行时满足QoS要求，因此，基于QoS的工作流调度问题就是在所有满足QoS的调度中选择最合适的调度执行.

基于QoS的调度问题通常情况下是一个NP-难问题，已有许多文献提出相应的优化算法[22-29].时间约束作为常见的QoS要求，出现在诸多应用场景中，如实时天气预报系统、在线视频点播系统等.同样地，能耗优化近年来越来越受到工业界和学术界的关注，尤其是针对耗能巨大的大型异构计算系统譬如云计算平台和数据中心.其中既有通过合理措施降低自身运行能耗[11,14,24]，也有利用可再生能源实现碳减排[12]，对绿色计算的发展起到了非常积极的促进作用.进一步地，针对具有先序约束的DAG工作流调度中的时间和能耗2个颇受用户关注的问题，在异构分布式可变电压频率计算系统下，Lee等人[25]提出ECS算法，该算法利用目标函数来权衡能耗优化与执行时间之间的关系，从中选取函数值为最大正数值的处理器与电压频率组来执行任务，本文同时也显要地指出该算法不适合具有时间约束的实时系统.Li[26]将这个多目标优化问题细分为3个问题：能耗约束下的工作流最小完成时间问题、时间约束下的能耗最小问题以及二者的综合，并提出了相应的算法，但算法针对的是具有先序约束的串行工作流.Su等人[27-28]提出可利用部分最优化松弛技术将处理器的松弛时间回收，进而降低任务的运行电压达到节能的目的，但根据文中的描述该算法更适合线性可变电压频率处理器场景.Tang等人[29]则提出在原始调度基础上逐步关闭利用率不高的计算节点，在剩余计算节点上重新执行调度直至调度完成时间大于约束时间，再在此基础上使用改进的Su的方法进一步降低系统整体运行能耗，但在实际环境中直接关闭计算节点显得不切实际.

本文以异构分布式可变电压计算系统下具有时间约束的DAG工作流调度能耗优化问题作为研究对象.基于约束时间与下界完成时间之间的盈余，引入最小跃度值与最大跃度值概念，逐步从约束时间开始，以不同的跃度值向下界完成时间反向蛙跳，每次跳跃均可以形成一大一小2个盈余时间值，分别将此二值附加到各个任务，得到各个任务新的最早完成时间，在此新的时间内各个任务按照优先级对全局所有处理器和电压频率组进行遍历，选取使任务运行能耗最小且对应最早完成时间不大于新的最早完成时间的处理器和电压频率组，将其指派给该任务运行，同时注意保持任务之间的依赖关系.2个不同的盈余时间产生2个满足时间约束的有效调度，基于2个有效调度运行能耗大小的比较结果，重新设定下一轮反向蛙跳的起点与跃度值，同时保留其中运行能耗最小的调度为当前全局最优调度，如此循环反向跳跃直至蛙跳终点.在全局最优调度基础上利用处理器松弛时间回收技术，在保持任务间依赖关系和满足工作流时间约束的前提下，调整处理器的运行电压频率至更低的合适级别上，从而进一步降低DAG工作流整体能耗，最后实验结果表明算法节能优势明显.

2模型及问题定义

2.1系统模型

系统包含k个异构的处理器及计算节点，它们互联组成计算节点集P，P={p1,p2,…,pk}，每个计算节点均部署成可变电压频率模式，即pk∈P可运行在不同的供电电压与时钟频率上.设电压集为V，频率集为F，当处理器运行在电压vl∈V时它对应的时钟频率为fl∈F.当处理器空闲时，它运行在最低电压vmin上以节能，约定最低电压不能为0，即vmin>0.鉴于频率切换时间很小(10～150 μs)，一般不考虑电压切换开销[15,25,29].同时假设各计算节点以同样的速率交换数据，即不存在通信竞争.计算节点执行任务的同时可以同步收发数据[20,25].

2.2应用模型

并行工作流一般可用有向无环图DAG来表示[20-21].一个DAG由节点集N和边集E构成，G=(N,E,W,C)，其中，N由n个节点组成，每个节点表示工作流中的单个任务；E由e条有向边组成，它表示任务之间的依赖关系，边上的权值表示任务之间的通信开销.边(i,j)∈E表示任务nj在收到任务ni的处理结果之前不能启动，ni称为nj的直接前驱任务，nj称为ni的直接后继任务；没有前驱任务的节点称为入口任务nentry，没有后继任务的节点称为出口任务nexit；pred(ni)表示任务ni的直接前驱任务集，succ(ni)表示任务ni的直接后继任务集.

W是一个|N|×|P|(本文用|X|表示集合X的大小)的矩阵，wi,k表示任务ni在处理器pk上，以最高电压频率运行时的计算开销；表示任务ni的平均计算开销，它等于任务ni在所有处理器上的计算开销之和除以处理器个数.C是一个|N|×|N| 的矩阵，ci,j表示ni到nj的通信开销，如果ni与nj运行在同一计算节点上，则它们之间的通信开销为0.

HEFT[20]算法作为著名的单工作流静态调度算法，以其合理的时间复杂度和高效的执行效率，不但被许多研究者引用获得学术界广泛关注，同时也在网格计算框架ASKALON[30]中予以实现，其有效性与实用性得以证明.本文也利用它来处理工作流任务的具体调度问题.与文献[25,27-29]类似，本文的调度模型为离线模型.

参照文献[20]，给出任务ni在处理器pk上的最早启动时间(earliest start time, EST)EST(ni,pk)、最早完成时间(earliest finish time, EFT)EFT(ni,pk)和实际执行时间ti分别为

EST(ni,pk)=

(1)

EFT(ni,pk)=EST(ni,pk)+ti，

(2)

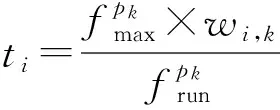
(3)

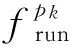
Tmakespan=AFT(nexit).

(4)

同样，根据文献[20]给出任务ni的向上排序值计算公式：

(5)

2.3能耗模型

根据文献[25,27]，有能耗

P=ACV2f,

其中,A代表芯片晶体管的平均开关数量，C为有效电容，V为供电电压，f为时钟频率.文献[25]中，将AC视作常数，本文沿用这一设定.

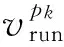
(6)

其中，ti可由式(3)求出.相应地，系统空载能耗的计算为

(7)

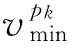
Etotal=Erun+Eidle.

(8)

2.4问题定义

本文要解决的问题是将工作流G中n个具有依赖关系的任务调度至k个异构的计算节点上并行运行，在满足时间约束的前提下使得G的整体能耗最小，形式化为

min(Erun+Eidle)，

s.t.Tmakespan≤Tdeadline,

其中,Tmakespan为工作流G的完成时间；Tdeadline为约束时间，由用户事先给出.同时，因降频导致处理时间延长，进而造成额外的能量消耗，不在本文讨论范围之内.

3算法描述及复杂性分析

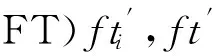
3.1算法描述

在给出本文算法描述之前，先来看一个DAG调度模型.为了更好地理解该算法，此处假设任务在处理器上的执行速度相同，详细数值由表1给出，表2为处理器的电压频率组.DAG模型由图1给出.

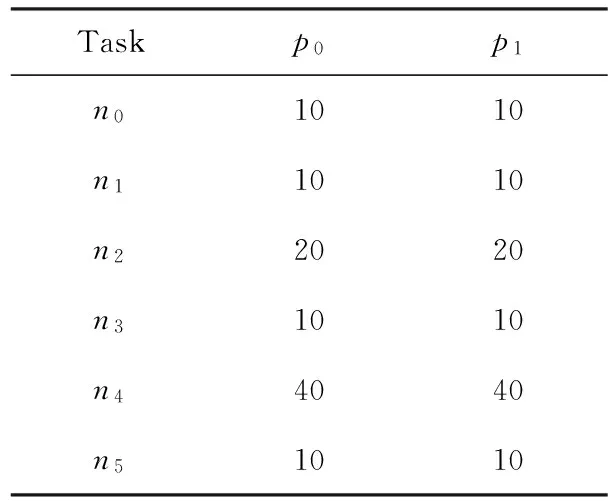
Table 1　Computation Cost

Table 2　Voltage and Frequency Pairs

表2　电压频率组

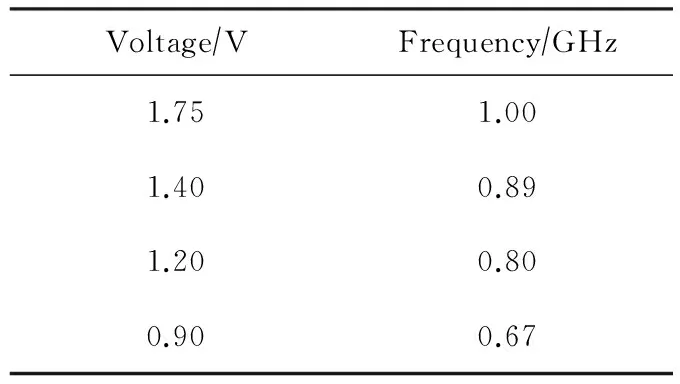
Table 2　Voltage and Frequency Pairs

Voltage∕VFrequency∕GHz1.751.001.400.891.200.800.900.67

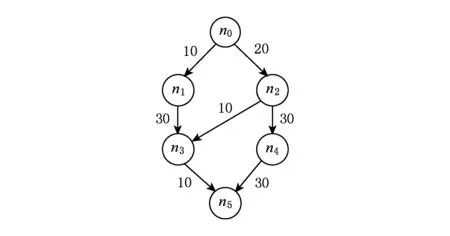
Fig. 1　An example DAG.图1　示例DAG

针对表1、表2和图1设定，使用HEFT算法生成该DAG的原始调度，可以得到Tmakespan=80，Etotal=339，如图2(a)所示.

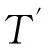
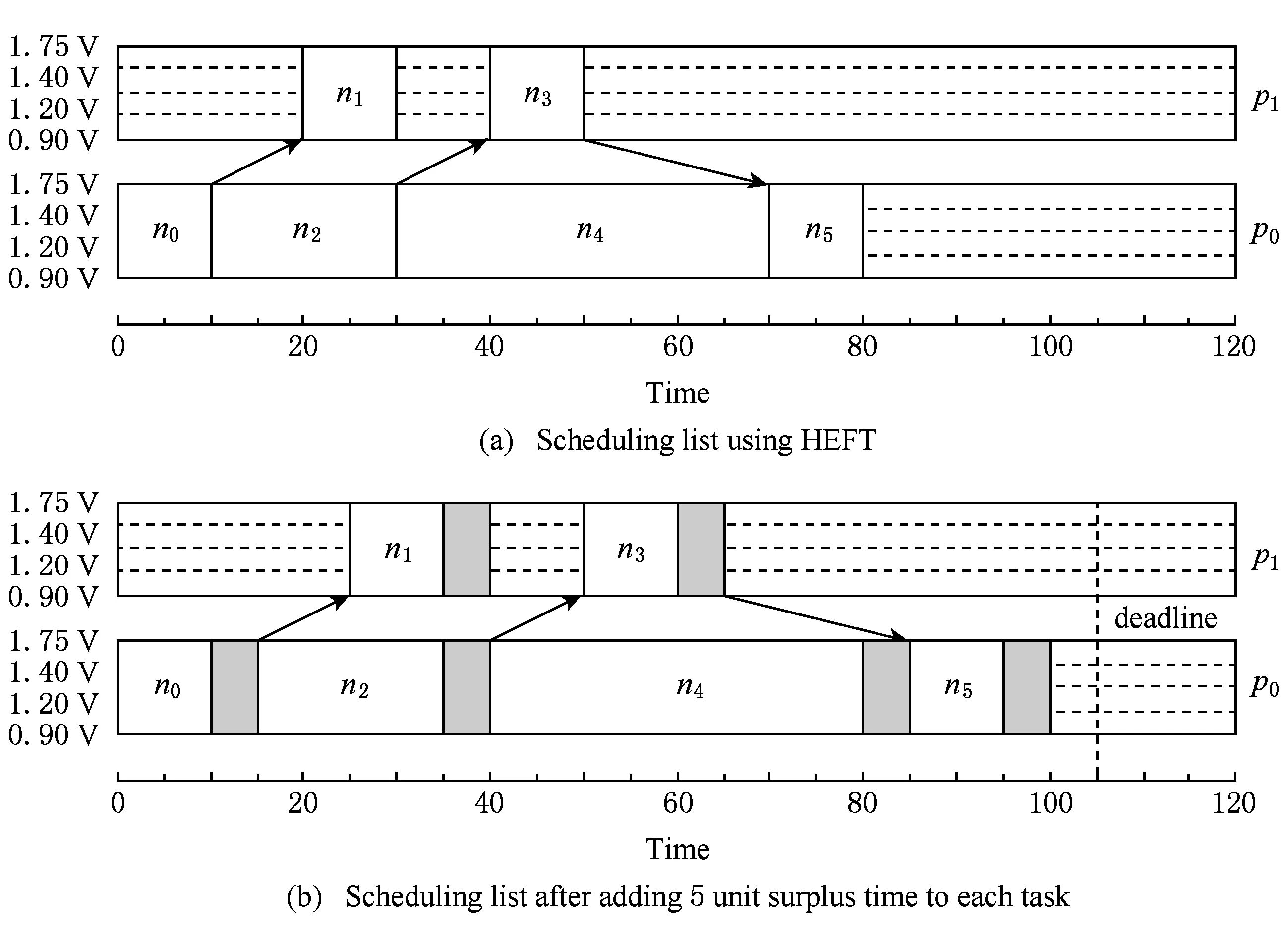
Fig. 2　Scheduling list of example DAG.图2　DAG调度图

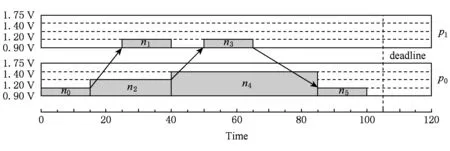
Fig. 3　Scheduling list after each task moderates to lower frequency.图3　各任务降频后的调度图

虽然示例DAG十分简单，但是它很清晰地表达了本文将要提出的算法的核心思想，即在原始调度的基础上逐步以不同的盈余时间值ΔS′同时增大各个任务的执行时间，之后在此基础上重新调度任务直至ΔS′=ΔS.需要引起注意的是，本文算法在任务重新调度过程中解除对处理器的限制，即任务可以在所有处理器及其对应的所有电压频率组上遍历搜索，从全局找寻能耗最优调度.

如何在盈余时间ΔS内找到最节能又满足时间约束的有效调度，最简单的方法是从下界完成时间Tlowerbound即(原始调度完成时间)开始，每次以最小搜索粒度譬如Δs=0.01(假设系统要求保留2位小数)递进累加，再在新生成的盈余时间ΔS′基础上对系统中的所有计算节点进行扫描，然后在m=ΔSΔs次遍历中找出合乎要求的调度.很显然，随着盈余时间的增大以及系统精度要求的提高，该算法时间复杂度会越来越高.经过大量的实验分析，当盈余时间根据系统精度要求以对应的最小搜索粒度譬如Δs=0.01进行递增时，m次遍历中存在大量的冗余调度.举例来说，使用文献[25]中的DAG设定，约束时间Tdeadline=95，在电压频率组V={(1.75,1.0),(1.40,0.8),(1.20,0.6),(0.90,0.4)}下，使用HEFT算法得到它的下界完成时间Tlowerbound=88，则在盈余时间ΔS=7内所有合乎要求的调度的盈余时间值与完成时间及运行能耗(不包含处理器空载能耗)对应关系如表3所示：

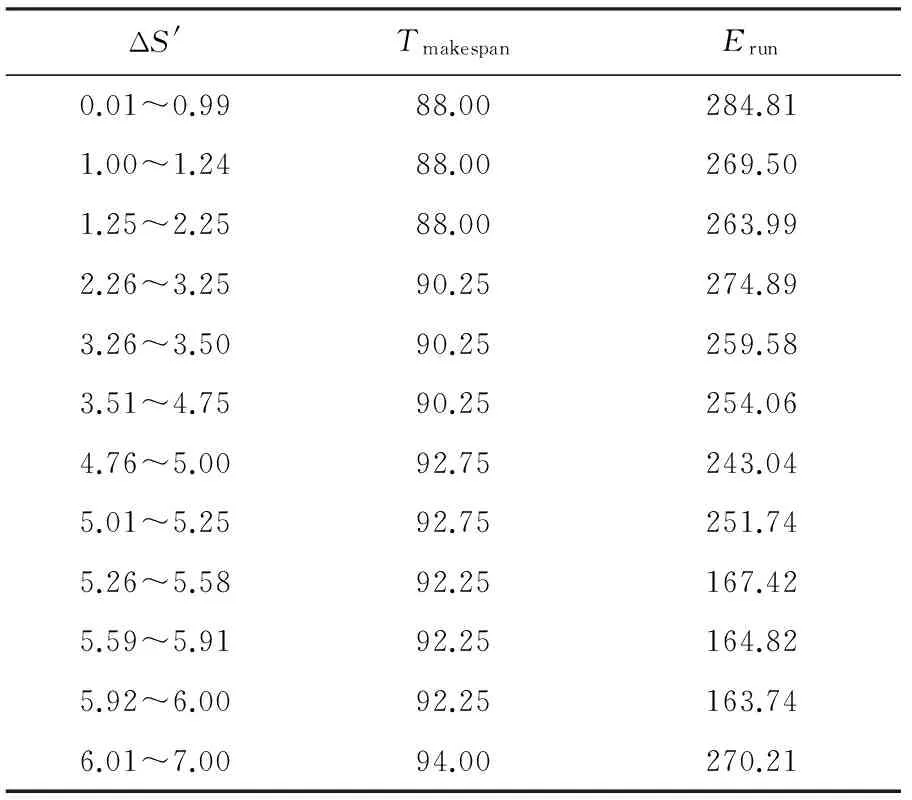
Table 3　The Correlation Between Surplus Time and Energy

从表3可以看出，当ΔS′∈[3.51,4.75]时，调度序列完全相同，这意味着在125次遍历中，有124次遍历生成的调度为冗余调度，如果能通过某种措施有效地去除遍历中的冗余调度，则算法时间复杂度将大幅降低.与此同时，从表3可以看出，所有有效调度中，运行能耗最小值为163.74，此时ΔS′∈[5.92,6.00]，这说明将最大盈余时间ΔS=7直接分配给各个任务并不能得到运行能耗最小的调度即运行能耗最优调度.但是盈余时间越大，可供选择的有效调度将越多.大量实验研究表明，以盈余时间ΔS的中点θ为分界点，则运行能耗最优调度其对应的盈余时间ΔS′将出现在[Tlowerbound+θ,Tdeadline]值域内.

由此，引申出算法的设计思想：取2个大小不同的搜索粒度：最小搜索粒度和最大搜索粒度，算法从最大盈余时间ΔS开始反向演算，直至盈余时间小于θ.每次演算均基于不同的搜索粒度取2个不同的盈余时间，再基于二者使用HEFT算法将工作流在所有处理器和电压频率组上遍历，得到2个有效调度(即既节能又满足时间约束的调度，如果这样的调度不存在，则以原始调度返回)，接下来基于2个有效调度能耗大小的判断结果设定下一轮演算的盈余时间与搜索粒度——即算法的核心思想是：在局部最优解的基础上重新指定搜索范围，期望以较小的时间复杂度、较快地接近全局最优解.过程类似自然界中青蛙的运动.

在给出算法的完整描述前，先给出相关定义：

定义1. 盈余时间.约束时间与下界完成时间的差值ΔS：

ΔS=Tdeadline-Tlowerbound≥0.

(9)

定义2. 蛙跳终点值.即搜索终点值，等于盈余时间ΔS的中点值，用θ表示:

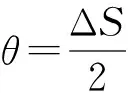
(10)

定义3. 最小跃度值和最大跃度值.每一次反向蛙跳时的跨度值，分别用Δsmin和Δsmax来表示.实质上，跃度值即为搜索粒度，为了更好地呼应算法，分别用此二值对应最小搜索粒度和最大搜索粒度.假设系统精度为ρ(即保留ρ位小数)，则：

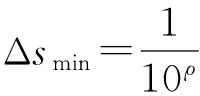
(11)

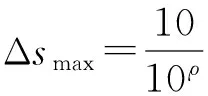
(12)

定义4. 盈余最早完成时间.任务ni的当前实际完成时间加上盈余时间ΔS′之后的时间:

EFT′(ni,ΔS′)=AFT(ni)+ΔS′.

(13)

定义5. 任务运行能耗.任务n在处理器p上以电压频率(vf)运行，在运行时间t内所产生的能耗:

Erun(n)=αv2f×t，

(14)

其中，t可由式(3)求得.

定义6. 最终可用调度.算法优化后的能耗最低调度用于工作流的实际调度，记为FSL.

算法完整描述如下：全称为反向蛙跳全局能耗感知算法(backward frog-leaping global energy conscious scheduling, BFECS)，共分为3个阶段：

1) 阶段1称为原始调度构造阶段，与文献[27-29]一样,利用HEFT算法求出DAG工作流原始调度及下界完成时间；

2) 阶段2为反向蛙跳全局扫描阶段，利用阶段1求得的下界完成时间，求得它与约束时间之间的盈余，通过反向蛙跳全局扫描，找出其中既使工作流运行能耗最小，同时又满足时间约束的最优调度(同样利用HEFT算法求得)；

3) 阶段3称为松弛时间回收阶段，在不破坏任务间依赖关系及不增加工作流运行完成时间的前提下，调整阶段2得到的运行能耗最优调度中任务的运行电压频率至更低的合适级别上，进一步降低DAG工作流的整体运行能耗.当约束时间等于下界完成时间即不存在盈余时间时，算法直接使用阶段3进行降能操作.

算法整体构造如下：

算法1. BFECS算法.

输入：DAG图G=(N,E,W,C)、可变电压处理器组P、电压频率组V；

输出：最终可用调度FSL.

① 利用算法2求得原始调度；

② 利用算法3求得运行能耗最优调度；

③ 利用算法4求得最终可用调度.

下面分阶段描述算法，阶段1为原始调度构造阶段.

算法2. 原始调度构造算法.

输入：DAG图G=(N,E,W,C)、可变电压处理器组P、电压频率组V、约束时间Tdeadline、系统精度ρ;

输出：原始调度SLorigin.

① 根据式(5)从出口任务开始自底向上计算出每个任务的向上排序值ranku(ni)；

② 对各个任务依据ranku(ni)降序排列，得到向上排序值降序任务列表TLdscranku；

③ 利用HEFT算法调度各个任务至合适的处理器上，每个处理器均运行在最高电压，即得到原始调度，记为SLorigin；

④ 对SLorigin使用式(4)求得Tmakespan，然后将其赋给Tlowerbound.

阶段2为反向蛙跳全局扫描阶段.

算法3. 反向蛙跳全局扫描算法.

输入:原始调度SLorigin、可变电压处理器组P、电压频率组V、向上排序值降序任务列表TLdscranku、下界完成时间Tlowerbound；

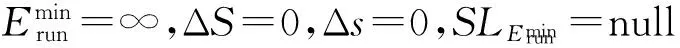
② ifTdeadline≤Tlowerbound

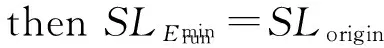
④ else

⑤ 根据式(9)计算盈余时间ΔS；

⑥ 根据式(10)计算蛙跳终点值θ；

⑦ 根据式(11)、式(12)计算最小跃度值Δsmin和最大跃度值Δsmax；

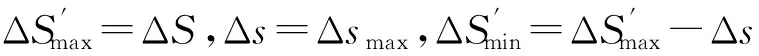
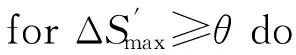
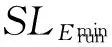
通过实验观察可知，算法阶段2得到的调度序列某些任务之间存在如文献[27-29]所描述的松弛时间，在不破坏任务间依赖关系的前提下，通过回收技术可以进一步降低DAG工作流的运行能耗.故算法阶段3称为松弛时间回收阶段.参照文献[27-29]，先给出一些相关描述知识.

针对某一任务ni，其最迟完成时间(latest finish time,LFT)的计算公式如下：

(15)

其中,tj表示任务运行时间;ci,j表示任务ni和nj之间的通信开销，如果ni与nj运行在同一处理器上，则通信开销ci,j=0.

任务的松弛时间计算为

Slack(ni)=LFT(ni)-AST(ni)-ti，

(16)

其中，AST(ni)表示任务ni的实际启动时间(actual start time, AST)，ti定义与式(15)中tj类同.

对潜在的任务进行降频操作即回收松弛时间之前，先计算出每个任务的LFT(ni)与Slack(ni)，接下来遍历向上排序值降序列表TLdscranku，每次从中选出队头任务ni，它运行在处理器pk上，如果Slack(ni)>0，则意味着ni的完成时间可以由之前的AFT(ni)变更为LFT(ni)，即ni的运行时间段可以被延长Slack(ni)个时间单位.在可变电压频率技术下，通过降低处理器的运行频率即可实现这一目的.假设任务ni完全消化掉松弛时间Slack(ni)时的最佳运行频率为fop，则：

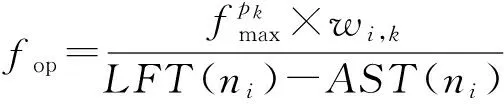
(17)

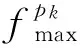
fnew=min(fl|fl∈Fpk,fl≥fop)，

(18)

其中,Fpk为处理器pk上的离散频率集.得到新的运行频率fnew后，进一步求得ni新的执行时间：

(19)

然后根据此时间更新任务ni的运行时间段，并将此更新保存下来.接下来需要对任务ni所有的直接前驱任务nj∈pred(ni)，以及与ni运行在同一处理器上的前紧邻任务np(如果存在)进行LFT和Slack更新操作，步骤依次为：

1) 针对ni的每1个直接前驱任务nj，首先计算出nj新的最迟完成时间LFT′(nj)：

tk-cj,k),AST(ndn(j))},

(20)

其中,tk,cj,k与式(15)中tj,ci,j定义类同.AFT(nk)为nj后继任务nk的实际完成时间；ndn(j)表示与任务nj处于同一处理器上且排在nj之后运行的第1个任务(如果存在)，如图2(a)所示，ndn(1)=n3，ndn(2)=n4.式(20)可以确保nj新的最迟完成时间LFT′(nj)小于或等于后紧邻任务的实际开始时间，目的是为了保证任务间依赖关系不被破坏.

2) 将LFT′(nj)代入式(16)后，可求得任务nj新的松弛时间Slack′(nj).

3) 同样地，针对与ni运行在同一处理器上ni的前一个任务，也称前紧邻任务np(如果存在)进行同样的LFT和Slack更新操作.以上更新操作执行完成后，将任务ni移出序列.重复以上过程直至任务序列为空.算法具体描述如下：

算法4. 松弛时间回收算法.

输出: 最终可用调度FSL.

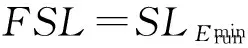
② 根据式(15)计算所有任务的最迟完成时间LFT；

③ forTLdscranku≠∅ do

④ 从TLdscranku取出任务ni；

⑤ 根据式(16)求得任务的ni松弛时间Slack(ni)；

⑥ ifSlack(ni)>0 then

⑦ 根据式(17)求得任务ni的最佳运行频率fop；

⑧ 根据式(18)求得任务ni的实际运行频率fnew；

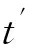
⑩ 更新任务ni的实际运行频率为fnew；

3.2算法复杂度分析

BFECS算法时间复杂度为O(m×p×v×e)，其中m为蛙跳次数，它与盈余时间ΔS、系统精度ρ正相关；p为处理器数；v为电压频率组数；e为DAG边数.

大量实验研究表明，满足时间约束的全局能耗最优调度，其完成时间接近约束时间，即此时算法尝试分配到各任务的盈余时间接近最大盈余时间.BFECS算法从约束时间开始反向搜索解空间，同时在搜索过程中基于返回结果与当前最优调度的判断，不断调整搜索粒度大小，期望以较快的速度找到最优调度.算法从最大盈余时间开始反向演算这一设计思想，能更快地找到最优解，提升算法收敛速度.

在算法每轮搜索中，总是将得到的调度与当前最优调度比较，如果新调度更有节能优势，则将它置为当前最优调度，否则保持当前最优调度不变.即算法在任何情况下均可以返回有效调度，算法是健壮的.

4实验结果与分析

4.1环境与样本设定

实验选取算法HEFT[20]，EES[27]，DEWTS[29]与BFECS进行比较，所有算法均用Java编写，实验环境为Windows 7 64 b，硬件配置为Intel Xeon E5-1603@2.80 GHz，4CPUs，16 GB RAM.

与文献[20,27,29]类似，实验使用随机DAG工作流来评估算法.通过随机设定DAG工作流的任务数、处理器数、计算开销、通信开销等参数，来模拟各种可能的并行工作流.具体为：任务数值域为n={20,40,60,80,100,120}.并行化因子值域为β={0.2,0.5,1.0,2.0,5.0}，该因子取值越大，则工作流并行度越高.通信计算比CCR的值域为ccr={0.1,0.5,1.0,2.0,5.0}，该比值越小，表示工作流为计算密集型，反之则为通信密集型.处理器数值域为p={4,8,16,32,64,128}.处理器异构因子值域为ε={0.2,0.4,0.5,0.6,0.8,1.0}，该值越小，系统异构性越不明显.约束时间Tdeadline与下界完成时间Tlowerbound的差值与T之比(时间差值因子)α={0.2,0.4,0.6,0.8,1.0}，系统精度ρ=2即保留2位小数.

同时，本文选取3个不同的具有DVFS功能的处理器作为实验设定之一[29]，它们的电压频率组值如表4所示：

Table 4　The Voltage and Frequency Pairs of Three Different Processor

表4　3种不同处理器的电压频率组

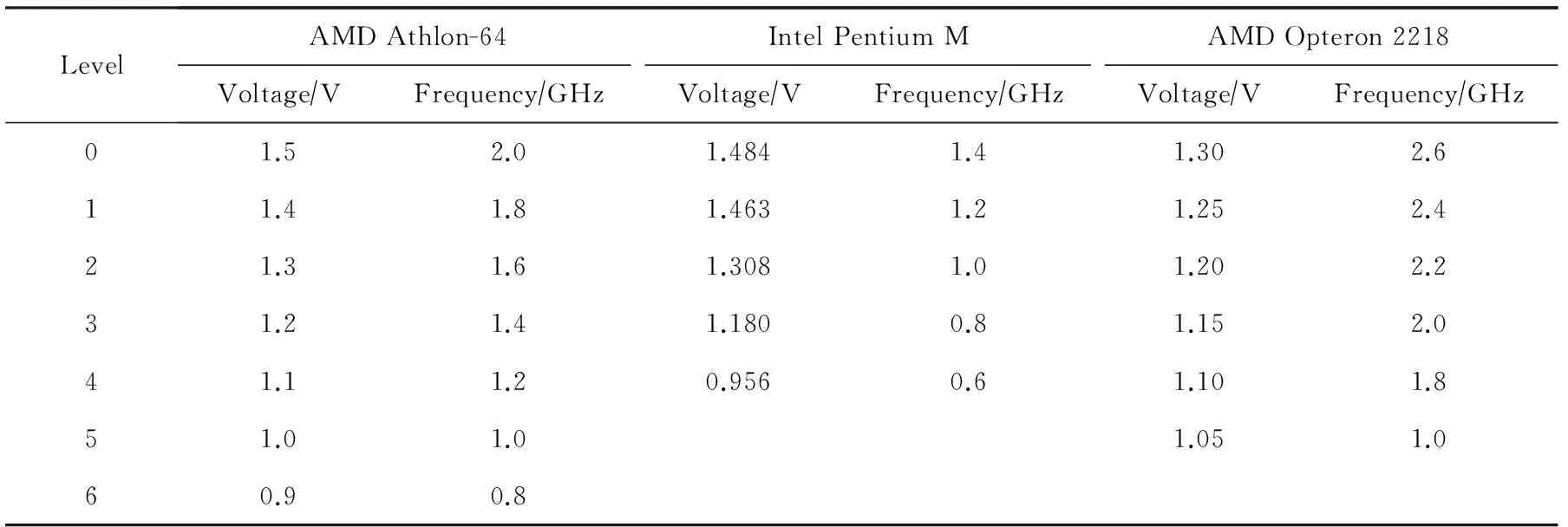
Table 4　The Voltage and Frequency Pairs of Three Different Processor

LevelAMDAthlon-64IntelPentiumMAMDOpteron2218Voltage∕VFrequency∕GHzVoltage∕VFrequency∕GHzVoltage∕VFrequency∕GHz01.52.01.4841.41.302.611.41.81.4631.21.252.421.31.61.3081.01.202.231.21.41.1800.81.152.041.11.20.9560.61.101.851.01.01.051.060.90.8

4.2评价指标

本文采用能耗比(energy consumption ratio,ECR)[15,29]和节能比(energy saving ratio,ESR)[29]作为评价指标，将提出的BFECS算法与HEFT，EES和DEWTS进行比较.其中DEWTS算法将无任务运行的空闲计算节点断电关机，被认为不合实际，因此针对该算法我们在实验中保持空闲计算节点的开启.

能耗比ECR的计算为

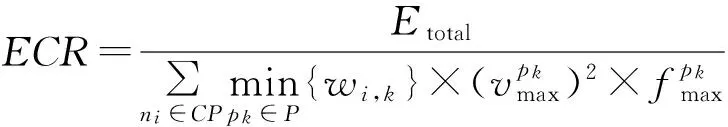
其中,分母为关键路径任务[20]CP在处理器pk(记使得关键路径任务完成时间最小的处理器为pk)上以最高电压频率运行时产生的运行能耗.约定在空闲阶段，处理器运行在最低电压频率以节能.Etotal为当前算法产生的整体能耗.

节能比表示约束时间内算法节约的能耗(即HEFT算法产生的能耗Ebase与当前算法产生的能耗Etotal之差)与Ebase的比值，它能直观地反应算法节能效率：

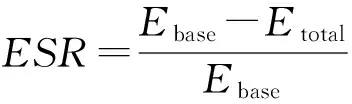
由此可以看出，只需将BFECS与EES，DEWTS两个算法比较即可.同样约定在空闲阶段，处理器运行在最低电压频率上以节能.

4.3实验结果及分析

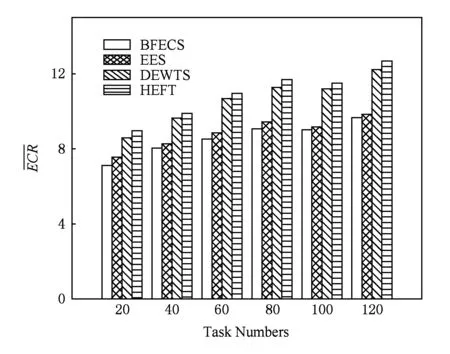
Fig. 4　Average ECR under different task numbers.图4　不同任务数下各算法能耗比

实验1. 比较各个算法在不同任务数下的ECR值.具体步骤为：固定其他参数(异构因子ε=0.5，并行化因子β=1.0，处理器数p=32，通信计算比ccr=0.5，时间差值因子α=0.2)，改变任务数，每个算法各运行1 000遍，然后取其ECR平均值.

从图4可以看出，在不同任务数下，BFECS算法能耗为HEFT算法能耗的77.5%～81.3%，DEWTS算法的79.7%～83.5%，EES算法的94.3%～98.3%，为4种算法中能耗最低的算法，且节能效率比较稳定.与其他3种算法不同，BFECS在所有计算节点上遍历，从所有有效调度中找出最节能的调度，因此它的节能效率得以较好保证.

实验2. 比较各个算法在不同处理器数下的ECR值.具体步骤为：固定其他参数(任务数n=40，异构因子ε=0.5，并行化因子β=1.0，通信计算比ccr=0.5，时间差值因子α=0.2)，改变处理器数，每个算法各运行1 000遍，然后取其ECR平均值.

从图5可以看出，随着计算节点的增多，各算法的能量消耗形势趋同明显.源于计算节点的增多导致潜在的空闲计算节点同时增多，空载耗能成为主要的影响因素.但在4种算法中BFECS算法仍然属于能耗最小的算法，在处理器数量可变情况下，BFECS算法能耗为HEFT算法的68.4%～93.2%，DEWTS算法的76.3%～94.1%，EES算法的88.9%～99.2%，算法节能效率明显且稳定.

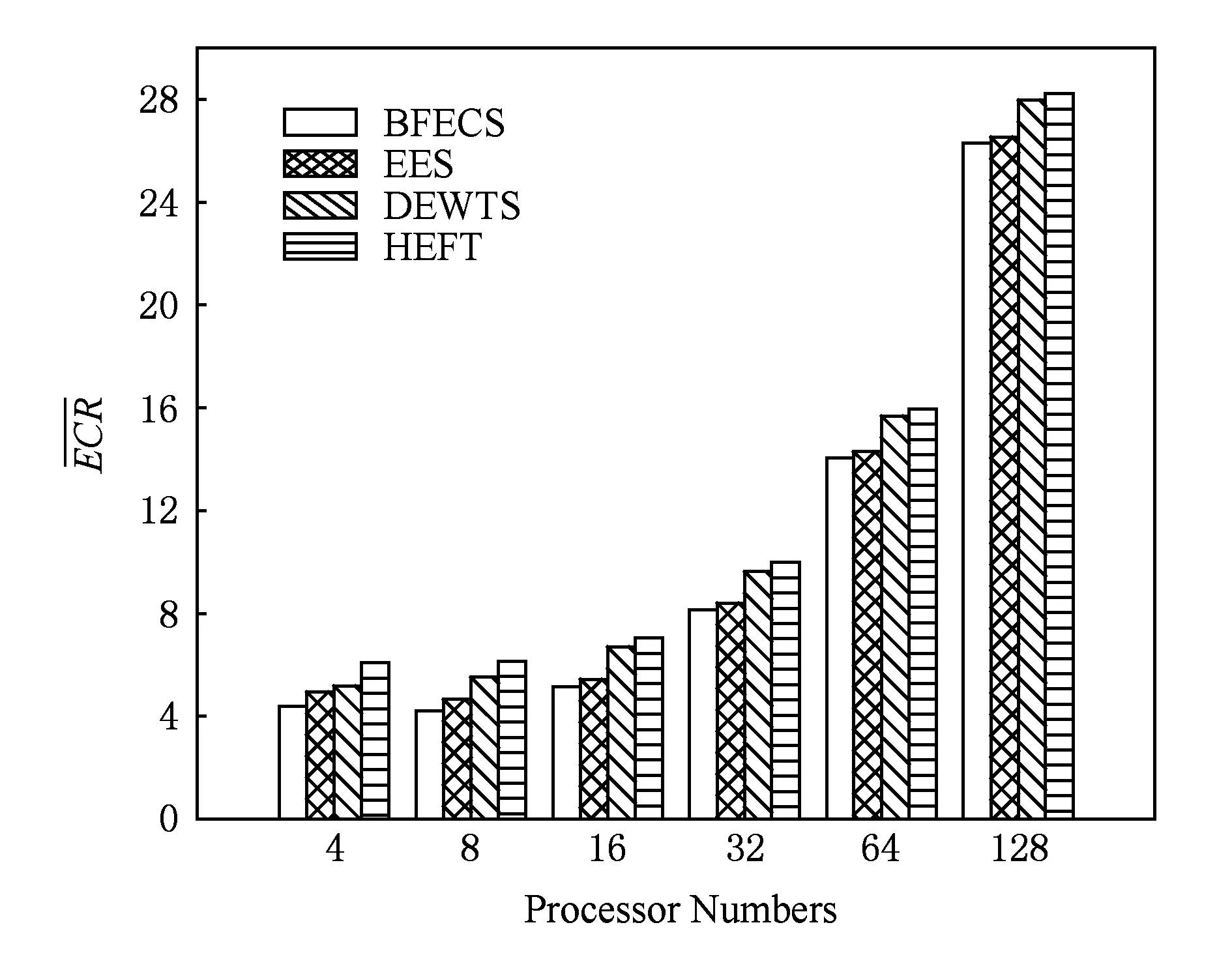
Fig. 5　Average ECR under different numbers of processors.图5　不同处理器数下各算法能耗比

实验3. 比较各个算法在不同约束时间下的ECR值.具体步骤为：固定其他参数(任务数n=60，处理器数p=32，异构因子ε=0.8，并行化因子β=2.0，通信计算比ccr=0.5)，改变时间差值因子，每个算法各运行1 000遍，然后取其ECR平均值.

图6中，随着时间差值因子的增大即约束时间的增大，BFECS算法的节能优势相对于EES算法逐步缩小.源于增大的盈余时间使得BFECS算法与EES算法同时给予各任务以更高的概率运行在处理器的低电压位上，因此两者能耗趋同明显.盈余时间的增大虽然有助于DEWTS算法以更大概率迁移任务至同一处理器上运行，但在大规模并行工作流中，增大的盈余时间不足以抵消高并行度所带来的影响，因此其节能效率逐渐被BFECS和EES拉开距离，与HEFT一起成为耗能较高的算法，并且当约束时间超过一定的范围之后，DEWTS算法中空闲计算节点越来越多，它逐渐超越HEFT算法成为最不节能的算法.反之，当时间差值因子减小时，BFECS算法节能优势较EES更为明显，如当α=0.4时它的能耗为EES算法的94.8%，当α=0.2时它的能耗为EES算法的83.1%.整体而言，BFECS算法在约束时间可变时，它的能耗约为HEFT算法的42.9%～58.4%，DEWTS算法的42.9%～66.1%，EES算法的83.1%～99.9%.

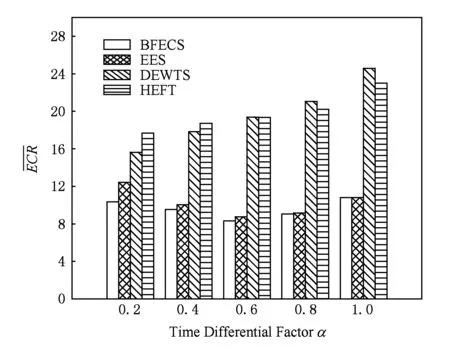
Fig. 6　Average ECR under different deadlines.图6　不同约束时间下各算法能耗比

实验4. 比较各个算法在不同处理器异构因子下的ECR值.具体步骤为：固定其他参数(任务数n=40，并行化因子β=2.0，处理器数p=32，通信计算比ccr=0.5，时间差值因子α=0.2)，改变处理器异构因子，每个算法各运行1 000遍，然后取其ECR平均值.

本组实验中，首先选取一个基准平均计算开销譬如说100，然后基于此值，根据不同的异构因子随机生成各任务在每个处理器上的计算开销，最终通过计算开销数值来体现处理器的异构性.从图7可以看出，BFECS算法在降低能耗方面恒定保有领先优势，为HEFT算法的59.9%～63.4%，DEWTS算法的66.6%～72.1%，EES算法能耗的91.3%～95.7%.从实验也可以看出，BFECS算法对系统异构性不敏感，节能效率比较稳定.

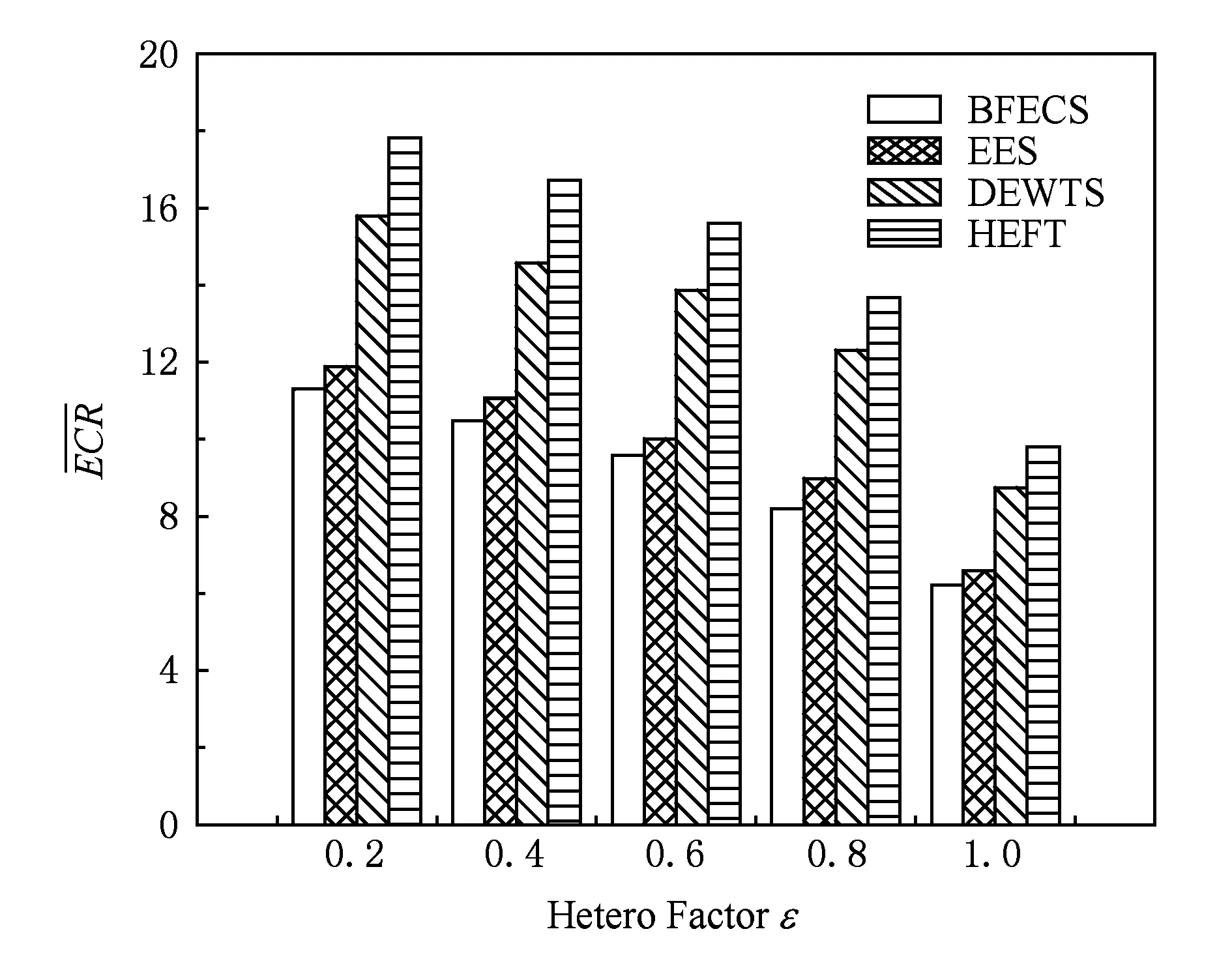
Fig. 7　Average ECR under different hetero factors of processors.图7　不同处理器异构因子下各算法能耗比

实验5. 比较各个算法在不同任务数下的ESR值.具体步骤为：固定其他参数(异构因子ε=0.5，并行化因子β=1.0，处理器数p=32，通信计算比ccr=0.5，时间差值因子α=0.2)，改变任务数，每个算法各运行1 000遍，然后取其ESR平均值.

从图8可以看出，不同任务数下，BFECS算法在节能方面比EES算法高出2.49%～30.2%，比DEWTS算法高出0.6～1.98倍，为3种算法中节能比最高的算法.任务数较少时，工作流运行能耗也小，在固定数量的计算节点上，BFECS算法从全局筛选出最节能的调度，此时节能比最高.随着任务数的增多，工作流运行能耗相应增大，在计算节点与时间差值因子固定的情况下，潜在能耗节约概率随之减小，此时BFECS算法与EES算法的节能比逐步接近，但BFECS仍为最节能的算法.

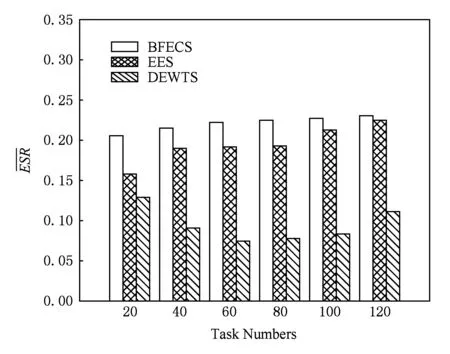
Fig. 8　Average ESR under different task numbers.图8　不同任务数下各算法节能比

实验6. 比较各个算法在不同处理器数下的ESR值.具体步骤为：固定其他参数(任务数n=40，异构因子ε=0.5，并行化因子β=1.0，通信计算比ccr=0.5，时间差值因子α=0.2)，改变处理器数，每个算法各运行1 000遍，然后取其ESR平均值.

从图9可以看出，随着计算节点的增多，节能比呈下降趋势，源于计算节点的增多导致潜在的空闲计算节点同时增多，空载耗能成为主要影响因素.整体而言，BFECS算法在节能方面比EES算法高出12.25%～47.5%，比DEWTS算法高出0.87～6.35倍，节能优势明显.在实验设定中，DEWTS算法由于不能关闭空闲计算节点，而是代之以最低电压频率空载运行，随着计算节点的增多它变得越来越不节能.

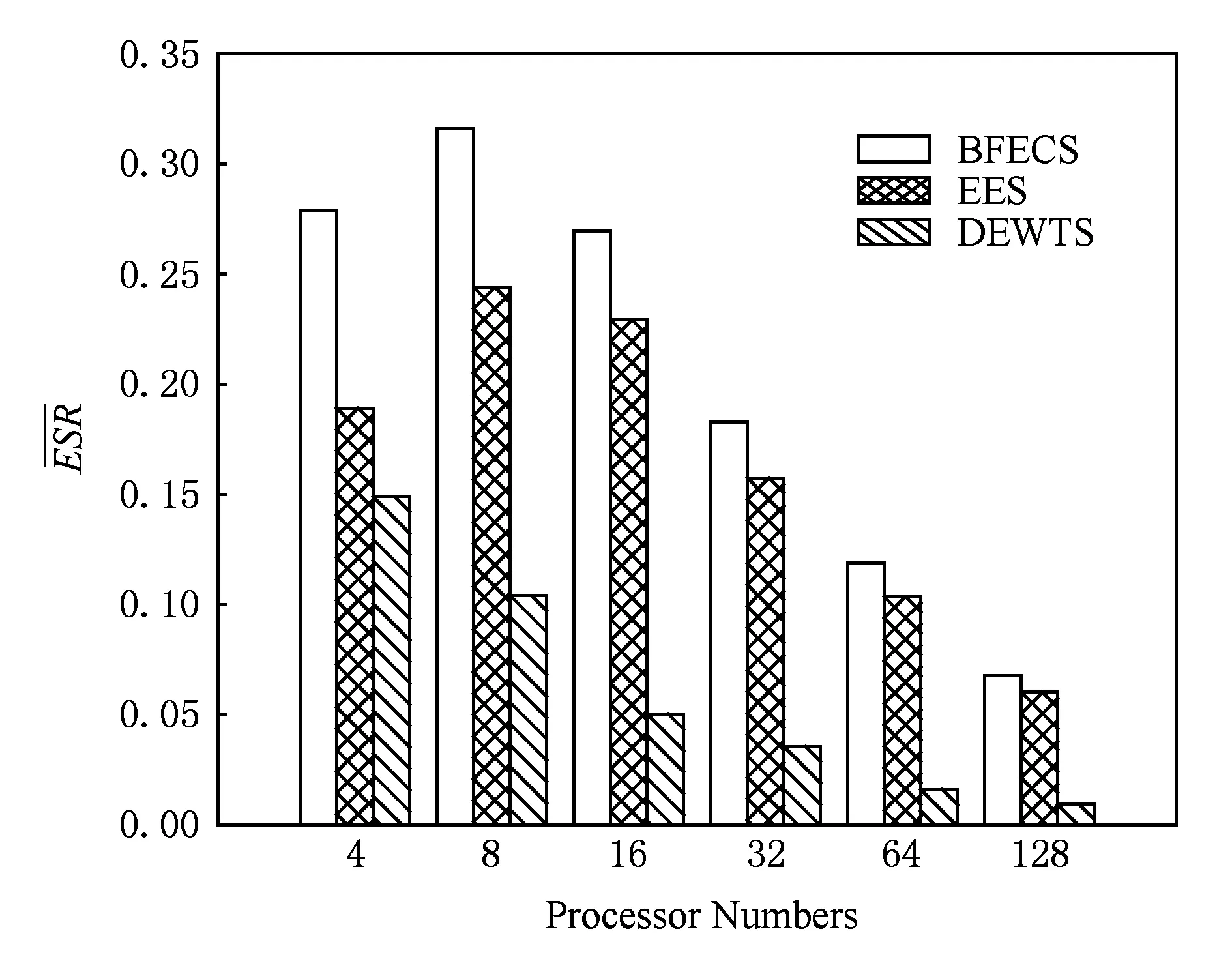
Fig. 9　Average ESR under different numbers of processors.图9　不同处理器数下各算法节能比

实验7. 比较各个算法在不同约束时间下的ESR值.固定其他参数(任务数n=60，处理器数p=32，异构因子ε=0.8，并行化因子β=2.0，通信计算比ccr=0.5)，改变时间差值因子，每个算法各运行1 000遍，然后取其ESR平均值.从实验3可以看出，当约束时间超过一定的范围之后，DEWTS超越HEFT成为最不节能的算法，势必导致本组实验中的节能比出现负数，因此，本组实验将时间差值因子限定在一个较小的取值范围，具体为α={0.1,0.2,0.3,0.4,0.5}.

从图10可以看出，当时间差值因子较小时，如α=0.1或0.2时，BFECS算法在节能方面，比EES算法高出28.1%～40.7%，比DEWTS算法高出1.15～3.02倍.当时间差值因子增大时，BFECS和EES两种算法在节能方面差距逐渐缩小，源于增大的盈余时间导致计算节点空载几率同步增大，空载能耗成为主要的影响因素.极端情况下，当约束时间足够大时，所有任务均运行在最低电压频率上，此时BFECS与EES在节能效率方面近乎相同.反观DEWTS算法，增长的盈余时间导致它的空闲计算节点越来越多，它变得越来越不节能，图10较好地印证了这点.

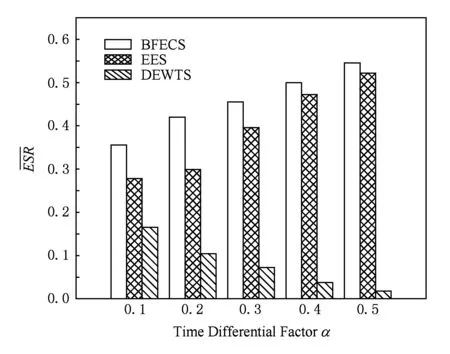
Fig. 10　Average ESR under different deadlines.图10　不同约束时间下各算法节能比

实验8. 比较各个算法在不同异构因子下的ESR值.固定其他参数(任务数n=40，并行化因子β=2.0，处理器数p=32，通信计算比ccr=0.5，时间差值因子α=0.2)，改变时间差值因子，每个算法各运行1 000遍，然后取其ESR平均值.

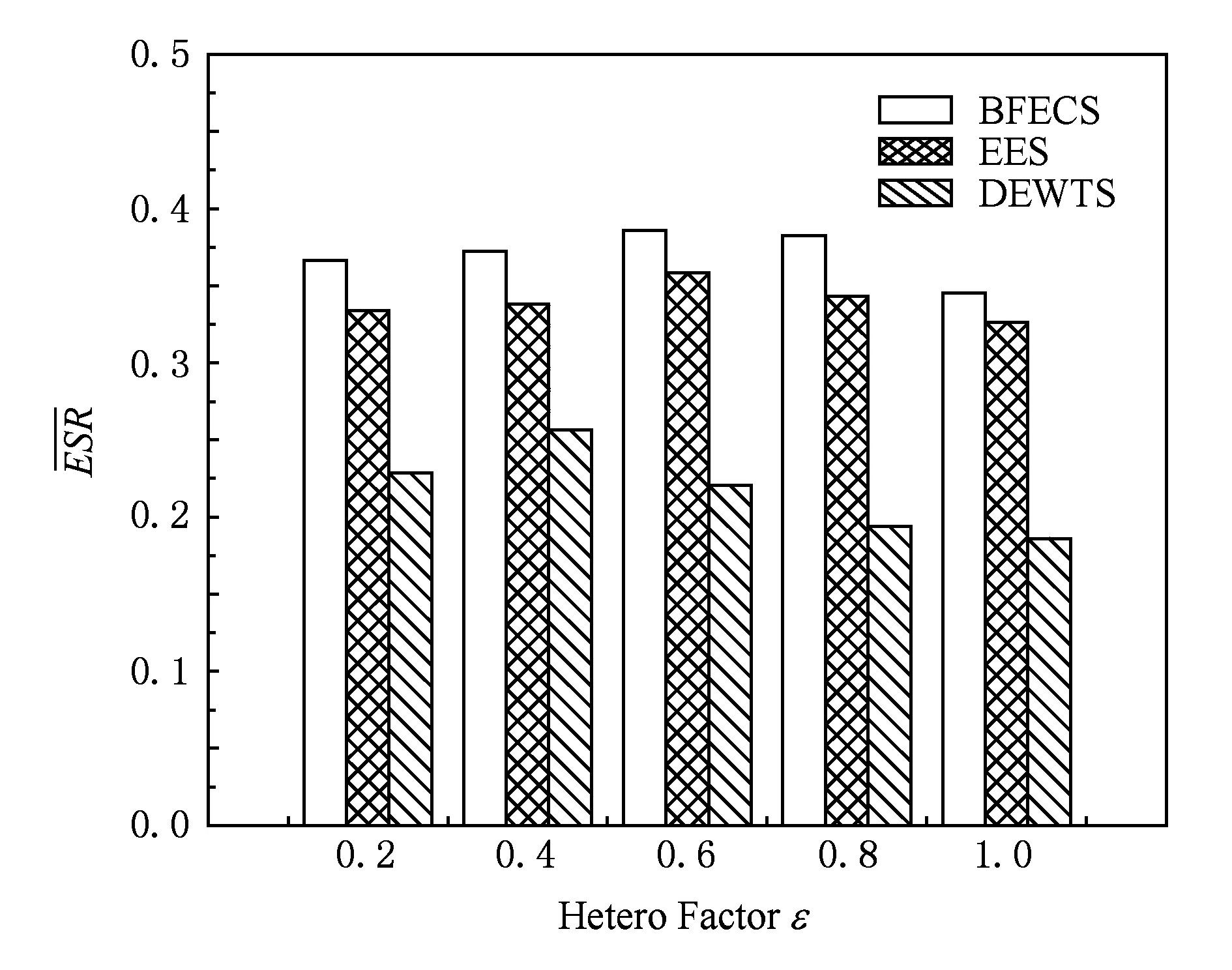
Fig. 11　Average ESR under different hetero factors of processors.图11　不同异构因子下各算法节能比

从图11可以看出，在异构因子的变化的情况下，BFECS算法持续保有较好的节能优势.整体而言，在节能比方面，它比EES算法高出5.8%～11.5%，比DEWTS算法高出45.1%～97.2%倍，为最节能之算法且对系统异构因素不敏感.

5结束语

本文利用DAG工作流下界完成时间与约束时间之间的盈余，引入最小跃度值和最大跃度值概念，提出了一种满足时间约束的能耗优化算法BFECS.与其他算法相比，BFECS总览全局，从所有可行调度中找出运行能耗最小的工作流调度，再利用松弛时间回收技术，在保持任务间依赖关系及满足工作流时间约束的前提下，调整任务的运行电压频率至更低但合适级别上，从而进一步降低DAG工作流的整体能耗.实验结果证实了BFECS算法的优越性.另外，该方法在实际应用中还有若干问题有待解决，如本文研究的是离线模型，未就任务执行时可能存在的“掉队”(straggler)情况进行考虑，因此，未来将该情况融入到离线模型中是一个非常有价值的研究问题.

参考文献

[1]Tanenbaum A S, Bos H. Modern Operating Systems[M]. Upper Saddle River, NJ: Prentice Hall, 2014

[2]Hwang K, Dongarra J, Fox G C. Distributed and Cloud Computing: From Parallel Processing to the Internet of Things[M]. San Francisco, CA: Morgan Kaufmann, 2013

[3]Fox G. Peer-to-Peer networks[J]. Computing in Science & Engineering, 2001, 3(3): 75-77

[4]Yang Guangwen, Jin Hai, Li Minglu, et al. Grid computing in China[J]. Journal of Grid Computing, 2004, 2(2): 193-206

[5]Zou Futai, Zhang Liang, Chen Shudong. Peer-to-peer network, grid computing and cloud computing—principles and security[M]. Beijing: Tsinghua University Press, 2012 (in Chinese)(邹福泰, 张亮, 陈曙东. 对等网络、网格计算与云计算——原理与安全[M]. 北京: 清华大学出版社, 2012)

[6]Amazon. Amazon Elastic Compute Cloud (EC2) [EBOL]. [2016-02-18]. http:www.amazon.comec2

[7]Google. Google App Engine [EBOL]. [2016-02-18]. http:appengine.google.com

[8]Apache. Hadoop [EBOL]. [2016-02-18]. http:hadoop.apache.org

[9]Apache. Spark [EBOL]. [2016-02-18]. http:spark.apache.org

[10]Wu Xindong, Zhu Xingquan, Wu Gongqing, et al. Data mining with big data[J]. IEEE Trans on Knowledge and Data Engineering, 2014, 26(1): 97-107

[11]Rao Lei, Liu Xue, Xie Le, et al. Coordinated energy cost management of distributed Internet data centers in smart grid[J]. IEEE Trans on Smart Grid, 2012, 3(1): 50-58

[12]Deng Wei, Liu Fangming, Jin Hai, et al. Harnessing renewable energy in cloud datacenters: Opportunities and challenges[J]. IEEE Network, 2014, 28(1): 48-55

[13]Greenberg A, Hamilton J, Maltz D A, et al. The cost of a cloud: Research problems in data center networks[J]. ACM SIGCOMM Computer Communication Review, 2008, 39(1): 68-73

[14]Deng Wei, Liu Fangming, Jin Hai, et al. Reliability-aware server consolidation for balancing energy-lifetime tradeoff in virtualized cloud datacenters[J]. International Journal of Communication Systems, 2014, 27(4): 623-642

[15]Zhang Longxin, Li Kenli, Xu Yuming, et al. Maximizing reliability with energy conservation for parallel task scheduling in a heterogeneous cluster[J]. Information Sciences, 2015, 319: 113-131[16]Wikipedia. Dynamic voltage scaling[EBOL]. (2016-01-06) [2016-02-18]. https:en.wikipedia.orgwikiDynamic_voltage_scaling

[17]Chandrakasan A P, Sheng S, Brodersen R W. Low-power CMOS digital design[J]. IEICE Trans on Electronics, 1992, 75(4): 371-382

[18]Wang Lizhe, Von Laszewski G, Dayal J, et al. Towards energy aware scheduling for precedence constrained parallel tasks in a cluster with DVFS[C]Proc of the 10th IEEE Int Conf on Cluster, Cloud and Grid Computing (CCGrid 2010). Piscataway, NJ: IEEE, 2010: 368-377

[19]Gerards M E T, Hurink J L, Kuper J. On the interplay between global DVFS and scheduling tasks with precedence constraints[J]. IEEE Trans on Computers, 2015, 64(6): 1742-1754

[20]Topcuoglu H, Hariri S, Wu M. Performance-effective and low-complexity task scheduling for heterogeneous computing[J]. IEEE Trans on Parallel and Distributed Systems, 2002, 13(3): 260-274

[21]Guoqi Xie, Liangjiao Liu, Liu Yang, et al. Scheduling trade-off of dynamic multiple parallel workflows on heterogeneous distributed computing systems[J]. Concurrency and Computation-Practice & Experience，2016, 1: 1-18

[22]Yuan Yingchun, Li Xiaoping, Wang Qian. Time optimization heuristics for scheduling budget-constrained grid workflows [J]. Journal of Computer Research and Development, 2009, 46(2): 194-201 (in Chinese)(苑迎春, 李小平, 王茜, 等. 成本约束的网格工作流时间优化方法[J]. 计算机研究与发展, 2009, 46(2): 194-201)

[23]Liu Cancan, Zhang Weimin, Luo Zhigang, et al. Workflow cost optimization heuristics based on advanced priority rule [J]. Journal of Computer Research and Development, 2012, 49(7): 1593-1600 (in Chinese)(刘灿灿, 张卫民, 骆志刚, 等. 基于改进优先级规则的工作流费用优化方法[J]. 计算机研究与发展, 2012, 49(7): 1593-1600)

[24]Liu Fangming, Zhou Zhi, Jin Hai, et al. On arbitrating the power-performance tradeoff in SaaS clouds[J]. IEEE Trans on Parallel and Distributed Systems, 2014, 25(10): 2648-2658

[25]Lee Y C, Zomaya A Y. Energy conscious scheduling for distributed computing systems under different operating conditions[J]. IEEE Trans on Parallel and Distributed Systems, 2011, 22(8): 1374-1381

[26]Li Keqin. Scheduling precedence constrained tasks with reduced processor energy on multiprocessor computers[J]. IEEE Trans on Computers, 2012, 61(12): 1668-1681

[27]Huang Qingjia, Su Sen, Li Jian, et al. Enhanced energy-efficient scheduling for parallel applications in cloud[C]Proc of the 12th IEEE Int Symp on Cluster, Cloud and Grid Computing (CCGrid 2012). Los Alamitos, CA: IEEE Computer Society, 2012: 781-786

[28]Su Sen, Huang Qingjia, Li Jian, et al. Enhanced energy-efficient scheduling for parallel tasks using partial optimal slacking[J]. The Computer Journal, 2015: 58(2): 246-257

[29]Tang Zhuo, Qi Ling, Cheng Zhenzhen, et al. An energy-efficient task scheduling algorithm in DVFS-Enabled cloud environment[J]. Journal of Grid Computing, 2016: 14(1): 55-74

[30]Fahringer T, Prodan R, Duan R, et al. ASKALON: A grid application development and computing environment[C]Proc of the 6th IEEE Int Workshop on Grid Computing. Los Alamitos, CA: IEEE Computer Society, 2005: 122-131

Jiang Junqiang, born in 1980. PhD candidate. Student member of China Computer Federation. His main research interests include cloud computing, parallel computing and resource scheduling.

Lin Yaping, born in 1955. Professor and PhD supervisor in Hunan University since 1996. Senior member of China Computer Federation. His main research interests include cloud computing, machine learning, network security and wireless sensor networks.

Xie Guoqi, born in 1983. PhD, postdoctoral researcher. Member of China Computer Federation. His main research interests include distributed systems, embedded systems, real-time systems (xgqman@hnu.edu.cn).

Zhang Shiwen, born in 1987. PhD candidate. His main research interests include security and privacy issues in social networks, cloud computing, sensor network, and data mining (shiwenzhang@hnu.edu.cn).

收稿日期：2016-03-10；修回日期：2016-05-12

基金项目：国家自然科学基金项目(61472125)

通信作者：林亚平(yplin@hnu.edu.cn)

中图法分类号TP393

Energy Optimization Heuristic for Deadline-Constrained Workflows in Heterogeneous Distributed Systems

Jiang Junqiang1,2, Lin Yaping1,2, Xie Guoqi1, and Zhang Shiwen1,2

1(CollegeofComputerScienceandElectronicEngineering,HunanUniversity,Changsha410082)2(KeyLaboratoryforDependableSystemandNetworksofHunanProvince(HunanUniversity),Changsha410082)

AbstractMost of existing energy optimization heuristics with deadline constraint for workflows in DVFS-enabled heterogeneous distributed systems usually trap in local optima. In this paper, we propose a new energy optimization heuristic called backward frog-leaping global energy conscious scheduling: BFECS. This algorithm makes full use of surplus time between the lowerbound of the workflow and the constrained deadline. Specifically, it starts from the constrained deadline, and leapfrogs towards the lowerbound of the workflow with different leap interval. During the whole process of leapfrogging, the leap intervals are continually changed according to the locally optimal value until the endpoint of leapfrogging is reached; the scheduling sequence with least run energy consumption is also saved at the same time. Furthermore, more energy consumption can be reduced by leveraging slack time reclamation technique, and the idle time slots caused by precedence constraints can be assimilated by the tasks through running at a lower and suitable voltage�frequency using DVFS technique, without violating the precedence constraints of the workflow and breaking the deadline. The experimental results show that the proposed algorithm can decrease energy consumption significantly.

Key wordsheterogeneous distributed systems; energy optimization; deadline constraint; workflow; slack time reclamation

This work was supported by the National Natural Science Foundation of China (61472125).