小滑块运动综合研究

陈 钺，柳建国（湖南理工学院 物理与电子学院，湖南 岳阳 414006）

小滑块运动综合研究

陈 钺，柳建国
（湖南理工学院 物理与电子学院，湖南 岳阳 414006）

系统研究了小滑块在光滑平面上滑动的过程，指出通常经典研究方法中所采用的纯滑动物理过程模型存在缺漏： 当滑块越过二面角棱线时，其发生运动状态剧变，必须补充一“完全非弹性斜碰”物理过程模型来描述方可，机械能也不再守恒了.

光滑； 二面角； 碰撞； 动量定理； 物理过程模型

小滑块在平面上滑动是最常见的物理模型，有必要系统的深入综合研究、探讨.

如图1所示： 实验室光滑水平面上固定两光滑斜面（0＜θ＜，0＜φ＜）. 在左侧斜面上高H处静置一质量为m的■小滑块，试求该滑块自由下滑到水平面时的速度v. 并分析其在右侧斜面可上升的最大高度h.

这是一个滑块运动的常规综合问题，早已有常规经验求解方法：

采用纯滑动物理过程模型，滑块运动过程仅保守内力（重力）做功，故机械能守恒. 取水平面为重力势能零点参考处，滑块运动则是重力势能与动能的相互转换过程，故遵循机械能守恒定律：

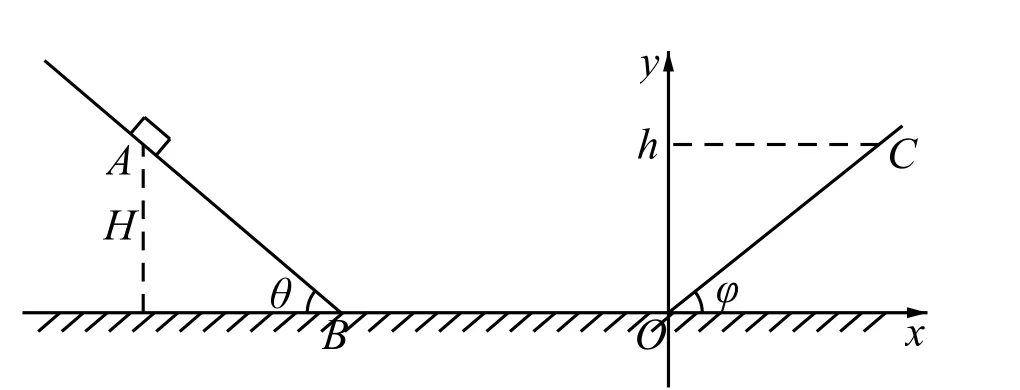
图1

对于常规最经典的物理问题，我们有必要深入探讨、研究，因为所谓经验，很可能是一个陷阱，其左右我们的判断.

小滑块平动，可采用质点模型描述，本文称其为质点.

（1） 质点在重力作用下加速下滑，机械能守恒： 如图1所示，在A点处，Eg=mgH，EK=0； 到达B

1 常规经验求解过程分析考查

（2） 质点离开B点处沿光滑水平面匀速直线运动，设其速度为v，机械能守恒，则22mumv=. 所以==.

2 经典常规求解方法中存在于物理过程模型中的缺陷

文[1，2[分析了其不合理性，并用实验证实： 质点在B点处与水平面发生了一次完全非弹性斜碰后，以速度cos离开B点匀速直线运动. 故滑块在水平面上运动速度应为v

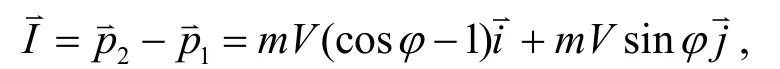
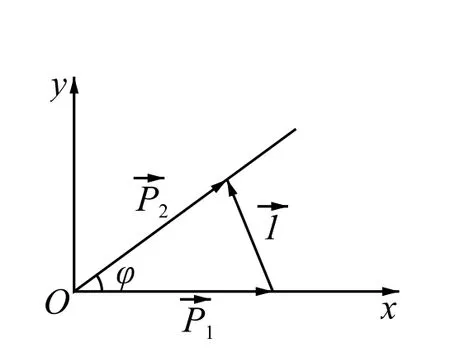
图2

3 从新角度探讨质点在O点处运动状态的剧变过程

应用运动叠加原理，质点进入O点时，将其运动分解为两个分运动： 沿斜面方向以速度cosVφ运动和 在垂直于斜面方向以速度sinVφ运动，这样两个分运动，如图3所示. 分析、探讨其在光滑斜面约束下运动状态的改变.

（1） 设质点离开O点时，沿斜面方向的运动速度为1u，而垂直于斜面方向运动速度为2u.

（2） 沿光滑斜面方向： 光滑斜面对质点运动无影响，而从进入O点到离开O点质点行程趋于零，重力做的功也趋于零，故质点离开O点时开始沿斜面方向运动速度依然为

（3） 垂直于斜面方向上，质点与斜面发生碰撞，因滑块并无跃起现象，其必为完全非弹性碰撞，故质点离开O点时u2=0.

（4） 合成上两分运动可知： 质点在水平面与右侧斜面所组成的二面角的棱线处发生了一次完全非弹性斜碰，损失了部分机械能，而以速度u1=Vcosφ 离开O点沿右侧斜面向上滑动，仅具动能mV2cos2φ.

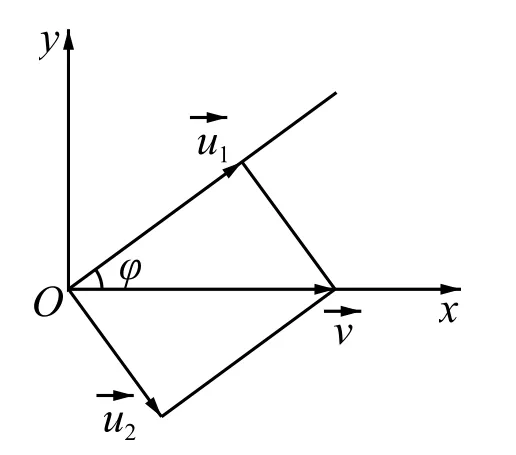
图3

4 小滑块运动的五个物理过程

（5） 小滑块离开O点以速度u1=2gHcosθcosφ 开始沿右侧斜面向上滑动，具有初态动能Ek. 当动能完全转换为重力势能Eg=mgh时，停止上升而到达可上升最大高度h，从而有

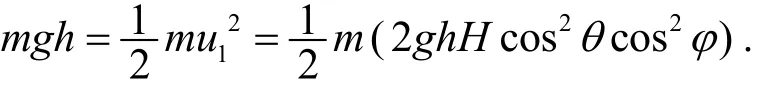
由上述分析、研究可总结出一普遍规律：

当滑块滑过由两平面形成的二面角棱线时，运动状态发生的剧变是因为发生了一次完全非弹性斜碰而产生的，损失了部分机械能，故机械能不再守恒. 机械能守恒定律不再适用了，相对于经典常规求解过程所采用的纯滑动物理过程模型，应补入一个完全非弹性斜碰的物理过程模型以描述该运动状态剧变过程.

5 非常规二面角上小滑块运动综合研究

研究小滑块滑动，总离不开“水平面”或“水平线”以提示滑块是否可能沿某平面滑动，两平面组成的二面角大于并小于π时，滑块可越过棱线滑动，前面已讨论、探讨过了，但还存在如下几种类型：

图4

图5

（3） 如图6所示，若0＞φ＞-ffff58π，则两平面组成的二面角大于π而小于ffff57π，则滑块越过棱线作平抛运动，与右侧斜面发生完全非弹性斜碰后再沿斜面滑动，机械能依然不守恒.

图6

我们全面讨论了滑块沿平面滑动的各种类型，在能越过二面角棱线继续滑动的情况中，滑块恒发生完全非弹性碰撞现象，机械能恒不再守恒，故在研究滑块运动时，机械能守恒定律的应用，应小心、注意方可.

继拙文[1，2[后，本文完成了对小滑块运动的系统、综合探讨和分析，结论是：

滑块越过二面角棱线时，必须在经典常规求解方法所建立的纯滑动物理过程模型中补入完全非弹性斜碰的物理过程模型，以描述其运动状态的剧变，机械能守恒定律不再适用.

[1]陈 钺，柳建国. 小滑块运动再研究[J[. 湖南理工学院学报，2014，27（3）： 26～27

[2]陈 钺，柳建国. 小滑块在非光滑平面上运动再研究 [J[. 湖南理工学院学报，2015，28（4）： 20～22

[3]程守诛，江之永. 普通物理学[M]. 第6版. 北京： 高等教育出版社，2006

Comprehensive Study of Small Slider Movement

CHEN Yue，LIU Jian-guo
（College of Physics & Electronics，Hunan Institute of Science and Technology，Yueyang 414000，China ）

This paper conducted a systematical and comprehensive study on the sliding movement of small slider on smooth surface. It pointed out that the pure physical process model of sliding activity employed in classical research methods is flawed. When the slider moves across the ridge line of dihedral angle，drastic changes are generated in its state of motion. A completely oblique inelastic collision process model must be supplemented to describe the physical activity，and the mechanical energy conservation no longer exists.

smooth，dihedral angle，collision，momentum theorem，process model of physical activity

O313

A

1672-5298（2016）02-0013-03

2015-12-03

陈 钺（1947- ），男，江苏吴锡人，湖南理工学院物理与电子学院副教授. 主要研究方向： 电磁场理论、物理教育