Bloch流动方程在分析磁共振血流信号中的应用

苏 晋，袁小燕（长治医学院 基础医学院，山西 长治 046000）

Bloch流动方程在分析磁共振血流信号中的应用

苏 晋，袁小燕
（长治医学院 基础医学院，山西 长治 046000）

磁共振成像理论研究中，Bloch方程常用来求解自旋核的动力学行为. 对于流动质子情况磁共振信号的描述则可以利用流动Bloch方程. 本文在具体的物理模型中，利用Bloch流动方程，分析了血液的流速及不同的射频场条件下，磁共振信号的变化. 结果显示，相同条件下，质子流速较快时会减弱信号，而在非线性的射频场条件下，磁共振信号会减弱. 理解不同条件下磁共振信号的变化，对于磁共振成像技术的研究和改进提供了理论参考.

磁共振成像； Bloch方程； 磁共振信号； 血液流动

引言

磁共振成像是医学成像中常用的一项技术，涉及诸多学科，如数学、基础物理以及工程技术等. 磁共振成像不仅有助于组织形态和疾病状态的诊断，也是功能性成像的重要方法. 比如，扩散成像、流动成像、 灌注成像、血管造影、化学位移成像、脑功能成像等. 在临床应用中，了解其物理机制对于理解和改进成像方法，正确的图像质量评价等有着重要的意义. 而其中最基本的关于磁共振信号的描述就是Bloch方程，一般在教科书里提到的Bloch方程只是对静止的自旋核所产生的磁化强度矢量的动力学描述，如何利用Bloch方程求解动态模型下的自旋核的动力学行为成为一个研究方向. 本文从Bloch方程的一般形式出发，引出Bloch流动方程的一般形式，在设定好的初始条件和给定的流动模型下，讨论了血管中氢质子流动对磁共振信号的影响，希望能够利用Bloch流动方程的方法，为磁共振成像的理论研究提供一种动力学机制.

1 磁共振成像中的流动Bloch方程

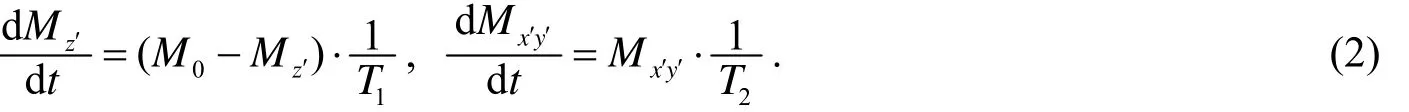
分别表示z方向和xy方向磁化强度矢量随时间的变化.

同时考虑到上面两个因素，Bloch方程可以表述为[5］

对式（3）进行x方向的偏微分可得

xyz1示x方向质子的流动速度.

方程组（4）为Bloch流动方程的一般形式[6～10］，它为描述流动对象的磁共振信号变化提供了理论基础.

2 流动模型的建立和Bloch方程的应用讨论

方程组（4）的精确求解一般情况下较为复杂. 本文建立了一小段简化的血管模型进行讨论. 在这个模型中，设外部静磁场B0沿着z方向，为主动脉方向. 信号检测取自y方向. 在热平衡状态下，模型所描述的系统有一个沿着z方向的磁化强度矢量M0.

为了讨论问题方便，选择了与实际情况接近的初始条件： （1） 射频场B1（x）比较强时Mz≠M0； （2） 线圈接收信号之前，横向磁化强度矢量Mx=0，My=0.

当血液稳定流动时，假设其速度为V，讨论一种特殊的情形，即稳定流动情况. 此时，由=0，可得到求解磁共振信号的表达式[11，12］：

这是磁共振流动Bloch方程的在设定好的初始条件下的求解方程. 关于Bloch流动方程求解的更一般形式在文[8[中也进行了讨论.

3 数值计算及结果分析

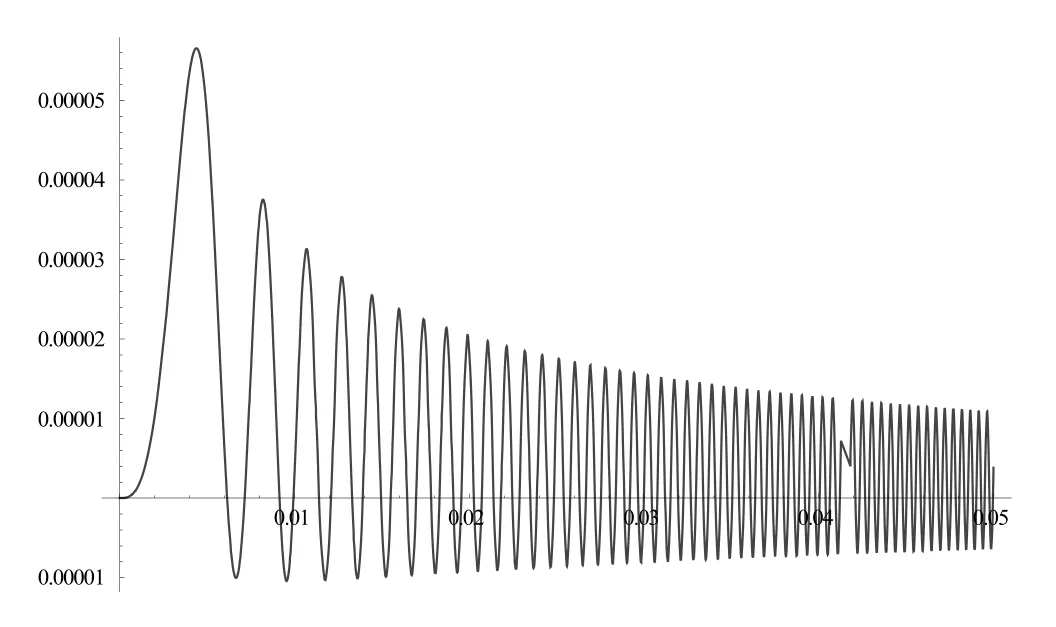
图1 V = 1m/s时，血管中磁共振信号的变化趋势图

为了讨论模型中的血液流动情况对对磁共振信号的影响，如流速对信号的影响，以及射频场1（）Bx不同对磁共振信号带来的影响，包括稳定的、线性和非线性的射频场对信号的影响，本文采用了数值分析的方法，结合特定的初始条件和模型，对方程（5）进行了求解和分析.

3.1 Bloch方程对流动模型下磁共振信号的求解 结合本文中的模型，设定血液流动的速度

为1m/s，纵向驰豫时间T1为2.0s； T2为0.2s； B1场设为线性场即B1（x）=0.001x，单位T； 可以得到如图1所示的结果.

从图1中可以看到，在x方向一个小的范围（0～5cm）内，磁共振信号振荡衰减，表现形式与FID（自由感应衰减信号）相似.

图2 V = 0.6m/s时血管中磁共振信号的变化趋势图

在相同的条件下，改变血液流动的速度，分别取V = 0.8m/s、0.6m/s、0.4m/s和0.2m/s，均可以得到相应的变化情况. 图2表示的是V=0.6m/s 时的血管中磁共振信号的变化趋势图. 从趋势图中可以看出，不同流速下（均为稳定流动）磁共振信号趋势相同，为振荡衰减，而流速较快的情况中，相同时间时磁共振的信号较弱，随着速度的减慢，磁共振的信号开始增加. 分析其原因，是由于流动的质子改变了质子周围的磁场环境，增加了磁场不稳定性因素，加快了横向弛豫过程，信号有所减弱.

3.2 B1场的选择对流动模型下的磁共振信号的影响

射频场是产生磁共振的重要条件. 磁共振成像中，射频场的选择根据需要有不同的形式，如线性场（B1（x）=ax+b），非线性场（B1（x）=ax2+bx+c），或者常数场（B1（x）=const ）. 以下讨论了B1场对磁共振信号的影响.

3.2.1 稳定射频场对流动质子磁共振信号的影响

当B1场为常数（设为0.00006mT），其它参数同上，在x方向较短的范围内，得到结果如图3所示. 由图3可知，随时间和坐标不变的射频场，将带来磁共振信号在连续空间上的振荡稳定，当然，随着流速的不同，这种振荡程度将会不同. 图4为相同条件下，流速为0.6m/s下的磁共振信号变化情况.

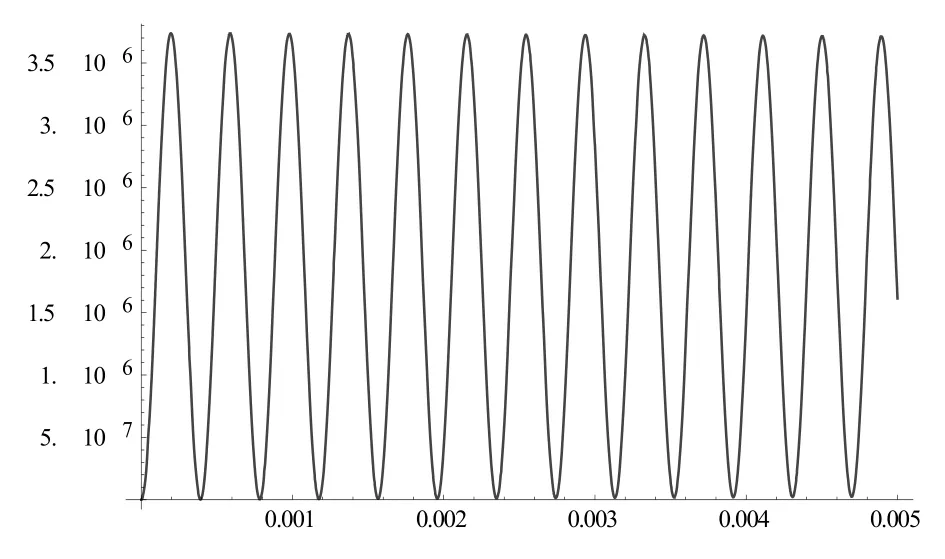
图3 V = 1m/s时血管中磁共振信号的变化

图4 V = 0.6m/s时血管中磁共振信号的变化

图5 非线性射频场下磁共振信号的变化规律

比较图3和图4可知，流速降低使得磁共振信号的振荡频率提高，或者说磁共振信号的频率与血液在x方向的流动情况相关，这为血液流动的分析提供了理论上的参考价值.

3.2.2 线性和非线性射频场对磁共振信号的影响分析 线性B1场（B1（x）=0.001x）对磁共振信号的影响在图1中已有所讨论. 若射频场调制为非线性场，这里取 B1（x）=0.001（x2+2x），通过数值计算和分析可以得到如图5所示的结果.

在非线性的B1场下，磁共振信号随着空间坐标x的变化表现为振荡衰减的形式，与图1中的线性B1场趋势相同. 有所改变的是磁共振信号的幅度. 与线性场相比，非线性场下，磁共振信号幅度较小. 从图5中可以看到，尽管采用了不同的射频场形式，射频场的幅度本身有所不同，但总的来说，在非线性的射频场下，磁共振的信号幅度有所减弱. 这是由于非线性的射频场下，质子所处磁场环境的不均匀性增加，加剧了xy平面内的相位扩散.

4 结束语

本文利用流动Bloch方程，通过对血管简化模型中流动质子的动力学分析，分析了流速和不同的射频场条件下磁共振信号的变化规律，结果发现，流动速度的快慢影响到磁共振信号的幅度，同时，非线性的射频场增加了磁场的不均匀性，也会对磁共振信号造成衰减.

磁共振成像中Bloch方程的应用，不仅可以描述静态自旋核的动力学行为，对流动模型下的自旋核同样适用. 运用流动Bloch方程进行分析和求解时，精确计算尽管较为复杂，但可通过数值计算的方法，对流动质子对具体模型下磁共振信号的影响规律进行初步分析和讨论，能对复杂的模型和临床环境下具体情况的分析提供部分理论基础.

[1]包尚联. 现代医学影像物理学进展[M[. 北京： 北京大学出版社，2014

[2]俎栋林. 核磁共振成像学[M[. 北京： 高等教育出版社，2004

[3]俎栋林，高家红. 核磁共振成像—物理原理和方法[M[. 北京： 北京大学出版社，2014

[4]Hendee W R，Ritenour E R. Medical imaging physics[M[. Wiley-Liss，2002

[5]Bushberg J T，Seibert J A，Leidholdt E M，et al. The essential physics of medical imaging [J[. third edition Medical Physics，2013，40（7）： 077301

[6]Awojoyogbe O B. A mathematical model of the Bloch NMR equations for quantitative analysis of blood flow in blood vessels with changing cross-section-I [J[. Physica A Statistical Mechanics & Its Applications，2002，303（s 1-2）： 163～175

[7]Awojoyogbe O B. A mathematical model of Bloch NMR equations for quantitative analysis of blood flow in blood vessels of changing cross-section—PART II[J[. Physica A Statistical Mechanics & Its Applications，2003，323（5）： 534～550

[8]Awojoyogbe O B，Boubaker K. A solution to Bloch NMR flow equations for the analysis of hemodynamic functions of blood flow system using m-Boubaker polynomials[J[. Current Applied Physics，2009，9（1）： 278～283

[9]Awojoyogbe O B，Dada O M，Boubaker K，et al. Flow Dynamics in Restricted Geometries: A Mathematical Concept Based on Bloch NMR Flow Equation and Boubaker Polynomial Expansion Scheme[J[. Journal of Applied Mathematics & Physics，2013，01（5）： 71～78

[10]Awojoyogbe O B，Dada O M，Physics D O. Mathematical design of a magnetic resonance imaging sequence based on bloch NMR flow equations and bessel functions[J[. Chinese Journal of Magnetic Resonance Imaging，2013，5（1）： 373～381

[11]Pitts D，Sissom L E. Schaum's Outline of Heat Transfer[M[. Mcgraw-Hill Publ.Comp.，2011

[12]Awojoyogbe O B，Faromika O P，Dada M，et al. Mathematical Models of Real Geometrical Factors in Restricted Blood Vessels for the Analysis of（Coronary Artery Diseases） Using Legendre, Boubaker and Bessel Polynomials[J[. Journal of Medical Systems，2011，35（6）： 1513～20

Application of Bloch Flow Equation in Analysis of Blood Flow in Blood Vessels

SU Jin，YUAN Xiao-yan
（Basic Medical College，Changzhi Medical College，Changzhi 046000，China）

Bloch equation is used to solve the dynamics behavior of nucleus in magnetic field，and the physics mechanisms of blood flow can be described by Bloch flow equation. We discussed the influence of MR （Magnetic Resonance） signal under specified conditions with different parameters such as blood flow velocity and RF（Radio Frequency） field. It showed that high velocity and nonlinear RF filed will weaken the signal. Understanding change of MR signal under a variety of conditions will help to better develop MRI （Magnetic Resonance Imaging） technique and provide theoretical reference for MRI.

magnetic resonance imaging，Bloch equation，MR signal，blood flow

O571.22

A

1672-5298（2016）02-0058-04

2016-03-10

苏 晋（1980- ），男，山西长治人，硕士，长治医学院基础医学院讲师. 主要研究方向： 理论物理，医学影像物理