时间序列平稳性分类识别研究

管河山 ，邹清明 ，罗智超

(1.南华大学 经济管理学院,湖南 衡阳421001；2.厦门大学 王亚南经济研究院，福建 厦门361005)



时间序列平稳性分类识别研究

管河山1，邹清明1，罗智超2

(1.南华大学 经济管理学院,湖南 衡阳421001；2.厦门大学 王亚南经济研究院，福建 厦门361005)

摘要：平稳性检验是时间序列回归分析的一个关键问题，已有的检验方法在处理海量时间序列数据时显得乏力，检验准确率有待提高。采用分类技术建立平稳性检验的新方法，可以有效地处理海量时间序列数据。首先计算时间序列自相关函数，构建一个充分非必要的判定准则；然后建立序列收敛的量化分析方法，研究收敛参数的最优取值，并提取平稳性特征向量；最后采用k-means聚类建立平稳性分类识别方法。采用一组模拟数据和股票数据进行分析，将ADF检验、PP检验、KPSS检验进行对比，实证结果表明新方法的准确率较高。

关键词：时间序列；平稳性；特征提取；分类

一、引 言

时间序列是一类典型的随机数据，基于随机变量的历史和现状推测其未来需要假设随机变量的历史和现状具有代表性或可延续性，样本时间序列展现了随机变量的历史和现状；随机变量基本形态维持不变也就是要求样本数据的本质特征仍能延续到未来，称这些统计量(均值、方差、协方差)的取值在未来仍能保持不变的样本时间序列具有平稳性[1]668-685。平稳性分析是时间序列回归分析中的共性问题，是经典回归分析赖以实施的基本假设；如果数据非平稳，则作为大样本下统计推断基础的“一致性”要求便被破坏，基于非平稳时间序列的预测也就失效。已有的平稳性检验方法可以归纳为主观分析方法和客观分析方法两大类。

主观分析方法包括时间路径图法、自相关函数、偏自相关函数、逆自相关函数等各种图形分析方法[2]，这类方法的主观判定性较强，可用于平稳性的粗略判定。以自相关函数分析为例，如果时间序列的自相关函数迅速收敛到0，则判定为平稳的，反之，则判定为非平稳的[1]668-685。然而，快速收敛到0是一种主观的判定方式，不但收敛参数选取困难(尚缺少一个“经验取值”)，而且“快速收敛”缺乏量化分析的依据，研究者通常是根据自相关函数收敛情况进行主观判断。在面临海量的时间序列数据时，如果采取这种方法进行逐个分析，其工作量是十分巨大的，而且这种主观判定的结果因人而异，难以得到一致的判定结果。因此，在平稳性检验的实践中，这类主观分析方法一般仅用于分析小批量的数据，且只能得到一个粗略的判定结果。

客观分析方法包括单位根检验(DF检验和ADF检验)、PP检验和KPSS检验 、LLC检验、Block Bookstrap检验、LR检验 和Perron检验等方法[3-11]。这些研究本质上是采用了统计分布的概念，因其完善的理论体系、较高的准确率以及客观的分析方式，此类方法得到了广泛的应用，成为现有平稳性检验实践中的主流方法。以DF检验方法为例，编译相关的宏变量(循环语句)，DF检验方法是可以处理海量的时间序列数据，这种借助统计分布和临界表的判定方式，其本质是给出统计意义上的某种近似结果；DF检验检验时需要对三种模型(均值项、趋势项的选取)进行综合判定分析，其分析的结果带有一定的经验性。因此，在平稳性检验的实践中，这类客观分析方法的准确率仍值得探究。刘田从样本长度的视角分析了单位根检验方法的准确性，发现单位根检验方法对模拟数据(基于AR模型的分析)的检验准确率有较大的差异[12]。本文实证也表明这些客观检验方法的准确性仍不够理想。

随着计算机技术的发展和数据采集能力的提升，金融、经济、医学、工程监控等领域的大量时间序列数据被收集，给时间序列研究提供了丰富的数据资源和广阔的应用空间。如何实现海量时间序列数据的平稳性分析是一件值得挑战的工作。本文主要是针对海量时间序列数据(时间长度大于500)的平稳性分析展开，在自相关函数分析的基础上，借助数据挖掘中的分类技术，构建平稳性检验的新方法。新方法不是对自相关函数的简单改良，而是通过引进分类技术(无监督的分类技术)为平稳性检验提供一个全新的检验方式，突破传统检验方法对统计分布和临界表的依赖，为海量时间序列数据的平稳性检验提供一种新的途径。

二、平稳性分类识别

平稳性检验方法的研究内容主要包括平稳性特征提取和检验方式两大部分。比如，主观分析方法中的自相关函数是提取自相关函数序列作为平稳性特征，并根据其收敛程度来进行判定(检验方式)；客观分析方法中的DF检验是构建DF检验统计量作为平稳性特征，并根据临界表来进行判定(检验方式)。因此，要解决时间序列平稳性检验问题，需要在平稳性特征提取和检验方式上进行深入研究，这正是本研究的出发点。

(一)平稳性特征提取

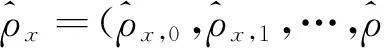
(1)

(2)

(3)

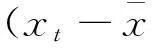
从表面上看，式(3)只是做了简单的反余弦转换，但实际上与后文的平稳性分类密切相关的。进行非线性转换主要原因有两方面:一方面，转换可以放大时间序列样本平稳性特征之间的差异，自相关函数的取值区间为[-1,1],经过反余弦函数转换，θm的取值区间为[0,π],这表明，通过反余弦函数的转换，可以放大平稳性的特征，而这一过程，也是一个等价的非线性转换过程，这有利于下一步的平稳性分类(类属性不同的样本之间的差异越明显，越有利于提高分类的准确率)；另一方面，转换后,序列θ收敛是自相关函数序列收敛的“充分非必要”条件，因此，判定准则将更加高效。具体证明如下：

|θm-θm-1|

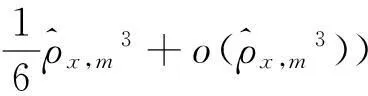
平稳性判定的新准则：对任意一个时间序列样本，计算其特征向量θ；如果向量元素θm快速收敛到0，则可以判定该样本是平稳的；反之，则判定该样本是非平稳的。

得到的新准则仍然是一种主观的判定方式，尚无法对海量数据进行处理，因此需要对判定准则展开量化分析和计算。下面从收敛参数的确定和特征空间的构建两个角度展开探讨。

2.序列收敛参数的确定。无论是传统的自相关函数分析方法，还是本文所提出的新准则，都是从分析序列收敛状态来判定时间序列的平稳性特征，此时参数m的确定仍缺少一个客观的方式。传统的自相关函数分析淡化了序列收敛的客观判定方式，这使得判断仍停留在主观判定的层面。

根据数列收敛的定义可知，如果向量元素θm快速收敛到0，则给定的阈值ε1和ε2(正数)，则存在一个正整数N，对所有的正整数m≥N，应满足式(4)。对平稳时间序列而言，元素θm将快速收敛到0，容易满足式(4)；对非平稳时间序列而言，将趋向于不满足式(4)。因此，可以对平稳性特征向量θ的收敛状况进行分析，探讨满足式(4)的样本所占百分比，进一步给出参数m的最优经验取值。

(4)

r=max (r1-r2)

(5)

采用大量的模拟数据进行实验(见表3和表4，采取时间长度为500、600、700、800、900、1 000六种模拟数据进行分析，每种时间长度取值、每个模型都模拟生成1 000个样本)。阈值ε1和ε2取值越大，则满足式(4)的样本所占百分比越多，但是考虑到“快速收敛”的原则，本文将对0.1、0.2和0.3三种取值进行分析，分别统计出满足式(4)的平稳样本比(r1)和非平稳样本比(r2)，并计算两者之差，如式(5)所示。求得差值最大时参数m的取值，计算结果如表1所示。

表1　参数m的经验取值

由表1可知，当给定的收敛阈值较大时，平稳时间序列将容易满足式(4)，此时r1取值较大，参数m取值较小；反之，r1值较小，参数m取值较大。从表1和式(4)分析，当收敛阈值取值为0.1时，对“收敛到0”特征的满足程度较高，而且平稳样本满足收敛的百分比为0.874 58，r取值为0.862 95，均大于85%；相反，当收敛阈值为0.2和0.3时，尽管平稳样本满足收敛的百分比超过95%，然而此时“收敛到0”特征的满足程度却较低。因此，一方面考虑到“收敛到0”的特征要求，另一方面使得两类样本满足收敛条件的样本百分比之差(r)最大化的原则，将收敛参数m的最优经验值定为m0=37。实验时，为了分析收敛参数m对实验结果的影响，对三种收敛阈值下的最优取值都进行了分析。在此，给出了某种收敛程度下的经验值分析，而采用经验值分析也是研究中常用的方式，这将为下一步的平稳性分类识别做好铺垫。

3.平稳性特征空间的构建。从上述分析可知,本文研究得到参数m的最优经验取值m0，此时，每个时间序列将可以提取相应的特征向量θ={θ1,θ2，…,θm0}。值得指出的是，采取自相关函数对平稳性进行主观判定时，侧重于“快速收敛到0”的探讨，淡化了“元素θm正负取值”的影响，因此将对特征向量θ取绝对值转换，具体如下：

(6)

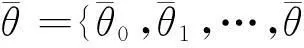
(二)时间序列平稳性分类识别

分类技术是数据挖掘研究中的一个重要内容，聚类分析是研究样品(或指标)分类问题的一种统计分析方法。分类研究主要包括三个部分：一是样本数据的特征提取，二是相似性度量函数的构建，三是分类的算法。这些研究中，前两者的研究居多，而分类算法大部分都是采用分类(有监督的分类)和聚类(无监督的分类)两大方式。本文采用聚类技术来探讨时间序列的平稳性检验，以求建立一种客观的平稳性判定方式。

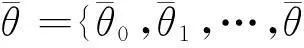
(三)平稳性分析方法的对比

本文提出的平稳性分类识别(SCI)方法，是在传统的自相关函数(ACF)分析方法基础上进行改进的，记为SCI-ACF方法。它通过等价转换提出了序列收敛判定的充分条件，并在此基础上研究收敛参数的最优取值，然后采用分类技术建立一种新的检验方式，使之能处理海量数据。两者之间的关系如表2所示。

表2　方法的对比分析表

三、 实验结果及分析

本文将采用模拟数据和股票数据进行分析。传统的自相关函数无法处理海量时间序列数据，ADF检验、KPSS检验和PP检验方法可以通过编译宏变量，实现对海量时间序列数据的平稳性判定，本文采用这三种方法进行对比实验。其他的检验方法大多是针对特定的数据类型展开分析的，在此不做过多分析。实验采用了SAS软件(SCI-ACF方法)和MATLAB软件(ADF检验、KPSS检验和PP检验)进行编程处理。

(一)仿真数据分析

1.仿真实验数据。生成6组非平稳时间序列数据和6组平稳时间序列数据进行实验分析[2,15]。在模型参数的选择上，尽量使得生成的时间序列样本难以区分，即难以判定时间序列的平稳性与非平稳性。具体模拟生成函数如表3、表4所示：

表3　模拟非平稳时间序列

表4　模拟平稳时间序列

其中，et为服从标准正态分布的伪随机函数。模拟数据的时间长度分别取500、600、700、800、900、1 000和1 500，每组模拟时间序列各生成1 000个时间序列样本，模拟共计生成8.4万个时间序列样本。

2.实验结果及分析。第一，采用ADF方法进行检验，统计检验准确率如表5所示(计算结果保留1位小数点)。从表5可看出，对7种时间长度的时间序列数据而言，ADF检验方法的准确率都在97%以上，但都低于98%，这一实验结果说明ADF方法长期以来成为平稳性检验主流方法的原因。另外，由表5可知，PP检验的准确率超过97%，检验准确率比较高，KPSS检验的准确率低于70%。综上所述，在三种传统的检验方法中，ADF检验呈现出较好的性能。

表5　检验准确率(单位：%)

第二，采用平稳性分类识别方法(SCI-ACF)进行分析，统计得到平稳性检验的准确率，如表5所示。从表5容易看出：对7种时间长度的时间序列数据而言，平稳性分类识别方法得到的准确率较高，明显高于ADF检验、PP检验和KPSS检验三种方法的准确率；当序列时间长度较大时(大于600时)，平稳性分类识别方法的准确率都超过了99%。进一步，考虑到最优参数m的选取是跟收敛阈值相关的，本文对其他两种收敛阈值所对应的最优收敛参数也进行了分析。分别统计出m0等于22、29和37时平稳性分类识别方法的准确率结果，记为C22、C29和C37，并与ADF检验方法的准确率进行对比，如图1。显然，三种收敛阈值所对应的最优参数m0，其分析的准确率都优于ADF检验方法，因此从仿真实验结果来看，平稳性分类识别的准确率较高。

图1　平稳性分类识别与ADF的对比分析图

第三，对模拟数据采用自相关函数方法进行分析，其主观分析的工作量十分巨大。假定绘制一个时间序列样本的自相关函数图形，并进行主观判定的时间为1分钟，则8.4万个样本分析，共需要1 400个小时，而且判定的结果将随个人差异而有所不同，因此本文不做详细探究。

(二)股票数据分析

1.股票数据。选择中国上证交易所股票的日价格数据(收盘价)和日收益率数据(考虑分红的日收益率)，数据来自CSMAR数据库，时间取样长度为1 000(2009/7/6-2013/9/5)，剔除数据不完整的股票样本，选取100个股票数据(价格数据和收益率数据分别100个)，共计200个样本用于分析。

2.实验结果及分析。基于仿真实验的准确率分析结果，选取准确率较高的两种方法(ADF检验和平稳性分类识别方法)进行分析，统计出两种方法的检验结果，如表6所示。由表6可以看出：ADF检验方法将91个价格数据判定为非平稳的，而将其中9个价格数据判定为平稳的，SCI-ACF方法将全部价格数据判定为非平稳的；ADF检验将100个收益率数据判定为平稳的，SCI-ACF方法也将100个收益率数据判定为平稳的。这表明，中国上证市场的股票日价格数据呈现出明显的非平稳性特征，而收益率数据呈现出明显的平稳性特征。

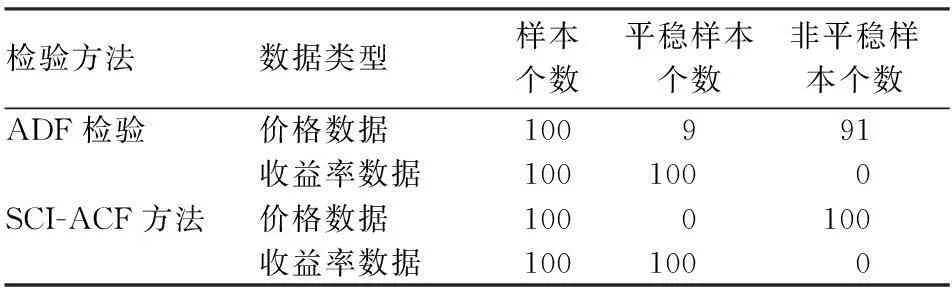
表6　股票数据的平稳性检验结果表

由于股票数据的平稳性特征事先是未知的，因此无法统计平稳性检验的准确率，在此有必要借助图形进行主观分析。绘制两种方法检验结果不一致的9个股票样本的图形，分别编号为S1～S9，如图2所示。不难发现，9个股票样本数据呈现出比较明显的递增(或递减)趋势，而非水平波动。因此，样本判定为非平稳是比较合理的，这表明SCI-ACF方法的检验结果是比较合理的。

图2　股票数据的走势图

四、结论

本文针对海量时间序列数据(且时间长度大于500)进行平稳性检验研究，提出了平稳性分类识别的新方法。主要研究工作有三个方面：第一，在提取自相关函数特征的基础上，采用反余弦函数转换放大时间序列样本平稳性特征之间的差异，得到平稳性判定的一个“充分非必要条件”，形成一个新的判定准则；第二，重点探究序列快速收敛到0的量化分析，给出了收敛参数m的确定方式，构建出平稳性特征空间，为量化分析和计算提供了依据；第三，采用k-means聚类算法建立平稳性模式分类和识别的方法。仿真实验表明新方法的准确率比ADF方法提高大约1～2个百分点(尽管ADF方法准确率已经比较理想)。本文提出的平稳性检验的新方法，拓展了时间序列数据挖掘技术在平稳性检验中的应用研究，也打破了传统ADF检验的“应用垄断”局面。

本研究不是对自相关函数的简单改良，而是引进数据挖掘中的分类技术，建立了平稳性分析的新模式，从平稳性特征提取和检验方式两个角度同时展开探究，所建立的新方法可以有效处理海量时间序列数据。这种新的检验方法突破了传统检验方法(ADF检验、PP检验和KPSS检验等)对统计分布和临界表的依赖。此外，本研究主要是针对时间长度较大的时间序列数据展开，而对时间长度较短的时间序列数据，由于其样本量较少，可能造成平稳性特征不明显，这使得平稳性分析方法的性能偏差。对时间长度较短的时间序列数据平稳性检验将是下一步研究的重点。

参考文献：

[1]J D Hamilton.Time Series Analysis[M].New Jersey:Princeton University Press,1994.

[2]C Jorge,C Nuno,P Daniel.A Periodogram-based Metric for Time Series Classification[J].Computational Statistics &Data Analysis,2006,50(10).

[3]D A Dickey.Estimation and Testing of Nonstationary Time Series[D].Ames:Iowa State University，1976.

[4]D A Dickey,W A Fuller.Distribution of the Estimators for Autoregressive Time Series with a Unit Root[J],Journal of American Statistical Association,1979,74(366).

[5]Westerlund Joakim.The Effect of Recursive Detrending on Panel Unit Root Tests[J].Journal of Econometrics,2015,185(2).

[6]邓露.最优滞后长度与ADF检验性质研究及其应用[J].统计与信息论坛,2010,25(9).

[7]周敏，蔺富明.小样本PP检验统计量的分布特征[J].西南大学学报，2015,37(5).

[8]冯蕾，聂巧平.结构突变对KPSS检验水平与检验功效的影响——基于有限样本情形的模拟及实证研究，统计研究，2009,26(9).

[9]Levin A，C F Lin,C S J Chu.Unit Root Tests in Panel Data :Asymptotic and Finite-sample Properties [J].Journal of Econometrics，2002,108(1).

[10]张华节，黎实.面板数据单位根似然比检验研究[J].统计研究，2015，32(4).

[11]莫扬，张捷.带结构突变的确定趋势的单位根检验方法[J].数量经济技术经济研究，2012(2).

[12]刘田.单位根检验中样本长度的选择[J].数理统计与管理，2013，32(4).

[13]R C morim， B Mirkin，Minkowski Metric.Feature Weighting and Anomalous Cluster Initializing in K-Means Clustering[J].Pattern Recognition，2012，45 (3).

[14]管河山,邹清明,邓灵斌.时间序列平稳性分析的自动机制研究[J].南华大学学报,2010,11(3).

(责任编辑：张爱婷)

收稿日期：2015-11-18；修复日期：2015-12-10

基金项目：教育部青年基金项目《海量金融时间序列数据平稳性检验方法研究》(13YJCZH044)

作者简介：管河山，男，湖南衡阳人，理学博士，副教授，研究方向：时间序列数据挖掘；

中图分类号：O211.61∶F830.91

文献标志码：A

文章编号：1007-3116(2016)04-0003-06

Study on Classification and Identification of Time Series Stationarity

GUAN He-shan1，ZOU Qing-ming1，LUO Zhi-chao2

(1.School of Economics and Management,University of South China,Hengyang 421001,China;2.Wang Yanan Institute for Studies in Economics,Xiamen University,Xiamen 361005,China)

Abstract:Stationarity test is a key problem of time series regression analysis,existing methods of stationarity test can hardly deal with the massive data,the test accuracy needs to be improved.Based on the analysis of classification,this paper would build a new method for stationarity test,which could effectively deal with massive time series data.Firstly,it calculates the autocorrelation function and then construct a fully and non-necessary criterion; secondly,establish a kind of quantitative analysis of sequence convergence,the optimal value of the sequence convergent parameter is given out，and then take out the characteristic of stationarity; finally,the k-means clustering algorithm is used to establish stationarity classification and recognition method.This paper makes empirical analysis with a set of simulated data and a group of stock data,which results show that our method's accuracy is not only higher than that of the ADF test，and than that of KPSS test and PP test.

Key words:time series; stationarity; feature extraction; classification

邹清明，男，湖南衡阳人，经济学博士，副教授，研究方向：多元统计；

罗智超，男，福建厦门人，高级工程师，研究方向：计量经济。

【统计理论与方法】