乘法需求的两阶段供应链优化问题

董　琦



乘法需求的两阶段供应链优化问题

董琦

北京邮电大学理学院

行业曲线

本文针对面临乘法随机需求的季节性商品供应链模型，提出使供应链利润最大化的零售商销售价、进货量和供应商生产能力的求解方法。在经济管理领域起到很大作用。

如付诸现实将产生宏观上促进销售行业供应链运行的经济效益。

本文中我们研究了季节性商品销售的两阶段供应链模型，此供应链为单一供应商和单一零售商，且零售商面对的随机乘法需求模型。在销售季到来之前的第一阶段，供应商根据历史数据和初步调查预测即将到来的市场需求，并由此决定对于此商品的预留生产能力，经过一段时间预备期后进入第二阶段，供应商和零售商更新市场需求，零售商决定进货量和售价。对于此供应链，我们做出集中决策下的分析，在考虑第二阶段时，为使整个供应链的预期收益最大化，求得最优的进货量和售价；然后考虑第一阶段，求得最优的预留生产能力。

本文中，我们研究了集中决策下的优化问题，此问题中，单一供应商和零售商面临季节性商品的市场需求，在销售季到来之前，供应商首先决定初始的预留生产能力，零售商的进货需求受到预留生产能力的影响，进货量超过预留生产能力的部分无法被满足。我们将销售季到来之前的时段分为两个阶段，第一阶段由供应商根据历史销售数据确定预留生产能力，进而在第二阶段由零售商确定进货量、售价并告知供应商，供应商收取生产费用并生产货物，运送至销售商，销售季到来。对于整个供应链，我们需要考虑如何协调供应商和零售商以使得总利润最大。

报童模型和供应链协调性的研究由来已久。报童模型是供应链研究的基础，在本文的模型中，零售商可以作为报童。报童问题的理论研究可以追溯到1888年，经济学家Edgeworth在研究银行现金流的过程中引入了报童模型的概念。1955年，Whitin首先提出了受价格影响的需求模型，对本文影响最大的是1999年由Petruzzi和Dada提出的加法和乘法形式的需求函数模型。在供应链问题的研究中，研究目标着重放在优化进货量和售价等参数上。对于季节性商品，决策者更倾向于以整个供应链的收益最大化为目标，因为此类型供应链若无法在当季正常运行会带来损失。2010年，Frank Chen等提出了两阶段供应链模型，应用了加法需求函数，对进货量、售价等决策变量进行了优化并给出协调合同。

本文中最大的创新点在于对需求函数的改良，我们研究了以乘法需求函数为基础的两阶段供应链模型，并将预留生产能力作为不计成本的决策变量。在第二部分，我们给出了模型的参数假设和说明；在第三部分，我们给出了集中决策下的最优化参数值；在第四部分，我们给出结论。

参数假设

m：供应商的预留生产能力；

D ：市场需求随机变量；

p ：零售商的单位销售价格；

q ：供应商向零售商提供的单位进货量；

c ：零售商在第二阶段决定的单位销售价格；

u ：未使用预留生产能力的单位回收价；

v ：未售出剩余商品的单位回收价；

π：短缺商品的单位惩罚损失。

关于模型我们做出以下几点说明：

1.需求函数的形式：

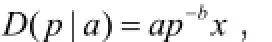
其中，b＞1；x是一个取非负值的随机变量，其取值区间为［L, H］，概率密度函数为f（x），概率分布函数和数学期望分别是F（x）和E（x）=µ；参数a在两个阶段中有不同意义：在第二阶段，我们认为a是一个正值常数，因为它可以由历史销售数据得到，特别是它对决策变量的优化并没有影响；然而在第一阶段，a被认为是一个取正值的随机变量，这是由于在考虑决策变量M的优化时，a是一个重要的未知变量，此时，我们设定a是一个取值在［l, h］上的连续随机变量，概率密度函数为g（⋅）。

2.b是一个常数，因为它可以由相同或者相似商品的历史销售数据得到，所以在第一阶段可以确定。

3.随机变量x 满足：

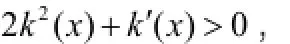
集中决策下的供应链

在这一部分，我们将研究集中决策下的供应链模型，分为两个阶段。我们首先考虑第二阶段，然后考虑第一阶段。在第二阶段，我们给定常数a，在此基础上确定最优的进货量和销售价；在第一阶段，我们把a作为随机变量，在此基础上给出最优的预留生产能力m。

第二阶段决策

在第二阶段，我们的目标是在给定预留生产能力M的情况下寻找最优的进货量和销售价，最优决策是通过分析整个供应链的利润函数得到，分为两种情况：第一种情况是预留生产能力无限制，可以满足进货量；另一种情况是预留生产能力不能满足进货量。根据之前的参数假设，在第二阶段，我们将a作为取正值的常数，用aˆ 表示，因此，需求函数为：

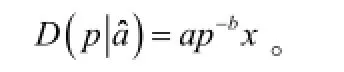
预留生产能力无限制的情况

在预留生产能力无限制时，q＜M，我们令Π1（p, q）表示此时整个供应链的利润函数；

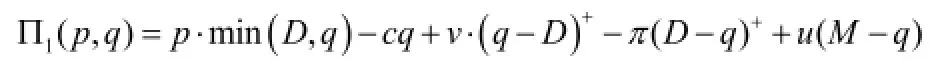
为了便于计算，我们定义安全存货因子：

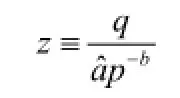
此时，在利润函数中我们用变量z 替换变量q ，同时规定，。那么，q＜M时对应的供应链利润Π的期望为：

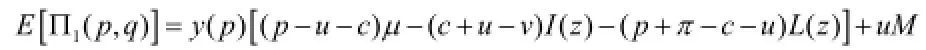
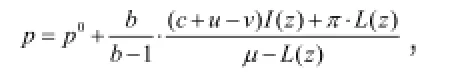
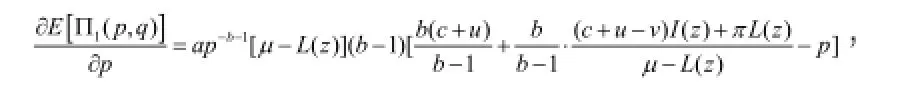
证毕。

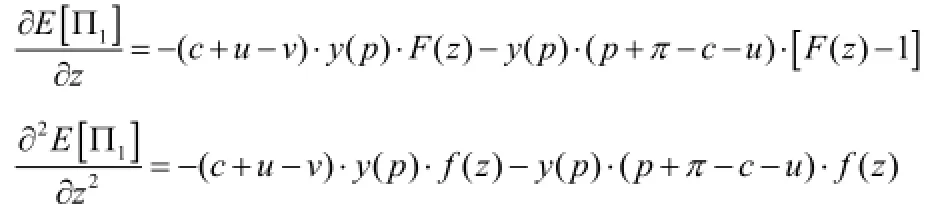
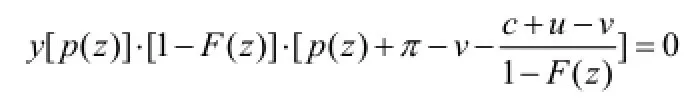
证明：根据引理1和引理2，我们有：

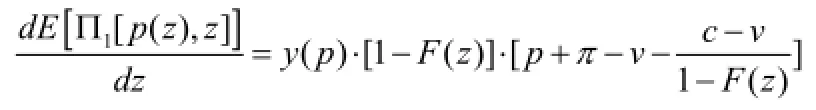
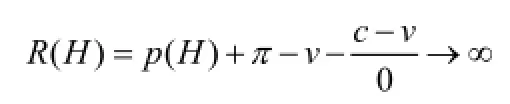
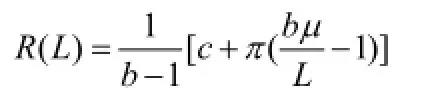
由于b＞1，µ＞L ，所以，R（L）＞0。

接下来我们考虑R（z）的函数性质：

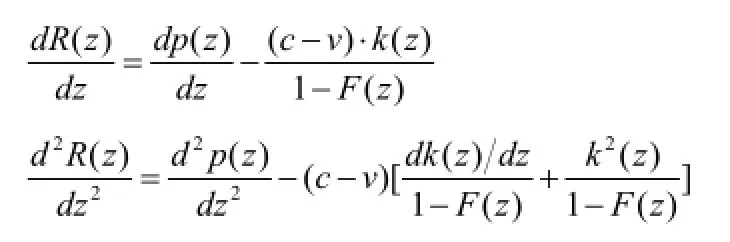
根据引理1，

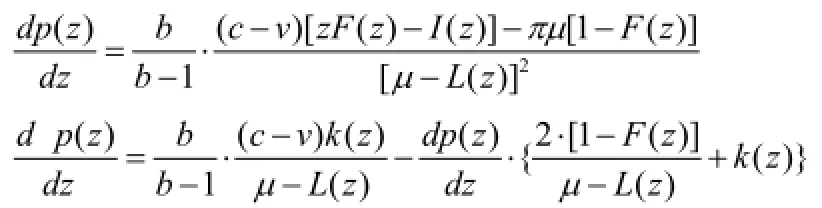
因此，

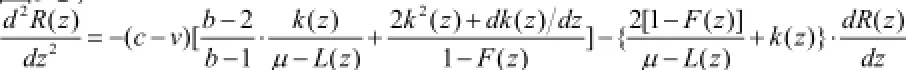
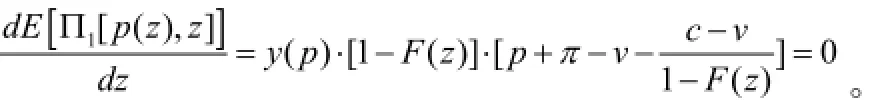
证毕。

预留生产能力有限制的情况

接下来我们考虑预留生产能力有限制的情况，即q≥M，我们令表示此时整个供应链的利润函数。由于进货量最多只可以达到预留生产能力的水平，因此此时实际上有q=M，利润函数期望实际上只是价格p的函数，即。则，

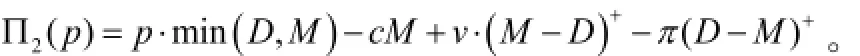
它对随机变量x的期望是：

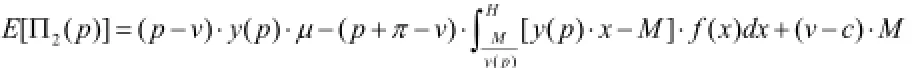
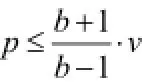
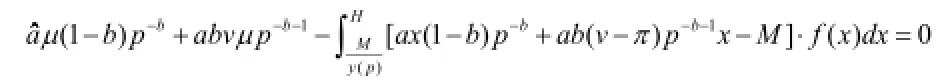
证明：根据E［Π2（p）］的表达式，我们可以得到：

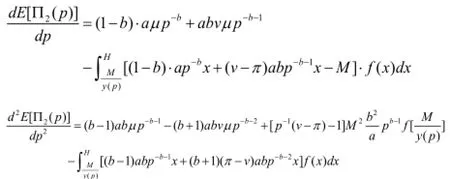
对上式进行分析，我们可以认为p＞1，而由于，所以上式第三项为负值；第四项显然也为负值。所以我们考虑前两项，若有，则可以得到，即是凹函数，具有惟一的最优值点p#，且满足。根据条件成立。

证毕。

第一阶段决策

接下来我们返回第一阶段的决策，即我们需要确定预留生产能力M的最优值。这里我们需要讨论作为随机变量的参数a 与M 的关系，进而得到M的最优值M*。首先我们考虑M的取值范围。令h*（a）=a［p（z*）］-b⋅z*，实际上，h*（a）就是第二阶段在无预留生产能力限制情况下的最优进货量。我们把它作为a的函数，显然，，所以h*（a）关于a单调递增。直观含义是当市场规模较大时，最优的进货量也应该较大。那么h*（a）的取值范围是［h*（l）,h*（h）］。我们分别用和表示生产能力无限制和生产能力有限制情况下的供应链最大预期收益。于是，整个供应链的预期收益函数是：

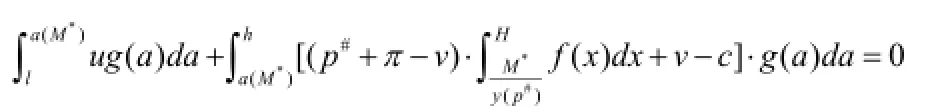
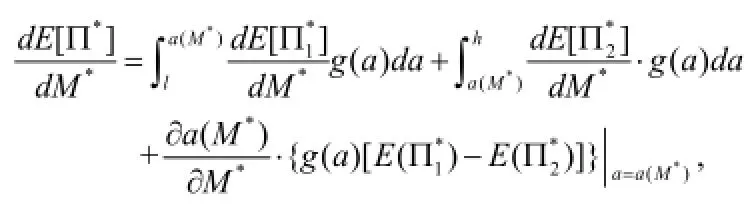
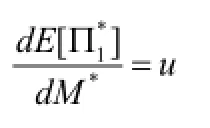
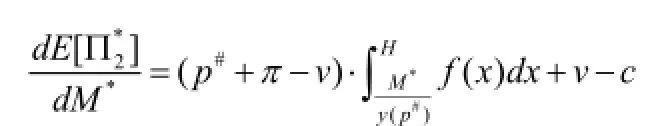
所以，

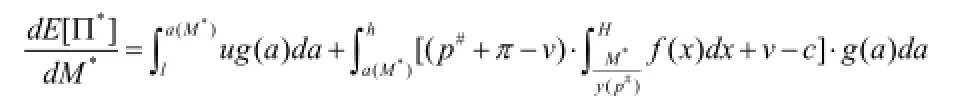
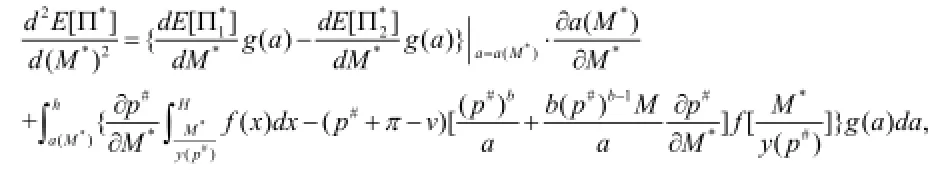
根据上述分析，当a=a（M*）时，我们有，

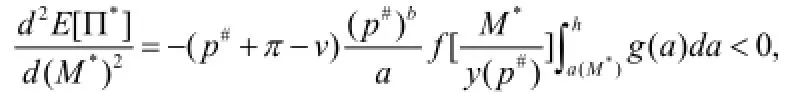
证毕。

说明：M*的取值有另外两种情况，分析如下：

在这种情况下，M*比最优进货量的最大值还要大，即预留生产能力无限制。此时，供应链收益的目标函数为：

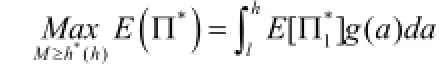
第二种情况：M*≤h*（l）。

在这种情况下，M*比最优进货量的最小值还要小，即预留生产能力有限制。此时，供应链收益的目标函数为：

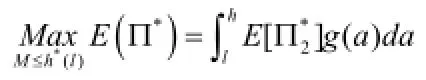
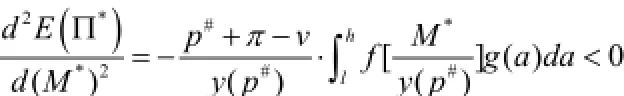
所以在供应链的第一阶段的最优预留生产能力惟一且在第二阶段的最优进货量是M*。

综上，我们可以根据定理1得到最优的z*，并因此确定a（M*）与M*的函数关系，那么对于给定的M*，我们可以通过定理2确定p#；进而由定理3求解出最优的预留生产能力M*。

结语

我们考虑了基于乘法需求模型的两阶段供应链优化问题，优化的目标变量是进货量、销售价和预留生产能力。我们考虑了两种情况：预留生产能力无限制和有限制。在两阶段的模型设计中，第一阶段为前期市场需求预测和确定预留生产能力，第二阶段为成熟市场需求预测和确定进货量、销售价。我们对此问题进行优化的顺序是先确定两种情况下第二阶段的最优进货量和销售价，然后返回第一阶段将两种情况综合考虑，确定最优的预留生产能力。

DOI：10.3969/j.issn.1001- 8972.2016.13.026