一种二维鲁棒随机权网络及其应用

陈甲英，曹飞龙

(中国计量大学 理学院，浙江 杭州 310018)



一种二维鲁棒随机权网络及其应用

陈甲英，曹飞龙

(中国计量大学 理学院，浙江 杭州 310018)

【摘要】二维随机权网络的主要特点是将矩阵数据直接作为输入，可以保留矩阵数据本身的结构信息，从而提高识别率.然而，二维随机权网络在处理含有离群值的人脸图像识别问题时效果往往不佳.为了解决该问题，提出一种新的人脸识别方法——二维鲁棒随机权网络，并用期望最大化算法来求解网络参数.实验结果显示，该方法能够较好地处理含有离群值的人脸识别问题.

【关键词】人工神经网络；二维随机权网络；人脸识别；期望最大化算法

人脸识别技术是模式识别、图像处理、机器视觉、神经网络等领域的研究热点之一，已广泛应用于身份识别、证件验证、银行和海关的监控、门卫系统、视频会议、机器智能化以及医学等方面.传统的人脸识别一般分为四个步骤：人脸检测，图像预处理，特征提取和构造分类器分类.其中特征提取和分类是人脸识别研究的关键.

人脸识别按照人脸样本的来源可分为两类：基于静态人脸图像的识别和基于包含人脸动态信息的识别.本文所提及的方法都是基于静态人脸图像的识别.现有的人脸识别方法主要有：基于几何特征的人脸识别方法[1-2]，基于统计特征的人脸识别方法[3-10]，基于模型的人脸识别方法[11-14]和基于神经网络的识别方法.Carpenter首次将神经网络应用于模式识别[15]，Cottrell等在文献[16]中使用BP神经网络进行人脸识别.随后，LIN和KUNG等人[17]结合神经网络和统计学方法提出了概率决策神经网络(probabilistic decision-based neural network, PDBNN)模型，并将该模型应用于人脸识别，文献[18]、[19]提出了基于径向基神经网络(radial basis function neural network, RBF)的识别方法，文献[20]和[21]提出了基于支持向量机(support vector machine, SVM)的识别方法.但是，这些均是处理输入向量形式的识别方法，2014年LU等人[22]考虑了识别图像本身的结构信息，将向量输入的一维随机权网络推广到了二维情形，提出了一种二维随机权网络(two dimensional neural networks with random weights, 2DNNRW)并将它成功地应用到了人脸识别中.2015年CAO等人[23]提出了一种概率鲁棒随机权模型(probabilistic neural networks with random weights, PRNNRW)能够很好地处理含有噪声的数据.我们知道，在实际应用中，人脸图像往往含有离群值，在考虑结构信息的同时又能够较好地处理含有离群值的人脸识别问题无疑是值得研究的问题，本文的目的就在于此.

本文结构如下：第一节简要介绍一维随机权网络；第二节主要介绍二维鲁棒随机权网络及其外权的求解方法；第三节是实验部分，用四个不同的人脸数据库中的数据做实验，实验结果说明本文所提出的方法是有效的；第四节给出本文的结论.

1随机权网络

一般地，一个单隐层前向神经网络模型可以表示如下：

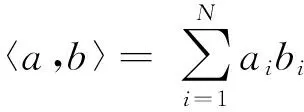
在监督学习理论中，神经网络的隐层参数和输出权需要根据训练样本训练得到.一个常用的参数学习方法为BP算法(errorback-propagation, BP)，它通过梯度下降的方法来调节权值和阈值的.然而BP算法收敛慢而且往往得到的是局部极小解.文献[24]首次提出一种单隐层前向神经网络的快速学习算法，即随机权网络(neural networks with random weights, NNRW).之后，PAO等人[25-27]提出了类似的方法：随机泛函连接网络，并且证明了它有万能逼近能力.最近，在文献[28-30]中又提出一些先进的随机学习算法.事实上，NNRW的主要思想是：给定一个样本集，输入权值和阈值是服从某种随机分布的随机变量，输出权可以利用最小均方误差算法来计算.

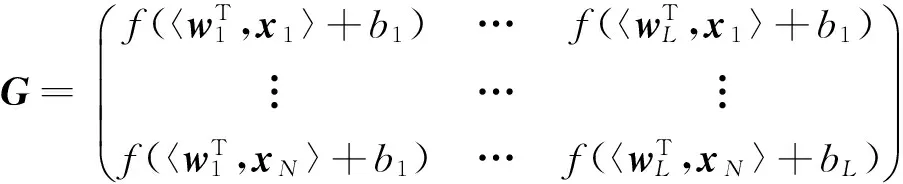
在处理人脸识别问题时，NNRW虽然耗时少，但是要先将样本转换为列向量，这样的处理将破坏样本相邻像素之间的相关性，从而影响识别效果.同时，对于含有离群值的数据，NNRW处理效果并不理想.针对这些问题，本文提出一种二维鲁棒随机权网络(Two Dimension Robust Neural Networks with Random Weights, 2DRNNRW).

2二维鲁棒随机权网络

利用NNRW进行人脸识别时，需要先将人脸图像或者图像特征转换为列向量，这将破坏原始图像或图像特征元素之间的相关性，从而影响分类结果.同时，2DNNRW[22]在处理含有离群值的人脸识别问题时效果并不理想.为了得到一个对离群值具有鲁棒性且识别效果较好的模型，本文提出了一种二维鲁棒随机权网络(2DRNNRW)，用期望最大化算法(Expectation Maximization Algorithm，EM)[31]来求解网络外权，并将它成功地应用到人脸识别问题.

根据文献[22],2DNNRW可以表示为

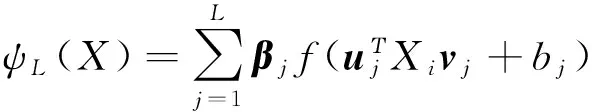
(5)

给定一组人脸图像训练样本集：

{(Xi,yi)|Xi∈Rm×n,yi∈Rl,i=1,2,…N},

N是训练样本数，l是类别数.根据(5)式我们可以得到如下的线性方程：

Gβ=Y.

(6)

其中β=[β1,β2,…,βL]Τ，Y=[y1,y2,…,yN]T，

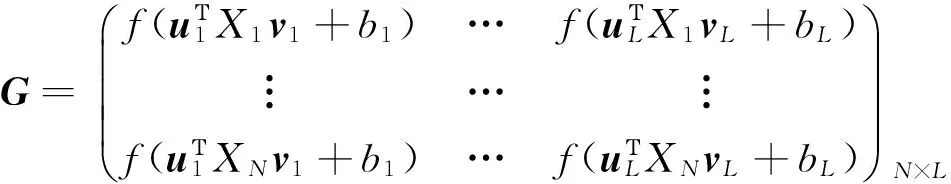
(7)

同样地，2DNNRW的输出权β可以通过求解如下的均方误差最小优化问题：

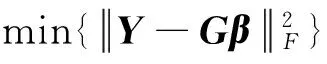
(8)

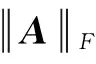
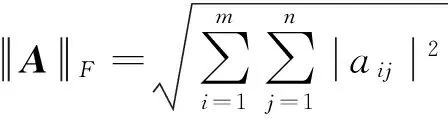
且A∈Rm×n，aij是A中第i行j列的元素.

根据文献[32]，输出权的范数和训练误差越小，网络的泛化性能越好.基于此，文献[29]提出了一种正则化模型

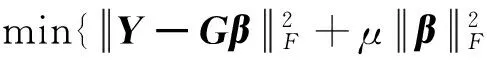
(9)

其中μ>0是一个常数，用来平衡训练误差项和惩罚项.由于F范数惩罚项的作用，模型(9)有更好的泛化性和稳定性.然而，在有离群值存在的情况下，模型(8)和(9)中误差的F范数损失函数缺乏鲁棒性.

事实上，样本数据通常含有离群值和噪声，因此，考虑到离群值和噪声的影响，(6)式变为

Y=Gβ+e.

(10)

其中G如(7)式所示，Y=[y1,y2,…,yN]T是类别标签矩阵，e是误差矩阵.

(11)

其中τ>0是正则化参数.

由于求解模型(11)是一个NP-Hard问题[33]，文献[34]指出，最小化l1范数可以得到稀疏解.因此，用l1范数来代替(11)式中的l0范数，从而得到了一个新的鲁棒随机权模型：

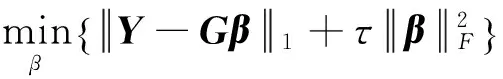
(12)

假设输出权β满足Gaussian分布，误差e满足Laplace分布，根据文献[23]可以将求解模型(12)的问题等价转化为一个最大后验概率估计问题,即

Y=Gβ+e

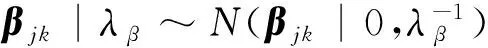
(13)

eik|λ～L(eik|0,λ),

i=1,2…N,j=1,2…L,k=1,2…L.

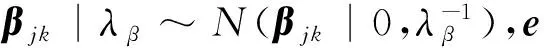
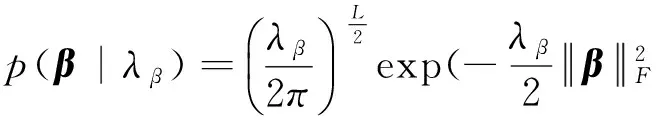
(14)

关于e的Laplace概率密度函数为

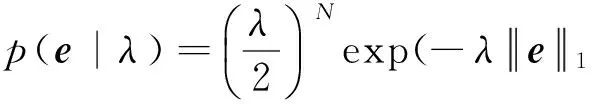
(15)

为了求解模型(13)，下面给出Laplace分布的一条性质[35]：

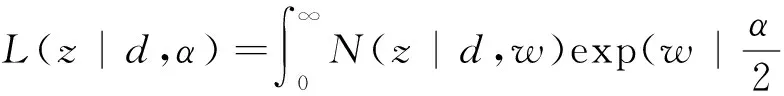
(16)

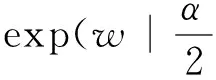
为了便于求解，引入一个与目标标签矩阵Y相关，并且服从指数先验分布的潜在变量W∈RN×l，根据Laplace分布的性质[35]，每个eik的Laplace分布可以表示为下面的形式：

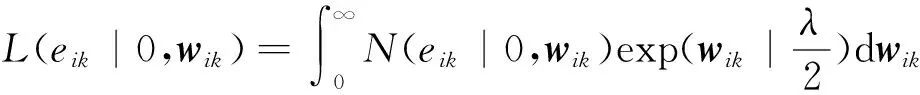
(17)

i=1,2,…N,k=1,2…L.

因此，模型(13)可以等价转化为求解如下的概率：

(18)

采用EM算法[31]求解模型(18).EM算法通过E-step和M-step的交替迭代来求解关于模型参数的最大后验概率.通常模型(18)与潜在变量W是独立的.将待估计参数第k次的估计值表示为βc.

在E-step计算所有数据关于潜在变量W的对数后验概率的期望：

Q(β,βc)=EW(log(p(β|Y,W)|Y,βc)).

(19)

根据贝叶斯准则，关于潜在变量W对数后验概率可以表示为

logp(β|Y,W)=

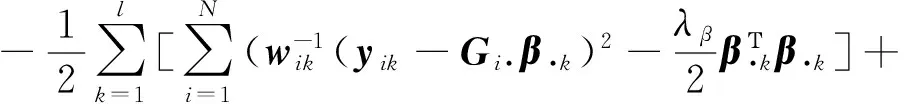
(20)

其中Gi表示输入权的第i行.

根据文献[36]中的命题18，可以得到

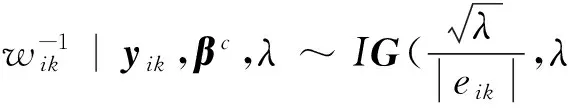
(21)

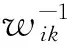
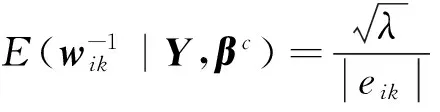
(22)

接下来，进行M-step求解β，即最大化关于β的模型(19)，对β求偏导数，并且令偏导数为0，求得β的形式解如下：

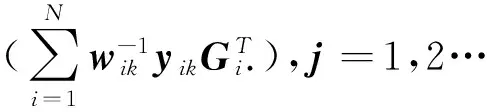
(23)

总结具体的算法如下.

鲁棒二维随机权算法

输入：样本集，

{(Xi,yi)|Xi∈Rm×n,yi∈Rl,i=1,2,…N},

隐层节点数L，激活函数f，正则化参数λ>0，λβ>0，终止误差ε，最大迭代次数max_iter.

步骤3随机初始化输出权β0；

步骤4用EM算法求解外权βc：

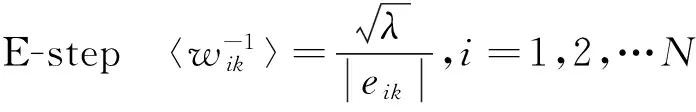
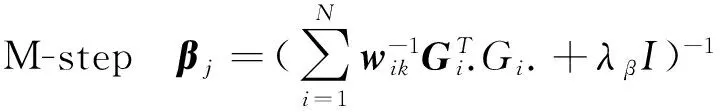
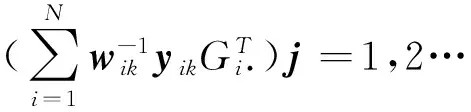
输出：β.

3实验结果及分析

本文所有实验都是在MATLAB7.11.0环境下进行，计算机配置为Intel(R)Core(TM)i3-4150@3.50GHz，内存为4.00GB.利用四个人脸数据库的数据做实验来验证本文所提出方法的有效性.表1给出了数据库相关信息，图1给出了数据集的部分样本.本文中所有实验结果数据都是实验运行30次结果的平均值.

本文参数设置为λ=0.01，λβ=0.1，

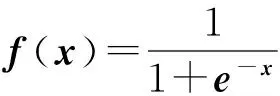
表1　试验中用到的数据集

本文用2DNNRW、PRNNRW和本文提出的2DRNNRW分别对表1给出的数据库中的数据进行分类，其分类精度显示在表2中.可以发现，对于不含离群值的数据集，2DNNRW和2DRNNRW的分类精度高于PRNNRW，这说明在人脸识别中，以矩阵作为输入的分类算法更具优势.

将表1中所列的人脸数据库中的数据人为地加入10%的离群值，然后分别用2DNNRW、PRNNRW和本文提出的2DRNNRW对加入离群值的人脸数据分类，实验结果记录在表3中.从表3可以发现两种鲁棒方法PRNNRW和2DRNNRW的识别精度均比2DNNRW高很多，因此，PRNNRW和2DRNNRW对于含有离群值的数据分类效果显著.但是，由于PRNNRW和2DRNNRW是通过迭代求解的，与2DNNRW相比，它们比较耗时.从表3、表4中实验结果可以发现较之PRNNRW，2DRNNRW耗时少且精度高.因此，在处理含有离群值的人脸识别问题时，2DRNNRW具有明显优势.

表2在不含离群值的数据集上平均识别率的对比试验

Table 2Comparison experiment of average recognition rate without outliers

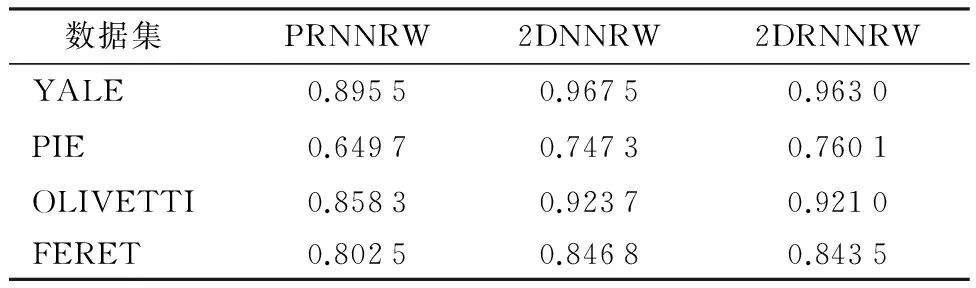
数据集PRNNRW2DNNRW2DRNNRWYALE0.89550.96750.9630PIE0.64970.74730.7601OLIVETTI0.85830.92370.9210FERET0.80250.84680.8435

数据集样本示例YALEPIEOLIVETTIFERET

图1数据库样本示例

Figure 1Examples of face dataset

在YALE和OLIVETTI数据库上，选取隐层节点数分别为200、400、600、800、1 000、1 200和1 400，分别用PRNNRW、2DNNRW和2DRNNRW对数据库中的人脸进行分类实验. 从图2、图3和表 5、表6可以发现随着节点数的增大，三个模型都趋于稳定.但是，本文提出的方法2DRNNRW的识别精度明显大于其他两种方法.

表3在含有离群值的数据集上平均识别率的对比试验

Table 3Comparison experiment of average recognition rate in the dataset with outliers

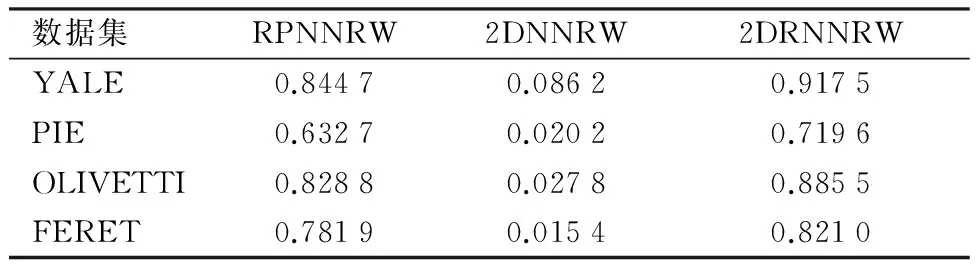
数据集RPNNRW2DNNRW2DRNNRWYALE0.84470.08620.9175PIE0.63270.02020.7196OLIVETTI0.82880.02780.8855FERET0.78190.01540.8210

表4在含有离群值的数据集上的平均测试时间

Table 4Comparison experiment of average testing time in the dataset with outliers

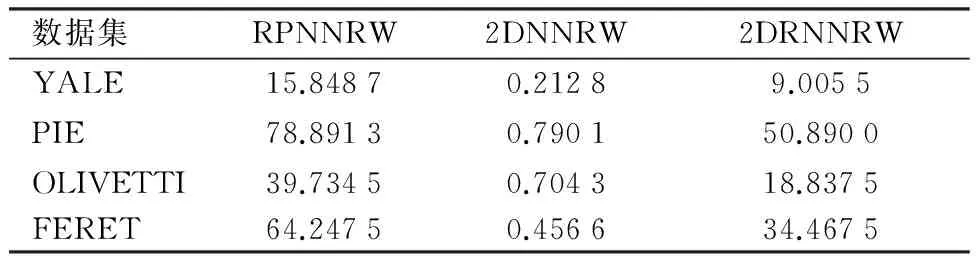
数据集RPNNRW2DNNRW2DRNNRWYALE15.84870.21289.0055PIE78.89130.790150.8900OLIVETTI39.73450.704318.8375FERET64.24750.456634.4675

4结语

由于传统的人脸识别分类器是以向量数据作为输入的，首先需要将人脸图像或矩阵形式的特征转化为向量形式，这样不可避免地破坏了人脸图像或者矩阵特征各元素之间的相关性，从而影响了分类效果.近年来，尽管出现了一些二维分类器，但是对于含有离群值的人脸图像识别问题效果并不好.针对以上问题，本文提出了一种二维鲁棒随机权网络.用左投影向量和右投影向量代替了单隐层前馈神经网络的高维输入权值，从而保留了矩阵输入的结构信息；同时，在求解外权时，采用一种l1惩罚函数和F范正则项的混合正则化模型.在模型参数和离群值满足某些分布的假设的前提下，用EM算法求解该模型.实验结果显示，本文提出的方法能够很好的处理含有离群值的人脸识别问题.

图2　PRNNRW、2DNNRW和2DPRNNRW在YALE数据库上不同的隐层节点下的识别率Figure 2　Recognition rate comparison of PRNNRW,2DNNRW and 2DRNNRW under differentnumber of hidden nodes on YALE datasets.

Table 5Comparison experiment of average recognition rate under different number of hidden nodes on the YALE dataset with outliers

算法200400600800100012001400PRNNRW0.71180.81340.83900.84350.86100.85160.86102DNNRW0.10450.07480.08090.07520.09110.08050.08292DRNNRW0.80280.88090.90240.91590.92850.92800.9191

表6在含有离群值的OLIVETTI数据库上不同隐层节点的平均识别率

Table 6Comparison experiment of average recognition rate under different number of hidden nodes on the OLIVETTI dataset with outliers

算法200400600800100012001400PRNNRW0.17570.53980.70270.79550.83500.86070.86822DNNRW0.03070.03930.02670.02570.02700.02580.02592DRNNRW0.25920.74170.84680.87730.89400.89900.9075

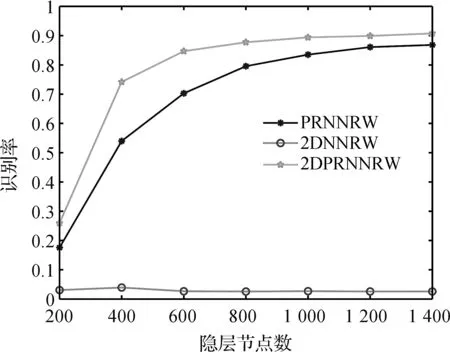
图3　PRNNRW、2DNNRW和2DPRNNRW在OLIVETTI数据库上不同的隐层节点数下的识别率Figure 3　Recognition rate comparison of PRNNRW, 2DNNRW and 2DRNNRW under different number of hidden nodes on OLIVETTI datasets.

【参考文献】

[1]LAM K M, YAN Hong. Locating and extracting the eye in human face images [J]. Pattern Recognition,1996,29(5):771-779.

[2]DENG J Y, LAI Feipei. Region-based template deformation and masking for eye-feature extraction and description [J]. Pattern Recognition,1997,30(3):403-419.

[3]TURK M, PENTLAND A P. Eigenfaces for recognition [J]. Journal of Cognitive Neuroscience,1991,3(1):71-86.

[4]SHERMINA J. Illumination invariant face recognition using discrete cosine transform and principal component analysis[C]// 2011 International Conference on Emerging Trends in Electrical and Computer Technology (ICETECT). Tamil Nadu: IEEE,2011:826-830.

[5]LU Jiwen, TAN Yappen, WANG Gang. Discriminative multi-manifold analysis for face recognition from a single training sample per person[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(1):39-51.

[6]ONKARE R P, CHAVAN M S, PRASAD S R. Efficient Principal Component Analysis for Recognition of Human Facial Expressions [J]. International Journal of Advance Research in Computer Science and Management Studies,2015,3(2):53-60.

[7]LU Guifu, ZOU Jian, WANG Yong. Incremental complete LDA for face recognition [J]. Pattern Recognition,2012,45(7):2510-2521.

[8]ZHOU Changjun, WANG Lan, ZHANG Qiang, et al. Face recognition based on PCA image reconstruction and LDA [J]. Optik-International Journal for Light and Electron Optics,2013,124(22):5599-5603.

[9]OH S K, YOO S H, PEDRYCZ W. Design of face recognition algorithm using PCA-LDA combined for hybrid data pre-processing and polynomial-based RBF neural networks: Design and its application [J]. Expert Systems with Applications,2013,40(5):1451-1466.

[10]BANSAL A, MEHTA K, ARORA S. Face recognition using PCA and LDA algorithm[C]// 2012 Second International Conference on Advanced Computing & Communication Technologies (ACCT). Rohtak, Haryana: IEEE,2012:251-254.

[11]SHARIF M, SHAH J H, MOHSIN S, et al. Sub-holistic hidden markov model for face recognition [J]. Research Journal of Recent Sciences,2013,2(5):10-14.

[12]CHUK T, NG A C W, COVIELLO E, et al. Understanding eye movements in face recognition with hidden Markov model[C]// Proceedings of the 35th Annual Conference of the Cognitive Science Society. Berlin: Cognitive Science Society,2013:328-333.

[13]MILBORROW S, NICOLLS F. Locating Facial Features with an Extended Active Shape Model[M]. Berlin Heidelberg: Springer,2008:504-513.

[14]COOTES T F, EDWARDS G J, TAYLOR C J. Active appearance models [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence,2001(6):681-685.

[15]CARPENTER G A. Neural network models for pattern recognition and associative memory [J]. Neural Networks,1989,2(4):243-257.

[16]FLEMING M K, COTTRELL G W. Categorization of faces using unsupervised feature extraction [C]// 1990 IJCNN International Joint Conference on Neural Networks. Maui: IEEE,1990:65-70.

[17]LIN Shanghung, KUNG Sunyuan, LIN Longji. Face recognition/detection by probabilistic decision-based neural network [J]. IEEE Transactions on Neural Networks,1997,8(1):114-132.

[18]JOOER M, CHEN Weilong, WU Shiqian. High-speed face recognition based on discrete cosine transform and RBF neural networks [J]. IEEE Transactions on Neural Networks,2005,16(3):679-691.

[19]MIGNON A, JURIE F. Reconstructing faces from their signatures using RBF regression [C]// 2013 Conference on British Machine Vision. Bristol, United Kingdom: [s.n.],2013:1-12.

[20]OSUNA E, FREUND R, GIROSI F. Training support vector machines: an application to face detection [C]// In 1997 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Juan: IEEE,1997:130-136.

[21]WEI Jin, ZHANG Jianqi, ZHANG Xiang. Face recognition method based on support vector machine and particle swarm optimization [J]. Expert Systems with Applications,2011, 38(4):4390-4393.

[22]LU Jin, ZHAO Jianwei, CAO Feilong. Extended feed forward neural networks with random weights for face recognition [J]. Neurocomputing,2014,136:96-102.

[23]CAO Feilong, YE Hailiang, WANG Dianhui. A probabilistic learning algorithm for robust modeling using neural networks with random weights [J]. Information Sciences,2015,313:62-78.

[24]SCHMIDT W F, KRAAIJVELD M, DUIN R P W. Feedforward neural networks with random weights [C]// 11th IAPR International Conference on Pattern Recognition Methodology and Systems. Hague: IEEE,1992:1-4.

[25]PAO Y H, TAKEFUJI Y. Functional-link net computing: theory, system architecture, and functionalities [J]. IEEE Computer Journal,1992,25(5):76-79.

[26]PAO Y H, PARK G H, SOBAJIC D J. Learning and generalization characteristics of the random vector functional-link net [J]. Neurocomputing,1994,6(2):163-180.

[27]IGELNIK B, PAO Y H. Stochastic choice of basis functions in adaptive function approximation and the functional-link net [J]. IEEE Transactions on Neural Networks,1995,6(6):1320-1329.

[28]ALHAMDOOSH M, WANG Dianhui. Fast de-correlated neural network ensembles with random weights [J]. Information Sciences,2014,264:104-117.

[29]CAO Feilong, TAN Yuanpeng, CAI Miaomiao. Sparse algorithms of random weight networks and applications [J]. Expert Systems with Applications,2014,41(5):2457-2462.

[30]SCARDAPANE S, WANG Dianhui, PANELLA M, et al. Distributed learning for random vector functional-link networks [J]. Information Sciences,2015,301:271-284.

[31]DEMPSTER A P, LAIRD N M, RUBIN D B. Maximum likelihood from incomplete data via the EM algorithm [J]. Journal of the Royal Statistical Society, Series B (Methodological),1977,39(1):1-38.

[32]BARTLETT P L. The sample complexity of pattern classification with neural networks: the size of the weights is more important than the size of the network [J]. IEEE Transactions on Information Theory,1998,44(2):525-536.

[33]NATARAJAN B K. Sparse approximate solutions to linear systems [J]. SIAM Journal on Computing,1995,24(2):227-234.

[34]DONOHO D L. For most large underdetermined systems of linear equations the minimal l1-norm solution is also the sparsest solution [J]. Communications on Pure and Applied Mathematics,2006,59(6):797-829.

[35]LANGE K, SINSHEIMER J S. Normal/independent distributions and their applications in robust regression [J]. Journal of Computational and Graphical Statistics,1993,2(2):175-198.

[36]ZHANG Zhihua, WANG Shusen, LIU Dehua, et al. EP-GIG priors and applications in Bayesian sparse learning [J]. The Journal of Machine Learning Research, 2012,13(1):2031-2061.

【文章编号】1004-1540(2016)02-0239-08

DOI:10.3969/j.issn.1004-1540.2016.02.020

【收稿日期】2015-12-14《中国计量学院学报》网址：zgjl.cbpt.cnki.net

【基金项目】国家自然科学基金资助项目(No.61272023,91330118).

【作者简介】陈甲英(1989-)，女，甘肃省金昌人，硕士研究生，主要研究方向为矩形恢复、神经网络.E-mail:1041074676@qq.com 通信联系人：曹飞龙，男，教授.E-mail: flcao@cjlu.edu.cn

【中图分类号】TP183

【文献标志码】A

A novel two dimension robust neural networks with random weights and its applications

CHEN Jiaying, CAO Feilong

(College of Sciences, China Jiliang University, Hangzhou 310018, China)

Abstract:The major advantage of two dimensional neural networks with random weights (2DNNRW) is to use matrix data as the input directly to reserve the structural information of the matrix data itself. Hence, compared with the neural networks with random weights (NNRW), the recognition rate is improved. However, the existing 2DNNRW is not good at the face recognition with outliers. Now, we proposed a two dimension robust neural networks with random weights (2DRNNRW). The expectation-maximization algorithm (EM) was used to calculate the parameters of the networks. Experiments on different face databases demonstrate that the proposed algorithm is effective to deal with the problem of face recognition with outliers.

Key words:artificial neural networks; neural networks with random weights; face recognition; expectation-maximization algorithm