用于滚动轴承转频估计的EMD软阈值降噪算法

程卫东,赵德尊

(北京交通大学 机械与电子控制工程学院,北京 100044)



用于滚动轴承转频估计的EMD软阈值降噪算法

程卫东,赵德尊

(北京交通大学 机械与电子控制工程学院,北京 100044)

摘要:针对经验模式分解(EMD)互相关系数-峭度准则降噪方法与小波阈值降噪方法的不足,提出EMD与小波软阈值降噪相结合的降噪方法.该方法主要包括以下4部分：1)对原始信号进行EMD分解得到固有模态函数(IMF)的集合；2)计算各个IMF与原始信号的互相关系数以及各IMF的峭度值；3)利用互相关系数-峭度准则选择需要降噪的IMF以及需要剔除的IMF；4)对选定的IMF进行阈值降噪后与剩余的IMF相加重构信号.利用仿真和实测的故障轴承信号对所提出算法以及EMD互相关系数-峭度准则降噪方法进行对比验证.结果表明：采用EMD软阈值降噪方法比采用EMD互相关系数-峭度准则降噪方法对信号进行预处理,更能确保轴承振动信号的完整性,突出信号的故障特征,降低瞬时转频估计的误差.

关键词：经验模式分解(EMD);软阈值降噪；滚动轴承；信号预处理；瞬时转频(IRF)估计

为了克服相关硬件设备安装空间及安装成本对传统阶比分析技术的限制[1-3],阶比分析技术框架下不依靠转速计直接根据时域振动信号对瞬时转频进行估计的研究引起了广泛关注[4-5].Boashash等[6-7]详细讨论了瞬时频率这一概念并从时频分布的角度对其进行估计.郭瑜等[8]利用峰值搜索算法对电动机变转速振动信号时频图中的瞬时频率进行提取以估计其瞬时转频.赵晓平等[9]则提出了短时傅里叶与Viterbi拟合算法相结合的方法对与卧旋离心机瞬时转频相关的瞬时频率进行提取.然而,对于变转速滚动轴承振动信号，基于时频谱的瞬时转频估计方法无能为力.为此，Wang等[10]提出了基于瞬时故障特征频率(instantaneous fault characteristic frequency, IFCF)的滚动轴承瞬时转频(instantaneous rotational frequency, IRF)估计方法.该方法对于滚动轴承瞬时转频的提取有较好的效果.但实际工况中滚动轴承低转速运行[11-12]和早期故障[13-15]普遍存在.此时,故障冲击信息易被背景噪音覆盖,较低信号的信噪比.基于IFCF的IRF估计方法由于受到噪声干扰,估计的瞬时转频将会产生较大的误差,其中根据实验数据可知低信噪比情况下误差可达到25%,甚至更多,这将严重影响后续滚动轴承的故障诊断.因此,需要对原始信号进行降噪预处理以降低滚动轴承瞬时转频估计的误差.

随着经验模态分解(emprical mode decomposition, EMD)方法的提出,近年来很多学者尝试将该技术及其扩展算法用于振动信号的降噪预处理.苏文胜等[16]提出了基于互相关系数-峭度准则的EMD 降噪方法并运用于滚动轴承的早期故障诊断.彭畅等[17]则提出了EEMD(ensemble EMD)度量因子(相似性度量和基于距离的度量因子)的降噪方法.唐贵基等[18]将互相关系数-峭度准则与EEMD相结合选择最优固有模态函数(intrinsic mode function, IMF)分量重构信号以降低滚动轴承振动信号中的噪声成分.该类算法的主要思想是根据一定准则筛选出含有有用成分的IMF分量对信号进行重构,其他分量则被认为是伪分量或者噪声予以剔除.然而,在低信噪比条件下,比如：早期故障或者低转速运行,滚动轴承振动信号中含有强烈的背景噪音,往往噪声起主导作用的IMF分量中也含有故障冲击成分.因此，单纯根据相关准则选择某几个IMF分量重构信号容易丢失原有信号的有用信息,对后续的瞬时转频估计以及阶比分析的结果造成影响.小波变换[19-20]由于基函数固定、多分辨率恒定等因素的限制缺乏自适应性.对于滚动轴承变转速振动信号而言,小波阈值去噪过程中最优分解层次以及小波基函数不易确定,降噪步骤较为繁琐.

为此,本文在上述方法的基础上提出EMD互相关系数-峭度准则降噪与小波软阈值降噪相结合的方法对滚动轴承变转速信号进行预处理,然后根据基于瞬时故障特征频率的滚动轴承瞬时转频估计方法对转频进行估计.EMD软阈值降噪方法通过对原始信号进行EMD分解得到本征模态函数；设定互相关系数和谱峭度值阈值,根据互相关系数-峭度准则剔除伪分量、选出需要进行降噪的IMF分量,对选定的IMF分量进行软阈值降噪；最后将降噪后的IMF分量与剩余的IMF分量相加重构信号.

1EMD降噪算法在滚动轴承瞬时转频估计中的问题

EMD是由Huang等[21]提出的一种自适应的信号分解方法,基于信号的局部特征,无须选择基函数就可将原始信号分解为许多窄带分量,即IMF.每个IMF分量满足以下2个条件：1)在整个数据段内,极值点的个数和过零点的个数必须相等或最多相差一个；2)在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零.IMF分量按频率从高到低依次分布,每个IMF分量中的频率成分随信号本身变化而变化.不同于传统的滤波器,EMD适用于非线性或者非平稳信号[21].另外,EMD方法不受Heisenberg 测不准原理[21]的限制,能够获得较高的分辨率.因此,EMD方法被广泛应用于机械振动和地震分析等领域.

基于互相关系数-峭度准则的EMD降噪方法中,互相关系数代表IMF分量与原始信号的相关度,其值越大,说明IMF分量与原始信号的相关度越高.因此,可以根据互相关系数辨别EMD分解过程中由于插值误差.端点效应以及过分解等诸多因素影响而产生的虚假分量.互相关系数的计算公式如下：

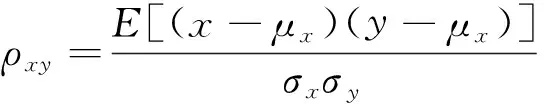
(1)

式中：E表示求数学期望；μx和μy分别为原始信号x和y的均值；σx和σy分别为原始信号x和y的标准差.

峭度是描述波形尖峰度的一个无量纲参数,其对信号的冲击成分非常敏感,即冲击成分比重越大,峭度值就越大.健康滚动轴承的振动信号峭度值分布接近正态分布,其值大约为3[16].当滚动轴承出现故障时,峭度值会明显增加,因此可以用峭度值衡量IMF分量中故障冲击成分的多少.峭度值可由下式计算：

(2)

EMD 互相关系数-峭度准则降噪方法根据互相关系数-峭度准则,筛选出相关系数较大并且峭度值大于3的IMF分量对信号进行重构,其他分量则被认为是伪分量或者噪声予以剔除.然而,噪声往往表现为高频信号,滚动轴承的高频共振信号会集中分布于前几个IMF分量.当信号的信噪比较低时,噪声起主导作用的IMF分量中也存在故障冲击成分.因此,单纯的根据互相关系数-峭度准则剔除峭度值小于3而互相关系数较大的IMF分量会造成重构信号丢失原有的故障冲击成分.

本文对故障滚动轴承变转速振动信号进行仿真(仿真信号的具体参数见3.1节),人为添加高斯白噪声和信噪比rSNB=-8 dB.采用基于瞬时故障特征频率的滚动轴承瞬时转频估计方法对转频进行估计(见图1),图1圆圈表示未经过降噪获取的IFCF趋势线,虚线代表通过瞬时故障特征频率趋势线和故障特征系数(仿真信号故障特征系数C=2)计算得到的瞬时转频,实线表示理论瞬时转频.其中t代表时间,f为频率.虽然估计的瞬时转频在一定程度上反映出理论转频的变化趋势,但是由于噪声干扰,估计的瞬时转频出现误差,其中最大差值为14.77 Hz,平均差值为9.36 Hz,严重影响了基于瞬时故障特征频率的滚动轴承瞬时转频估计方法的适用性.图2表示经过EMD互相关系数-峭度准则降噪后获取的IFCF趋势线、计算的瞬时转频以及理论瞬时转频,计算的瞬时转频(虚线)随时间的增加反而减小,与理论的瞬时转频(实线)相比,变化趋势完全相反.经过上述讨论可知：在低信噪比条件下,基于IFCF的滚动轴承瞬时转频估计方法受噪声干扰严重,需要对原始信号进行降噪预处理,而EMD互相关系数-峭度准则降噪方法容易造成滚动轴承振动信号中的故障冲击成分缺失,出现瞬时转频估计不准的现象.

图1　未经过降噪获取的瞬时转频和理论瞬时转频Fig.1　Calculated IRF without denoising and theoretical IRF

图2　基于EMD互相关系数-峭度准则降噪方法得到的瞬时转频和理论瞬时转频Fig.2　Calculated IRF with EMD cross-correlation coefficient and kurtosis criterion denoising and theoretical IRF

2EMD软阈值降噪

小波阈值降噪是由Donohon等[22-24]提出的一种降噪算法.其原理是原始振动信号经过小波变换之后,有用信号对应的小波系数较大,而噪声信号一般对应较小的小波系数,根据这一思想,通过选取合理的阈值对小波系数进行量化处理,以达到降噪的目的.小波阈值降噪主要包括以下3个基本步骤：1)选择小波基以及分解层次j,对信号进行分解；2)对从第1层到第j层的每一层高频系数,选择一个阈值进行阈值量化处理；3)根据小波分解的第j层低频系数和经过量化处理后的第1层到第j层的高频系数,进行小波重构.

小波阈值函数包括软阈值函数和硬阈值函数,其中软阈值处理信号相对平滑,软阈值函数[23]为

(3)

其中,N为某个尺度j的小波系数个数,J是小波分解的最大层次数.

然而,小波阈值去噪过程中最优分解层数不易确定,分解以及重构小波基函数选择不当同样会造成降噪效果不理想.滚动轴承瞬时转频估计方法中运用小波阈值降噪,步骤比较繁琐,不易得到最优降噪效果.

文献[25]提出将EMD与小波阈值降噪相结合用于齿轮故障模式识别与诊断,原理是采用小波阈值降噪处理高频IMF分量后与低频的IMF分量相加重构信号,最后通过时频分析完成齿轮的故障诊断,并取得了较好的效果.然而,仅根据文献[25]无法确定如何选择需要降噪的IMF分量以及选择几个高频IMF分量做降噪处理,小波阈值降噪函数也没有具体指出.另外,由于EMD算法本身的缺陷,容易产生伪分量,将阈值去噪后的IMF分量与其余IMF直接相加也会忽略低频噪声信号和伪分量对重构信号的影响.为此,本文将EMD互相关系数-峭度准则降噪与小波软阈值降噪相结合,设定互相关系数阈值θ=0.1,剔除互相关系数ρxy<0.1的IMF分量,对互相关系数ρxy≥0.1而峭度值小于3的IMF分量进行软阈值降噪,将降噪后IMF分量与剩余的IMF分量相加得到重构信号.对于预设的互相关系数阈值,本文经过多次试验对比确定其值为0.1较为合理,选取互相关系数大于0.1的IMF分量进行后续处理,既能去除EMD分解过程中由于插值误差和过分解等诸多因素而产生的虚假分量,也能避免含有轴承信息的IMF分量的缺失.本文选取峭度值3作为分界点(第一章已经指出,健康轴承的峭度值成正态分布,其值大约为3,当滚动轴承出现故障时,峭度值会明显增加).因此峭度值大于3的IMF分量轴承故障冲击较为明显,无须进一步降噪处理；而峭度值小于3的IMF分量由于噪声信号的干扰轴承的故障特征不明显,需要进行降噪处理以突出故障信息.

根据式(3)给出本文所用到的软阈值函数公式：

(4)

式中：ηj表示第j个IMF分量的函数式,γj为第j个IMF分量的阈值，计算公式如下：

EMD软阈值降噪算法的步骤如下,具体的流程图如图3所示.1)对原始信号进行EMD分解得到IMF分量；2)计算各IMF分量与原始信号的互相关系数以及各IMF分量的峭度值；3)根据互相关系数-峭度准则选出需要进行阈值降噪的IMF分量以及剔除伪IMF分量；4)对选定的IMF分量进行阈值降噪后与剩余的IMF分量相加得到重构信号.

图3　经验模态分解(EMD)软阈值降噪流程图Fig.3　Flowchart of empirical mode decomposition (EMD) soft-thresholding denoising

EMD软阈值降噪方法的优点主要包括：1)具备EMD的自适应性、多分辨率、完备性等优势;2)确保噪声起主导作用并且含故障冲击成分的IMF分量不被剔除;3)避免了小波最优分解层数的选择,同时也避免了小波分解过程中小波基函数选择的繁琐性,从而更容易对滚动轴承非平稳振动信号进行降噪处理.

3仿真与实测信号验证

3.1仿真信号分析

为了验证本文降噪方法在低信噪比条件下滚动轴承瞬时转频估计中的有效性,首先对故障轴承变转速振动信号进行仿真.故障轴承非平稳信号构造公式[26]如下：

sin[wr(t-tm)]}.

(5)

式中：Am表示由故障引起的第m个冲击的幅值;β为结构衰减系数;wr为由轴承故障引起的共振频率;u(t)为单位阶跃函数;tm为第m个冲击发生的时间,可由递推下式确定：

t1=(1+μ)·1/f(t0)/n,

tm=(1+μ)·1/f(tm-1)/n,m=2,3,…,M.

(6)

式中：f(t)是轴承转频随时间的变化规律；t0=0；n为每转出现的故障冲击数.

本文根据式(6)对故障轴承低信噪比非平稳信号进行仿真,如下式：

gb=g(t)+n(t).

(7)

式中：Am与时间成线性变化,轴承瞬时转频随时间的变化规律设定为f(t)=10(t)+30,系统的共振频率wr=3 500Hz,衰减系数β=8,采样频率Fs=5 000 Hz,采样点数为20 000,故障特征系数C=2；n(t)为高斯白噪声,信噪比rSNB=-8 dB.仿真信号的时域波形图如图4所示,U为电压幅值.

图4　仿真信号的时域波形图Fig.4　Simulated vibration signal in time domain

图5　前6个IMF分量(IMF1-6)Fig.5　Intrinsic mode functions (IMF1-6)

根据重构信号对滚动轴承的瞬时转频进行估计,具体步骤如下：1)通过重构信号的快速谱峭度图,确定带通滤波器参数进行带通滤波；2)对滤波信号进行Hilbert变换以及STFT变换获取包络时频图,利用基于幅值累加的峰值搜索算法从包络时频图中提取瞬时故障特征频率并对其拟合得到瞬时故障特征频率趋势线；3)瞬时故障特征频率趋势线与故障特征系数相除即可得到瞬时转频.图6(a)给出了获取的瞬时故障特征频率趋势线、计算的滚动轴承瞬时转频与理论瞬时转频的对比,理论瞬时转频f(t)=10(t)+30,估计的瞬时转频与其相吻合,其中两者的最大差值为2.00 Hz,平均差值为1.03 Hz.分别采用本文降噪方法、EMD互相关系数-峭度准则降噪方法以及未采用降噪方法估计的滚动轴承瞬时转频如图6(b)所示.其中方块表示经EMD软阈值降噪后估计的瞬时转频,虚线表示经过EMD互相关系数-峭度准则降噪后获取的瞬时转频,圆圈表示未降噪直接从原始信号中估计的瞬时转频,实线为理论瞬时转频.通过综合对比可知,单纯的采用EMD互相关系数-峭度准则降噪方法对原始信号进行预处理容易造成信号中的故障冲击成分的缺失,出现瞬时转频估计不准现象；EMD软阈值降噪优于EMD互相关系数-峭度准则降噪方法,保证信号完整性的同时,降低了噪声干扰,突出了信号的故障信息,进而瞬时转频的估计结果更接近理论值.

表1IMF1-IMF7与原始信号的互相关系数及其各自峭度值和IMF′的峭度值

Tab.1Cross-correlation coefficients and kurtosis values of IMF1-IMF7 and IMF′ kurtosis values

IMF序号互相关系数KIMFIMF'IMF10.72442.54313.8331IMF20.47663.3816—IMF30.30892.96164.6204IMF40.21633.0943—IMF50.15142.87054.4870IMF60.11192.80393.0255IMF70.07283.1745—

图6　本文算法获取的转频及其与传统算法的综合比对Fig.6　Calculated IRF by proposed algorithm and comparison with traditional algorithms

3.2实测信号分析

为进一步验证EMD软阈值降噪在实际工况低信噪比非平稳条件下估计滚动轴承瞬时转频方法中的实用性,利用北京交通大学机电学院现代制造技术综合实验中心ST-5000A型多功能柔性转子试验台(见图7)进行实测验证.该试验台由速度调节器控制电机转速,加速度传感器安装在离轴承较近的位置以准确的测量其振动信号,转速计安装在最右侧用于测量转速,采集装置为YE6231采集卡及其配套的采集软件.采集卡以相同采样率同时采集两路信号,一路为滚动轴承故障信号,另一路为故障信号相对应的转速脉冲信号.利用电火花切割凹槽模拟轴承外圈早期裂纹故障,实验轴承型号为6 000.该轴承的滚珠个数为7，滚动体直径为4.8 mm,节圆直径为17.65 mm,接触角为0.根据其几何参数计算出外圈故障特征系数Co=2.548.实测信号的时域波形图如图8所示,采样率为24 000 Hz,采样时长为2 s,瞬时转频随时间增加而逐步增加.根据图8可知,由于滚动轴承的故障轻微,故障冲击淹没在背景噪音中,表现不明显.

图7　滚动轴承试验台布局Fig.7　Experimental setup of rolling element bearing

图8　实测信号的时域波形图Fig.8　Raw vibration signal in time domain

图9　本文算法获取的转频及其与传统算法的综合比对Fig.9　Calculated IRF by proposed algorithm and comparison with traditional algorithms

根据基于瞬时故障特征频率的滚动轴承瞬时转频估计方法,从未降噪的滚动轴承实测信号中获取的瞬时故障特征频率趋势线,使其与故障特征系数Co=2.548相除得到的滚动轴承的瞬时转频,以及通过转速计实测的瞬时转频分别如图9(a)所示.其中,实测的瞬时转频首先根据转速计测取的脉冲信号计算出离散的转速点,进而通过曲线拟合所得到.实测的瞬时转频直接由硬件测量计算而来,与振动信号具有同步性,因此理论上可以作为验证本文算法的标准.根据图9(a)易知,估计的瞬时转频有明显的误差,其中最大差值约为46.10 Hz,平均差值为28.05 Hz.图9(b)表示根据互相关系数-峭度准则进行EMD降噪后得到的瞬时故障特征频率趋势线、计算得到的滚动轴承瞬时转频以及实测的瞬时转频. 可知，估计的瞬时转频与实测值的变化趋势不符,出现了明显失真现象,没有参考价值.利用本文方法对滚动轴承实测信号进行降噪后获取的瞬时故障特征频率趋势线、计算得到的瞬时转频以及实测的瞬时转频分别如图9(c)所示,估计的瞬时转频准确的反应了实测瞬时转频的变化趋势,数值与实测值十分接近,最大差值约为6.30 Hz,平均差值约为2.60 Hz.图9(d)表示实测瞬时转频以及分别利用3种方法估计得到的瞬时转频,其中,方块表示经EMD软阈值降噪后估计的瞬时转频,虚线表示经过EMD互相关系数-峭度准则降噪后获取的瞬时转频,圆圈表示未降噪直接从原始信号中估计的瞬时转频,实线为实测瞬时转频.通过对滚动轴承实测振动信号分析进一步说明：EMD软阈值降噪算法优于EMD互相关系数-峭度准则降噪算法,避免了重构信号的失真,具有较好的降噪效果,适用于变转速条件下故障轴承的瞬时转频估计.

4结语

对仿真信号分析的结果表明,该方法能够保证信号完整性的同时,突出了故障信息,降低了噪声干扰,进而提高了瞬时转频估计的准确性.本文对早期故障滚动轴承变转速条件下的实测信号进行了分析,采用EMD软阈值降噪后估计的瞬时转频的误差明显减小,进一步验证了本文方法在滚动轴承瞬时转频估计方法中信号预处理的有效性.因此，该方法在低信噪比条件下的滚动轴承转频估计方面具有较好的应用前景.

参考文献(References):

[1] MING Z, JING L, WANG X F, et al. A tacho-less order tracking technique for large speed variations[J]. Mechanical Systems and Signal Processing, 2013, 40(1): 76-90．

[2] BONNARDOT F,BADAOUI E M, RANDALL R B, et al. Use of the acceleration signal of a gearbox in order to perform angular resampling (with limited speed fluctuation)[J]. Mechanical Systems and Signal Processing, 2005, 19 (4): 766-785．

[3] URBANEK J, BARSZCZ T, ANTONI J. A two-step procedure for estimation of instantaneous rotational speed with large fluctuations [J]. Mechanical System and Signal Processing, 2013, 38:96-102．

[4] COMBET F, ZIMROZ R. A new method for the estimation of the instantaneous speed relative fluctuation in a vibration signal based on the short time scale transform[J].Mechanical System and Signal Processing, 2009,23: 1382-1397．

[5] ZHAO D Z, LI J Y, CHENG W D. Feature extraction of faulty rolling element bearing under variable rotational speed and gear interferences conditions[J]. Shock and Vibration, 2015,2015:1-9．

[6] BOASHASH B. Interpreting and estimating the instantaneous frequency of a signal-Part1: fundamentals [J]. Proceedings of the IEEE, 1992, 80(4):520-538．

[7] BOASHASH B. Interpreting and estimating the instantaneous frequency of a signal-Part 2: algorithms and applications [J]. Proceedings of the IEEE, 1992, 80(4):540-568. [8] 郭瑜, 秦树人, 汤宝平, 等.基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报, 2003,39(3):32-36．

GUO Yu, QIN Shu-ren, TANG Bao-ping, et al. Order tracking of rotating machinery based on instantaneous frequency estimation [J].Chinese Journal of Mechanical Engineering, 2003, 39(3):32-36．

[9] 赵晓平,赵秀莉,侯荣涛,等.一种新的旋转机械升降速阶段振动信号的瞬时频率估计算法[J].机械工程学报,2011,47(7):103-108．

ZHAO Xiao-ping, ZHAO Xiu-li, HOU Rong-tao, et al.A new method for instantaneous frequency estimation of run-up or run-down vibration signal for rotating machinery[J]. Chinese Journal of Mechanical Engineering, 2011, 47(7):103-108．

[10] WANG T Y, LIANG M, LI J Y, et al. Rolling element bearing fault diagnosis via fault characteristic order (FCO)analysis[J].Mechanical System and Signal Processing, 2014, 45(1): 139-153.[11] DONG G M, CHEN J, ZHAO F G, A frequency-shifted bispectrum for rolling element bearing diagnosis [J]. Journal of Sound and Vibration, 2015, 339:396-418．

[12] WANG J, HE Q B, KONG F R. An improved multiscale noise tuning of stochastic resonance for identifying multiple transient faults in rolling element bearings[J]. Journal of Sound and Vibration, 2014, 333(26):7401-7421．

[13] 冯辅周,司爱威,饶国强,等. 基于小波相关排列熵的轴承早期故障诊断技术[J]. 机械工程学报,2012,48(13): 73-79．

FENG Fu-zhou, SI Ai-wei, RAO Guo-qiang, et al. Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy [J]. Journal of Mechanical Engineering, 2012, 48(13): 73-79．

[14] 王仲生, 姜洪开, 徐一艳. 发动机转子系统早期故障智能诊断[J]. 航空学报,2009,30(2):242-246．

WANG Zhong-sheng, JIANG Hong-kai, XU Yi-yan. Early fault intelligent diagnosis of aero-engine rotor systems [J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(2):242-246．

[15] 胥永刚, 马海龙, 付胜, 等. 机电设备早期故障微弱信号的非线性检测方法及工程应用[J]. 振动工程学报,2011,24(5):529-538.

XU Yong-gang, MA Hai-long, FU Sheng, et al. Theory and applications of weak signal non-linear detection method for incipient fault diagnosis of mechanical equipments [J]. Journal of Vibration Engineering, 2011, 24(5):529-538.

[16] 苏文胜,王奉涛,张志新,等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击,2010,29(3): 18-21．SU Wen-sheng, WANG Feng-tao, ZHANG Zhi-xin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearing [J]. Journal of Vibration and Shock, 2010, 29(3):18-21．

[17] 彭畅,柏林,谢小亮. 基于EEMD、度量因子和快速谱峭度图的滚动轴承故障诊断方法[J].振动与冲击2012, 31(20):144-146．

PENG Chang, BO Lin, XIE Xiao-liang. Fault diagnosis method of rolling element bearing based on EEMD, measure-factor and fast kurtogram[J].Journal of Vibration and Shock, 2012, 31(20): 144-146. [18] 唐贵基,王晓龙.基于EEMD降噪和1.5维能量谱的滚动轴承故障诊断研究[J].振动与冲击, 2014,33(1):6-10．

TANG Gui-ji, WANG Xiao-long. Fault diagnosis for roller bearings based on EEMD de-noising and 1.5-dimensional energy spectrum [J]. Journal of Vibration and Shock, 2014, 33(1):6-10．

[19] 程正兴,杨守志,冯晓霞.小波分析的理论、算法、进展与应用[M].北京:国防工业出版社,2007:332-335．

[20] BADOUR A F, SUNAR M, CHEDED L. Vibration analysis of rotating machinery using time-frequency analysis and wavelet techniques [J].Mechanical Systems and Signal Processing,2011,25(6): 2083-2101．

[21] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London,1998, 454(1971):903-995．

[22] DONOHO D L, JOHNSTONE I M. Threshold selection for wavelet shrinkage of noisy data [J].Engineering in Medicine and Biology Society, 1994, 1:A24-A25．

[23] DONOHO D L. Denoising by soft-thresholding[J]. IEEE Transaction on Information Theory, 1995, 41(3):613- 627．

[24] DONOHO D L, JOHNSTONE I. Wavelet shrinkage asymptotic [J].Journal of Royal Statistical Society, 1995, 57(2):301-369．

[25] 邵忍平,曹精明,李永龙.基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J].振动与冲击,2012,31(8):96-101．

SHAO Ren-ping, CAO Jing-ming, LI Yong-long. Gear fault pattern identification and diagnosis using time- frequency analysis and wavelet threshold de-noising based on EMD [J].Journal of Vibration and Shock, 2012, 31(8):96-101．

[26] 王天杨, 李建勇, 程卫东.基于改进的自适应噪声消除和故障特征阶比谱的齿轮噪源干扰下变转速滚动轴承故障诊断[J].振动与冲击, 2014,33(18):7-13．

WANG Tian-yang, LI Jian-yong, CHENG Wei-dong. Fault diagnosis of rolling bearing under a variable rotational speed and gear vibration noise based on revised ANC algorithm and FCO spectrum [J]. Journal of Vibration and Shock, 2014, 33 (18):7-13．

DOI:10.3785/j.issn.1008-973X.2016.03.005

收稿日期：2015-04-10.

基金项目：国家自然科学基金资助项目(51275030).

作者简介：程卫东(1967-), 男，副教授，从事制造装备智能测控与故障诊断教学科研工作.ORCID:0000-0001-5085-4758. E-mail: wdcheng@bjtu.edu.cn

中图分类号：TH 113.1

文献标志码：A

文章编号：1008-973X(2016)03-08-0428

EMD soft-thresholding denoising algorithm for rolling element bearing rotational frequency estimation

CHENG Wei-dong, ZHAO De-zun

(SchoolofMechanicalElectronicandControlEngineering,BeijngJiaotongUniversity,Beijing100044,China)

Abstract:A method based on the empirical mode decomposition (EMD) and wavelet shrinkage was proposed due to the shortcomings of the EMD cross-correlation coefficient and kurtosis criterion denoising and wavelet shrinkage. The method consists of four main steps: (i) IMFs were obtained by decomposing raw signal, (ii) The cross-correlation coefficient between IMFs and the raw signal, and the kurtosis values of the IMFs were calculated, (iii) IMFs with the noise were selected and the false IMFs were removed, (vi) the noise of the selected IMFs was removed by the soft-thresholding denoising method, and then the signal with the rest of the IMFs was reconstructed. The proposed method was tested based on both the simulated and experimental bearing vibration signals. Results show that, compared with EMD cross-correlation coefficient and kurtosis criterion denoising, the method of EMD soft-thresholding denoising can ensure the integrity of the signal, highlight fault features and reduce the error of the instantaneous rotational frequency (IRF).

Key words:empirical mode decomposition (EMD); soft-thresholding denoising; rolling element bearing; signal preprocessing; instantaneous rotational frequency (IRF) estimation