机械系统的故障演化测试性建模及预计

谭晓栋,罗建禄,李　庆,邱　静

(1.武警警官学院 电子技术系, 四川 成都 610213;2.国防科学技术大学 装备综合保障国防科技重点实验室, 湖南 长沙 410073)



机械系统的故障演化测试性建模及预计

谭晓栋1,2,罗建禄1,李庆1,邱静1

(1.武警警官学院 电子技术系, 四川 成都 610213;2.国防科学技术大学 装备综合保障国防科技重点实验室, 湖南 长沙 410073)

摘要:采用部件级及系统级的分层建模思想，提出基于故障演化的测试性建模方法.在部件级,分析系统的故障演化机理,建立描述系统故障与征兆参数的定性相关性矩阵；在系统级,使用键合图的分析方法,建立系统中部件故障与子系统以及系统参数间的能量传递关系,进而获得征兆参数与测试间的动力学关系.在考虑故障可检测率、故障可隔离率的基础上,以故障可预测率以及故障可跟踪率分别描述系统对故障的检测、隔离、预测和跟踪的测试性水平.案例分析结果表明：故障与征兆参数的定性关系以及征兆参数与测试的动力学关系能准确刻画机械系统中故障演化与测试的关系,在此基础上提出的测试性预计方法能够有效评估机械系统对故障的检测、隔离、跟踪和预测能力,有助于提高机械系统对故障演化的跟踪和对失效的预测水平.

关键词：测试性建模及预计；测试性设计；故障-测试相关性；键合图

机械系统被广泛应用于航空(如：机、飞艇等)、航天、航海等领域[1-2].由于长期工作在恶劣的环境下,同时还必须满足各种工作任务的要求,机械系统极易发生故障,进而导致任务的中断,严重的故障将会造成重大的财产损失和人员伤亡[3-5].为了确保系统在各种环境、工况、不同工作模式下健康、稳定运行,尽可能降低系统运行成本,避免由于突发失效引起的灾难事故的发生,要求系统具有实时监控其关重件性能退化、跟踪关键故障演化的能力,以保证在失效发生前有效评估其健康状态,进而触发维修决策机制[6-8].采用各种传感器或检测方法是有效实现健康监控和健康评估的基础[9-10],因此,对机械传动系统开展测试性设计(designfortestability,DFT)显得尤为重要,测试性模型和测试性预计是DFT的前提和基础[11-12].

当前,主流的测试性模型为信息流模型和多信号流图模型,这2种模型都是基于布尔关系的故障-测试相关性矩阵建立的,主要用于电子系统的故障检测和隔离[13-14].由于电子系统各个模块或元件间具有较强耦合性,故障与测试间的这种布尔关系能比较准确地描述电子系统中故障的传播关系[12].然而,对于机械传动系统而言,由于系统中的各个模块和单元间相互耦合,导致故障间关系、故障与测试节点之间的关系复杂,布尔关系的故障-测试矩阵往往不能准确描述故障间及故障与测试节点之间的关系.此外,针对电子系统的测试性预计方法主要基于系统中故障-测试布尔相关性矩阵,计算出系统固有测试性指标(如:故障检测率、故障隔离率、虚警率等),这些测试性指标主要用于评估系统对故障的检测和隔离水平[15].为了避免由于部件突发失效造成的事故,就要求系统的传感器或测试手段能有效地监控或跟踪系统中故障的演化过程.因此,机械系统的测试性预计的内容需要进行扩展,即不仅要评估系统对故障的检测和隔离能力,还需要评估出系统对故障演化过程的跟踪能力以及对故障的预测能力.

基于此,本文结合传统测试性模型的优点以及键合图的相关理论,提出定性和定量相结合的故障演化测试性建模(faultevolutiontestabilitymodeling,FETM)方法和基于FETM的测试性预计方法.

1故障演化测试性建模理论

在机械传动系统中故障模式(如：齿轮裂纹)的演化过程中,与故障严重度相关的故障征兆(如：振动加剧、温度升高、油液颗粒度增加等)会在其造成被测单元(unitundertest,UUT)功能失效前提前表现出来.通过系统中的测试节点监控那些与故障严重程度相关的征兆参数可以有效地跟踪故障演化并为健康状态评估和故障预测提供数据支持.在从正常工作状态经过性能退化直至UUT功能失效的过程中,描述UUT健康程度的状态参数会随着UUT性能下降提前表现出来,通过在系统中布置测试节点监测这些状态参数能有效跟踪UUT性能退化过程并指导评估系统中UUT的健康状态.本文提出的FETM采用部件层级及系统层级的分层建模思想,主要建模策略如图1所示.

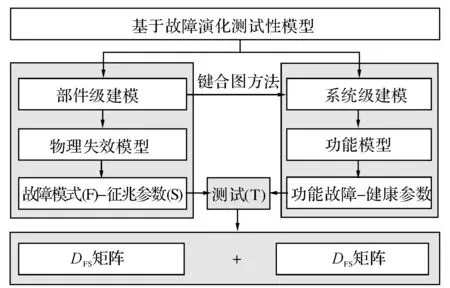
图1　故障演化测试性建模策略Fig.1　Fault evolution testability model (FETM) modeling process

在部件级,考虑部件结构及材料属性,分析发生在部件上的失效或退化的根本原因.根据材料属性、几何尺寸、边界条件、运行状态等建立不同结构及材料的下部件的损伤机制,为建立结构及材料的物理失效模型奠定基础.根据构建的退化或物理失效模型,为每个故障模式定义与其故障演化过程(表征故障大小)相关的故障征兆参数,进而建立描述系统故障与征兆参数的定性相关性矩阵DFS,描述系统中故障模式与故障征兆的布尔映射关系：

s1s2…sN

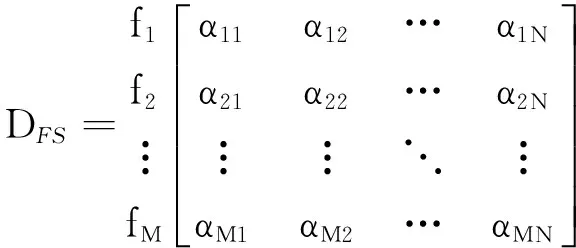
(1)

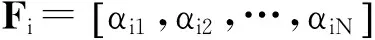
S(fi)={sj|sj∈S, αij=1}.

在系统级,使用键合图的方法为系统中每个UUT定义相应的键合图属性,建立系统中部件、子系统以及系统间的能量传递关系[16-17].根据故障演化机理,使用物理规律建立系统中部件的故障或退化的动态行为(故障征兆)以及系统性能参数与系统物理测试节点的定量关联关系,进而建立描述故障征兆参数与测试节点的相关性矩阵DST.

t1t2…tN

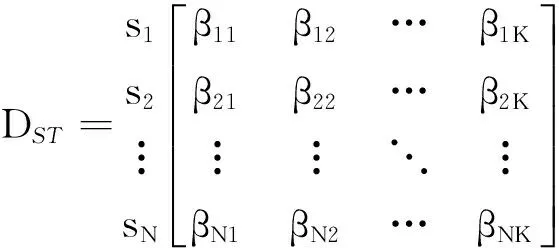
(2)

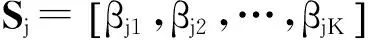
DFS及DST2个矩阵描述了系统中可利用测试节点与故障演化过程中征兆参数间的关联关系,以上关联关系是指导测试性预计的基础.

2基于FETM的测试性预计

测试性预计主要目的是以FETM为基础,根据系统中测试与故障演化的关联关系,预计系统对故障的检测和隔离、故障演化过程的跟踪能力和对故障的预测能力.定义系统中UUT集合U={ u1,u2,…,ui,…,uH},描述系统中UUT健康程度所有状态参数集合为C={c1,c2,…,cj,…,cZ},第i个UUT对应的状态参数集合为C(ui)={ci|ci∈C,αij=1},系统中所有的故障模式集F={f1,f2,…,fi,…,fM},对应的故障模式的故障率集合R={λ1,λ2,…,λM},同时定义FG及FS分别为系统中渐变及突变故障模式集合.显然有F=FG∪FS.故障征兆集S={s1,s2,…,sj,…,sN},定义一个故障征兆对应一个状态参数.故障模式fi对应的所有征兆集合S(fi)={sj|sj∈S,αij=1}.系统中可利用的测试集T={t1,t2,…,tk,…,tK}.系统中能被检测到的故障征兆集合SD={sj|βjk≠0}.系统中能被辨识的故障征兆集合SI={sj|sj∈SD, ∀j1≠j2,Tj1⊕Tj2=1}, Tj1、Tj2分别为DST矩阵中的第j1和j2行向量(1≤j1,j2≤N,‘⊕’为异或操作符).

1)可检测的故障模式.在故障模式fi对应的征兆集S(fi)中,至少一个故障征兆能被系统检测到,则称fi为可检测故障模式；否则,fi为不可检测故障模式.系统中可被检测的故障模式集合FCD={fi|fi∈F,∀sj∈S(fi),βjk≠0},可被检测的故障模式数NCD=|FCD|.不可检测的故障模式集FUCD=F-FCD.

2)可隔离的故障模式.在故障模式fi对应的征兆集S(fi),至少一个故障征兆能被系统辨识,则称fi为可隔离故障模式；否则,fi为不可隔离故障模式.系统中可被隔离的故障模式集合FCL={fi|fi∈FCD,∀sj∈S(fi),∃sj∈SI},系统中可被隔离的故障模式数NCL=|FCL|.不可隔离的故障模式集是指具有相同故障征兆特征,不能被唯一隔离的故障组FUCD=FCD-FCL.

3)可跟踪的故障模式.在故障模式fi对应的征兆集S(fi)中,所有的征兆参数都能被检测到,则称fi为可跟踪故障模式；否则,fi为不可跟踪故障模式.系统中可被跟踪的故障模式集合FCT={fi|fi∈FG,∀sj∈S(fi),βjk≠0},1≤i≤M,1≤j≤N,1≤k≤K.可被跟踪的故障模式数NCT=|FCT|.不可跟踪的故障模式集FUCT=FCD-FCT.

4)可预测的故障模式.在故障模式fi对应的征兆集S(fi),所有的征兆参数都能被辨识到,则称fi为可预测故障模式；否则,fi为不可预测故障模式.系统中可被预测的故障模式集FCP={fi|fi∈FG,∀sj∈S(fi),sj∈SI}.可被预测的故障模式数NCP=|FCP|.不可预测的故障模式集FUCP=FCD-FCP.

5)冗余测试TR.是指检测能力相同的测试,表示在DST矩阵中相同列的测试集合.TR={tk|tk∈T, ∀k1≠k2, Tk1⊕Tk2=0},Tk1,Tk2分别表示DST矩阵中的k1和k2行,1≤k1,k2≤K.

为了衡量系统对故障的检测、隔离、跟踪和预测能力,除了故障可检测率rfd(faultdetectionrate)和故障可隔离率rfi(faultisolationrate)外[15],本文新定义了故障可跟踪率rft(faulttrackingrate)和故障可预测率rfp(faultpredictionrate)2个指标分别评估系统对故障的可跟踪能力和对故障的可预测能力.

定义1 故障可跟踪率rft定义为可跟踪故障数与系统中可被检测的故障数之比,其数学表达式为

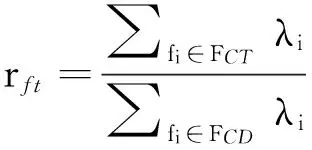
(3)

故障可跟踪率描述为系统内部的测试手段或监测系统对故障演化过程中表征故障严重程度的征兆参数的跟踪与监控能力,是系统固有的测试性设计属性,主要应用在测试性设计阶段.

定义2故障可预测率rfp定义为系统中可被预测的故障数与系统中可被检测的故障数之比,其数学表达式为

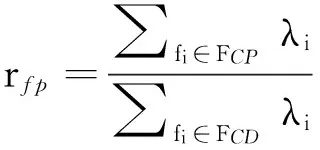
(4)

在对系统测试性设计中,可以计算出系统的rfd、rfi、rft、rfp等测试性指标.若以上指标达不到系统预定的要求,或者存在大量的模糊组,则需要针对不可测故障集、不可隔离故障集、不可跟踪故障集及不可预测故障集中的故障追加测试,若发现有冗余的测试,则要剔除掉.上述工作要在FETM上进行,改进测试性设计后,模型还需要相应的修改.再利用更新后模型生成的相关性矩阵进行测试性预计,直到测试性指标满足系统要求.

3案例分析

齿轮传动系统广泛应用于大型武器装备的动力传动系统中,由于工作环境恶劣,系统中的主要传动部件(如：轴承、齿轮等)极易发生故障[19].经过大量数据统计表明,由于齿轮传动系统故障导致的装备功能失效占总数的30%以上[20].大量经验表明,为了实现对系统的健康监控,过多的测点会极大的增加测试费用,同时会降低系统的可靠度,然而过少的测点不能达到预定的测试性指标要求,同时会导致系统故障的漏检[15].

一阶齿轮传动系统主要包括驱动电机、联轴器、齿轮轴、轴承、主动齿轮、被动齿轮等.其中,驱动电机主要包括定子、转子、电机轴承、电机轴等.根据系统的功能组成,构建如图2所示的齿轮传动系统的键合图,Se为电压源,R为阻性元件,I为惯性元件,C为容性元件,TF为转换器,“0”为共势结,“1”为共流结,“K”为自感系数,E为电源电压,UR为定子电压,La为定子电感系数,if为绕组电流,Rf为绕组电阻,ia为电枢电流,Ra为电枢电阻,Ψ为流经绕组的磁通,Rm为外部干扰电阻,Jm为机械负载部件总的转动惯量,Mm为负载部件的扭矩,T为电机轴输出扭矩,ω0为电机轴角速度,k1为联轴器刚度,ω1为主动齿轮角速度,J1为主动齿轮转动惯量,μ1为主动齿轮阻尼系数,z1为主动齿轮齿数,z2为被动齿轮齿数,ω2为被动齿轮角速度,J2为被动齿轮转动惯量,μ2为被动齿轮阻尼系数,Mload为负载扭矩.键合图元的相关定义如表1所示,根据功能流理论,建立如下的状态方程：

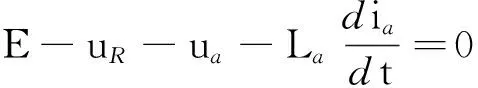
(5)

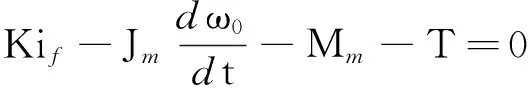
(6)

结合系统的功能结构,获得一阶齿轮箱系统的部分故障演化分析的结果[21],如表2所示.根据第2章介绍的FETM建模方法,构建如图3所示的一阶齿轮箱系统的FETM.结合图2及式(5)和(6),使用MATLAB/Simulink工具箱建立一阶齿轮箱系统的故障仿真模型,如图4所示.

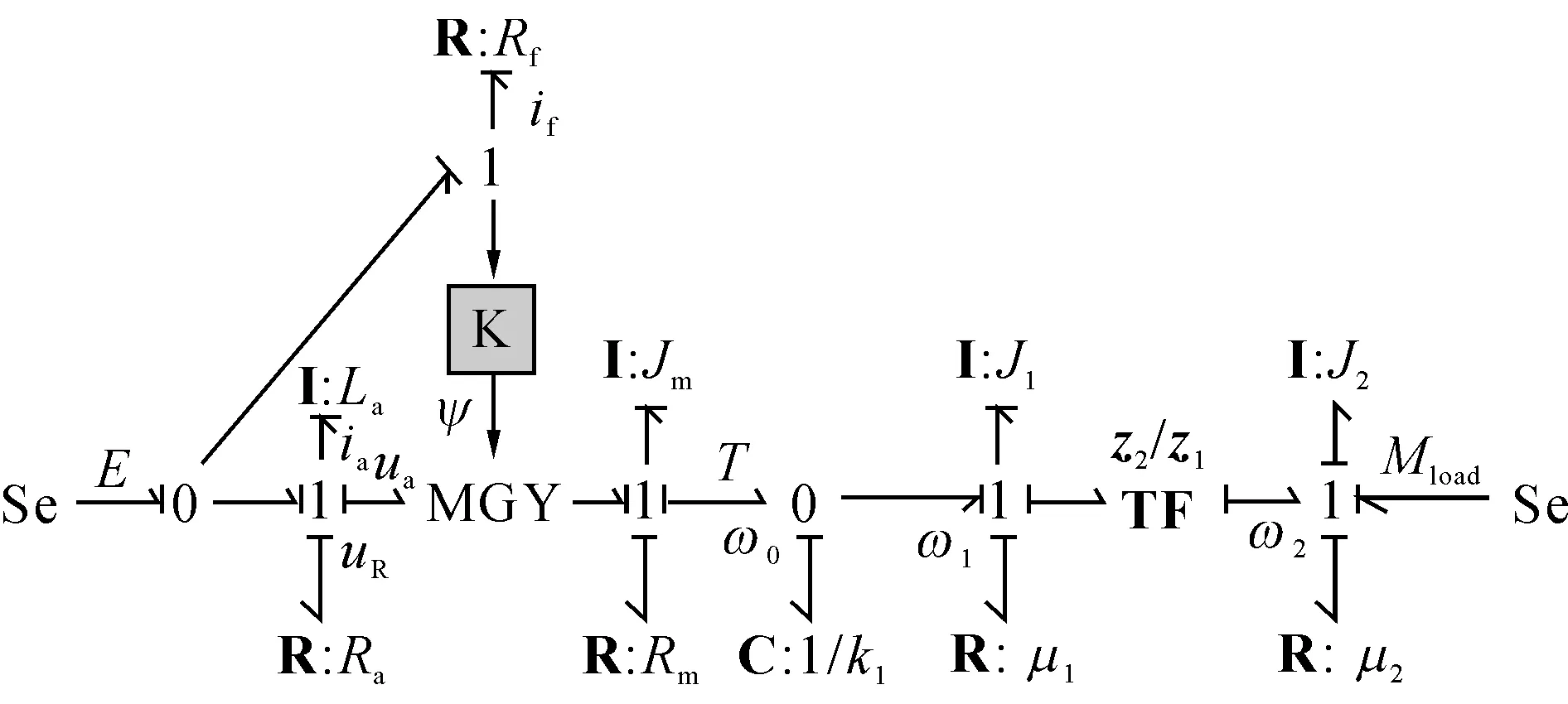
图2　一阶齿轮箱系统的键合图Fig.2　Bond graph of one-stage gearbox system

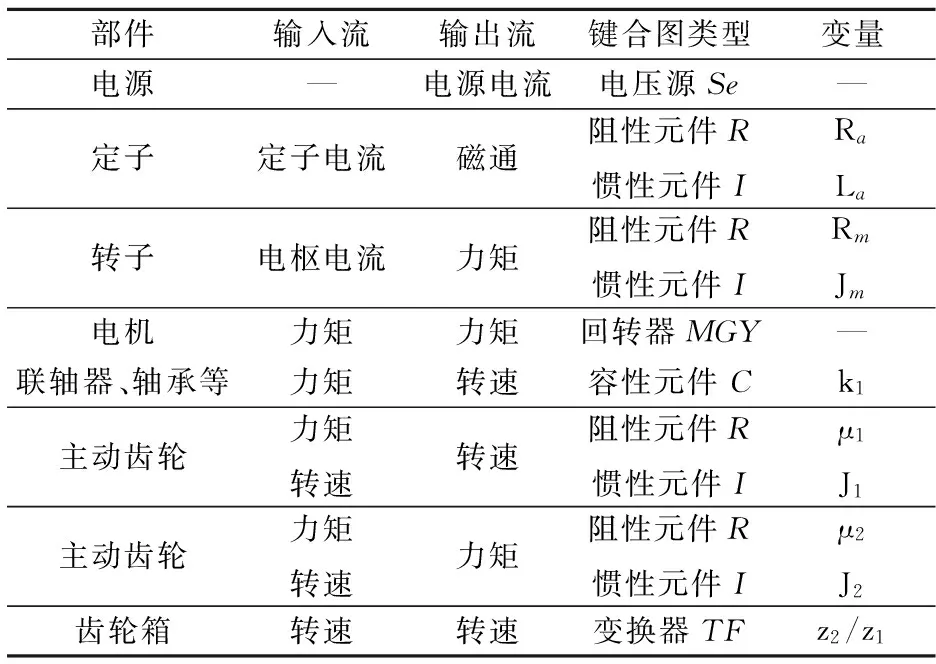
部件输入流输出流键合图类型变量电源—电源电流电压源Se—定子定子电流磁通阻性元件R惯性元件IRaLa转子电枢电流力矩阻性元件R惯性元件IRmJm电机力矩力矩回转器MGY—联轴器、轴承等力矩转速容性元件Ck1主动齿轮力矩转速转速阻性元件R惯性元件Iμ1J1主动齿轮力矩转速力矩阻性元件R惯性元件Iμ2J2齿轮箱转速转速变换器TFz2/z1

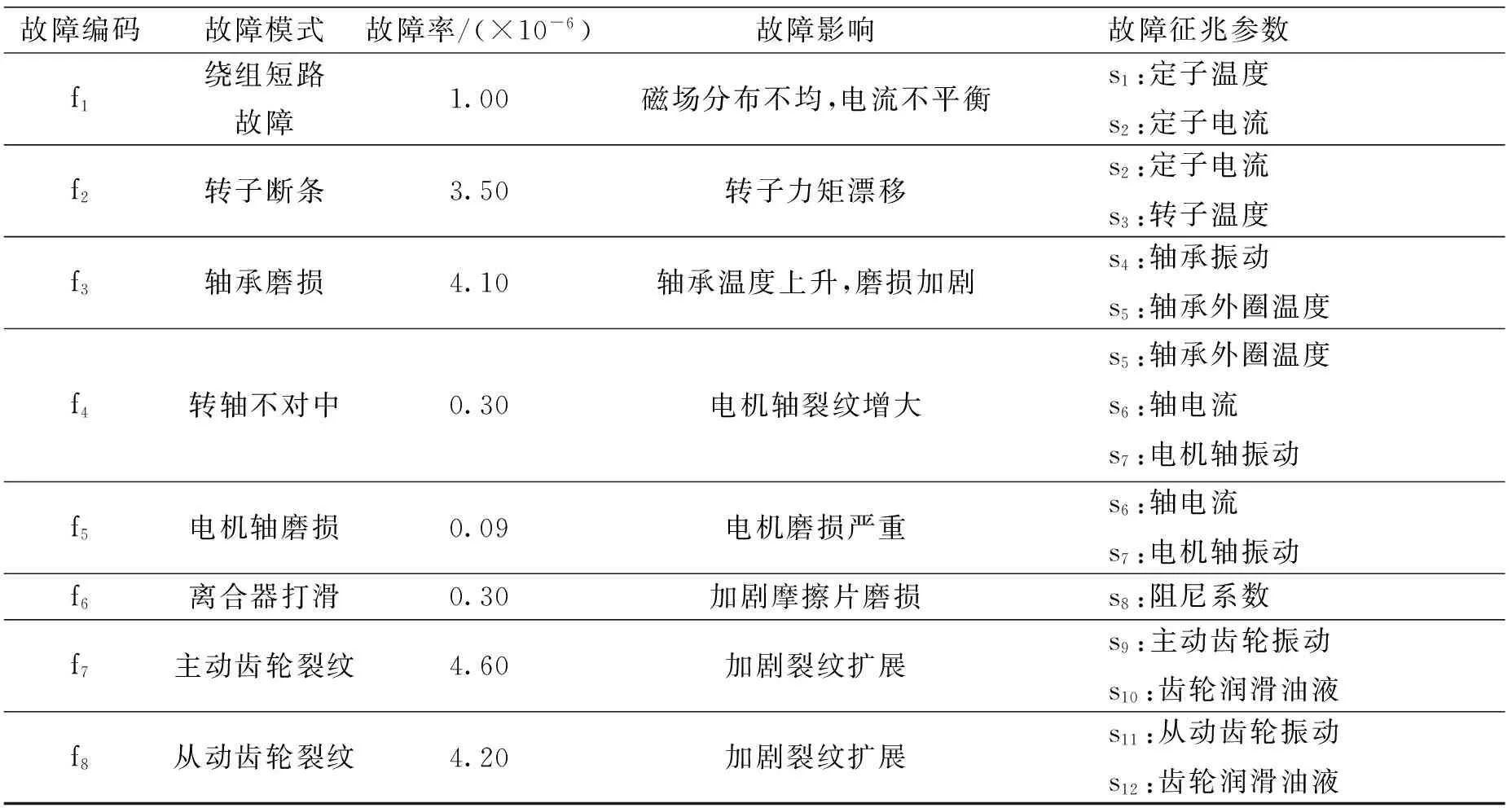
表2　部分故障演化分析结果

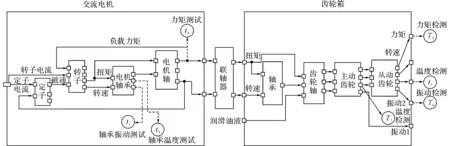
图3　一阶齿轮箱系统的FETMFig.3　FETM of one-stage gearbox system

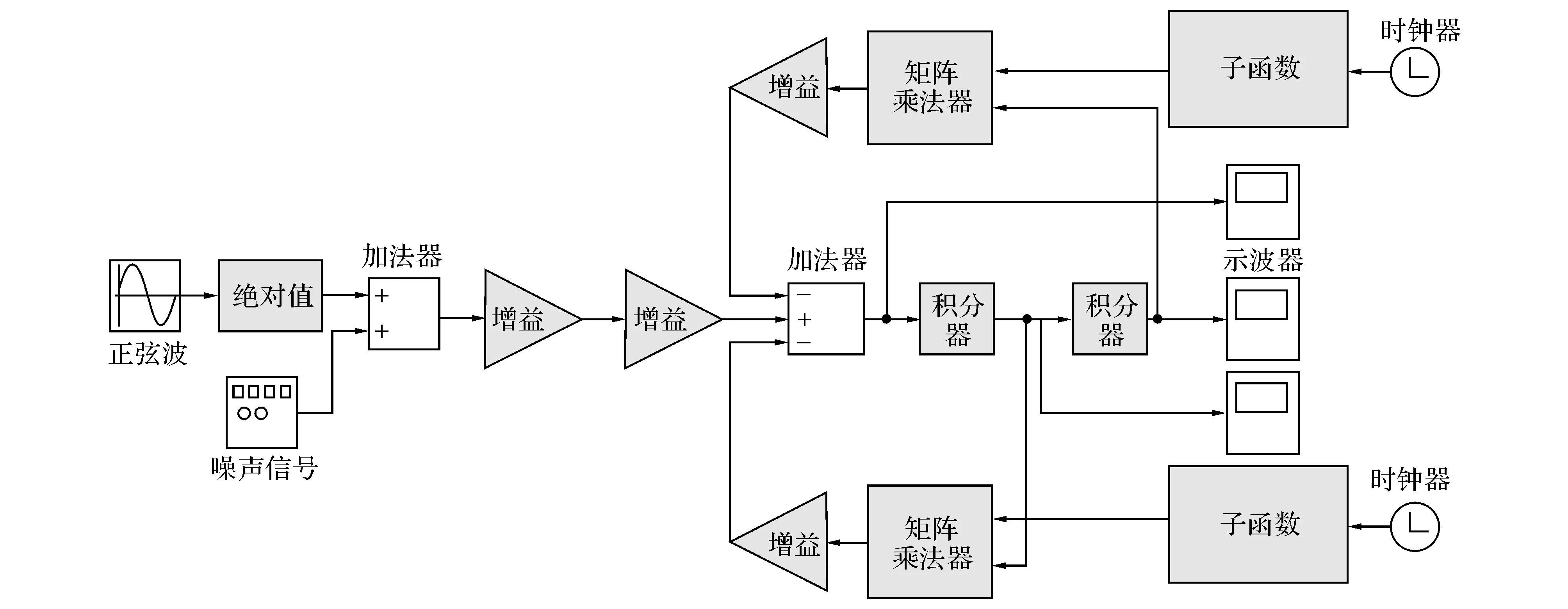
图4　一阶齿轮箱系统的故障仿真模型Fig.4　Fault simulation model of one-stage gearbox system

使用第2章介绍的方法,获得如表3所示的系统故障-征兆矩阵DFS；通过图4所示的故障仿真模型,定性推导各种故障对测试节点的影响关系,进而获得表4所示的征兆-测试矩阵DST.

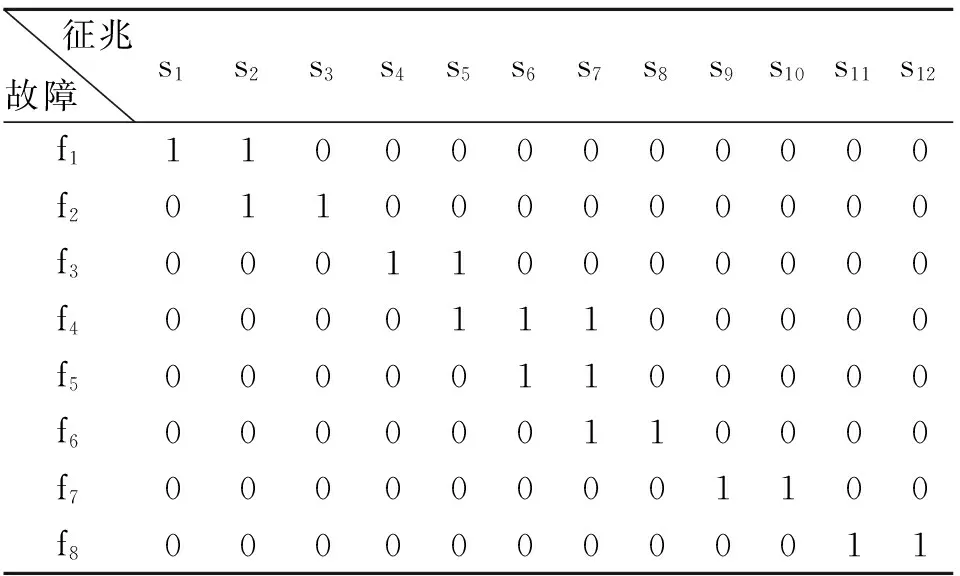
表3　故障-征兆矩阵(DFS)

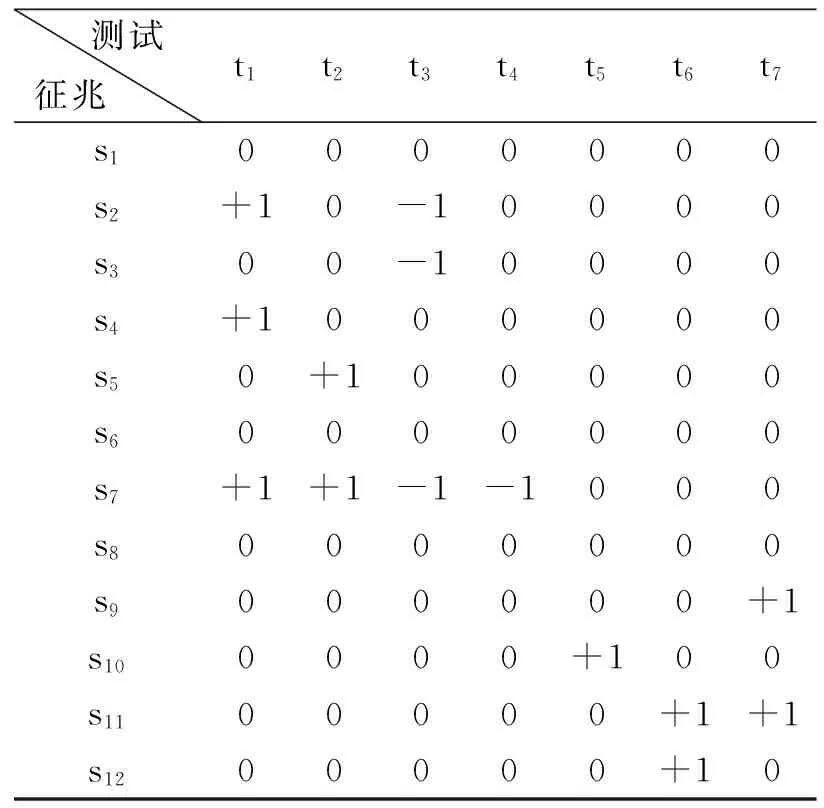
表4　征兆-测试矩阵(DST)

基于以上2个矩阵,使用第3节介绍的测试性预计方法,分析出齿轮箱系统中所有的故障集F={ f1, f2, f3, f4, f5, f6, f7,f8}.如表4所述的矩阵DST,F中每个故障模式至少有一个对应的故障征兆可以被测试节点检测到,因此,可检测的故障集FCD=F={ f1, f2, f3, f4, f5, f6, f7,f8},使用文献[21]介绍的方法计算出故障检测率rfd为100%.如表3所述的故障-征兆矩阵DFS,故障f5的征兆集S(f5)={s6,s7},故障f6的征兆集S(f6)={s7,s8}.在表4中,可以分析出征兆s6和s8构成一个模糊组(对应行相同),显然系统的测试点不能有效隔离这2个征兆参数,进而不能隔离故障f5和f6,因此,不可隔离的故障模式集FUCL={ f5, f6},可隔离的故障集FCL={ f1, f2, f3, f4, f7, f8}.进而根据文献[21]计算出故障隔离率为rfi=98.39%.如表3所述,故障f1的征兆集S(f1)={s1,s2},f5的征兆集S(f5)={s6,s7},f6的征兆集S(f6)={s7,s8}.在表4中,故障f1的征兆s1不能被检测(对应行全为0),可知f1不能被跟踪,故障f5的征兆s6不能被检测(对应行全为0),可知f5不能被跟踪,故障f6的征兆s8不能被检测(对应行全为0),可知f6不能被跟踪,因此,不可跟踪的故障集FUCT={ f1, f5, f6},可跟踪故障集FCT={ f2, f3, f4, f7, f8},根据式(3)计算出故障可跟踪率rft=92.83%；根据以上分析结果,故障f1、f5和f6对应的征兆不能完全被检测,显然也不能隔离,因此,这3个故障不能被预测.同时,由于故障f4的征兆集S(f4)={s5,s6,s7},在征兆-测试矩阵DST中s6和s7都能被检测,但是检测这2个征兆的测试输出值一样(对应行相同).显然,征兆s6和s7都不能被隔离,可知f4不可预测,因此系统中不可预测的故障集FUCP={ f1, f4, f5, f6},可预测的故障集FCP={ f2, f3, f7, f8},根据式(4)计算出故障可预测率rfp=90.66%.详细的测试性预计参数名称和预计指标如表5所示.

表5一阶齿轮箱系统的测试性预计结果

Tab.5Testabilitypredictionresultsofone-stagegearboxsystem

测试性预计参数名称测试性预计指标故障模式总数7故障征兆参数总数12可用的测试集{t1,t2,t3,t4,t5,t6,t7}测试数7FCD{f1,f2,f3,f4,f5,f6,f7,f8}FUCD⌀FCL{f1,f2,f3,f4,f7,f8}FUCL{f5,f6}FCT{f2,f3,f4,f7,f8}FUCT{f1,f5,f6}FCP{f2,f3,f7,f8}FUCP{f1,f4,f5,f6}TR⌀故障可检测率rfd100.00%故障可隔离率rfi98.39.00%故障可跟踪率rft92.83.00%故障可预测率rfp90.66.00%

根据表5列出的测试性预计结果,可以得出如下结论.1)不能隔离的故障集为{ f5, f6},这是由于故障f5和f6的具有相同的征兆s7.同时,这2个故障对应的不同征兆s6和s8对系统中测试节点的影响相同(即对应行相同).因此,如果要有效隔离故障f5和f6,需要在系统中增加测试节点,实现对征兆s6和s8的辨识.2)能跟踪的故障集为{ f1, f5, f6},这是由于故障f1的征兆参数s1不能被测试检测,故障f5的征兆参数s6不能被测试检测,故障f6的征兆参数s8不能被测试检测,因此,如果要有效跟踪故障f1, f5和f6的演化过程,需要在系统中增加测试节点,实现对征兆s1, s6和s8的检测.3)不能预测的故障集为{ f1, f4,f5, f6},由于故障f1的征兆参数s1、故障f4和f5的征兆参数s6以及故障f6的征兆参数s8不能被系统的测试节点隔离.因此,如果要使系统具有预测故障f1、 f4、 f5和f6的能力,需要在系统中增加测试节点,实现对征兆s1、s6和s8的隔离.以上结论可以有效指导设计人员开展测试性设计,以提高齿轮箱系统检测、隔离、跟踪和预测故障的测试性水平.

4结论

本文所提的故障演化测试性建模方法建立了描述部件故障与表征其严重程度的征兆参数之间的关系,能指导设计人员对关键故障模式的演化过程进行监控和跟踪,以实现部件功能失效前提前预警.利用键合图方法从能量流、功能流和材料流3方面建立了系统中故障征兆和测试节点的关系矩阵,能准确描述表征故障增长参数或部件健康参数与测试节点间的关联关系,进而指导设计人员从系统层面布局设置传感器或测试手段实现对系统故障演化过程、健康参数进行有效监控.

本文所提方法还处在理论研究阶段,仅在部分功能结构简单的系统中进行了测试验证,还存在建模周期长、效率低等问题.作者所在科研团队将致力于开发通用的软件工具对本文理论加以实现,以提升工程人员建模的效率,为本文理论在工程中的逐步完善、应用与推广奠定坚实基础.

参考文献(References)：

[1] GURTHY M. Health monitoring, fault diagnosis and failure prognosis techniques for brushless permanent magnet machines [C] ∥VehiclePowerandPropulsionConference(VPPC).Chicago:IEEE, 2011:1-7．

[2] 李丽敏, 王仲生, 姜洪开. 基于多状态MOG-HMM和Viterbi的航空发动机突发故障预测. 振动、测试与诊断[J], 2014,32(4):310-314．

LILi-min,WANGZhong-sheng,JIANGHong-kai.Aero-engineabruptfailureprognosisbasedonmulti-statesMOG-HMMandviterbialgorithm[J].JournalofVibration,MeasurementandDiagnosis, 2014,32(4): 310-314．

[3] 莫固良,汪慧云,李兴旺,等. 飞机健康监测与预测系统的发展及展望[J]. 振动、测试与诊断, 2013,33(6):925-930．MOGu-liang,WANGHui-yun,LIXing-wang,etal.Thefuturedirectionsinitsdevelopmentofhealthmonitoringandprognosisinaircrafts[J].JournalofVibration,MeasurementandDiagnosis, 2013,33(6):925-930．

[4]ORCHARDME,SECANOSGJ.Aparticle-filteringapproachforon-linefaultdiagnosisandfailureprognosis[J].TransactionsoftheInstituteofMeasurementandControl, 2009,31(3):221-246．

[5] 杨丹, 甘春标, 杨世锡,等. 一类初弯曲转子的裂纹-碰摩故障响应分析[J]. 浙江大学学报：工学版, 2014,48(8):1496-1501．

YANGDan,GANChun-biao,YANGShi-xi,etal.Analysisonresponseofarotorwithinitialbenddeformationundercouplingfaultofcrackandrub-impact[J].JournalofZhejiangUniversity:EngineeringScience, 2014,48(8):1496-1501．

[6]CHENACC,BROWNAD,etal.Anintegratedarchitectureforfaultdiagnosisandfailureprognosisofcomplexengineeringsystems[J].ExpertSystemswithApplications,2012,39(10):9031-9040．

[7] 徐玉国. 装备自主维修保障关键技术研究[D]. 长沙：国防科技大学, 2012:1-10．

XUYu-guo.Researchonkeytechnologiesforequipment[D].Changsha:NationalUniversityofDefenseandTechnology, 2012:1-10．

[8]FATIHC,RATNABC.Health-stateestimationandprognosticsinmachiningprocesses[J].IEEETransactiononAutomationScienceEngineering, 2010, 7(2):581-597．

[9]SANTILM,SOWERSTS,AGUILARRB.Optimalsensorselectionforhealthmonitoringsystems[M].NationalAeronauticsandSpaceAdministration:GlennResearchCenter, 2005：1-15．

[10]LVKH,TANXD,LIUGJ,etal.Sensorselectionofhelicoptertransmissionsystemsbasedonphysicalmodelandsensitivityanalysis[J].ChineseJournalofAeronautics, 2014,27(3):643-654．

[11]YANGSM,QIUJ,LIUGJ,etal.Ahierarchicalmodel-basedapproachtotestabilitymodelingandanalysisforPHMofAerospacesystems[J].JournalofAerospaceEngineering, 2014,27(1):131-139．

[12]TANXD,QIUJ,LIUGJ,etal.Faultevolutiontestabilitymodelingandanalysisforcentrifugalpumps[C] ∥PrognosticsandSystemHealthManagementConference(PHM-2014Hunan).ZhangJiajie:IEEE, 2014:469-473．

[13] 吕晓明, 黄考利, 连光耀. 基于多信号流图的分层系统测试性建模与分析[J]. 北京航空航天大学学报,2011,37(9): 1151-1155．

LVXiao-ming,HUANGKao-li,LIANGuang-yao.Modelingandanalyzingfortestabilityofhierarchysystembasedonmulti-signalflowgraphmodel[J].JournalofBeijingUniversityofAerospaceandAstronautics,2011,37(9): 1151-1155．

[14] 丁昊. 基于多信号流图的系统测试性建模分析及软件设计[D], 哈尔滨：哈尔滨工业大学, 2013．

DINGHao.Modeling,analysisandsoftwaredesignforsystemtestabilitybasedonmulti-signalflowgraph[D].Harbin:Harbininstituteoftechnology, 2013．

[15] 石君友. 测试性设计分析与验证[M]. 北京: 国防工业出版社, 2010:21．

[16]CHANGBL,DANWEIW,SHAIA,MINGL.Quantitativehybridbondgraph-basedfaultdetectionandisolation[J].IEEETransactiononAutomationScienceandEngineering, 2010,7(3):558-569．

[17]BORUTZKYW.Bondgraphmodelingandsimulationofmechatronicsystems:anintroductionintothemethodology[C] ∥ 20thEuropeanConferenceonModelingandSimulation2016,Bonn:ECMS, 2006:1-20．

[18] 单晓明, 宋云峰, 黄金泉等. 基于神经网络和模糊逻辑的航空发动机状态监视[J]. 航空动力学报, 2009, 24(10):2356-2361．

CHANXiao-ming,SONGYun-feng,HUANGJin-quanetal.Conditionmonitoringofaero-enginebasedonneuralnetworkandfuzzylogic[J].JournalofAerospacePower, 2009,24(10):2356-2361．

[19]LEBOLDM,MCCLINTICK,CAMBELLR,etal.Reviewofvibrationanalysismethodsforgearboxdiagnosticsandprognostics[C] ∥Proceedingsofthe54thMSMFPT.VirginiaBeach:Springer-Verlag, 2000: 623-624．

[20]BABAKE.Conditionmonitoringofgearboxesusingacousticemission[D].Cranfield:CranfieldUniversity, 2010．

[21]TANXD,QIUJ,LIUGJ,etal.AnovelapproachoftestabilitymodelingandanalysisforPHMsystemsbasedonfailureevolutionmechanism[J].ChineseJournalofAeronautics, 2013,26(3): 766-776．

DOI:10.3785/j.issn.1008-973X.2016.03.007

收稿日期：2015-02-04.

基金项目：国家自然科学基金资助项目(61403408).

作者简介：谭晓栋(1983-)，男，讲师，从事机器状态监控与故障诊断、测试性设计、故障预测与健康管理研究. ORCID：0000-0001-5458-7693. E-mail:xdt1010@126.com.

中图分类号：TP 277

文献标志码：A

文章编号：1008-973X(2016)03-07-0442

Faultevolutiontestabilitymodelingandpredictionformechanicalsystems

TANXiao-dong1,2,LUOJian-lu1,LIQing1,QIUJing2

(1. Department of Electronic Technology, Officers College of PAP, Chengdu 610213, China; 2.Science and Technology on Integrated logistics Support Laboratory, National University of Defense Technology, Changsha 410073, China)

Abstract:A modeling approach based on fault evolution testability model (FETM) was proposed by adopting a multi-level modeling scheme that combined system level and component-level models. The approach adopted a multi-level modeling scheme that combined system-level and component-level models. For component level, the fault evolution mechanism in systems was analyzed, then the qualitative dependency matrix was built to describe the relations between fault and symptom parameters. For system level, bond graph methodology was used to model the relations of energy transfer among faults that occurred in components, the parameters of subsystems and systems, thus the dynamic relations between symptom parameters and tests could be obtained. On the basis of fault detection rate and fault isolation rate, fault tracking rate and fault prediction rate were developed to describe the testability of detecting, isolating, tracking and predicting failures, respectively. The results of the case study show that the relations between fault evolution and tests can be described correctly by the qualitative relations between faults and symptom parameters, and the dynamic relations between symptom parameters and the tests of systems. According to those relations, the testability prediction can be utilized to evaluate the systems’ capabilities of detecting, isolating, tracking and predicting failures. And the prediction results contribute to improve the ability of mechanical systems of tracking fault evolution process and predicting fault．

Key words:testability modeling and prediction; design for testability；fault-test dependency; bond graph