防灾避难场所选址优化模型

陈红月，初建宇，2，马丹祥，2，孙天威

（1．华北理工大学建筑工程学院，河北唐山063009；2．河北省地震工程中心，河北唐山063009）

防灾避难场所选址优化模型

陈红月1，初建宇1，2，马丹祥1，2，孙天威1

（1．华北理工大学建筑工程学院，河北唐山063009；2．河北省地震工程中心，河北唐山063009）

避难场所；选址优化；责任区分配；综合集成赋权；双层规划

为解决避难场所选址与责任区分配问题，综合政府和避难人员对避难场所选址的要求，建立双层规划选址优化模型。模型指标权重的确定采用序关系法和熵值法综合集成赋权，利用LINGO软件对模型求解。结果表明该模型顾整体与局部，相比多目标规划模型更能反应规划的实际情况。

0 引言

防灾避难场所（简称避难场所）是指定用于因灾害产生的避难人员集中进行救援和避难生活，配置应急保障基础设施和应急辅助设施的避难场地及避难建筑［1］。避难场所选址不仅关系到其灾后能否发挥应急救援的功能，更关系到避难人员的生命安全。2008年汶川地震后，多个避难场所被暴雨造成的泥石流损毁或掩埋，造成多人伤亡或失踪［2］。2011年东日本地震后，大量疏散到避难场所中的民众受到海啸伤害［2］。2008年汶川地震后，绵阳九州体育馆被设置为避难场所，由于未考虑服务责任区，导致其接受的避难人员远远超过最大容量，民众的避难生活受到很大影响。避难场所合理选址与责任区分配至关重要，有利于提高城乡对灾害的防御能力，保证居民安全避难和有序避难。

目前，国内外对避难场所选址有一定研究成果。Luis Alcada－Almeida等［3］建立了火灾避难场所的布局多目标优化模型；Joao等［4］从总疏散距离最小、通过备用路径的疏散距离最少和场所总个数最小三方面考虑，建立多目标优化模型；Kongsomsaksakul［5］从规划部门和疏散人员的不同角度，建立距离最短，数量最少的双层规划模型；吴健宏等［6］依据总疏散距离最小，避难场所利用率最大，避难场所数量最小，构建了多目标优化模型；刘少丽［7］依据设施区位模型及其算法构建了避难场所空间布局优化模型；马丹祥等［8］考虑总疏散距离最小和避难场所适宜性最好，建立了多目标规划模型。现有研究中，避难场所规划目标是数量少、距离短，很少有对避难场所自身适宜性和避难人员的需求综合考虑的，无法体现政府和避难人员的实际需求，影响了模型的实用性。

避难场所选址规划应综合考虑政府与居民的需求，二者的决策有先后之分，但又互相影响。政府在选择避难场所时，主要考虑避难场所的数量与其自身的适宜性，在满足规定的服务范围内，使居民在数量最少和适宜性最好的场所进行避难；而避难人员在政府指定的避难场所中，往往倾向于选择场所较大、距离较近的避难场所，以获得较好的服务和减少疏散时间。根据上述实际情况，建立了避难场所选址和责任区分配的双层规划模型，并给出求解方法。

1 避难场所选址指标

借鉴文献［7］中对避难场所提出的评价指标，具体见表1。

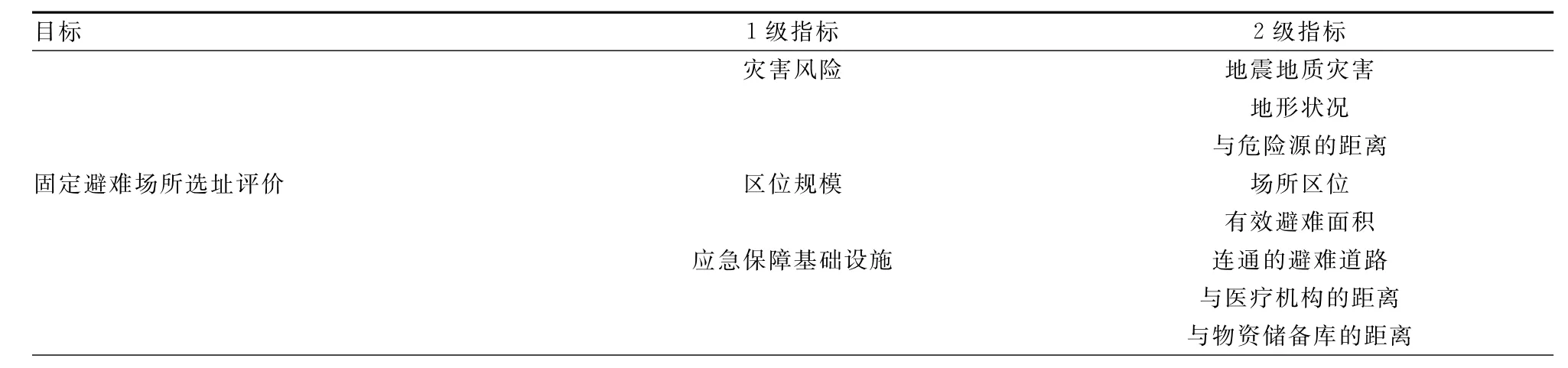
表1 选址评价指标体系

评价指标权重的确定方法，采取序关系法和熵值法的综合集成赋权方法。J为备选避难场所集合；K为政府决策时对避难场所适宜性起决定作用的影响因素集合

步骤1：依据序关系法进行赋权，首先请专家依据上述指标进行重要性排序，得出指标集合记为K＊＝，依据rk＊＝wk＊－1／wk＊（k＊＝2，3，…，t），具体赋值见表2得出专家对k＊－1指标与k＊指标重要程度的比值，依据公式（1）、（2）求出权重。

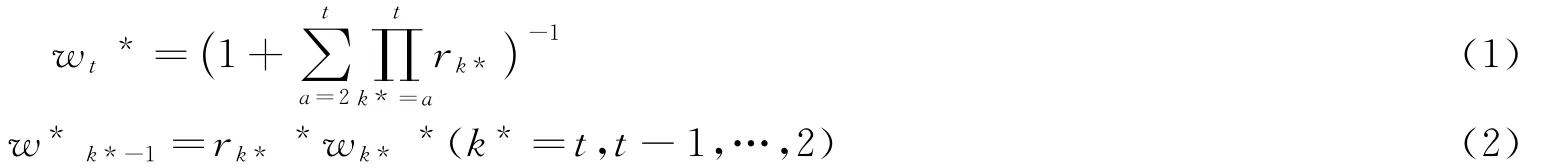
设邀请c个专家进行指标排序，若有c0个专家排序相同，则依据公式（1）、（2）求出权重w＊k＊，剩下不同排序的专家，依据公式（3）求出权重w＊＊k＊，最后对应w＊k＊和w＊＊k＊，按表1中指标顺序排序，记为w＊k和w＊＊k，依据公式（4）求出权重w＇k。

wlk＊表示第l个专家对第k＊个指标的权重，由公式（1）、（2）求解；k1和k2分别为wk＊和wk＊＊系数，k1＝c0／ck2＝（c－c0）／c。

表2 数值说明表

步骤2：依据熵值法进行赋权，首先对不同型指标依据公式（5）、（6）进行规范化处理，再依据公式（7）求取指标的熵值hk；公式（8）求出权重w＇k。

式（7）中

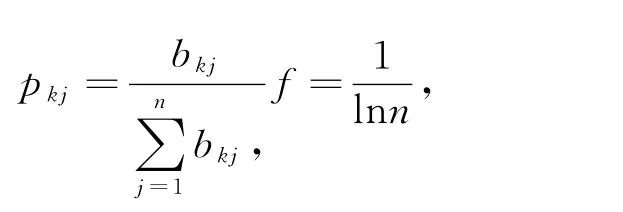
当pkj＝0时，规定pkjln（pkj）＝0

步骤3：依据综合集成赋权法进行赋权，为了同时体现主管权重和客观权重，最终向量为，已知方案J在适应性因素K的影响数值为bkj，则主观加权属性值为，同理客观加权属性值为，二者差异为，因此可以确定方案J的主观权重值得偏离程度为dj＝若要确保主客观权重的一致性，则应确保二者的偏离程度最小，依据公式（9）、（10）、（11）优化权重。

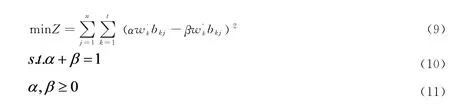
2 建立选址与责任区分配的双层规划模型

首先双层规划模型中的上层决策机构为政府，主要是考虑成本、时间因素从备选避难场所中选择适宜的避难场所，即选择最少数量的避难场所，而且这些场所的适宜性最好；下层决策机构为避难人员，依据政府规划的避难场所，综合考虑与避难场所的距离和避难场所容量，选择距离短、容量大的避难场所避难。

2．1 基本假设

（1）所有需求区和备选避难场所的位置是确定和离散的；

（2）住宅区、商业区、工业区等需求区到备选避难场所的距离均为出入口之间的最短路网距离；（3）每个需求区的人口数量和每个备选避难场所的避难容量均为已知的；

（4）每个选中的避难场所中容纳的避难人数不能超过该场所的最大避难容量；

（5）任何一个避难需求区的全部避难人员全在且只在一处避难场所进行避难；

（6）每个避难场所中所有避难人员对避难场所的考虑因素一致。

2．2 模型参数

优化选址模型为求得数量最少，适宜性最好并且最符合避难人员需求的避难场所，上层模型与下层模型均是求解最小值，上述参数在进行规范化处理时，需要分别依据成本型指标和收益型指标的分类对应转化为最小为最佳的数值。其中成本型指标规范化公式为（5），效益型指标规范化公式为（6）。

2．3 避难场所选址优化模型

上层模型：

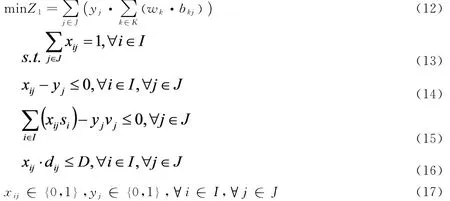
目标函数式（12）表示选择的避难场所适宜性评价值；公式（13）确保每个需求区均在一处避难场所避难；公式（14）确保每个需求区只在选中的避难场所避难；公式（15）确保被选中避难场所接受的避难人数不超过该场所容量；公式（16）确保每个需求区到其选中的避难场所的距离满足标准要求最大疏散距离D；公式（17）为变量的限制条件。

下层模型：

目标函数式（18）表示保证所有人总疏散距离最短并且所选避难场所越大越好；公式（19）确保每个需求区均在一处避难场所避难；公式（20）确保每个需求区只在选中的避难场所避难；公式（21）表示群众只在范围D内挑选最佳避难场所；公式（22）为变量的限制条件。

3 算例分析

以某市河东片区固定避难场所选址优化为研究对象，利用该项研究中提出的选址优化模型，进行避难场所选址与责任区分配。其中各个备选避难场所的指标数据如表3所示，需求区与备选避难场所距离等其他数据如表4所示。

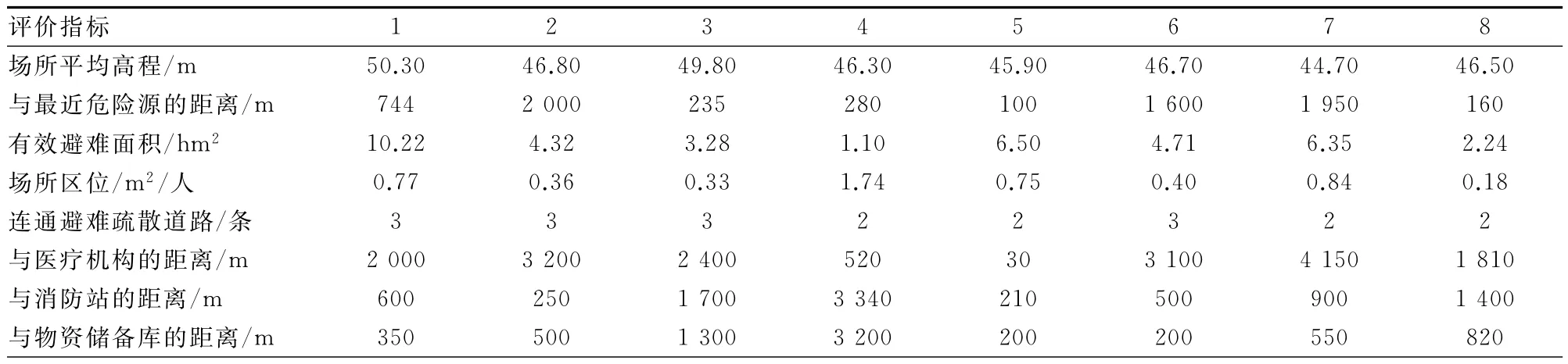
表3 备选避难场所指标原始数据

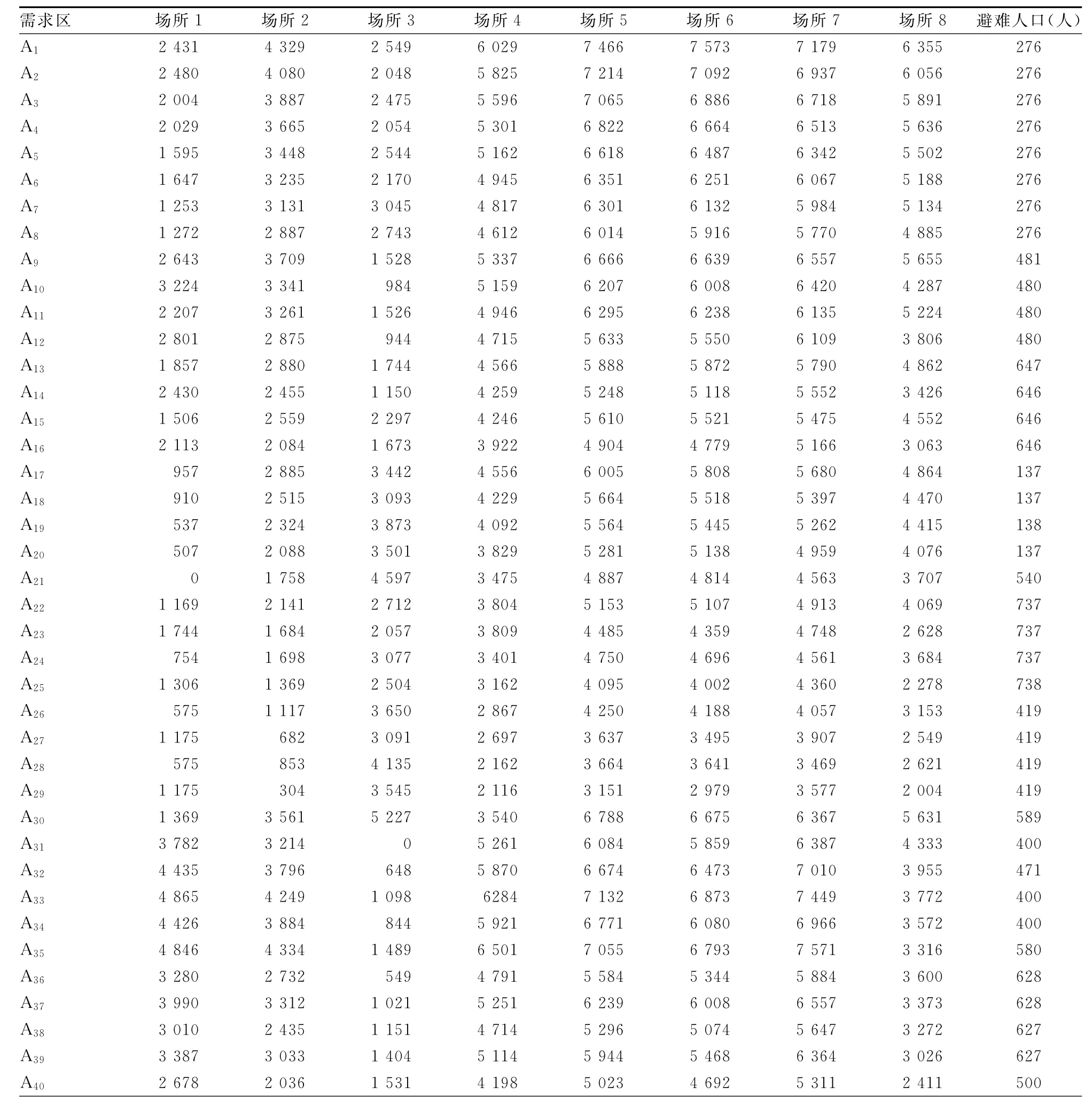
表4 避难需求区人口及与备选避难场所的距离数据

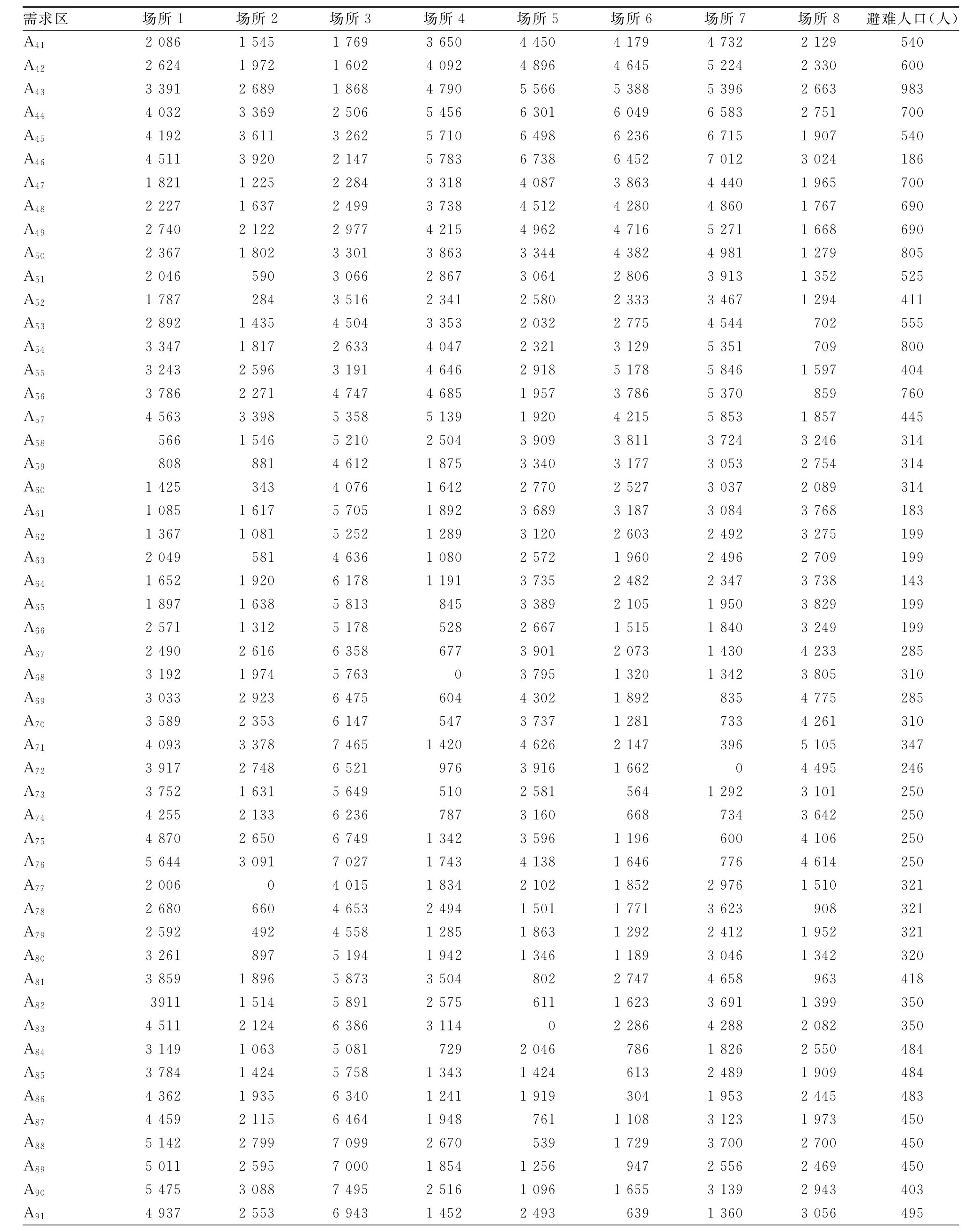
表4续：

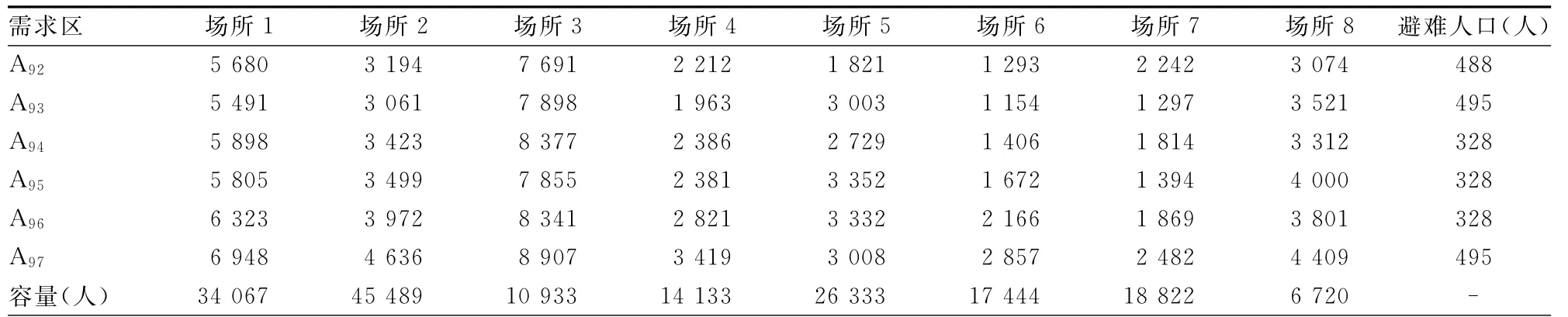
表4续：

首先对指标权重进行计算，参照专家的意见，依据群组序关系法计算出上述评价指标的权重为（0．195，0．230 6，0．124 5，0．104 5，0．087，0．102，0．068 9，0．087 5）；依据熵值法计算出上述评价指标的权重为（0．069 9，0．1，0．052 5，0．122 7，0．202，0．072 7，0．161 6，0．218 6）；再依据综合赋权法可得指标权重为（0．126 9，0．159 6，0．085 3，0．114 4，0．149 6，0．086，0．119 3，0．158 8）。在此例中取D＝3 000m，下层避难人员选择场所时距离与场所容量的权重依据文献［10］中调查数据，距离权重取0．39，避难场所容量权重取0．61。本文利用LINGO11．0软件求取避难场所选址分配情况，求解结果如表5所见。

表5 求解结果

4 结论

为解决避难场所选址和责任区分配问题，建立了双层规划模型，其中，上层规划模型从政府角度考虑，以避难场所数量少、适宜性好为目标，下层规划模型从避难人员角度考虑，以疏散距离短、避难场所规模大为目标。该双层规划模型顾整体与局部，使避难场所选址布局达到最优，相比多目标规划模型，更具有层次性，更能反应规划过程中的实际情况。

［1］ 河北省地震工程研究中心．GB51143－2015，防灾避难场所设计规范［S］．北京：中国建筑工业出版社，2016．

［2］ 宋晓勇．汶川地震灾区安置点的防灾研究［J］．消防科学与技术，2010，29（12）：1058－1064．

［3］ Luis Alcada－Almeida，Lino Tralhao，Luis Santos，ect．A Multiobjective Approach to Locate Emergency Shelters and Identify Evacuation Routes in Urban Areas［J］．Geographical Analysis，2009，41：9－29．

［4］ Joao Coutinho－Rodrigues，Lino Tralho，Luís Alda－Almeida．Solving a Location－routing Problem with a Multiobjective Approach：the De－sign of Urban Evacuation Plans［J］．Journal of Transport Geography，2012，22：206－218．

［5］ Kongsomsaksakul S，Chen A，and Yang C．Shelter Location－allocation Model for Flood Evacuation Planning［J］．Journal of the Eastern Asia Society for Transportation Studies，2005，（6）：4237－4252．

［6］ 吴健宏，翁文国．应急避难场所的选址决策支持系统［J］．清华大学学报（自然科学版），2011，51（5）：632－636．

［7］ 刘少丽．城市应急避难场所区位选择与空间布局－－以南京市为例［D］．南京：南京师范大学，2012．

［8］ 初建宇，马丹祥，苏幼坡．基于理想点的已知部分属性权重信息中心避难场所选址方法研究［J］．自然灾害学报，2012，21（4）：28－32．

［9］ 初建宇，马丹祥，苏幼坡．基于组合赋权TOPSIS模型的城镇固定避难场所选址方法研究［J］．土木工程学报，2013，46（2）：307－312．

［10］ 郭积杰，郭晓明，王宝刚．四川震灾地区乡镇防灾规划建设调查报告［J］．小城镇建设，2009，（8）：71－73．

Location Selection of Emergency Shelter Optimization Model for Disaster Prevention

CHEN Hong－yue1，CHU Jian－yu1，2，MA Dan－xiang1，2，SUN Tian－wei1
（1．College of Civil and Architectural Engineering，North China University of Science and Technology，Tangshan Hebei 063009，China；2．Earthquake Engineering Research Center of Hebei Province，Tangshan Hebei 063009，China）

emergency shelter；location optimization；distribution of the responsibility area；integrated empowerment；bi－level programming

To solve the problem of location selection of emergency shelter and area distribution，synthesizing administration and personnel requirements for the location of the shelter，a bi－level programming optimization model for site selection was established．Using sequence relations and entropy value method comprehensive integration，the target weights of the model was determined and by using the LINGO software，the model was solved．The results show that the model focuses on the whole and local，and compared with the multi－objective programming model can response planning more actual situation．

X43

A

2095－2716（2016）04－0149－08

2016－05－23

2016－09－27

国家科技支撑计划（2013BAJ10B09－2）。