十字形截面钢管混凝土异形柱正截面承载力全过程分析

陈海彬，周凤勤，葛楠

（华北理工大学河北省地震工程研究中心，河北唐山063009）

十字形截面钢管混凝土异形柱正截面承载力全过程分析

陈海彬，周凤勤，葛楠

（华北理工大学河北省地震工程研究中心，河北唐山063009）

十字形截面；钢管混凝土；异形柱；全过程分析

根据钢筋混凝土梁理论，给出了十字形截面钢管混凝土异形柱正截面承载力的计算方法。根据平截面假定建立了十字形钢管混凝土异形柱截面弯矩－曲率关系计算公式，并利用MATLAB语言编制了求解程序，通过得到的加载－破坏全过程弯矩－曲率关系分析构件的加载－变形特性。对求得的弯矩－曲率的关系和矩形截面进行比较和分析，同时给出不同混凝土标号、钢材强度、钢管面积下的十字形截面异形柱截面的弯矩－曲率。

0 引言

异形柱框架结构房屋使用功能好，造价较低，可用于高层建筑，节约用地。但其抗震性能是目前需要迫切解决的问题。根据异形柱截面肢长较长的特点，采用带钢管边框的异形柱可以解决其抗震性能问题，例如延性特性、耗能特性等。虽然具备了构造上的特点，但是其整体结构的抗震性能也需要根据实际的震害或结构地震反应分析来评定。在采用有限元方法进行地震反应分析时，对于建筑工程中常见的结构形式，往往由数量众多的构件组成，采用3D实体单元对整个结构建模分析几乎是不可能的，需要采用传统的杆系单元建模，通常用梁单元模拟梁、柱等构件，用带刚域的梁单元模拟剪力墙和连梁。

用桁架单元模拟支撑。

目前在采用杆系有限元方法分析结构的地震反映时，还不能准确地模拟混凝土材料与钢筋材料的非线范围的卸载－再加载特性，因此结合结构静力推覆分析（push－over analysis，实际是结构单向加载直至破坏的全过程）结果可以更准确地评价结构的抗震性能，这时应用钢筋混凝土梁的弯矩－曲率曲线能较准确地反应混凝土梁截面变形、开裂、屈服、破坏的全部过程，因此也能反应整体结构的变形过程，据此从整体结构的层次上评价结构的抗震性能。2005年，陈宗平等［1］依据型钢混凝土异形柱的破坏原理，对其正截面承载力进行有限元分析，将型钢和混凝土进行单元划分，应用不同的坐标系进行处理，利用数值迭代方法编写计算机程序分析截面的变化规律。2009年，杜宏彪等［2］应用结构有限元对一钢筋混凝土异形柱框架结构进行Pushover分析。2011年，陈惠满等［3］应用平截面假设和钢管混凝土的本构关系对异形柱钢管混凝土柱正截面承载力进行计算和分析，通过截面混凝土和钢管的割线刚度矩阵和截面应变平面的积求得截面承载力。这种计算方法对截面破坏过程分析不够直观。2015年，李凯文等［4］通过试验对型钢高性能混凝土十字形异形柱试件的各阶段开裂变形及破坏形态进行观测并分析破坏机理。本文根据钢筋混凝土梁理论以及简化模型，推导出了十字形异形柱截面弯矩－曲率曲线迭代计算公式，并利用Matlab软件编制了求解程序，在结构推覆分析中可以采用。

1 截面弯矩曲率曲线的意义

对于钢筋混凝土梁单元，由于通常已经进入非线性阶段，因此其截面抗弯刚度与由材料力学求得的弹性范围内截面抗弯刚度EI是有区别的，需要根据混凝土及钢筋材料的应力应变关系特性以及截面上裂缝的发展变化过程建立截面抗弯刚度的计算公式。

如图1所示，一个钢筋混凝土梁单元，长度为l，单元节点力与节点位移分别为［Fe］及［Δe］

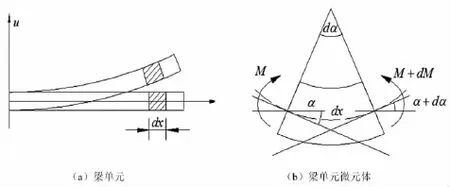
图1 梁单元及微元体示意图

在梁单元中取一个微元体dx，其位移为u（x）。在受力变形后，其截面仍然符合平截面假定［5］。假设在加载到某一子步时其弯曲变形转角为da，则根据截面抗弯刚度K与截面弯矩M及变形曲率（da／dx）之间的关系，有：

即

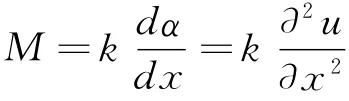
设

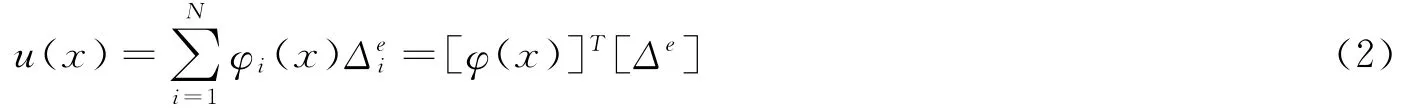
其中［φ（x）］是位移插值函数，［Δe］是节点位移，则

当节点发生虚位移［δΔe］时，梁单元x处的虚位移为：

根据虚功原理，有：外力虚功等于内力虚功，即：

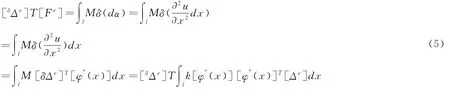
因此，有：

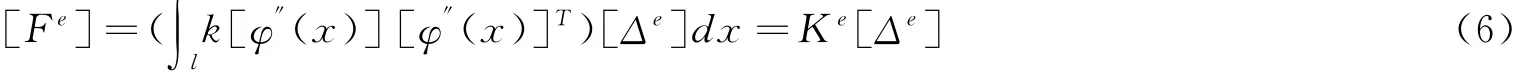
当梁单元进入非线性状态时，在单元刚度矩阵中，k随荷载而变化。从（1）中可知，任意截面的k可以由以下公式计算：

φ为x处截面的曲率。另一方面，在梁单元的长度范围内，k沿长度也是变化的，在确定Ke时也需要已知k沿梁单元的长度分布函数，目前有3种方法：平均刚度法，分布刚度法，集中塑性铰刚度法［6］。

对于任意一个截面，则必须根据荷载施加过程，在每一个荷载子步下，按照（8）式逐步求出k，M／φ既是截面的弯矩－曲率关系。对于钢筋混凝土构件，需要按照截面分析法确定M与φ的关系曲线。

2 计算模型

十字形钢筋混凝土异形柱的截面如图2（a）所示。

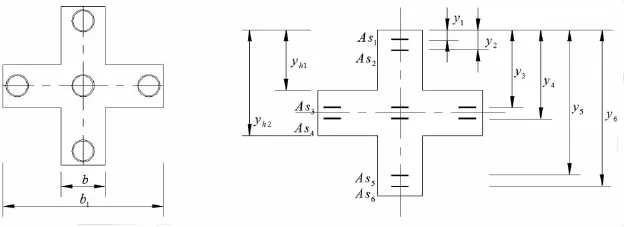
图2 十字形钢筋混凝土异形柱截面

由于计算钢管截面的应力比较复杂，为了能够简化计算，对钢管截面进行简化，将钢管平均等分成两部分，每部分简化成等面积的钢筋，半圆环的重心位置为钢筋的作用位置。几何模型如图2（b）所示。

钢筋本构关系应用双直线型的应力与应变关系的曲线，不考虑钢筋的强化段。应力应变关系表达式为：

当εs＜εy时，σs＝Esεs

当εs≥εy时，σs＝fy

其中，

εs，σs——钢筋的应变和应力；

εy，fy——钢筋的屈服应变和屈服应力；

Es——钢筋初始的弹性模量。

压区混凝土采用的本构模型的关系公式为：

当εc≤ε0时，σc＝fc［1－（1－εc／ε0）2］

当ε0＜εc≤εu时，σc＝fc

其中，

εc，σc——混凝土的应变和应力；

fc——混凝土的峰值应力；

ε0——混凝土峰值应力对应的应变，取ε0＝0．002；

εu——混凝土的极限压应变，取εu＝0．003 5。

3 截面弯矩曲率关系确定

3．1 各特征点应变计算

当构件受力后，混凝土发生塑性变形，随着受拉区混凝土裂缝的出现，混凝土的应变逐渐增大。中和轴位置向下移，受压区高度不断变大。计算受压受压应变时，有ε＝（1－y／x）εct，计算受拉应变时，有ε＝（y／x－1）εct，其中x是截面受压区高度，y可以是任意特征点对截面上边缘的坐标值，相应的截面曲率计算公式为φ＝εct／x。

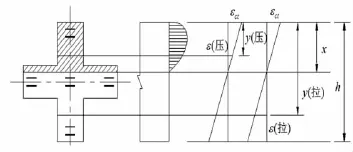
图3 截面各点应变计算示意图

3．2 方程的建立及求解

取轴向力平衡和对受拉的钢筋y6取力矩平衡，公式为∑X＝0及∑M＝0，但是当截面中和轴位置不同时，计算公式有差别，例如当y2＜x≤yh1时，上述2个方程的形式如下：

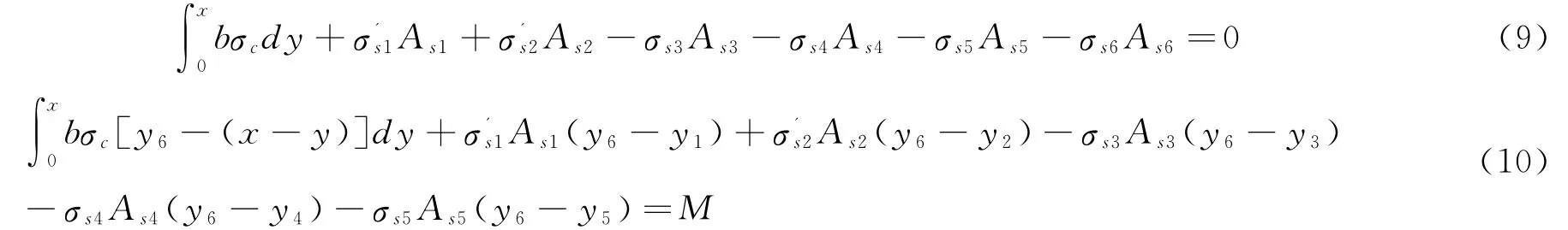
将As1，As2，As3，As4各点及混凝土的应变－应力代入到以上两个平衡方程中，方程中只含有εct和x2个未知的变量，通过2个方程可以求解，然后得到弯矩和曲率的值，注意在（9）式中，有dy＝－（x／εct）dε，与参考文献［7］中的表示法有区别。由于材料的非线性的本构关系和裂缝的不断开展，上述的平衡方程很难求出解析解，因此需要编制计算机程序，利用计算机来实现截面的全过程分析。

可先假定曲率已知，根据公式φ＝εct／x，可知每一个εct对应一个x，编制软件时实际求解方法，关键是在于已知εct求出截面受压区高度x。求解的步骤如下：

（1）开始计算：假定εct起始值为0，则x的起始值也为0；

（2）使εct每次增加0．000 05，这时需求出相应的受压区高度x；

（3）取第1个受压区高度x1为上一个εct的受压区高度，这时截面合力可能不为0，存在余量N1；

（4）取受压区高度x2为任意值，这时截面合力不为0，存在余量N2；

（5）根据x1－N1和x2－N2之间的关系，取线性内插或外延计算N＝0对，取第3个受压区高度x3为：

使x3对应的截面合力余量N3接近于0；

（6）取受压高度x2为x3（或任意值），这时截面的合力仍然可能不为0，存在余量N3，则再重复（5）～（6）步，使截面合力余量N＝N3接近于0的误差满足要求，即求出与εct相应的x＝x3；

（7）计算截面弯矩值，并且重复（2）～（6）得到一系列的εct／x－M，即得到的弯矩曲率曲线。可以利用Matlab语言编制求解程序。

4 截面尺寸及计算结果分析

4．1 截面尺寸

图4和图5所示分别为矩形截面和十字形截面尺寸，其中的钢管内径为92mm，外径为102mm。用Matlab编写的求解程序对这2个截面进行求解，得到截面弯矩和曲率的关系曲线。并对这2个曲线进行分析。通过编写的求解程序对不同混凝土标号、钢材强度、钢管面积下的十字形截面弯矩和曲率的关系进行求解。

4．2 计算结果及分析

图6所示为十字形截面弯矩和曲率关系曲线图。

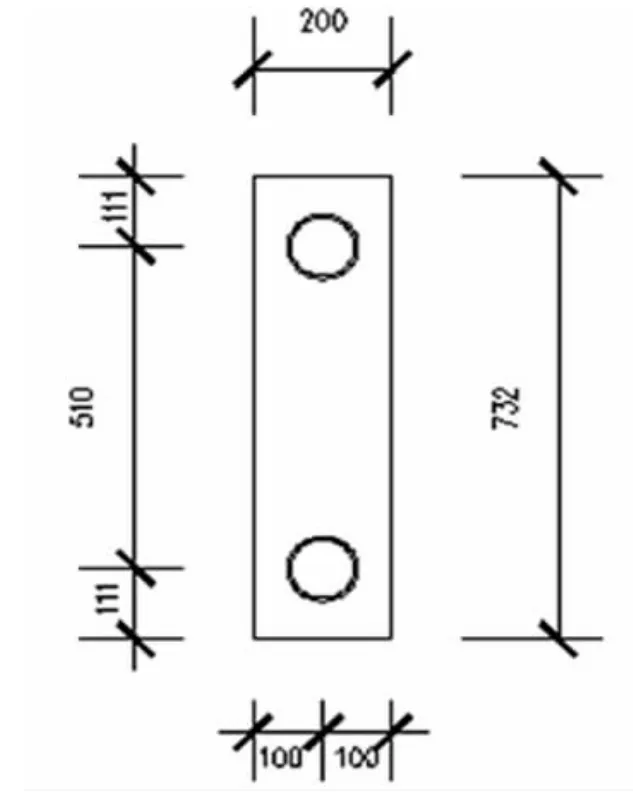
图4 矩形截面尺寸

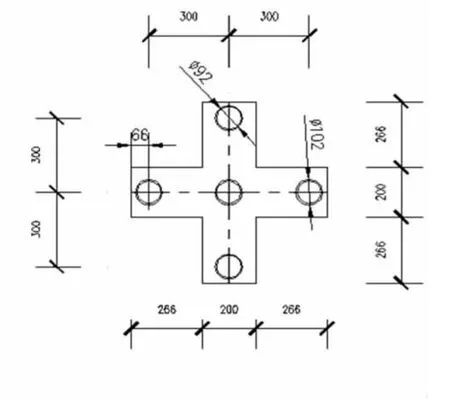
图5 十字形截面尺寸

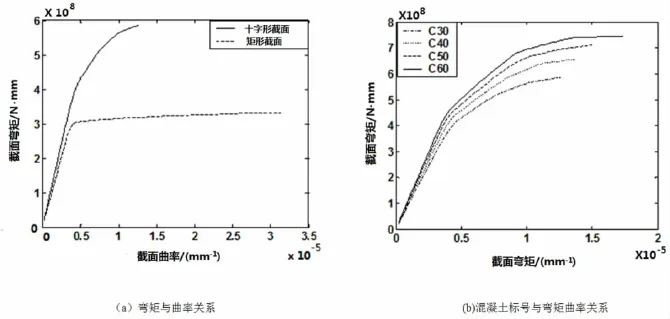
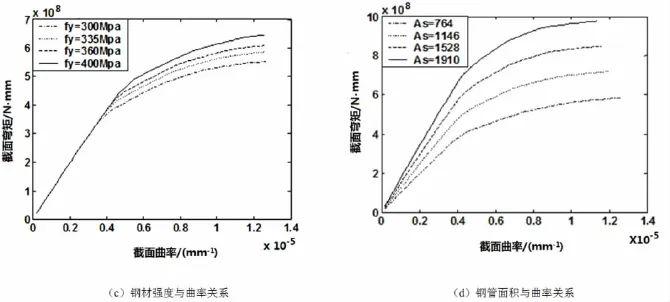
图6 十字形截面弯矩和曲率关系曲线图

截面弯矩－曲率关系曲线可以反映出随荷载增加，构件变形－破坏过程的特点。从图6（a）可以看出，十字形截面异形柱（5根钢管）比矩形截面（2根钢管）的极限弯矩值大幅提高，约提高1倍左右，但是极限曲率值也减小了50%以上。由于受到十字形截面形状的限制，在截面的中部布置了3根钢管。而在截面的边缘只能各布置1根钢管，同时为了构造上的要求中部的钢管不能减少，对受弯构件来说降低了钢管的使用效率，但十字形截面柱一般为中柱，按照“强柱弱梁”的规定，在承受水平地震的作用时，柱端塑性铰要出现在梁端塑性铰之后，塑性铰的转角也较小，因此极限曲率降低对中柱抗震性能影响小，而极限弯矩提高对满足“强柱弱梁”的规定更为有利，这也符合“当承载力满足要求时，不必苛求延性”的性能设计的思想。从图6（b）中可以看出，随着混凝土标号的提高，极限弯矩也随之提高，但从C25－C60的变化中，极限弯矩值提高较小，极限曲率也有一定幅度的提高，这是因为随着混凝土标号的提高，达到极限破坏状态（受压区边缘混凝土压应变达到极限值）时的截面受压区高度变小了，使得截面曲率增大。从图6（c）中可以看出当钢筋屈服强度提高时，极限弯矩也随之提高但提高的幅度不明显。因此提高混凝土标号或采用高强钢材对提高抵抗水平地震的能力效果有限。从图6（d）中可以看出，增加钢管截面面积时，极限弯矩也随之提高，由于增加钢管面积在构造上容易实施，因此若增加钢管面积的数量较多，则可以明显地提高极限弯矩－即提高抵抗大震的能力，此时极限曲率值略有降低，但是在异形柱框架结构中，柱子不属于耗能构件，需要满足强柱弱梁的要求，当截面极限弯矩值较高时，不出现塑性铰是理想的状态，因此可以采用较大的钢管面积。

5 结论

（1）根据钢筋混凝土梁原理利用平截面假定得到十字形截面钢管混凝土异形柱正截面弯矩－曲率的计算公式，并利用MATLAB编制了求解程序。

（2）十字形截面异形柱（5根钢管）比矩形截面（2根钢管）的极限弯矩值大幅提高，约提高1倍左右，但是极限曲率值也减小了50%以上。

（3）提高混凝土标号或钢管的屈服强度等级对提高极限弯矩的效果均不明显，但增加钢管截面面积对提高极限弯矩具有明显的效果，极限曲率仅略有降低。

参考文献：

［1］ 陈宗平，张喜德，苏益声，等．型钢混凝土异形柱正截面承载力的理论研究［J］．2005，37（3）：346－355．

［2］ 杜宏彪，管民生．钢筋混凝土异形柱框架结构Pushover分析［J］．工程抗震与加固改造，2009，31（4）：13－18．

［3］ 陈惠满，陈颖，焦俊婷．异形钢管混凝土柱截面承载力计算［J］．厦门理工学院学报，2011，19（1）：62－65．

［4］ 李凯文，刘国华，万鑫，等．型钢高性能混凝土十字形异形柱抗震性能试验研究［J］．工程抗震与加固改造，2015，37（6）：8－14．

［5］ 过镇海，王传志．钢筋混凝土原理［M］．北京：清华大学出版社，2005．

［6］ 江见鲸，陆新征，叶列平．混凝土结构有限元分析［M］．北京：清华大学出版社，2005．

［7］ 曹素卿，王兴国．框架梁柱正截面受力性能的全过程分析［J］．河北理工大学学报，2007，29（3）：120－122．

Full－Range Analysis of Normal Section Bearing Capacity for Crisscross Section Concrete－Filled Circular Tubular Special－shaped Column

CHEN Hai－bin，ZHOU Feng－qin，GE Nan
（Earthquake Engineering Research Center of Hebei Province，North China University of Science and Technology，Tangshan Hebei 063009，China）

crisscross section；concrete－filled circular tubular；special－shaped column；full－range analysis

According to the theory of reinforced concrete beams，the calculation method of the normal section bearing capacity of concrete－filled circular tubular special－shaped column with crisscross sections is presented．Based on the plane section assumption，a calculation formula of moment－curvature curve for crisscross section concrete－filled circular tubular special－shaped column is established．Meanwhile，solving program is made by using MATLAB．Through using the moment－curvature formula of loading－failure whole process，loading－deformation characteristics of special－shaped column are analyzed．Furthermore，the moment－curvature curve of crisscross section and rectangular cross section are compared，and the crisscross section moment－curvature curves of different concrete grade，different steel stiffness，different steel area are given．

TU375．4

A

2095－2716（2016）04－0118－07

2016－04－25

2016－09－20

国家自然科学基金项目（51478162，51378170），河北省重点基础研究项目的资助。