一类特殊反对角方程组的追赶法及其实现
吴宇航,阎少宏,彭美叶
(华北理工大学理学院,河北唐山063009)
一类特殊反对角方程组的追赶法及其实现
吴宇航,阎少宏,彭美叶
(华北理工大学理学院,河北唐山063009)
反三对角方程组;非奇异矩阵;YH分解;追赶法
研究了反三对角方程组的求解问题。首先给出了反三对角矩阵A的定义,其次证明了满足严格反对角占优的反三角矩阵为非奇异矩阵,然后通过利用YH矩阵分解的方法,推导得出了反三对角方程组的追赶法,最后运用算例进行演示。
0 引言
随着现代工业和科学技术的发展,线性方程组的应用出现在经济管理、工程计算等各个领域,许多应用会导出一些具有特殊结构的稀疏线性方程组的计算问题[1,2]。伴随着这些方程组的出现,寻找简便而且准确的求解方法就显得十分重要而且具有现实意义。
反三对角方程组是反对角方程组中比较常见的一类,在力学、流体力学、工程学等领域有很重要的应用。事实上,因为许多实际问题通常会采用微分方程模型来描述,然后用有限元方法、差分方法等来求其数值解,这类问题的最终解决又归结为解大型线性方程组的问题。在对角线性方程组的解法中,追赶法因其计算公式简单,运算量和存储量小,在科学领域中被广泛运用。因此,在借鉴文献[3-6]的思想后,建立求解反三对角方程组的追赶法,然后算例进行演示。
1 预备知识
定义1若方阵A=(aij)的元素当1≤i≤n-2,1≤j≤n-i-1且3≤i≤n,n-i+3≤j≤n时,均有aij=0,则称此矩阵为反三对角矩阵。
定义2若反三对角矩阵A满足条件(1),则A为严格反对角占优矩阵。
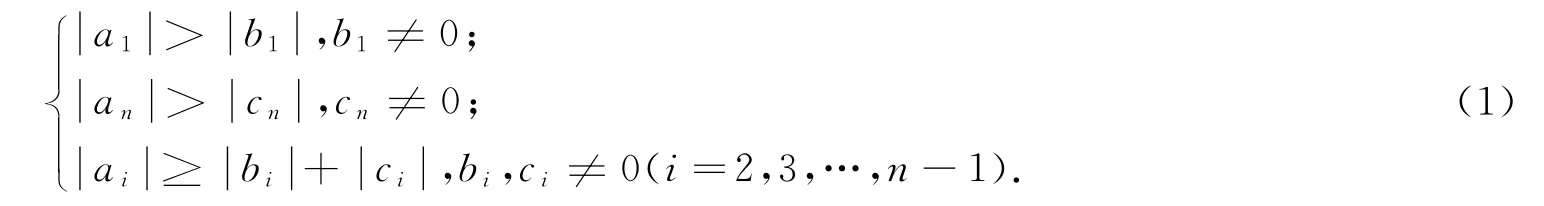
引理1对于任意阶数不小于2的反三对角矩阵A,一般记:

若满足条件(1),则矩阵A为非奇异矩阵。
证明:利用行列式初等变换把矩阵A转化成三对角矩阵。即,
当n=4wn=4w+1(w为任意大于零的整数)时,

当n=4w+2n=4w+3(w为任意大于零的整数)时,
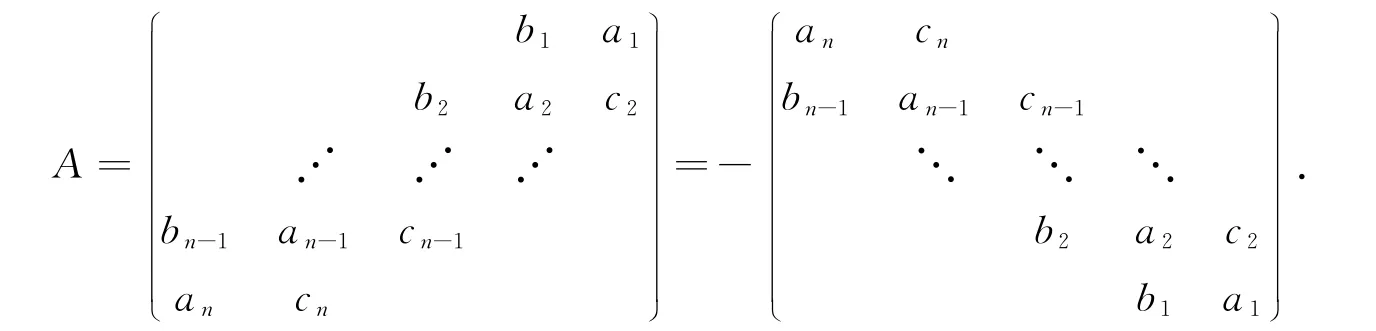
通过三对角矩阵是非奇异矩阵的证明过程可以引证得满足条件(1)的反三对角矩阵A为非奇异矩阵[6](可逆矩阵)。
定理1对于非奇异的反三对角矩阵A都可以分解为如公式(2)形式的一个反三角矩阵与一个三角矩阵的乘积[7]。

证明:假设反三对角矩阵A可实现矩阵YH分解。利用矩阵乘法,可得

根据公式(3)可得一系列关系式如下:
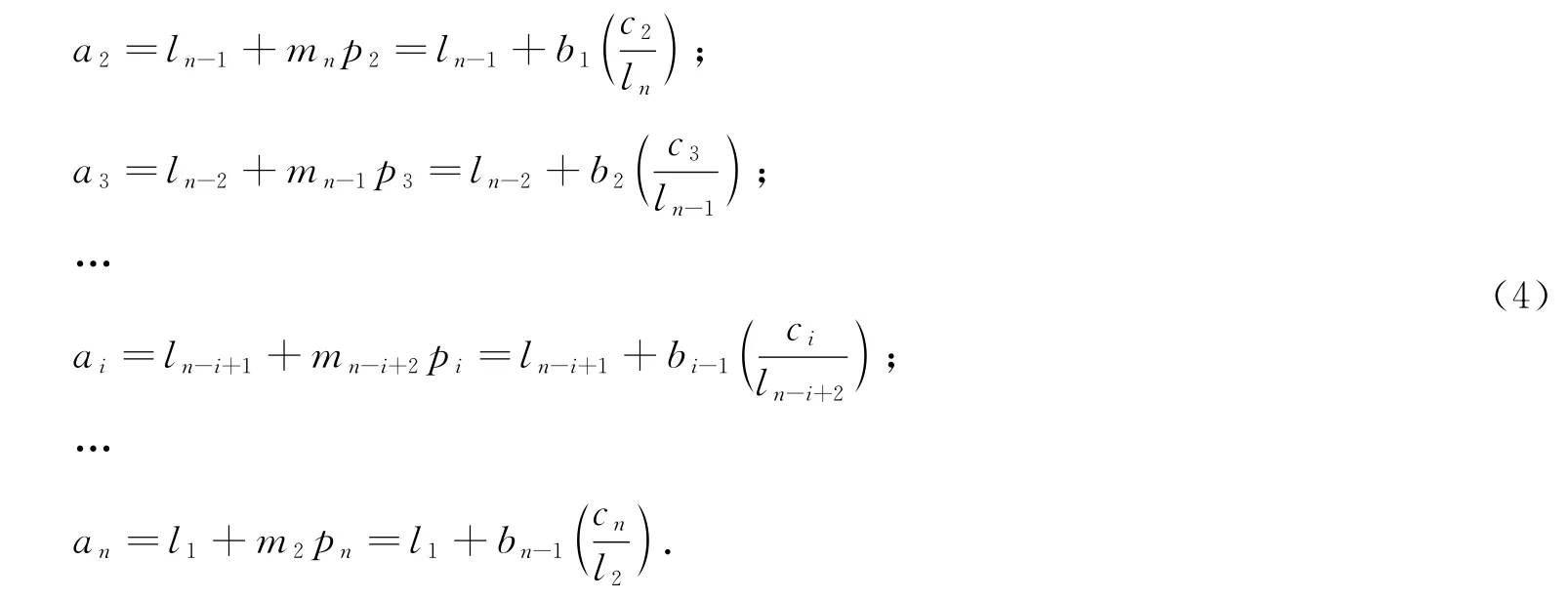
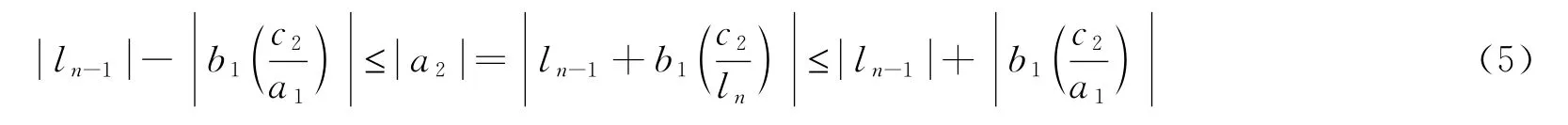
由不等式(5)及条件(1)可知
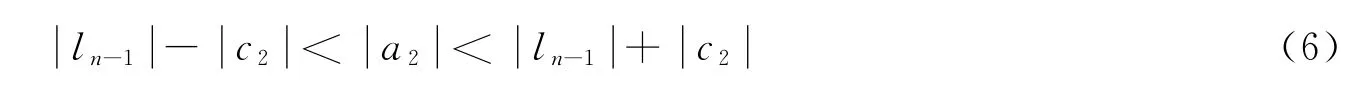
即
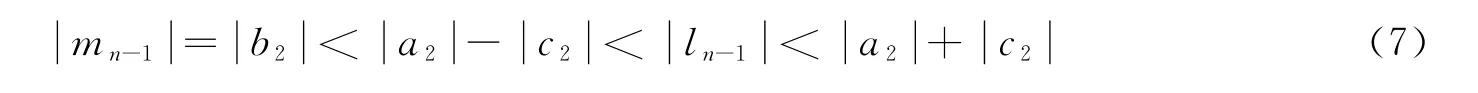
同理可证
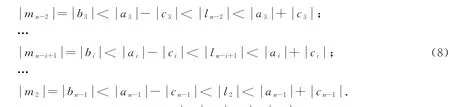
由a1=ln≠0,c2=p2ln,由公式(8)得0,同理可求得
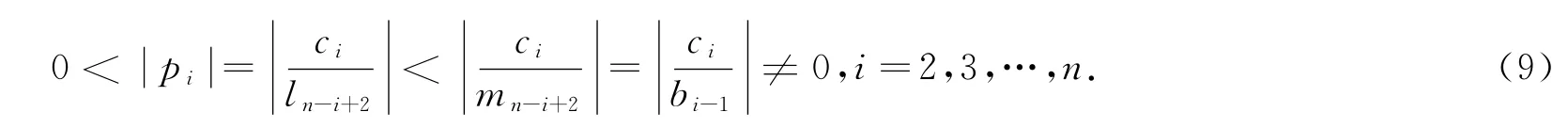
从而由公式(3)可求出pi。
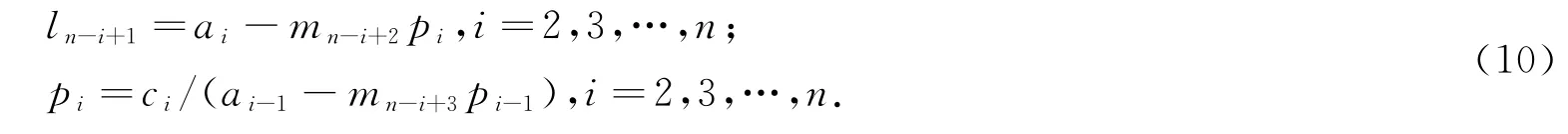
这就是说,由A的假设条件(1),完全确定了{li},{pi},{mi},实现了A的YH分解。
2 反三对角线性方程组的追赶法
在实际问题中,会经常遇到如下形式的线性方程组

这种方程组称为反三对角方程组,简记为Ax=f。
在引理1的条件下有li≠0,即追赶法可以进行计算,故将求解方程组Ax=f化为依次求解:

算法1
第1步:解方程组Yy=f,即“追”过程,算法如下:

第2步:解方程组Hx=y,即“赶”过程,算法如下:

其中li,pi,mi的计算见公式(3)。
上述算法1就是求解反三对角方程组的追赶法。又由不等式(8)的估计,即追赶法计算过程的中间变量有界,不会产生大的变化,可以有效地算出结果。
3 算例演示
用追赶法求解下列反三对角方程组:
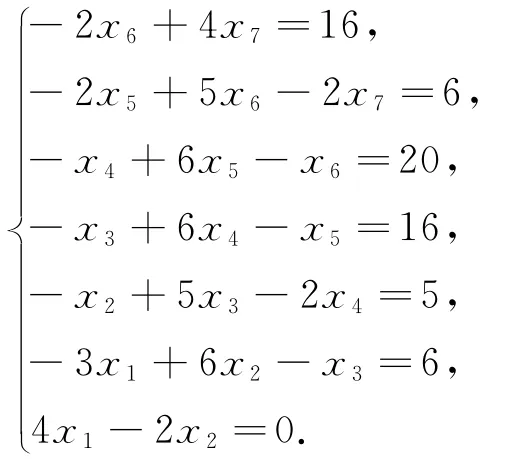
根据反三对角方程组有
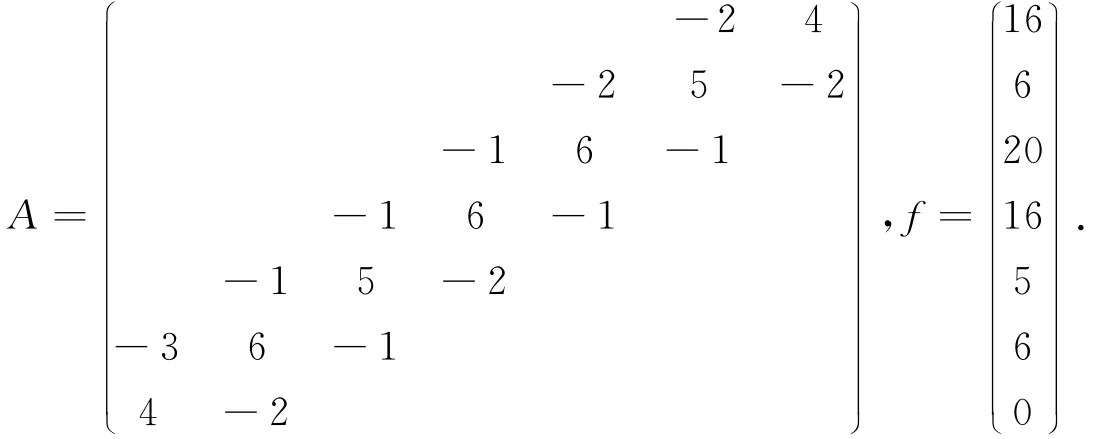
利用公式(3)可推导出
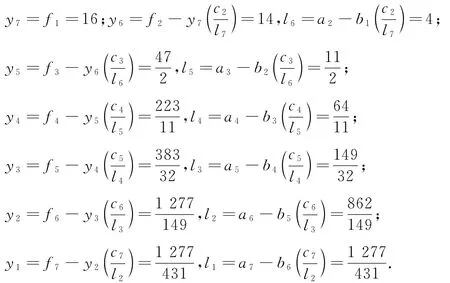
把以上结果代入公式(14),就可以得到关于xi(i=1,2,…,7)的解:
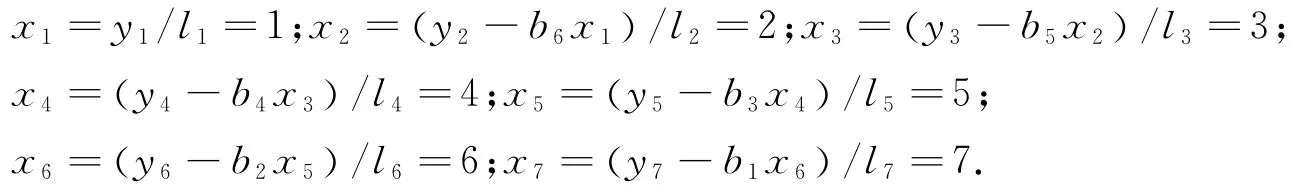
4 结论
针对反三对角方程组的特点,沿用解三对角方程组时LU分解和追赶法的基本思想,证得满足严格反对角占优的反三对角矩阵是可逆的,可以分解成YH形式并推导出了反三对角方程组的追赶法。计算结果表明,此种追赶法求解n阶反三对角方程组只需要O(5n-4)的运算量,可在线性时间内完成求解工作。
[1] 张明望.一类非单调线性互补问题的高阶Dikin型仿射尺度算法[J].数学杂志.2004,24(05):585-590.
[2] 邱茂路.矩阵约当标准化的一个新方法[J].数学杂志.2001,21(02):237-240.
[3] 李文强,马民.求解循环三对角方程组的追赶法[J].科技导报.2009,27(14):69-72.
[4] 倪有义,蔡静.反五对角与拟反五对角方程组的追赶法[J].数学杂志.2014,34(01):137-144.
[5] 杨爱民,阎少宏,夏国坤,等.求解三对角方程组的并行追赶算法[J].河北理工大学学报:自然科学版.2008,30(01):107-109.
[6] 薛正林,吴开腾.求拟反三对角线性方程组的一种数值方法[J].内江师范学院学报.2016,31(02):4-7.
[7] 关治,陆金甫.数值分析基础[M].北京:高等教育出版社,1998:254-256.
[8] 李庆扬,王能超,易大义.数值分析(第5版)[M].北京:清华大学出版社,2008:159-160.
Pursuant Method of A Kind of Special Anti-diagonal Equations and Its Realization
WU Yu-hang,YAN Shao-hong,PENG Mei-ye
(College of Science,North China University of Science and Technology,Tangshan Hebei 063009,China)
anti-tridiagonal equation;nonsingular matrix;YHdecomposition;pursuant method
The problem of solving the anti-tridiagonal equation is discussed.The definition of the antitridiagonal matrix Ais firstly given.Secondly,it is proved that meet strictly diagonally dominant antitriangular matrix is nonsingular,and then by taking advantage of the YHdecomposition of matrix method,it is concluded that the pursuant method of anti-tridiagonal equations.Finally,a numerical example is used to demonstrate.
O241.6
A
2095-2716(2016)04-0027-05
2016-05-03
2016-09-22

