岭估计在多项式曲面拟合GNSS高程中的应用

陈晓停，曹兰杰，汪金花

（华北理工大学矿业工程学院，河北唐山063009）

岭估计在多项式曲面拟合GNSS高程中的应用

陈晓停，曹兰杰，汪金花

（华北理工大学矿业工程学院，河北唐山063009）

岭估计；GNSS高程拟合；多项式曲面拟合

使用多项式曲面拟合法进行GNSS高程异常拟合时，法方程系数矩阵可能存在严重病态从而导致拟合结果不可信的问题。针对拟合过程中病态现象，应用岭估计的方法进行了拟合试验。通过唐山滦县GNSS水准网数据试验验证，结果与传统多项式曲面拟合模型相比较，岭估计方法不仅克服了法方程的病态性，而且拟合的内外符合精度较高。

当前，GNSS测量因其全方位、全天候、全时段和高精度的特点已被广泛应用于工程测量中，GNSS测量获得的高程是基于WGS－84椭球的GNSS大地高，而在实际工程应用中，地面点的高程采用正常高系统，因此通常需要将GNSS大地高转换为正常高［1］。对于小区域范围内的工程，利用多项式曲面拟合GNSS水准，计算简单且一般能够满足精度要求。

在实际应用中，由于多项式拟合模型需要的参数太多，自变量间的复共线关系增强，表现为设计矩阵严重病态。并且由于GNSS观测时间较短，卫星和接收机构成的几何图形几乎没有变化，历元之间的观测近似属于重复观测，这样就造成观测数据不足，数据之间具有相关性，而平差时是将数据作为相互独立的进行处理。这些因素都会引起误差方程的病态，进而影响解的稳定性，在处理数据时，可以使用岭估计解决这类“病态问题”［2］。

1 GNSS高程异常解算的数学模型

1．1 数学模型

高程异常为似大地水准面与参考椭球面之间的高程差，若能精确地求出GNSS网点的高程异常ζ，就可以求出GNSS点的正常高H正常。大地高H与正常高H正常的关系如图1所示。

为了求得高程异常的值，可以对测区内已知的高程异常值建立某种数学模型，将其拟合成一个曲面，得到测区内任一点的高程异常值，从而求得正常高。使用二次多项式曲面拟合进行GNSS高程拟合，则地面上任一点A（x，y）的高程异常与平面坐标的关系可以用式（1）表示：

式中，ζ为高程异常；ε是一个随机变量；f （x，y）可用下式表示：

当有n个已知点时，上式也可写成矩阵形式是：

式中，B为系数矩阵；X为估值向量；ζ为各点高程异常值。

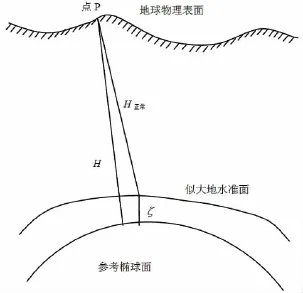
图1 大地高、正常高及高程异常的关系

1．2 平差估计方法

一般来说，解算高程异常的数学模型经常使用的平差估计方法有最小二乘估计、稳健估计和神经网络等方法。多项式拟合模型使用最小二乘估计方法经常会出现复共线性问题，岭估计可以解决这个问题。

参数X的岭估计定义为

式中：k＞0为任意常数，称为岭参数；其中N＝BTPB。

岭估计实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的耐受性远远强于最小二乘法［3］。

2 岭估计的高程异常拟合过程

2．1 处理流程

多项式曲面拟合GNSS高程时，使用岭估计进行数据处理的流程如图2所示。首先使用条件数法进行复共线性关系的诊断与度量。方阵N的条件数定义为：

式中λ是N的特征值。条件数度量了λ的散布程度，可以用来判断复共线性是否存在及其严重程度。若0＜p＜100，则认为没有复共线性；若100≤p≤1 000，则认为存在中等程度或强的复共线性；若p＞1 000，则认为存在严重的复共线性，模型病态，需要使用岭估计［4］。

图2 数据处理流程图

岭估计的关键在于岭参数的选取。平差估计方法选择岭估计是为了减少均方误差，提高估计准确度，所以应该选择使均方误差达到最小的岭参数［5］。但是岭参数k的最优值依赖于未知参数，并且这种依赖关系没有显式表示，这使得k的确定变得十分困难［6］。确定k值的方法有许多种，本试验使用双h公式法确定岭参数k值。双h公式法因公示中含有两个可选择的参数h1，h2而得名，可简化为h1＝t，h2＝0，文中所提到的大地高H与正常高H正常是大地测量学中的专业术语。使用双h公式法求岭参数k，首先使用最小二乘法计算XLS以及σ2LS，代入到公式（6）求出k的取值。

式中，t为必要观测元素的个数，XLS为在最小二乘原则下对模型进行求解得出的参数，σ2LS为使用最小二乘方法求得的方差因子。

3 应用实例

3．1 数据来源

数据来源于唐山市滦县的实测资料，试验数据分布范围较大，其中一部分点分布在山区，一部分点分布在平原地区。位于平原地区的点高程变化较小，GNSS大地高的高程最大值为40．404 0，最小值为30．136 6。位于地面起伏较大的山区的点，高程变化剧烈，GNSS大地高的高程最大值为210．644 6，最小值为39．778 1。

测区共布设了63个GNSS点，其中26个点联测了四等水准。在本试验中，其中的21个点作为参与拟合的已知点，而余下的5个点作为外部检核点，分别是68、03、09、25、43。试验分别采用最小二乘法平差多项式曲面拟合法和岭估计法进行参数解算。试验的原始数据如下，由于数据保密需要，部分数据进行了处理，这些点的分布如图3所示。

图3 点位分布图

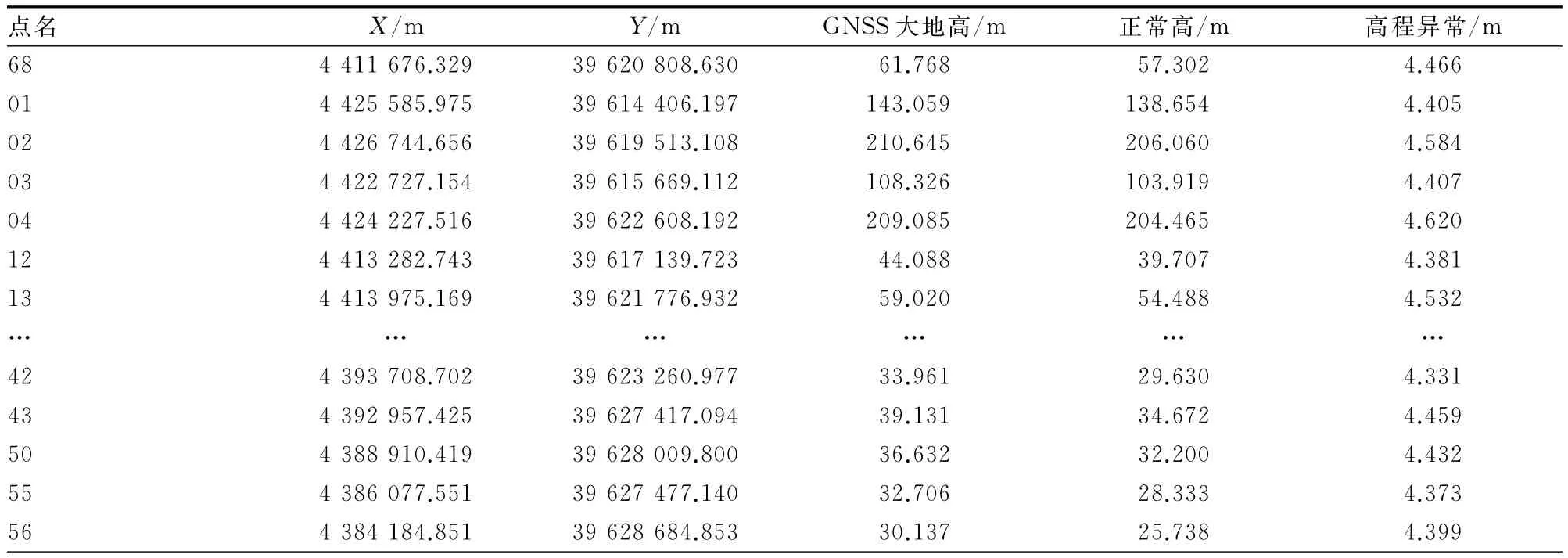
表1 部分试验数据

3．2 2种平差方法的比较

为了便于比较最小二乘法和岭估计，使用外符合精度和内符合精度来客观地评价GNSS水准计算的精度。由参与拟合计算已知点的高程异常值与拟合值的差即拟合残差，按式（7）计算得到。内符合精度可以查看模型得到的拟合值与已知点的高程异常值是否相符，判断模型的优劣。

根据参与检核点的高程异常值和拟合值之差，按式（8）来计算2种方法的精度，即得到外符合精度M。外符合精度用于评价预测模型的好坏，代表了对未知点高程异常进行预测的一致性。

式中，V为外部检核点高程异常的拟合值与真实值的差值；n为检核点的个数。

在本试验中，其中的21个点作为参与拟合的已知点，而余下的5个点，分别是C068、LⅢ03、LⅢ09、LⅢ25和LⅢ43，不参与方程解算，作为外部检核点用于检核。检核点在山区和平原均有分布，与两处的已知点个数成正比，点位分布合理，且都位于控制网内侧。在计算过程中发现法方程矩阵的最大特征值除以最小特征值的值，即条件数为8．385 3e＋45，则法方程矩阵呈严重病态性。按照双h公式法求得k＝2．693 7e－09，2种方法分别对高程异常进行拟合，计算结果如表2所示。

表2 计算结果比较

由表2可以看出，对于GNSS高程拟合，基于最小二乘法的多项式曲面模型最为常用，其方法简单，但精度较低，并且严重偏离真值。最小二乘的均方误差为9．833 2e＋15，内符合精度为61．439 3，得到的残差都很大，根本不可用。使用岭估计平差方法的多项式曲面拟合，解决了函数法方程的病态问题，内外符合精度大大高于最小二乘估计方法的多项式曲面拟合。岭估计的均方误差为5．291 2e＋04，远远小于最小二乘法的均方误差，得到的高程异常拟合值接近真值，其拟合点的残差很小，检核点的残差均小于40mm，满足四等水准限差，可供工程使用。

4 结论

通过实例计算验证了岭估计方法在多项式曲面拟合GNSS高程中的优越性，表明双h公式法求岭参数不仅应用在曲面拟合中是可行的，而且效果显著，解决了法方程矩阵呈现病态这一问题。虽然测区内控制点数量有限，且由于地形点位分布不够均匀，难免对试验结果产生一定的影响，但是仍可以看出，岭估计方法很好地改进了最小二乘原则下的多项式曲面拟合，内外符合精度大大提高，并能满足四等水准测量的精度要求，比传统的最小二乘法更适合于多项式曲面拟合GNSS高程。

参考文献：

［1］ 汪金花，刘雨青，吴长悦．一种含稳健权的神经网络GNSS高程拟合模型［J］．测绘通报，2014，（08）：14－16．

［2］ 来园莉．关于岭估计的若干问题研究［D］．武汉：武汉科技大学，2010．

［3］ 陈正宇，徐君民．基于岭估计的GPS水准多项式拟合方法研究［J］．工程勘察，2014，（10）：66－68．

［4］ 郝卫峰．测量数据处理中病态性问题［D］．湖南：中南大学，2008．

［5］ 王乐洋，许才军，鲁铁定．病态加权总体最小二乘平差的岭估计解法［J］．武汉大学学报（信息科学版），2010，35（11）：1346－1350．

［6］ 吴杰，李明峰，余腾．测量数据处理中病态矩阵和正则化方法［J］．大地测量与地球动力学，2010，30（4）：102－105．

Application of Ridge Estimation in Polynomial Surface Fitting of GNSS Height

CHEN Xiao－ting，CAO Lan－jie，WANG Jin－hua
（College of Mining Engineering，North China University of Science and Technology，Tangshan Hebei 063009，China）

ridge estimation；GNSS height fitting；polynomial surface fitting

When fitting the GNSS height anomaly with polynomial surface fitting method，the coefficient matrix of the normal equation may be seriously ill－conditioned，which leads to the problem that the fitting result cannot be trusted．The double h formula method of ridge estimation is used to solve the problem in the process of fitting．The experiment data is from the GNSS network in Luanxian County of Tangshan．The result shows that，compared with the traditional polynomial surface fitting model，ridge estimation not only overcomes the ill condition of the normal equation，but also has higher inner and outer fitting precision．

TD173＋．2

A

2095－2716（2016）04－0001－06

2016－05－19

2016－09－26

唐山市科技支撑项目（13130218Z）。