江西省各地级市经济状况的系统聚类分析研究

王乐洋,　郭　健,　熊露雲,　余　航

(1.东华理工大学 测绘工程学院，江西 南昌 330013；2.国家测绘地理信息局 重点实验室流域生态与地理环境监测，江西 南昌 330013)



江西省各地级市经济状况的系统聚类分析研究

王乐洋1,2,郭健1,熊露雲1,余航1

(1.东华理工大学 测绘工程学院，江西 南昌 330013；2.国家测绘地理信息局 重点实验室流域生态与地理环境监测，江西 南昌 330013)

摘要：选取反映区域经济发展状况的8个主要指标，以系统聚类分析方法研究江西省各地级市的经济状况，对系统聚类分析下的结果进行比较。研究认为江西省各地区的经济发展水平主要可分为四类：第一类包括南昌，第二类包括景德镇、萍乡、鹰潭，第三类包括九江、赣州、吉安、宜春、抚州、上饶，第四类包括新余。研究结果表明，江西省北部、中南部的地级市间经济水平差距显著，建议应该对中南部地区发展给予更多的重视。

关键词：经济状况；现代地理学；聚类分析；系统聚类

王乐洋,郭健,熊露雲,等.江西省各地级市经济状况的系统聚类分析研究[J].东华理工大学学报：社会科学版，2016，35(1)：14-19.

Wang Le-yang, Guo Jian, Xiong Lu-yun, et al.The hierarchical cluster analysis of the regional economic situation in Jiangxi province[J].Journal of East China University of Technology(Social Science)，2016，35(1)：14-19.

经过改革开放三十多年的飞速发展，江西省的经济发展取得了重大成果，但由于各地区的资源、环境条件，所处的地理位置以及各地区政策的差异，致使江西省各地级市的经济状况表现出明显的区域差异[1，2]。对经济差异区域进行科学、有效地分类，有利于经济政策的针对性与合理性[3-5]。本文基于现代地理学中的数学方法，以系统聚类分析方法研究江西省各地级市的经济状况，采用目前公认的多指标评价体系，进行极差标准化处理，选取欧氏距离，通过最短距离法计算出类与类之间的距离，并对聚类后的结果进行分析。

1系统聚类分析方法

1.1系统聚类的基本原理

对于一组对象，定义其对象之间的距离，然后将这组对象分成不同类，通过计算对象之间距离，并将每一次聚类距离之间最小的两个类归并，将归并后的类与其他类再次进行距离计算，得出的新类与其他类之间距离最小的再次合并为一类，依次类推，得出一个大类[5]。

1.2聚类要素的数据处理

对于聚类分析而言，其结果的可靠度、准确度与要素的选择息息相关。在研究地域分类分区中，被聚类的对象往往是由多种要素组成的。数据往往是不同的元素有不同的量纲与量级，它们数值的变化可能性大，这样的分类将一定程度影响结果的准确度[4]。因此，在进行聚类分析之前，第一步要做的就是对聚类要素进行数据处理即标准化。

本文对原始数据进行了极差标准化转换，即对被标准化项目的每个取值减去其最小值，然后除以最大值与最小值的差，新数据各要素的极大值为1，极小值为0。若聚类的对象有m个，相应聚类对象包含n个要素。其计算公式为[4]：

(1)

1.3对象之间距离的计算

差异越小，对象之间的距离越小；反之，差异越大，对象之间的距离越大。距离是系统聚类的依据，由于距离可以衡量事物之间的差异。若是将其中每一个分类对象中的n个聚类要素看成n维空间的n个坐标轴，那么每一个分类对象中的n个要素构成的n维数据向量就是n维空间中的一个点[4]。如此，对应的n维空间中点之间的距离可以用来量度分类对象之间的差别。本文计算分类对象之间的距离采用了欧氏距离。计算公式如下[4]：

(2)

1.4最短距离聚类法

最短距离聚类法，是在原来的m×m距离矩阵的非对角线元素中找出dpq=min{dij}，把分类对象Gp和Gq归并为一类Gr新然后按公式(3)

drk=min{dpd,dqk}(k≠p,q)

(3)

计算原来各类与新类之间的距离，得出一个新的m-1阶距离矩阵；从新的距离矩阵中选出最小者dij，把Gi、Gj归并成新类；再计算各类与新类的距离，循环计算，直至各分类对象被归为一类为止[4]。

2江西省各地级市经济状况的系统聚类案例

2.1聚类要素的数据处理

本文用统计分析SPSS软件，参照2011—2012年江西统计年鉴[6，7]，对2010—2011年江西省11个地级市的8项经济指标进行系统聚类分析运算，这8项经济指标包括：地区总产值、第一产业、工业、建筑业、交通运输仓储和邮政业、批发零售和住宿餐饮业、金融业、人均地区生产总值，具体见表1、表2。分析过程中，对原始变量进行了极差标准化处理，用欧氏距离定义对象之间的距离，并采用最短距离法定义类别。

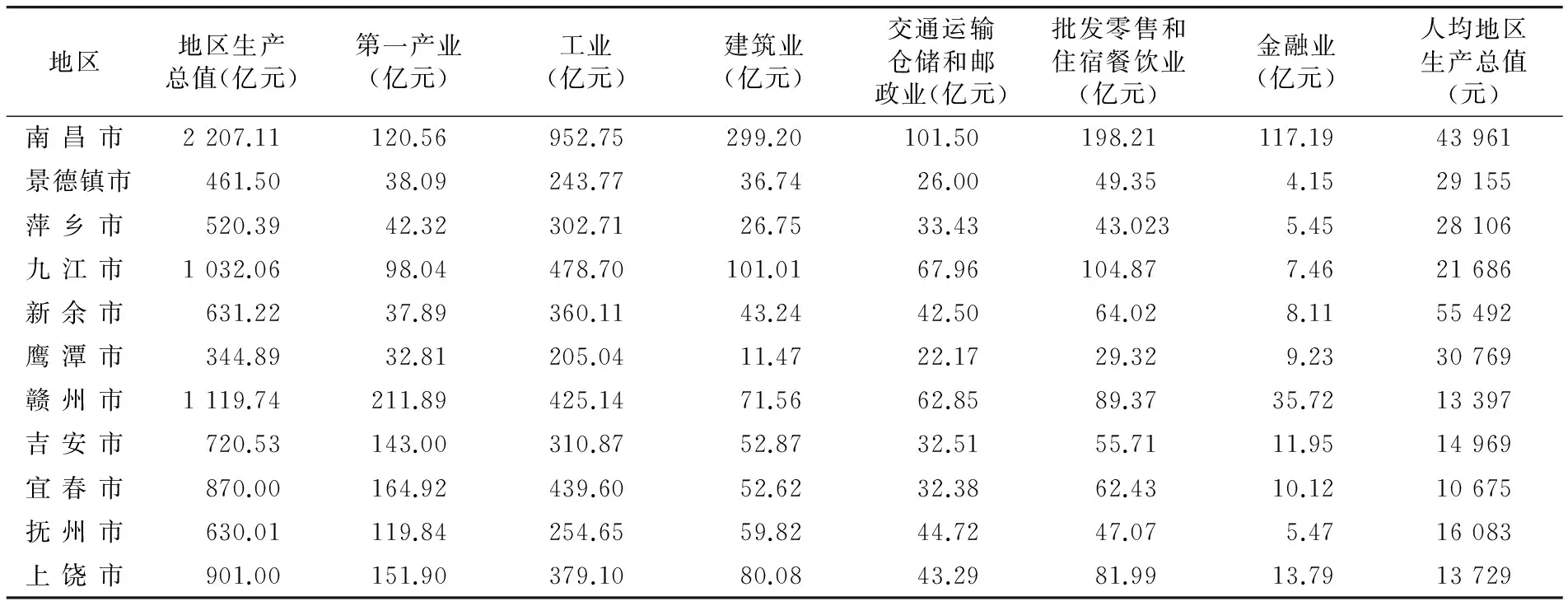
表1　2010年江西省11个地级市各项经济指标

表2　2011年江西省11个地级市各项经济指标

2.22010年经济指标的系统聚类分析

聚类分析计算过程如表3和图1所示。由表3可知，该表第一列表示聚类分析的步骤，其中1～11依次表示南昌、景德镇、萍乡、九江、新余、鹰潭、赣州、吉安、宜春、抚州、上饶。而群集组合群集1、2表示某步聚类分析中哪两个对象或类聚成了一类。第四列表示对象之间的距离，距离越小，优先聚类。首次出现阶群集1、2表示在某步聚类涉及的类型，0表示对象，不小于1的数字m表示本步与第m步聚类产生的新类聚类。最后一列则表示该步聚类结果在下面聚类过程中第几步中将用到。

图1清晰地表示了聚类分析的全过程，经过10步聚类之后11个对象最终聚成了一大类。在该图中，距离标尺上根据需要(粗分或细分)选择一个划分类的距离值，垂直标尺划线，垂线与水平连线相交的交点数即为分类的类别数，相交水平连线所对应的各案聚成一类[5]。

表3　2010年江西省11个地级市聚类表

然而对于经济类型区划分，既不是越多越好，也不是越少越好。分区太多，就失去了分区的意义；分区太少，则很难做到分类指导和有的放矢。为了更加明显地体现江西省各地区的经济差异，更准确地为各地区的经济发展程度定位，结合江西省的实际情况，可将11个地级市的经济发展状况分为四类，如图1中粗竖线位置所示，具体分类情况如表4。

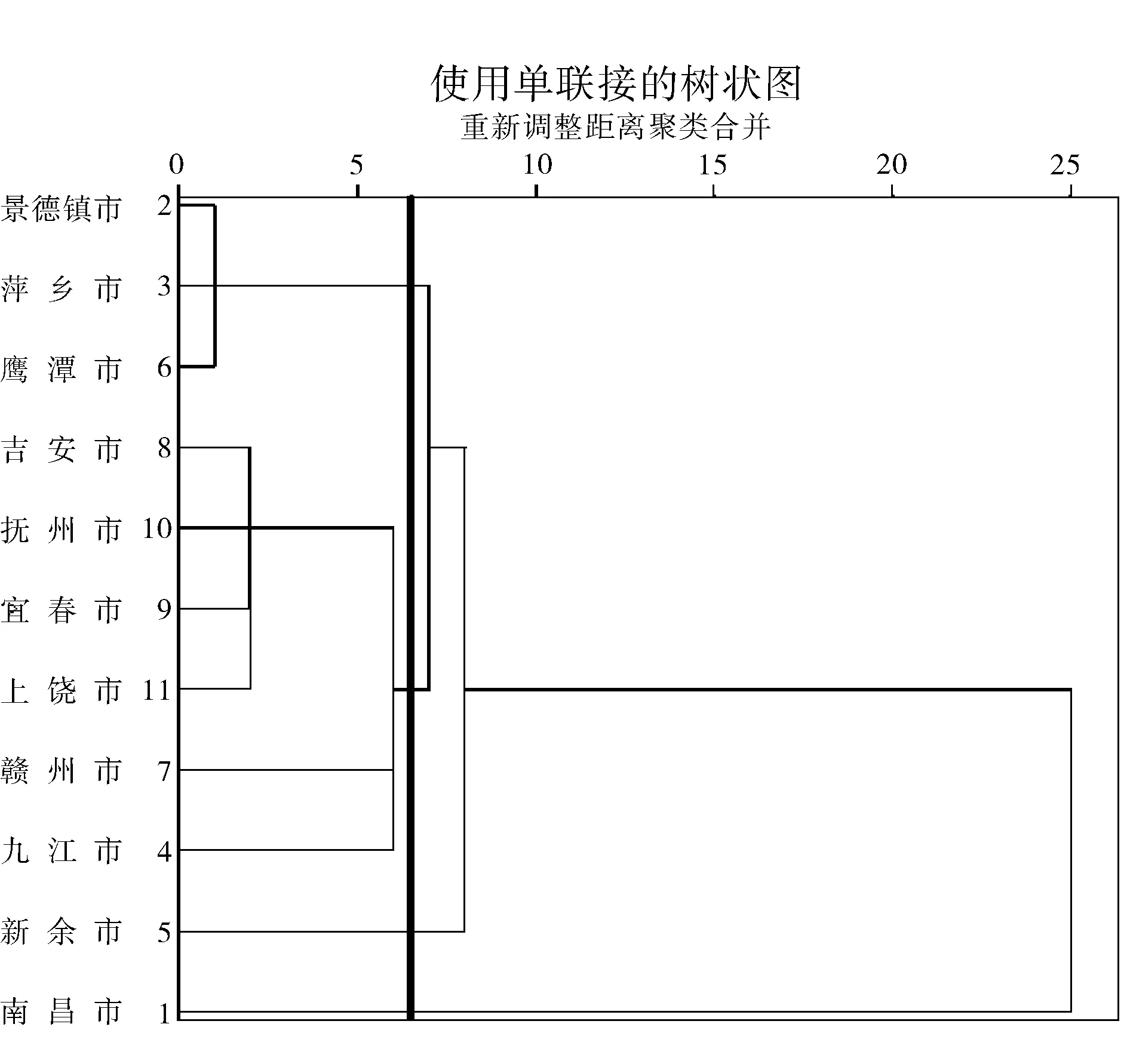
图1　2010年江西省11个地级市系统聚类树状图

类型地级市第一类南昌市第二类景德镇市、萍乡市、鹰潭市第三类九江市、赣州市、吉安市、宜春市、抚州市、上饶市第四类新余市

本文还进行了OLAP(在线分析过程)分析，分析结果见表5，其主要用于对统计数据进行描述性分析，可以从均值、标准差等方面简单直观地研究各类别之间的区别。结合表3和图1可知，第一类只有南昌这一个地级市，它的多项指标(均值)比其它类高，其第一产业相比于第三类较低，人均地区生产总值低于第四类；第二类的地级市的多项指标低于第三类，但人均地区生产总值高于第三类；第三类的地级市的多项指标低于第一类，却高于第二、四类，然而人均地区生产总值均值为全省最低；第四类的新余市，多项指标介于第二、三类之间，但是人均地区生产总值均值却为全省最高。

2.32011年经济指标的系统聚类分析

表6和图2给出了2011年江西省11个地级市的聚类过程，分类情况与2010年相同，在此不再赘述。

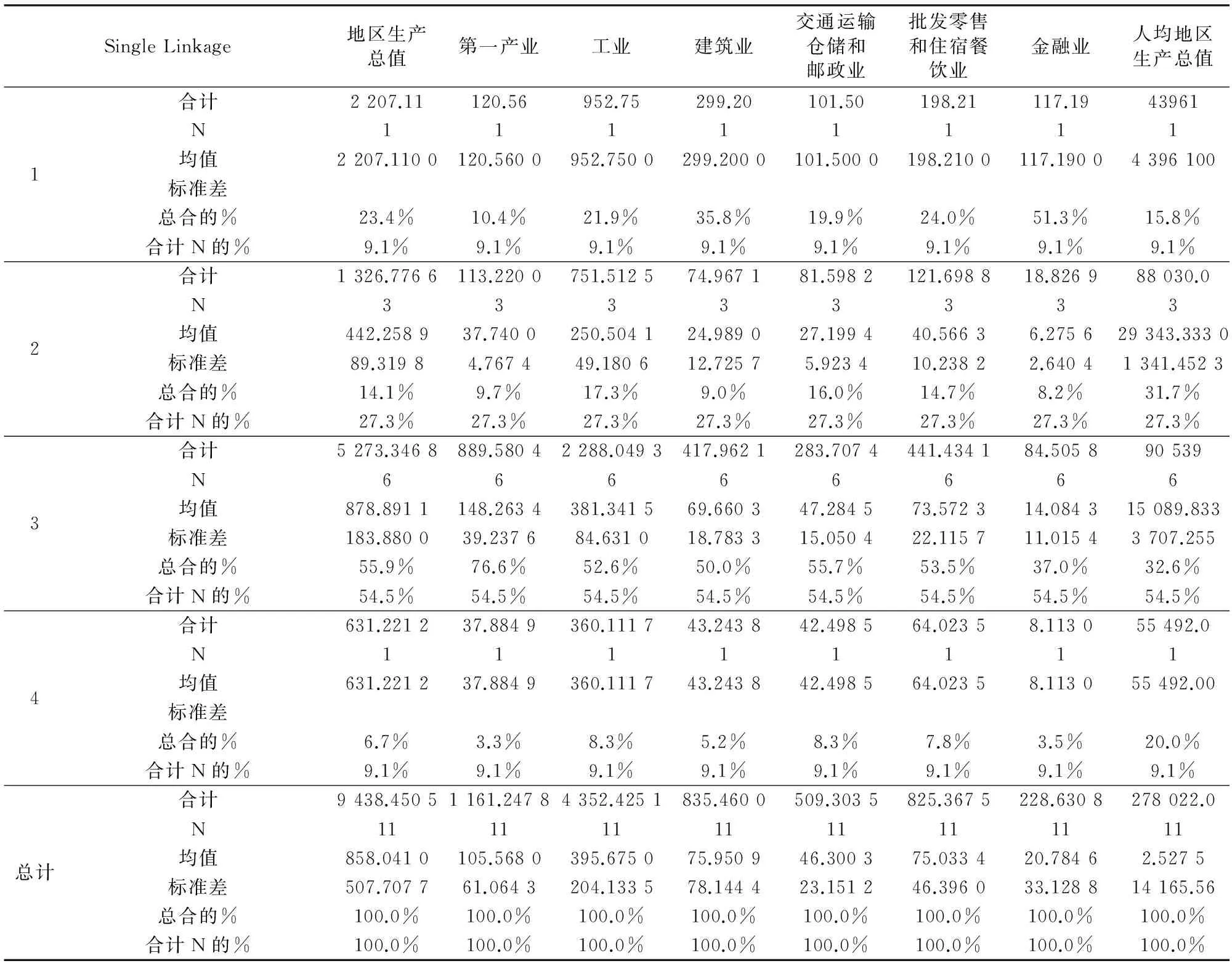
表5　2010年江西省11个地级市系统聚类结果的OLAP立方体

根据2011年江西省11个地级市系统聚类结果的OLAP立方体(见表7)和各项经济指标数据可知，各类经济区的各项指标相比于2010年都有增长，但是各类地级市经济指标的高低情况与2010年情况基本一致，其分类结果也与2010年相同。

表6 2011年江西省11个地级市聚类表阶群集组合群集1群集2系数首次出现阶群集群集1群集2下一阶1230.1300022260.17510839110.2140044890.23003558100.2324066780.5180577470.5460688240.5832799250.663801010121.754090图2 2011年江西省11个地级市系统聚类树状图

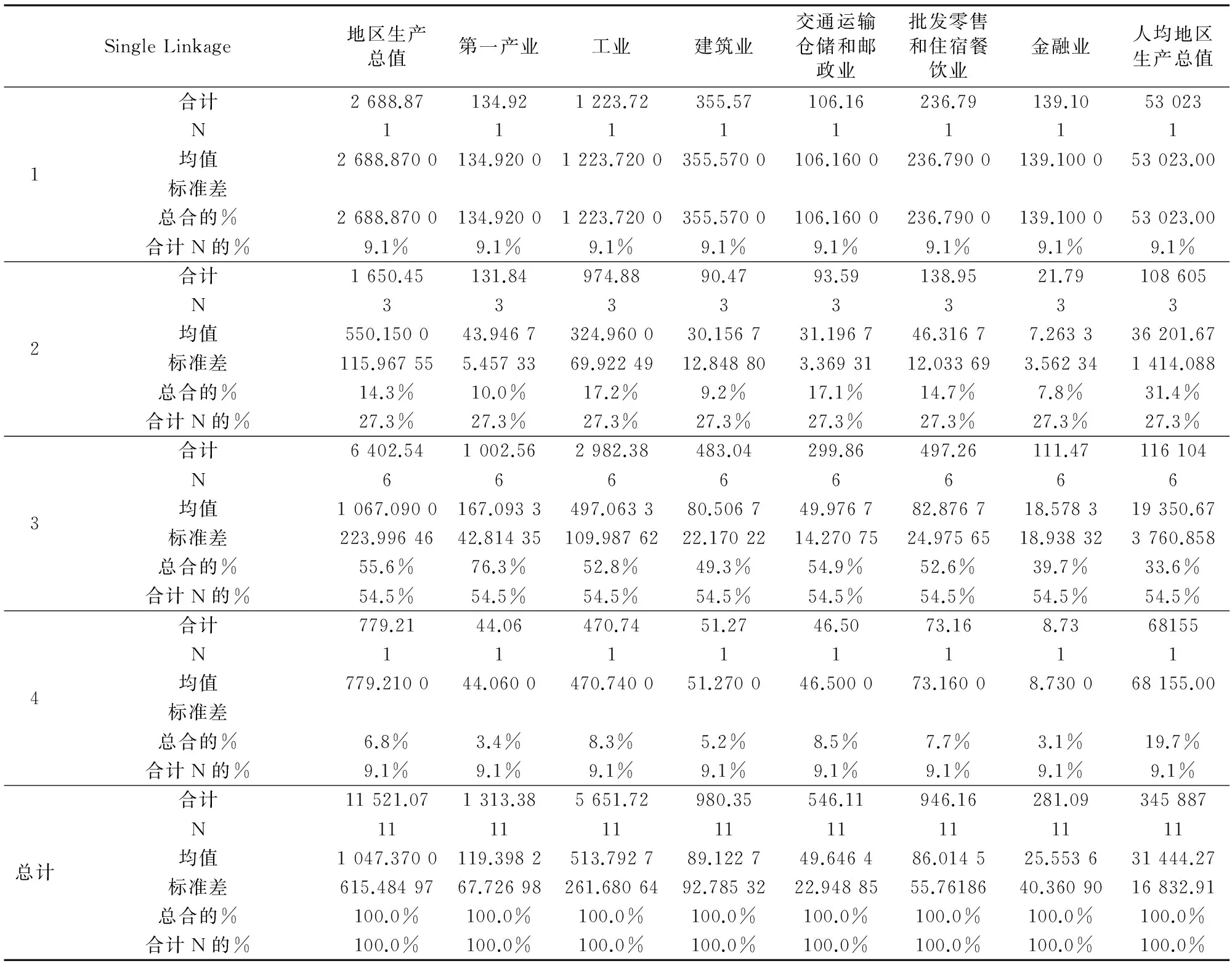
表7　2011年江西省11个地级市系统聚类结果的OLAP立方体

3结论

本文利用系统聚类分析，基于多元统计与现代地理学中的数学方法，来研究江西省11个地级市经济发展实际情况。其中第一类的南昌与江西其他10个地级市有着巨大的差异性。由2010—2011年江西省11个地级市系统聚类结果的OLAP立方体和2010—2011年江西省11个地级市各项经济指标数据统计可知，它的多项指标如：地区生产总值、工业、建筑业、交通运输仓储和邮政业、批发零售和住宿餐饮业、金融业均处于首位。因此，作为江西省经济龙头的南昌，要增强区域间的合作与优势互补，带动其它地级市经济发展，达到共同发展的目的。

第二类包括景德镇、萍乡、鹰潭，这3个城市是除新余之外面积最小的3个地级市，人均地区生产总值位于前列。这三座城市应该积极引进和吸收先进的技术和管理经验，改造传统产业，发展高技术产业，促进城市经济结构的优化和产业结构的升级。

第三类包括九江、赣州、吉安、宜春、抚州、上饶，这六个城市经济情况大体相差不大，但在不同的经济指标上的差距也显而易见。在这6个城市中又可划分为2亚类，第一亚类包括赣州、九江，第二亚类包括吉安、宜春、抚州、上饶。第一亚类的九江市在工业、建筑业、交通运输仓储和邮政业、批发零售和住宿餐饮业、人均地区生产总值强于赣州，但是赣州在其他指标中高于九江，地区生产总值在11个地级市中排名第二，第一产业排名第一，人均地区生产总值却是倒数第一至三位，显示出赣州经济底子薄。第二亚类中吉安市和抚州市的地区生产总值、第一产业、工业、批发零售和住宿餐饮业、金融业都低于宜春市和上饶市。这6个城市的人均地区生产总值是江西省11个地级市的中较低的，经济指标的低迷说明城市的经济结构急需调整。

第四类包括新余市。新余市虽然由于其面积的偏小导致经济总量不大，但是新余市的人均地区生产总值仅次于南昌，排名全省第二。这与其较好的工业发展体系和较高的城市化水平是分不开的。新余市应当继续保持这种经济发展的势头。

本文依托数理统计工具，将江西省11个地级市按经济发展水平分为四类，可以看出江西省各类地级市间经济水平差距显著，这将有助于提高我们对各地区经济发展状况的认识，同时为相关政策的制定提供参考依据。由于本文选取的分类指标相对较少，要反映一个地区经济发展水平，更合理的模型应该考虑更多的指标，建立一个更加完善、合理的分类指标体系。

[参考文献]

[1] 彭萍,胡桂开.江西省经济区划及分区发展研究[J].东华理工大学学报:社会科学版，2008(2):130-132.

[2] 雷芳,邱卫林.城乡统筹发展视角下环鄱阳湖生态经济区的价格障碍分析[J].东华理工大学学报:社会科学版,2011(4):327-330.

[3] 王斌会.多元统计分析及R语言建模[M].广州:暨南大学出版社，2010：50-60.

[4] 徐建华.现代地理学中的数学方法[M].北京:高等教育出版社，2002：69-72.

[5] 王薇.对我国各省市2008年经济状况的聚类分析[J].经济师，2010(3)：87-89.

[6] 江西省统计局，国家统计局江西调查总队.江西统计年鉴2011[M].北京:中国统计出版社，2011.

[7] 江西省统计局，国家统计局江西调查总队.江西统计年鉴2012[M].北京:中国统计出版社，2012.

收稿日期：2015-12-08

基金项目：国家自然科学基金(41204003)；测绘地理信息公益性行业科研专项(201512026)；江西省自然科学基金(20151BAB203042)；江西省教育厅科技项目(KJLD12077，KJLD14049)；流域生态与地理环境监测国家测绘地理信息局重点实验室项目(WE2015005)；对地观测技术国家测绘地理信息局重点实验室项目(K201502)；东华理工大学博士科研启动基金(DHBK201113)。

作者简介：王乐洋(1983—)，男，山东临沂人，博士，副教授，硕士生导师，主要从事大地测量反演及总体最小二乘平差的理论与应用研究。

中图分类号：F224；F127

文献标识码：A

文章编号：1674-3512(2016)01-0014-06

The Hierarchical Cluster Analysis of the Regional Economic Situation in Jiangxi Province

WANG Le-yang1,2,GUO Jian1,XIONG Lu-yun1,YU Hang1

(1.FacultyofGeomatics,EastChinaUniversityofTechnology,Nanchang330013,China;2.KeyLaboratoryofWatershedEcologyandGeographicalEnvironmentMonitoring,NASG，Nanchang330013,China)

Abstract:The paper selects eight major indicators that can reflect regional economic development and uses cluster analysis method to study the economy situation around the cities of Jiangxi province. Under the comparison of the results, the study suggests that the level of economic development in Jiangxi province can be divided into four categories. The first category is Nanchang. The second includes Jingdezhen, Pingxiang, Yingtan, the third Jiujiang, Ganzhou, Ji’an, Yichun, Fuzhou, Shangrao, and the last Xinyu. We find that there are significant difference in the economic level between the northern cities and south central cities. The government should attach more importance to the development of south central areas.

Key Words:economic conditions; modern geography; cluster analysis; hierarchical clustering