考虑波速影响的斜拉桥非一致激励地震响应研究

张凡+颜晓伟+李帅+王景全

摘要：为研究地震波传播速度对大跨度斜拉桥地震响应的影响，以某主跨跨长406 m的双塔钢箱梁斜拉桥为研究对象，建立动力有限元模型。对非一致地震激励输入方法进行理论分析，对比研究了相对运动法、大刚度法和大质量法的计算特点。通过对视波速无穷大时非一致激励法与一致激励法的计算结果进行对比，校验地震动输入方法的正确性。在此基础上，分别选择天津地震波、El Centro地震波和汶川地震波，根据软土区和岩石区地震波传播特点，对视波速在50～4 000 m·s-1之间的不同波速工况进行计算。结果表明：波速对斜拉桥地震响应有显著影响，软土区视波速对结构影响更加突出，对位于深厚软土区的大跨度斜拉桥进行行波效应分析时，需要关注结构的内力和位移响应，而岩石区仅需关注结构的内力响应。

关键词：桥梁工程；相对运动法；大跨度斜拉桥；行波效应；多点激励；视波速

中图分类号：U448.27文献标志码：A

Abstract： In order to investigate the effects of propagation velocity of ground motions on the seismic response of cablestayed bridge， a cablestayed bridge with span length of 406 m was taken as an example and the dynamic finite element model was built. The multisupport excitation method was analyzed theoretically， and the characteristics of the relative motion method， the large mass method and the large stiffness method were compared. When the current wave velocity is infinity， the calculation results under asynchronous excitation were compared with those under uniform excitations to verify the accuracy of the method of ground input. On this basis， considering the different characteristics of ground motions in soft soil area and rock area， Tianjin wave， El Centro wave and Wenchuan wave were chosen with different propagation velocities ranging from 50 m·s-1 to 4 000 m·s-1. The results show that different velocities have significant influence on seismic response of cablestayed bridge， and the influence of apparent wave velocity on structure is more prominent in soft soil area. The internal force and displacement should be considered when longspan cablestayed bridge in deep soft soil area is analyzed， while the internal force will be only concerned in rock area.

Key words： bridge engineering； relative motion method； longspan cablestayed bridge； wavepassage effect； multisupport excitation； apparent wave velocity

0引言

由于斜拉桥跨度大，自振周期长，考虑到地震动的空间变异性特征，一致激励已不能满足工程抗震需求，采取非一致激励分析方法可更好地反映出结构响应规律。Housner[1]很早注意到了这一问题，1965年Bongdanoff等[2]率先研究了行波效应对大跨度结构的影响。直到1980年，Pandey等[3]开始尝试研究斜拉桥多点激励的问题。1983年项海帆[4]以天津永和桥为对象进行了斜拉桥的行波效应研究，认为支承处的非同步激励使动力反应部分减小甚多，行波效应对于飘浮体系的斜拉桥是有利的。1992年Nazmy等[5]分别对主跨跨长335 m和跨长670 m的斜拉桥进行了分析，认为行波效应在低波速区会增大斜拉桥的地震响应，且行波效应对大跨柔性斜拉桥影响并不明显。2010年武芳文等[6]采用随机振动分析方法，选取4种不同的视波速对苏通大桥进行了行波效应分析，研究表明行波效应的影响与结构自身动力特性、视波速、构件位置及研究响应类型（位移与内力）均有明显相关性。以上学者以视波速为单一参数，分析了行波效应对结构地震响应的影响，但均未关注场地类型不同所引起的结构响应的差异。近些年，各国学者已关注到场地条件对结构响应的影响。Soyluk等[7]将场地条件划分为硬土区、中等土区和软土区，选取200～1 800 m·s-1的视波速区间，采用随机振动方法对某主跨跨长344 m的斜拉桥做了行波效应分析。许莉等[8]对一主跨跨长680 m的斜拉桥进行了行波效应分析，视波速变化区间为100～3 000 m·s-1，并按4种不同的场地情况进行结构响应分析。陈幼平等[9] 认为视波速与场地条件是相关的，视波速区间随着场地条件变化，基于此对天津永和桥进行了3D行波效应研究，发现斜拉桥在考虑行波效应的三向正交地震作用下关键截面的位移和内力均增大。综上所述，各国学者对大跨度斜拉桥多点激励下的地震响应研究所得结论迥异，且在考虑场地条件的行波效应分析时，大多学者将视波速和场地条件作为不相关的参数来考虑。因此，有必要研究场地差异和行波效应对大跨结构地震响应的影响规律。

为研究行波效应对大跨度斜拉桥地震响应的影响，首先对比分析了非一致地震激励输入方法（相对运动法、大刚度法和大质量法）的计算特点。在此基础上，以某175.4 m+406 m+175.4 m的双塔双索面斜拉桥为工程背景，采用通用有限元软件MIDAS/Civil建立动力有限元模型，通过对视波速无穷大时非一致激励法计算结果与一致激励法计算结果进行对比，校验地震动输入方法的正确性。以天津地震波、El Centro波和汶川波作为地震动输入，根据软土区和岩石区地震波传播特点，将软土区视波速分为50～250 m·s-1之间的6种工况，岩石软土过渡区视波速分为250～2 000 m·s-1之间的5种工况，岩石区视波速分为2 000～4 000 m·s-1之间的3种工况进行计算，以研究场地条件和视波速对斜拉桥地震响应的影响程度。

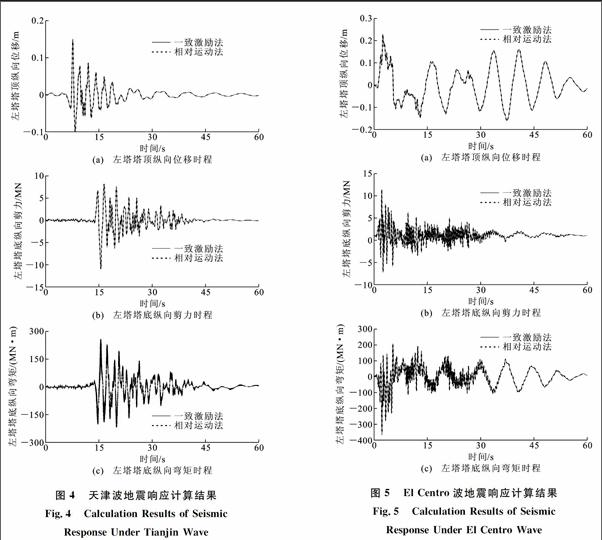
由计算结果可知，采用一致激励法和相对运动法计算出的结构地震响应具有较好的一致性，3组地震波作用下塔顶纵向位移、塔底剪力和弯矩动力响应几乎完全一致。因此，采用相对运动法可有效实现多点激励，采用该方法进行行波效应分析具有较好的可靠性。

3波速影响下行波效应地震时程分析

3.1一致激励计算结果分析

首先分析地震动一致激励作用下该桥的地震响应规律，将所选地震波分别输入计算模型，主要关注该桥塔顶位移、塔底内力和主梁跨中位移。提取一致激励法计算的结构关键部位地震响应峰值，见表2，3。

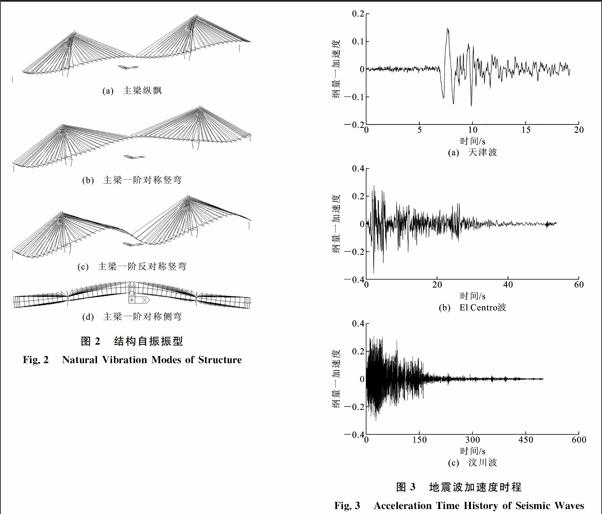
由表2，3可知，一致激励下该桥主要表现为全桥的纵向振动，横向位移和竖向位移接近于0，横桥向剪力和弯矩较小。一致激励地震作用下左塔和右塔的地震响应峰值相同，到达峰值的时间也相同，主梁跨中竖向位移和轴力接近于0，符合对称结构的响应特点。

3.2多点激励下的地震时程分析

研究表明，地震波在软土区的传播速度为50～250 m·s-1，在岩石区的传播速度为2 000～2 500 m·s-1[5]。为了研究斜拉桥地震响应与地震波传播速度之间的关系，本文选取视波速为50，75，100，150，200，250，300，450，600，800，1 000，2 000，3 000，4 000 m·s-1的地震波，分析该桥的地震响应，引入影响系数（多点激励计算结果与一致激励计算结果的比值），比较行波效应与一致激励对斜拉桥地震响应的影响。

3.2.1视波速对塔顶位移的影响

图7给出了塔顶位移响应与视波速的关系曲线（图7中，WE表示行波效应，UE表示一致激励，TJ表示天津波，WCH表示汶川波，El表示El Centro波）。通过计算分析可知，不同地震波作用下塔顶位移峰值随视波速的变化规律均相同。天津波和汶川波作用下考虑行波效应的位移峰值均小于一致激励下的位移峰值，El Centro波作用下考虑行波效应的位移峰值均大于一致激励下的位移峰值。在软土区，汶川波和天津波的最小影响系数分别为0.25和0.69，El Centro波的最大影响系数为2.68；在岩石区，塔顶纵向位移峰值接近于一致激励的位移峰值。考虑行波效应时，3组地震波作用下斜拉桥塔顶横向位移峰值均大于对应的一致激励下的位移峰值，但因在纵向地震作用下塔顶横向位移相对于纵向位移较小，因此在纵向地震输入下可不考虑横向位移。综上所述，行波效应对斜拉桥塔顶纵向位移峰值在软土区有显著影响，行波效应对塔顶纵向位移峰值影响的有利与否与地震波频谱特性有关[16]。

3.2.2视波速对主梁跨中位移的影响

图8为主梁跨中位移与视波速的关系曲线。由图8可见，行波效应对主梁跨中纵向位移峰值的影响规律与主塔纵向位移的影响规律相似。在软土区，汶川波和天津波的最小影响系数分别为0.29和0.89，El Centro波的最大影响系数为3.23；在岩石区，塔顶纵向位移峰值接近于一致激励的位移峰值。

一致激励下斜拉桥主梁跨中的竖向位移为0，考虑行波效应后斜拉桥主梁跨中产生了竖向位移，且在软土区，El Centro波作用下主梁跨中竖向位移峰值最大值达到28.4 cm，可见行波效应对主梁跨中竖向位移的影响不容忽视。综上所述，行波效应对斜拉桥主梁跨中纵向和竖向位移有较大的影响，当结构位于软土区时这种影响更加显著。

3.2.3视波速对塔底内力的影响

行波效应对斜拉桥塔底内力峰值的影响在软土区及其附近存在波动性，并不是单调变化，在岩石区逐渐趋于稳定（图9）。结构位于软土区时，在天津波、汶川波和El Centro波作用下行波效应对纵向剪力的增大效应并不显著，纵向剪力最小影响系数分别为0.75，0.86和0.77；塔底纵向弯矩峰值的影响系数变化范围分别为0.87～1.18，0.68～1.01，0.76～1.40；塔底轴力峰值的影响系数变化范围分别为0.78～1.24，1.22～1.75，1.11～1.53。在岩石区，3条地震波均增大左塔内力，减小右塔内力，其中天津波的影响最大，左塔塔底纵向剪力、纵向弯矩和轴力的最大影响系数分别为1.02，1.13，1.30，右塔塔底的最小影响系数分别为0.87，0.90，0.72。

可见，总体上行波效应可减小斜拉桥的塔底纵向剪力，且软土区对塔底纵向剪力的减小效应较为显著。行波效应在软土区和岩石区都会增大塔底的纵向弯矩和轴力，因此塔底内力需要考虑行波效应的影响。

3.2.4视波速对主梁跨中内力的影响

4结语

（1）行波效应对斜拉桥在地震作用下的位移和内力有显著的影响，这与地震波的传播速度有很大关系，相同地震波不同视波速作用下斜拉桥地震响应显著不同。不同地震波作用下所得的结果存在差异，不能笼统地定论行波效应对斜拉桥的抗震有利与否，要根据局部场地特征选定合适的地震波和视波速区间进行具体分析。

（2）在软土区（视波速50～250 m·s-1），行波效应对大跨度斜拉桥的位移和内力都有较大的影响，在进行斜拉桥设计时应予以考虑。

（3）在软土岩石过渡区（视波速250～2 000 m·s-1），行波效应会增大斜拉桥的跨中竖向位移、塔底和主梁的内力，在进行斜拉桥设计时可不考虑塔顶和跨中纵向位移的影响。

（4）在岩石区（视波速2 000～2 500 m·s-1），行波效应对大跨度斜拉桥的位移影响较小，但会产生较大的内力，在进行斜拉桥设计时不可忽视。

（5）应该指出的是，本文所采用的地震波数量有限，上述结论具有一定的局限性。基于所选的3种地震波得到的结论其普遍适用性还有待于考察更多的地震动记录以及更多复杂结构的地震响应加以验证。

参考文献：

References：

[1]HOUSNER G W.Characteristics of Strongmotion Earthquakes[J].Bulletin of the Seismological Society of America，1947，37（1）：1931.

[2]BONGDANOFF J L，GOLDENBERG J E，SCHIFF A E.The Effect of Ground Transmission Time on the图9塔底内力峰值对比

Fig.9Comparisons of Peak Internal Forces of Tower Bottom图10主梁跨中内力峰值对比

Fig.10Comparisons of Peak Internal Forces of Main Girder MidspanResponse of Long Structures[J].Bulletin of the Seismological Society of America，1965，55（3）：627640.

[3]PANDEY A D，KRISHNA P，SETHIA M R.Seismic Response Analysis of Cablestayed Bridges[C]//IAEE.Proceedings of the Seventh World Conference on Earthquake Engineering：Vol.Ⅷ.Istanbul：IAEE，1980：343350.

[4]项海帆.斜张桥在行波作用下的地震反应分析[J].同济大学学报，1983，11（2）：19.

XIANG Haifan.Earthquake Response Analysis of Cablestayed Bridges Under the Action of Travelling Waves[J].Journal of Tongji University，1983，11（2）：19.

[5]NAZMY A S，ABDELGHAFFAR A M.Effects of Ground Motion Spatial Variability on the Response of Cablestayed Bridges[J].Earthquake Engineering & Structural Dynamics，1992，21（1）：120.

[6]武芳文，薛成凤，赵雷.超大跨度斜拉桥考虑行波效应的地震动随机响应研究[J].地震学报，2010，32（2）：193202.

WU Fangwen，XUE Chengfeng，ZHAO Lei.Stochastic Seismic Response of Superlongspan Cablestayed Bridges Under Excitation of Traveling Waves[J].Acta Seismologica Sinica，2010，32（2）：193202.

[7]SOYLUK K，DUMANOGLU A A.The Effects of Local Soil Conditions and Wave Velocities to the Stochastic Response of Cablestayed Bridges[C]//ECAS.ECAS2002 International Symposium on Structural and Earthquake Engineering.Ankara：ECAS，2002：134141.

[8]许莉，郑旭霞.非一致地震激励下大跨斜拉桥的地震反应[J].福州大学学报：自然科学版，2013，41（4）：528533.

XU Li，ZHENG Xuxia.Seismic Response of Longspan Cable Stayed Bridge Under Asynchronous Excitations[J].Journal of Fuzhou University：Natural Science Edition，2013，41（4）：528533.

[9]陈幼平，周宏业.斜拉桥地震反应的行波效应[J].土木工程学报，1996，29（6）：6168.

CHEN Youping，ZHOU Hongye.Seismic Behavior of Cablestayed Bridges Under Travelling Wave Excitation[J].China Civil Engineering Journal，1996，29（6）：6168.

[10]克拉夫 R W，彭津 J.结构动力学[M].王光远，译.北京：科学出版社，1981.

CLOUGH R W，PENZIEN J.Dynamics of Structure[M].Translated by WANG Gangyuan.Beijing：Science Press，1981.

[11]肖帕 A K.结构动力学：理论及其在地震工程中的应用[M].谢礼立，吕大刚，译.2版.北京：高等教育出版社，2007.

CHOPRA A K.Dynamics of Structures：Theory and Applications to Earthquake Engineering[M].Translated by XIE Lili，LU Dagang.2nd ed.Beijing：Higher Education Press，2007.

[12]何庆祥，沈祖炎.结构地震行波效应分析综述[J].地震工程与工程振动，2009，29（1）：5057.

HE Qingxiang，SHEN Zuyan.Review of Structural Seismic Analysis of Travelling Wave Effects[J].Journal of Earthquake Engineering and Engineering Vibration，2009，29（1）：5057.

[13]林均岐，白春旭，陈永盛，等.多点激励下大跨度斜拉桥地震反应分析[J].地震工程与工程振动，2009，29（6）：154161.

LIN Junqi，BAI Chunxu，CHEN Yongsheng，et al.Study on the Seismic Response of Cablestayed Bridges with Multisupport Excitations[J].Journal of Earthquake Engineering and Engineering Vibration，2009，29（6）：154161.

[14]范立础，王君杰，陈玮.非一致地震激励下大跨度斜拉桥的响应特征[J].计算力学学报，2001，18（3）：358363.

FAN Lichu，WANG Junjie，CHEN Wei.Response Characteristics of Longspan Cablestayed Bridges Under Nonuniform Seismic Action[J].Chinese Journal of Computational Mechanics，2001，18（3）：358363.

[15]周国良，李小军，刘必灯，等.大刚度法在结构动力分析中的应用、误差分析与改进[J].工程力学，2011，28（8）：3036，44.

ZHOU Guoliang，LI Xiaojun，LIU Bideng，et al.Error Analysis and Improvements of Large Spring/Stiffness Method for Structural Dynamic Response Analysis[J].Engineering Mechanics，2011，28（8）：3036，44.

[16]周国良，李小军，刘必灯，等.大质量法在多点激励分析中的应用、误差分析与改进[J].工程力学，2011，28（1）：4854.

ZHOU Guoliang，LI Xiaojun，LIU Bideng，et al.Error Analysis and Improvements of Large Mass Method Used in Multisupport Seismic Excitation Analysis[J].Engineering Mechanics，2011，28（1）：4854.

[17]BOZORGNIA Y，CAMPBELL K W.Vertical Ground Motion Model for PGA，PGV，and Linear Response Spectra Using the NGAWest2 Database[J].Earthquake Spectra，2016，32（2）：9791004.

[18]SOYLUK K，SICACIK E A.Soilstructure Interaction Analysis of Cablestayed Bridges for Spatially Varying Ground Motion Components[J].Soil Dynamics and Earthquake Engineering，2012，35：8090.

[19]BI K，HAO H，CHOUW N.Influence of Ground Motion Spatial Variation，Site Condition and SSI on the Required Separation Distances of Bridge Structures to Avoid Seismic Pounding[J].Earthquake Engineering & Structural Dynamics，2011，40（9）：10271043.

[20]张喜刚，陈艾荣.千米级斜拉桥——结构体系、性能与设计[M].北京：人民交通出版社，2010.

ZHANG Xigang，CHEN Airong.Kilometerscale Cable Stayed Bridge — Structural System，Performance and Design[M].Beijing：China Communications Press，2010.