基于简化修正压力场理论的钢筋混凝土柱荷载变形分析

仇建磊+贡金鑫

摘要：基于简化修正压力场理论对钢筋混凝土柱抗剪机理进行了分析，并考虑核心混凝土膨胀对箍筋抗剪承载力贡献的影响，计算了骨料咬合作用及受压区的抗剪承载力贡献，获得受拉区和受压区的抗剪强度，从而建立箍筋屈服后柱构件抗剪强度计算方法；结合传统截面纤维分析法，同时引入弯曲变形、剪切变形及滑移变形3种变形分量，在箍筋屈服前对柱构件进行抗弯分析，最终得出压弯剪作用下钢筋混凝土柱荷载变形曲线，并与所收集的15个钢筋混凝土柱低周反复试验结果进行了对比。研究结果表明：采用该方法计算的荷载变形曲线与试验骨架曲线吻合较好，对发生弯曲破坏、弯剪破坏及剪切破坏3种不同破坏类型的钢筋混凝土柱均有较好的分析效果，可用于压弯剪作用下钢筋混凝土柱的荷载变形分析。

关键词：钢筋混凝土柱；荷载变形；修正压力场理论；骨架曲线

中图分类号：TU375.3文献标志码：A

Abstract： The shear mechanism of reinforced concrete columns was analyzed based on simplified modified compression field theory. Considering the effect of expansion of core concrete on the shear capacity contribution of stirrups， the shear capacity contribution of aggregate interlock behavior and compressive zone were calculated. The shear strengths of tensile area and compressive area were obtained， and the calculation method of shear strength of column after stirrups yielded was established. Combined with the conventional section fiber analysis method， while three deformation components of bending deformation， shear deformation and slip deformation were introduced， the bending analysis of columns before stirrups yielded was carried out， the loaddeformation curves of reinforced concrete columns under compression bending shear action were obtained， and compared with the low cycle test results of 15 reinforced concrete columns collected. The results show that the loaddeformation curves calculated by the proposed method agree well with the test loaddeformation skeleton curves， and have better analysis effect on the reinforced concrete columns with flexural failure， bending shear failure and shear failure. The proposed method can be used for loaddeformation analysis of reinforced concrete columns under compression bending shear action.

Key words： reinforced concrete column； loaddeformation； modified compression field theory； skeleton curve

0引言

钢筋混凝土柱作为钢筋混凝土框架结构和桥梁结构中的主要承重及抗侧力构件，其抗震性能的优劣对整体结构有着重要影响。根据钢筋混凝土柱在地震作用下的破坏特征，其破坏模式可分为弯曲破坏、弯剪破坏以及剪切破坏3种，其中发生弯曲破坏的钢筋混凝土柱延性发展充分，具备良好的耗能机制，在地震中的危害相对较小，可以满足结构抗震延性设计要求。以剪切起控制作用的剪切破坏及弯剪破坏具有明显的脆性特征，设计中应予以避免。大量震后调查发现[12]，强烈地震作用下，钢筋混凝土柱容易发生柱端剪切破坏，主要原因是箍筋配置不足，出现塑性铰后柱端抗剪承载力难以抵抗水平剪力。除此之外，窗间墙的不合理设置及错层结构均容易形成短柱结构形式，同样会造成其在地震作用下发生剪切破坏。实际上，随着中国抗震规范不断发展更新，抗震设计体系得到逐步完善，尤其是《建筑抗震设计规范》（GB 50011—2010）的颁布，增加了有关实现抗震性能设计目标的参考方法，但现役的建筑及桥梁结构中仍有不少是按旧规范设计的，其抗震性能评估亟待进行。因此，有必要对不同破坏模式的钢筋混凝土柱抗震性能进行研究，为结构抗震设计及评估提供依据。

轴向荷载和水平荷载共同作用下的钢筋混凝土柱的荷载变形关系可在一定程度上反映其抗震性能，包括抗剪承载力的大小及变形能力的强弱等。在对钢筋混凝土结构进行弹塑性时程分析时，需要先建立其构件恢复力模型，其主要由骨架曲线及滞回规则两部分组成，前者一般可通过单调加载荷载变形曲线计算获得。对于弯曲破坏模式下的钢筋混凝土柱，其剪切作用不明显，采用传统截面纤维分析法就能获得较好的分析结果，而对于弯剪破坏和剪切破坏构件，简单地采用截面纤维分析法不能对剪切作用进行分析，计算结果误差较大。

针对考虑剪切作用影响的钢筋混凝土柱荷载变形曲线计算方法，各国学者已经进行了为数不少的相关研究[38]。Mostafaei等[34]在经典修正压力场理论基础上建立了压弯剪相互作用下钢筋混凝土柱荷载变形曲线计算方法，其中柱构件剪切特性采用修正压力场进行描述，弯曲特性采用截面纤维分析法进行描述，但计算过程较为复杂，涉及大量迭代分析过程；Setzler等[5]按照弯曲作用和剪切作用主导程度对钢筋混凝土柱构件受力情况进行分类并计算，得到了相对简单的荷载变形计算方法，但对于弯剪相互作用并未进行深入考虑；魏巍巍等[6]在经典修正压力场理论基础上考虑了受压区混凝土抗剪承载力，建立了荷载变形计算模型，计算过程较为复杂；张勤等[7]采用经验修正方法对弯剪破坏钢筋混凝土柱荷载变形进行了研究，蔡茂等[8]利用多弹簧模型得到剪力剪切位移关系，建立了考虑剪切作用的柱荷载变形计算方法。上述方法均对剪切作用进行了考虑，但其计算过程较为复杂，或对弯剪相互作用考虑不足，为此本文建立一种更为简便的计算方法，即考虑弯剪相互作用对钢筋混凝土柱荷载变形曲线进行计算。

简化修正压力场理论是在经典修正压力场理论基础上发展得来的，由Collins等[9]于1996年首次提出，2006年Bentz等[10]对其进行了修正，该方法简化了传统修正压力场理论计算流程，避免了复杂的迭代过程，便于工程应用，加拿大、美国、欧洲相关规范中抗剪设计均以该方法为理论基础[1114]。实际上，简化修正压力场理论仅适用于混凝土开裂区的抗剪强度计算，而忽略了混凝土受压区的抗剪贡献，对于压弯剪共同作用下的钢筋混凝土柱，难以进行荷载变形全过程分析。此外，在钢筋混凝土柱受力过程中，核心混凝土膨胀对箍筋应力影响较大，其部分应力用于为核心混凝土提供约束作用，为此本文在对箍筋抗剪承载力贡献计算中考虑了核心混凝土膨胀的影响，基于简化修正压力场理论对受拉区抗剪承载力进行了计算，同时考虑了受压区混凝土抗剪贡献，结合截面纤维分析法获得压弯剪作用下的钢筋混凝土柱荷载变形曲线，最后与所收集的试验结果进行了对比。

1钢筋混凝土柱抗剪分析

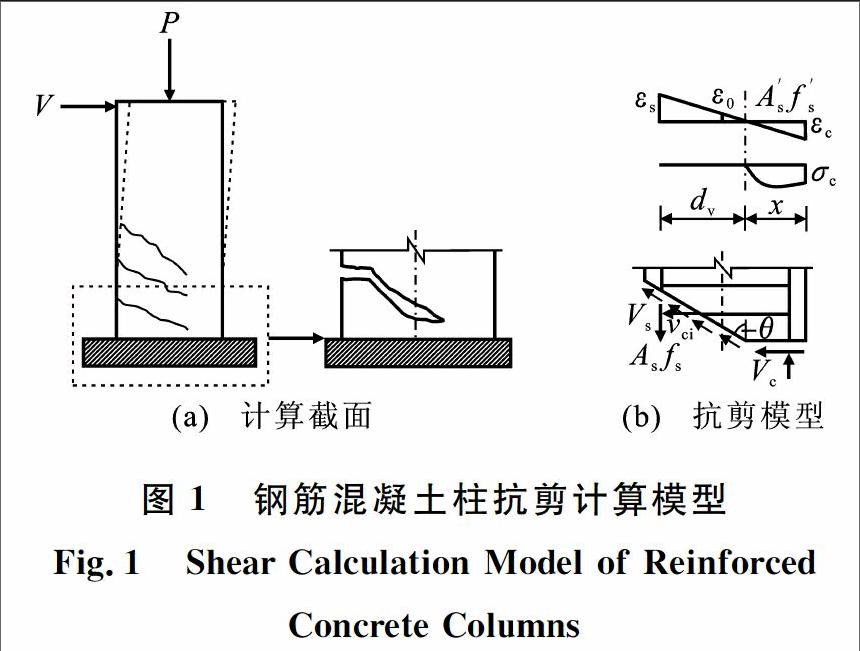
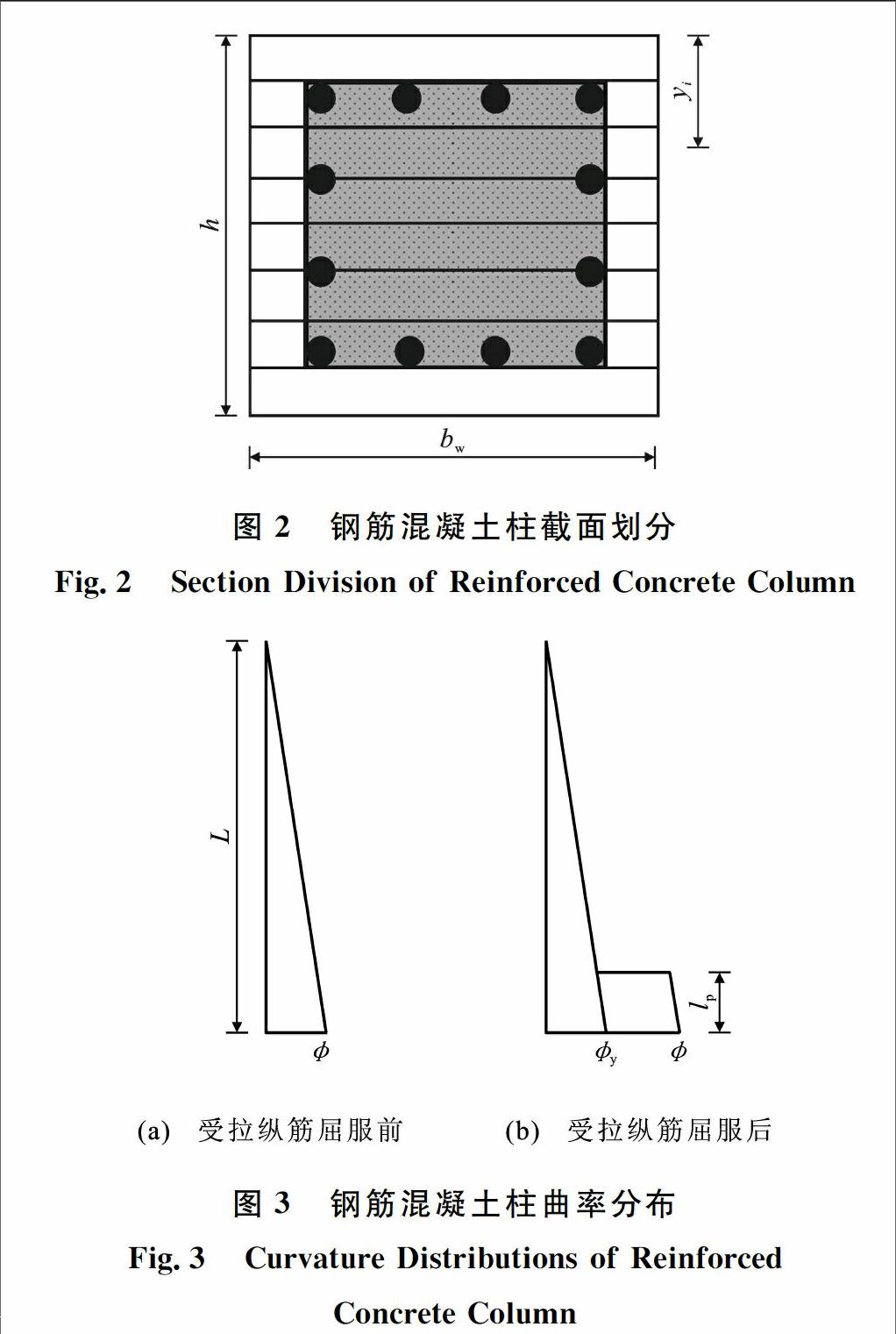
本文将建立适用于弯曲、弯剪及剪切破坏3种不同破坏模式的钢筋混凝土柱荷载变形分析方法。上述钢筋混凝土柱抗剪分析中箍筋应力采用的是箍筋屈服强度，可以对箍筋屈服后的抗剪承载力进行计算，但对于箍筋屈服之前或箍筋不屈服的情况难以进行适当的分析。鉴于此，本文采用传统截面纤维分析法对箍筋屈服之前及箍筋不屈服的情况进行分析，此时将按照弯曲理论对钢筋混凝土柱进行计算分析，其截面划分如图2所示（图2中，yi为第i个条带中心距受压边缘距离），建立计算截面分析模型，得出弯矩曲率关系，并根据塑性铰模型（图3）计算荷载变形曲线。图3中，为截面曲率，y为受拉纵筋屈服时截面曲率，lp为塑性铰长度。

2.5荷载变形分析步骤

根据本文已经建立的钢筋混凝土柱箍筋屈服后抗剪承载力计算方法及引入变形分量的传统截面纤维分析法，可对钢筋混凝土柱荷载变形曲线进行全过程分析，具体计算步骤如下：

（1）给定截面初始曲率0，已知轴向荷载P，根据式（9），（10）迭代计算截面中间应变ε0，由式（11）计算截面弯矩。

（2）逐步增大截面曲率，并建立截面弯矩曲率关系。

（3）按式（12），（26）计算得出弯曲分析条件下的水平荷载V′及侧向变形Δ。

（4）按式（1）计算箍筋屈服后钢筋混凝柱抗剪承载力V。

（5）对比V′和V，当V′≥V时，即认为箍筋已经屈服，按剪切作用控制，水平荷载取V，并根据V修正剪切变形Δv，进而得到相应侧向变形Δ。

（6）由已经计算得到的水平荷载和侧向变形，建立钢筋混凝土柱荷载变形关系。

3计算结果与试验结果对比

为验证本文建议计算方法的合理性，收集了15个钢筋混凝土柱低周反复试验数据（表1），构件破坏类型包括弯曲破坏、弯剪破坏及剪切破坏3种类型，柱剪跨比为1.5～4.0，轴压比为0.07～0.62，配箍率为0.068%～1.13%，纵筋配筋率为1.51%～3.03%，混凝土抗压强度为21.1～46.5 MPa。

图8为按本文计算方法得到的单调荷载变形曲线与试验骨架曲线的对比结果，其中，图8（a）～（d）为弯曲破坏，图8（e）～（m）为弯剪破坏，图8（n），（o）为剪切破坏。由图8可知，忽略循环加载制度的影响，按本文计算方法能够对弯曲、弯剪、剪切破坏构件的荷载变形曲线进行较好预测。对于弯剪、剪切破坏情况，构件在达到剪切破坏点后承载力开始显著下降，计算荷载变形曲线能够对其剪切破坏点进行较为准确的预测，承载力下降段吻合较好，能够得到各构件的极限位移。对于弯曲破坏构件，本文通过计算给出其水平承载力下降至0的曲线，通过对比发现，能够准确计算其屈服位移、水平承载力及破坏点。

选取弯曲破坏构件No.3、弯剪破坏构件2CLH18、剪切破坏构件3CMD12的箍筋应力fsv进行分析，结果如图9所示。对于上述3种破坏模式，由核心混凝土膨胀引起的箍筋拉应力均呈不断增加趋势，用于箍筋抗剪的组成则随之下降，需要说明的是，图9所示为箍筋屈服后应力分析。此外，对于弯曲破坏构件，其箍筋抗剪贡献下降速度最慢，剪切破坏构件最快，弯剪破坏构件位于两者之间。实际上，对于弯曲破坏构件，由于剪切作用影响不大，其截面受力以受弯为主，因此箍筋抗剪贡献随位移增加下降趋势不够明显。相比之下，弯剪、剪切破坏构件主要以剪切作用控制其破坏，箍筋抗剪作用对构件影响较大，因此其随位移增长下降趋势较为明显。4结语

（1）本文基于简化修正压力场理论对压弯钢筋混凝土柱构件进行了抗剪分析，并进一步考虑了核心混凝土膨胀对箍筋抗剪贡献影响以及受压混凝土的抗剪承载力贡献，结合传统截面纤维分析法对钢筋混凝土柱进行了分析，最终得出能够考虑剪切作用影响的钢筋混凝土柱荷载变形曲线计算方法。

（2）通过与试验骨架曲线进行对比可知，本文方法计算的钢筋混凝土柱荷载变形曲线与试验曲线吻合较好，同时适用于弯曲、弯剪及剪切3种破坏类型的钢筋混凝土柱分析。与以往方法相比，本文方法避免了复杂的迭代计算过程，且力学分析模型清晰，具备一定理论依据，可用于钢筋混凝土柱荷载变形性能分析。

参考文献：

References：

[1]霍林生，李宏男，肖诗云，等.汶川地震钢筋混凝土框架结构震害调查与启示[J].大连理工大学学报，2009，49（5）：718723.

HUO Linsheng，LI Hongnan，XIAO Shiyun，et al.Earthquake Damage Investigation and Analysis of Reinforced Concrete Frame Structures in Wenchuan Earthquake[J].Journal of Dalian University of Technology，2009，49（5）：718723.

[2]贡金鑫，王雪婷，张勤.从汶川地震灾害看现行国内外桥梁抗震设计方法[J].大连理工大学学报，2009，49（5）：739747.

GONG Jinxin，WANG Xueting，ZHANG Qin.Overview on Current Bridge Seismic Design Approach in图8计算荷载变形曲线与试验曲线的对比

Fig.8Comparisons of Calculated Loaddeformation Curves and Experiment Curves图9箍筋应力分析结果

Fig.9Stress Analysis Results of StirrupsHome and Abroad Codes Based on Survey of Wenchuan Earthquake[J].Journal of Dalian University of Technology，2009，49（5）：739747.

[3]MOSTAFAEI H，KABEYASAWA T.Axialshearflexure Interaction Approach for Reinforced Concrete Columns[J].ACI Structural Journal，2007，104（2）：218226.

[4]MOSTAFAEI H，VECCHIO F J.Uniaxial Shearflexure Model for Reinforced Concrete Elements[J].Journal of Structural Engineering，2008，134（9）：15381547.

[5]SETZLER E J，SEZEN H.Model for the Lateral Behavior of Reinforced Concrete Columns Including Shear Deformations[J].Earthquake Spectra，2008，24（2）：493511.

[6]魏巍巍，贡金鑫.钢筋混凝土柱荷载变形计算的理论模型[J].建筑科学与工程学报，2012，29（1）：3849.

WEI Weiwei，GONG Jinxin.Theoretical Models of Loaddeformation Calculation for Reinforced Concrete Columns[J].Journal of Architecture and Civil Engineering，2012，29（1）：3849.

[7]张勤，贡金鑫.弯剪破坏钢筋混凝土柱的荷载变形关系[J].建筑科学与工程学报，2010，27（3）：7884.

ZHANG Qin，GONG Jinxin.Loaddeformation Relations of Reinforced Concrete Columns Under Flexuralshear Failure[J].Journal of Architecture and Civil Engineering，2010，27（3）：7884.

[8]蔡茂，顾祥林，华晶晶，等.考虑剪切作用的钢筋混凝土柱地震反应分析[J].建筑结构学报，2011，32（11）：97108.

CAI Mao，GU Xianglin，HUA Jingjing，et al.Seismic Response Analysis of Reinforced Concrete Columns Considering Shear Effects[J].Journal of Building Structures，2011，32（11）：97108.

[9]COLLINS M P，MITCHELL D，ADEBAR P，et al.A General Shear Design Method[J].ACI Structural Journal，1996，93（1）：3645.

[10]BENTZ E C，VECCHIO F J，COLLINS M P.Simplified Modified Compression Field Theory for Calculating Shear Strength of Reinforced Concrete Elements[J].ACI Structural Journal，2006，103（4）：614624.

[11]CSA A23.304，Design of Concrete Structures[S].

[12]CAN/CSAS600，Canadian Highway Bridge Design Code[S].

[13]AASHTO，LRFD Bridge Design Specifications[S].

[14]CEBFIP，Fib Model Code for Concrete Structures 2010[S].

[15]贡金鑫，魏巍巍，赵尚传.现代混凝土结构基本理论及应用[M].北京：中国建筑工业出版社，2009.

GONG Jinxin，WEI Weiwei，ZHAO Shangchuan.Fundamental Theory and Application of Modern Reinforced Concrete Structures[M].Beijing：China Architecture & Building Press，2009.

[16]ESMAEILYGH A，XIAO Y.Seismic Behavior of Bridge Columns Subjected to Various Loading Patterns[R].Berkeley：PEER，2002.

[17]MANDER J B，PRIESTLEY M J N，PARK R.Theoretical Stressstrain Model for Confined Concrete[J].Journal of Structural Engineering，1988，114（8）：18041826.

[18]SAATCIOGLU M，RAZVI S R.Strength and Ductility of Confined Concrete[J].Journal of Structural Engineering，1992，118（6）：15901607.

[19]ANG B G.Ductility of Reinforced Concrete Bridge Piers Under Seismic Loading[D].Christchurch：University of Canterbury，1981.

[20]SOESIANAWATI M T.Limited Ductility Design of Reinforced Concrete Columns[D].Christchurch：University of Canterbury，1986.

[21]OHUE M，MORIMOTO H，FUJII S，et al.Behavior of R.C.Short Columns Failing in Splitting Bondshear Under Dynamic Lateral Loading[J].Transactions of the Japan Concrete Institute，1985，7：293300.

[22]ONO A，SHIRAI N，ADACHI H，et al.Elastoplastic Behavior of Reinforced Concrete Column with Fluctuating Axial Force[J].Transactions of the Japan Concrete Institute，1989，11：239246.

[23]LYNN A C.Seismic Evaluation of Existing Reinforced Concrete Building Columns[D].Berkeley：University of California，2001.

[24]SEZEN H.Seismic Behavior and Modeling of Reinforced Concrete Building Columns[D].Berkeley：University of California，2002.

[25]PRIESTLEY M J N，SEIBLE F，CALVI G M.Seismic Design and Retrofit of Bridges[M].New York：John Wiley & Sons，1996.

[26]SEZEN H，SETZLER E J.Reinforcement Slip in Reinforced Concrete Columns[J].ACI Structural Journal，2008，105（3）：280289.

[27]PUJOL S.Drift Capacity of Reinforced Concrete Columns Subjected to Displacement Reversals[D].West Lafayette：Purdue University，2002.