不确定条件下集成风险缓解策略的可靠供应链网络设计

王海燕　季　苗

(福州大学经济与管理学院， 福建福州　350116)



不确定条件下集成风险缓解策略的可靠供应链网络设计

王海燕季苗

(福州大学经济与管理学院， 福建福州350116)

摘要：针对供应链网络设计面临的需求波动和设施节点中断两类不确定因素，利用鲁棒优化方法处理需求的不确定性，采用情景的方法描述配送中心的中断及能力损失情况，提出对不可靠的设施进行投资设防和在可靠的设施处预留部分冗余能力两种防御保护措施，并将其嵌入模型，分别建立以期望成本为目标的多周期、多情景两阶段随机规划模型和以名义成本为目标的p鲁棒优化模型，以确定配送中心选址、防御措施选择、客户分配、可靠配送中心的冗余配送能力以及设施之间的物流量，最后通过算例验证模型的有效性和可行性。

关键词：供应链网络设计; 需求不确定; 中断风险; 风险缓解策略; 两阶段随机优化

引言

在现今这个全球化开放的市场，企业与企业之间的竞争越来越依赖其供应链的竞争，一个可靠且又健壮的供应链网络无疑会给企业带来持续的竞争优势。然而，供应链网络设计面临诸多不确定性因素，常见的两类不确定因素包括输入参数的不确定性和设施节点的中断风险。不确定性的存在意味着供应链网络设计面临一定的风险，而正是这些潜在的风险增加了供应链网络设计的难度与复杂性。因此，风险环境下的可靠供应链网络设计成为企业亟需解决的问题。

目前，不确定环境下的供应链网络设计研究已有许多。大部分研究将这两类不确定性因素分开考虑。Pishvaee、Ramezani等考虑需求、回收数量等输入参数的不确定性，并利用鲁棒优化方法研究了闭环供应链网络的设计问题。[1][2]刘希龙等学者研究了供应端面临中断风险的供应链网络设计问题，提供了许多缓解供应端中断风险的应急策略，如对供应商进行投资保护、建立期权契约、采取多源供应、预留应急库存等等。[3][4][5][6][7][8][9][10]然而考虑中间节点中断[11][12][13][14][15]的供应链网络设计研究相对较少。Azad研究了配送中心和运输连接同时面临失效风险的两级配送网络的设计问题，提出对不可靠配送中心进行投资加固和转运两种防御措施，用概率描述不可靠配送中心和运输连接的失效，建立了单周期混合整数规划模型。[16]Hatefi运用Bertsimas和Sim介绍的鲁棒优化方法处理需求、回收数量及废弃率等不确定性参数，同时采用情景的方法描述设施的中断情况，建立了带有p鲁棒约束的单周期混合整数规划模型。[17]Hatefi运用模糊数学方法处理输入参数的不确定性，建立了带有置信度约束的单周期混合整数线性规划模型，以解决前逆向集成网络节点的选址和最优流量分配问题。[18]

本文设计出一个三级配送网络，在同时考虑需求和设施中断的基础上集成Azad和Hatefi的风险缓解策略[19][20]，提出在配送中心预留一部分应急配送能力，转运量必须小于该应急储备能力。其次，像自然灾害比如洪水、冰雹等中断事件的发生具有明显的季节特点，不同时期设施面临的中断事件也不相同，基于情景的多周期随机规划模型更适合实际网络规划的需要。因此，本文在集成考虑组合风险缓解策略的基础上，同时考虑需求不确定性和设施中断风险，建立了多周期、多情景的两阶段随机规划模型，以确定配送中心的选址、防御措施的选择、客户分配、可靠配送中心的冗余配送能力以及设施之间物流量。

一、问题描述及假设

本文设计的三级配送网络，包括一个制造商、多个配送中心和多个客户。制造商根据市场需求采用准时制生产方式组织生产，通过配送中心运至客户，市场需求是不确定的。考虑到备选配送中心地域的分散性，部分配送中心暴露在风险环境中，存在失效风险，且设施面临的中断事件不同，各期中断情况又不同，中断后仍有部分能力剩余；而另外一部分设施相对可靠，不会受到中断事件的影响。针对此种情况，本文提出两种防御措施缓解设施中断的风险。第一，对不可靠配送中心进行投资设防，投资设防水平越高，保护力度越大，设施受到冲击后损失的配送能力越少；第二，在可靠配送中心预留一部分配送能力，只有当不可靠配送中心受到冲击后才能从可靠的配送中心调运这部分能力。决策内容包括配送中心的选址、防御措施的选择、客户分配、各期可靠配送中心预留的冗余配送能力以及设施之间的物流量。

模型假设：(1)两类配送中心均在一定备选地点范围选择，且配送能力已知；(2)中断事件对配送能力的影响仅限当期，下期恢复正常水平；(3)不考虑制造商和配送中心的库存；(4)不考虑不可靠配送中心之间的转运；(5)中断事件主要对不可靠配送中心的配送能力产生影响。

二、模型的建立

1. 数学符号及含义说明

(1)集合说明：K：客户集合，k∈K；AU：不可靠配送中心备选地点集合，j∈AU；AR：可靠配送中心备选地点集合，j′∈AR；N：投资加固水平集合，n∈N ；T：生产规划周期集合，t∈T；S：配送中心状态情景集合，s∈S。

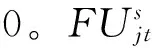
2. 基础模型

考虑到不可靠配送中心出现的失效情景，本文的可靠供应链网络设计可看作是一个两阶段决策问题。第一阶段是指在设施节点中断未发生前，确定配送中心的选址、不可靠配送中心的投资加固等级及客户分配、战略应急储备配送能力；第二阶段指不可靠配送中心发生中断后，在第一阶段决策的基础上确定各情景下设施之间的物流量及转运量。整个决策过程以期望成本最小为目标，建立的多周期、多情景两阶段随机规划模型如下：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

其中：目标函数是所有情景下的期望成本最小。式(1)保证可靠的配送中心至少有一个；式(2)表示任意一个不可靠配送中心投资水平最多只有一种；式(3)保证每一个客户只能分配给一个配送中心；式(4)～(5)保证制造商将产品运至开放的配送中心；式(6)～(7)保证只有当客户分配给某一配送中心时，客户与该配送中心才存在物流量；式(8)～(9)保证客户分配给开放的配送中心；式(10)～(12)描述战略应急配送能力的使用条件；式(13)～(14)保证客户需求全部满足，其中需求的不确定性利用Ben-tal和Nemirovski提出的鲁棒优化方法处理，具体应用步骤参考Pishvaee的研究结果[21]；式(15)～(16)表示配送中心的能力约束；式(17)～(18)表示流入配送中心的物流量等于流出的物流量；式(19)表示变量约束。

3. p鲁棒优化模型

以名义成本(没有发生中断情景下的成本)为目标函数，本文中将情景1设为无中断发生的情景，建立如下p鲁棒优化模型：

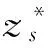
该情景s满足约束(1)～(19)。

P(Ⅰ)和P(Ⅱ)两个模型优化目标不相同，保守型决策者期望优化所有情景下的平均成本，模型P(Ⅰ)更加合适；而有些决策者着眼于名义情景下的成本，毕竟中断情景发生的概率甚小，同时希望控制不同情景下成本的波动范围，此时选择P(Ⅱ)更加合适。

三、算例及分析

以某制造企业为例，该企业考虑从5个备选配送中心(2个可靠配送中心和3个不可靠配送中心)中确定其最佳的位置及数量，同时选择合适的风险缓解策略以应对设施中断和需求波动带来的风险。该制造商生产规划期有3个，生产单一产品，共有6个客户。投资加固等级分别用0,1,2,3表示，0表示不考虑投资加固，1,2,3分别表示低、中、高三类投资加固水平。假设不可靠配送中心状态情景共8种，情景1表示无中断发生，情景2～7分别描述不同周期设施的中断情况，见表1，各情景发生概率见表2(限于篇幅其他参数未提供)。模型可通过GAMS/CPLEX、lingo等优化软件求解。

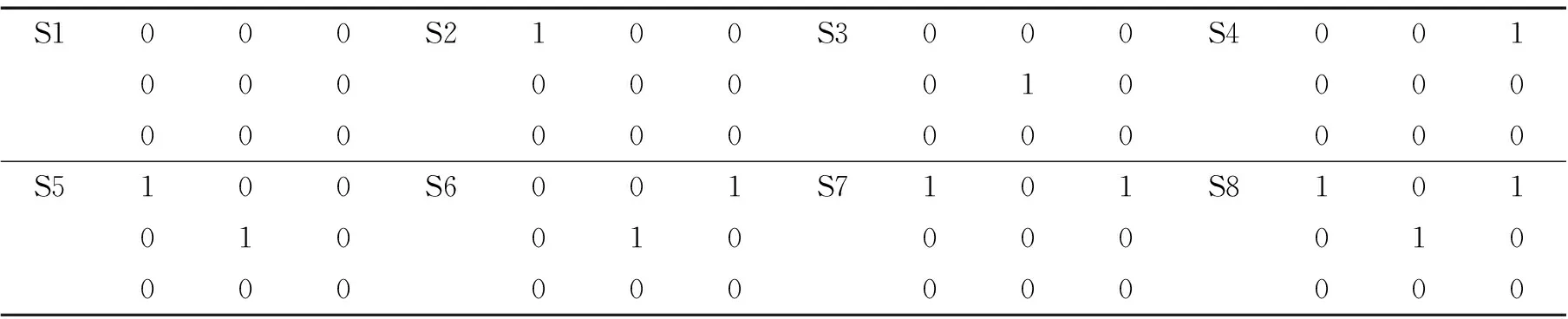
表1　不可靠配送中心各期状态情景

表2　各情景发生概率

1. 需求不确定性参数变化对模型结果的影响

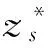
表3　不同ρt、Gkt下P(Ⅰ)和P(Ⅱ)的目标函数值

表4　不同ρt、Gkt下P(Ⅰ)和P(Ⅱ)的设施开放及客户分配情况

注：R1表示可靠配送中心1，UR1表示不可靠配送中心1，UR1(低)表示不可靠配送中心1的投资设防水平为低水平。

由表3可知，在P(Ⅱ)中p值给定前提下，随着需求的波动程度增加，P(Ⅰ)、P(Ⅱ)的目标函数值均逐渐增加，与确定需求(ρt=0，Gkt=0)相比较，不确定需求情形下的成本均比确定需求情形下的成本高，因此决策者需要付出更多的成本以应对需求不确定带来的风险。表4中，当需求不确定性参数发生变化时，设施开放情况保持不变，但随着ρt和Gkt的逐渐提高，需求的波动程度越大，P(Ⅰ)、P(Ⅱ)优化结果下的网络结构及投资加固决策也会发生变化。值得注意的是当需求波动程度增强时，对不可靠设施投资加固的平均水平不一定提高，如ρt和Gkt取值由(0.2,200)向(0.5,300)变化时，对UR1的投资加固等级由中等降为低等，而UR2继续保持低水平投资；R1的客户分配由(1,2,3)变为(1,3,4)，UR1的客户分配由(4,5)变为(2,5)。

2. p值变化对模型P(Ⅱ)求解结果的影响

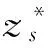
表6　未考虑p鲁棒约束的P(Ⅱ)求解结果下各情景的最优成本

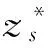
由表7、表8可知，随着p值增加，P(Ⅱ)的目标函数值保持不变，但P(Ⅱ)优化结果下各情景的平均遗憾值发生变化。p值越大，P(Ⅱ)的平均遗憾值未必越大，各情景下的遗憾值变化也未必越平稳。比如p值由0.3增加至0.5时，平均遗憾值变小，标准差变大。表8中，只有当p取0.06时，P(Ⅰ)各情景的平均遗憾值与P(Ⅱ)的基本相同；当p取其他值时，P(Ⅰ)所有情景下的平均遗憾值均比P(Ⅱ)的小。

表7　不同p值下P(Ⅱ)的目标函数值

表8　　　　P(Ⅰ)和P(Ⅱ)优化结果下所有情景的平均

四、结论

本文考虑了供应链网络设计面临的两类风险：需求波动和设施节点的中断，同时在模型中嵌入多种风险缓解策略，采用鲁棒优化方法处理需求的不确定性，利用情景的方法描述设施中断及其能力损失情况，分别建立多周期、多情景的两阶段随机优化模型和p鲁棒优化模型，并对相关参数进行灵敏性分析。结论表明，嵌入的组合风险缓解策略能有效抵御配送节点中断带来的风险；需求波动越大，决策者需要付出更多的成本以降低需求不确定的风险；p值越大，P(Ⅱ)的平均遗憾值未必越大，各情景下的遗憾值变化也未必越平稳。

注释：

[1][21] Pishvaee M. S.，Rabbani M.，Torabi S. A．，“A robust optimization approach to closed-loop supply chain network design under uncertainty”，AppliedMathematicalModelling，vol.35,no.2(2011),pp.637-649．

[2] Ramezani M.，Bashiri M.，“Tavakkoli-Moghaddam R．A new multi-objective stochastic model for a forward/reverse logistic network design with responsiveness and quality level”，AppliedMathematicalModelling，vol.37,no.1-2(2013)．

[3] 刘希龙、季建化：《基于多源供应的弹性供应网络研究》,《工业工程与管理》2007年第3期。

[4] 刘希龙、季建化：《基于应急供应的弹性供应网络设计研究》,《控制与决策》2007年第11期。

[5] Xu N. X.，Nozick L．,“Modeling supplier selection and the use of option contracts for global supply chain design”，Computers&OperationsResearch，vol.36,no.10(2009)，pp.2786-2800．

[6] Peng P.，Snyder L. V.，Lim A．,“Reliable logistics networks design with facility disruptions”，TransportationResearchPartB：Methodological，vol.45,no.8(2011)，pp.1190-1211．

[7] Li Q.，Zeng B.，Savachkin A．,“Reliable facility location design under disruptions”,Computers&OperationsResearch，vol.40,no.3(2013)，pp.901-909．

[8] Torabi S. A.，Baghersad M.，Mansouri S. A.,“Resilient supplier selection and order allocation under operational and disruption risks”，TransportationResearchPartE：LogisticsandTransportationReview，vol.79(2015)，pp.22-48．

[9] Mohammaddust F.，Rezapour S.，Farahani R. Z．,“Developing lean and responsive supply chains：A robust model for alternative risk mitigation strategies in supply chain designs”，InternationalJournalofProductionEconomics，http://dx.doi.org/10.1016/j.ijpe.2015.09.12．

[10] 陶 瑾、关志民、高 聪：《基于均值-风险模型的弹性供应网络集成优化》，《技术经济》2015年第7期。

[11][16][19] Azad N.，Davoudpour H.，Saharidis G. K. D., “A A new model to mitigating random disruption risks of facility and transportation in supply chain network design”，TheInternationalJournalofAdvancedManufacturingTechnology，vol.79,no.9-12(2013)，pp.1757-1774．

[12] 秦绪伟、喻海飞、黄小原：《有限能力物流系统防御设计随机模型及算法》，《东北大学学报》(自然科学版)2012年第6期。

[13] 陶 瑾、关志民：《基于决策者风险态度的弹性分销网络优化模型》，《经济管理》2015年第7期。

[14][17] Hatefi S. M.，Jolai F．,“Robust and reliable forward-reverse logistics network design under demand uncertainty and facility disruptions”,AppliedMathematicalModelling，vol.35,no.9-10(2014)，pp.2630-2647．

[15][18][20] Hatefi S. M.，Jolai F.，Torabi S. A.,“A credibility-constrained programming for reliable forward-reverse logistics network design under uncertainty and facility disruptions”，InternationalJournalofComputerIntegratedManufacturing,vol.28,no.6(2015)，pp.664-678．

[责任编辑：黄艳林]

收稿日期：2016-01-15

基金项目：福建省自然科学基金资助项目(2014J05082)

作者简介：王海燕， 女， 湖南衡阳人， 福州大学经济与管理学院副教授，博士；

中图分类号：F253.4

文献标识码：A

文章编号：1002-3321(2016)02-0039-06

季苗， 女， 湖北仙桃人， 福州大学经济与管理学院硕士研究生。